статья моделирование. Статья_Модели кольмотации пористых сред. Толеуов Тимур Жаксылыкович
 Скачать 53.08 Kb. Скачать 53.08 Kb.
|
|
Толеуов Тимур Жаксылыкович Актюбинский региональный университет имени К.Жубанова, актобе, Казахстан Магистр математики, PhD докторант Timur_Toleuov@mail.ru, +7-705-830-4855 Timur Zh.Toleuov Aktobe Regional University named after Kh.Zhubanov, Aktobe, Kazakhstan Master of Mathematics, PhD student Timur_Toleuov@mail.ru, +7-705-830-4855 Мухамбетжанов Салтанбек Талапеденович Казахский национальный университет имени Аль-Фараби, Алматы, Казахстан Доктор физико-математическиъ наук, профессор Mukhambetzhanov@mail.ru Saltanbek T. Mukhambetzhanov Al-Farabi Kazakh National University, Almaty, Kazakhstan Doctor of Physical and Mathematical Sciences, Professor Mukhambetzhanov@mail.ru Юлдашев Зиявутдин Хабибович Национальный университет Узбекистана имени Мирзо Улугбек, Ташкент, Узбекистан Доктор физико-математическиъ наук, профессор Ziyaut@mail.ru YuldashevKh. Ziyavidin Ulugbek National University of Uzbekistan, Tashkent, Uzbekistan Doctor of Physical and Mathematical Sciences, Professor Ziyaut@mail.ru Аннотация Закупорка пор пористой среды твердыми частицами (кольматация) и обратный процесс отрыва и переноса частиц вглубь пористой среды (суффозия) происходят и при первичном, и при вторичном вскрытии пластов. Процесс кольматации продуктивного пласта достаточно сложен. Одновременно происходит удержание части твердой фазы суспензии в порах пласта и вынос части твердых частиц потоком дальше в пласт. Кроме того, часть ранее осевших частиц, попадая в фильтрационный поток, уносится им и оседает в более глубоких зонах пласта. Несмотря на малую величину, закольматированный слой создает значительные фильтрационные сопротивления особенно в случае применения водных промывочных жидкостей. Наибольший вклад в создание физико-математических основ кольматации и получение надежных экспериментальных данных внес Ю.М. Шехтман [1]. Многие положения его исследований актуальны до настоящего времени. Забивка порового пространства взвешенными в потоке жидкости твердыми частицами (кольматация) оказывает существенное влияние на многие реальные процессы. На этом явлении основаны методы очистки жидкостей от содержащихся в них примесей [1, 2]. Кольматация служит важным средством борьбы с фильтрационными потерями воды из каналов. Она является той причиной, которая порождает отложение частиц фильтрата бурового раствора на поверхности скважины и в прискважинной зоне, что приводит к снижению проводящих свойств пласта [3]. Annotation Blockage of the pores of the porous medium with solid particles (clogging) and the reverse process of detachment and transfer of particles deep into the porous medium (suffusion) occur both during the primary and secondary opening of the reservoirs. The process of mudding a productive formation is rather complicated. At the same time, a part of the solid phase of the suspension is retained in the pores of the formation and some of the solid particles are carried away by the flow further into the formation. In addition, some of the previously settled particles, getting into the filtration flow, are carried away by them and settle in deeper zones of the formation. Despite its small size, the clogged layer creates significant filtration resistance, especially in the case of using aqueous flushing fluids. Yu.M. Shekhtman [1]. Many provisions of his research are relevant to this day. The clogging of the pore space with solid particles suspended in the fluid flow (clogging) has a significant impact on many real processes. Methods for cleaning liquids from impurities contained in them are based on this phenomenon [1, 2]. Colmatation serves as an important means of combating filtration losses of water from canals. It is the reason that gives rise to the deposition of particles of drilling mud filtrate on the surface of the well and in the near-wellbore zone, which leads to a decrease in the conductive properties of the formation [3]. МОДЕЛИ КОЛЬМАТАЦИИ ПОРИСТЫХ СРЕД MODELS OF POROUS MEDIA COLMATION Ключевые слова. Пористая среда, твердые частицы, кольматация, обратный процесс, суффозия, пласты, фильтрация, фильтрационные сопротивления. Keywords. Porous medium, solid particles, clogging, reverse process, suffusion, formations, filtration, filtration resistance. Интегральные модели. Интегральные модели формулируются в терминах осредненных характеристик процесса: концентрации частиц взвеси с, пористости среды m и скорости фильтрации v. Приближенные уравнения для них рассматривались в работах [1-6]. Ограничимся одномерными течениями в направлении оси х. Скорости взвешенных частиц и самой взвеси считаем одинаковыми. Жидкость, частицы взвеси и скелет пористой среды в его начальном состоянии предполагаем несжимаемыми. При перемещении взвешенные частицы могут оставаться в потоке или задерживаться пористой средой, перекрывая входы в пору. Если последняя имеет несколько входов-выходов, она остается проточной. В противном случае пора вместе с частицей присоединяется к скелету пористой среды, причем образовавшаяся таким образом пористая матрица остается несжимаемой. Вклад таких (тупиковых) пор можно учитывать посредством параметра æ, смысл которого состоит в том, что захват каждой единицы объема частиц сопровождается образованием 1+æ объемов скелета пористой среды. При сформулированных условиях баланс объема твердой фазы, находящейся во взвеси или задержанной пористой средой, и баланс объема жидкости, содержащейся в потоке или отсеченной от него в процессе кольматации, могут быть представлены в виде 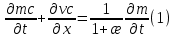 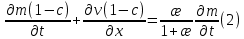 Для случая 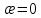 уравнение (1), записанное в иных терминах, получено в [7]. Следствием (1) и (2) является баланс объема взвеси уравнение (1), записанное в иных терминах, получено в [7]. Следствием (1) и (2) является баланс объема взвеси 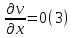 Уравнение кинетики кольматации, которое связывает скорость изменения пористости с параметрами потока, часто берется в виде [1, 8] 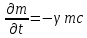 где 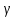 – некоторая положительная постоянная. Недостатком здесь является то, что задержка частиц происходит всегда, когда – некоторая положительная постоянная. Недостатком здесь является то, что задержка частиц происходит всегда, когда 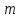 и и 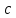 отличны от нуля. Кинетика более общего типа использовалась в [7] отличны от нуля. Кинетика более общего типа использовалась в [7]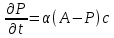 Здесь Р – доля объема пространства, приходящаяся на частицы, захваченные пористой средой, А - максимально возможное значение этой величины, 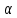 – эмпирическая постоянная. – эмпирическая постоянная.На самом деле параметр 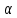 зависит от скорости фильтрации [9], поскольку интенсивность кольматации определяется не столько значением самой концентрации, сколько величиной всего потока частиц зависит от скорости фильтрации [9], поскольку интенсивность кольматации определяется не столько значением самой концентрации, сколько величиной всего потока частиц 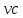 . Учитывая это, примем уравнение кинетики кольматации в виде . Учитывая это, примем уравнение кинетики кольматации в виде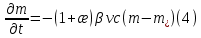 с некоторой эмпирической постоянной 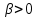 . .Течение взвеси обычно считают подчиняющимся закону Дарси [1] 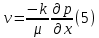 где 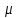 – вязкость взвеси, – вязкость взвеси, 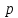 – давление в ней и – давление в ней и 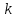 – проницаемость среды. Для последней используют эмпирические зависимости вида – проницаемость среды. Для последней используют эмпирические зависимости вида 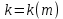 , среди которых наиболее распространена степенная [4-6]. , среди которых наиболее распространена степенная [4-6].Начальная и начально-краевая задача для линеаризованной системы (1)-(4) в случае 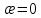 и для заданного постоянного расхода и для заданного постоянного расхода 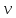 исследована в [7]. исследована в [7].Первая проблема, возникающая при использовании интегрального подхода связана с граничным условием на входе 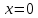 в пористый образец в пористый образец 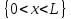 . Как правило, полагают, что концентрация взвешенных частиц . Как правило, полагают, что концентрация взвешенных частиц 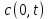 является заданной функцией времени является заданной функцией времени 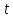 и равна концентрации и равна концентрации 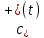 , с которой взвесь подводится к образцу [1, 3]. Такое предположение оправдано тогда, когда , с которой взвесь подводится к образцу [1, 3]. Такое предположение оправдано тогда, когда 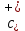 мало и частицы взвеси достаточно мелкие. Если этого нет, необходимо ставить условие мало и частицы взвеси достаточно мелкие. Если этого нет, необходимо ставить условие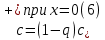 в котором параметр 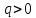 характеризует вероятность задержки частицы взвеси на входе в пористый образец. характеризует вероятность задержки частицы взвеси на входе в пористый образец.Вторая проблема связана с тем, что, как правило, на лицевой поверхности среды с течением времени нарастает слой отложенных частиц (фильтрационная корка), толщина которого 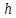 – заранее неизвестная функция времени. Для этого случая внутри корки – заранее неизвестная функция времени. Для этого случая внутри корки 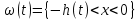 необходимо использовать уравнения (1)-(5) со значениями необходимо использовать уравнения (1)-(5) со значениями 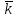 , , 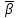 и и 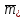 , отличными от значений параметров , отличными от значений параметров 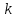 , , 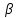 и и 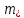 пористого образца. Пусть пористого образца. Пусть 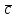 и и 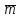 есть, соответственно, концентрация взвеси и пористость в есть, соответственно, концентрация взвеси и пористость в 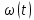 . Тогда в силу непрерывности скорости фильтрации при переходе через правый конец корки . Тогда в силу непрерывности скорости фильтрации при переходе через правый конец корки 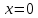 искомое условие на нем запишется в аналогичном (6) виде искомое условие на нем запишется в аналогичном (6) виде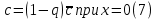 На подвижной границе 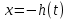 требуются два условия. Первое из них представляет собой баланс объема частиц, задерживаемых на входе в корку, и описывается равенством требуются два условия. Первое из них представляет собой баланс объема частиц, задерживаемых на входе в корку, и описывается равенством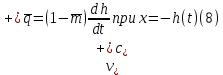 где 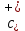 и и 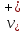 – соответственно концентрация и скорость подачи взвеси извне корки, а – соответственно концентрация и скорость подачи взвеси извне корки, а 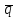 – вероятность задержки частицы на ее входной поверхности. – вероятность задержки частицы на ее входной поверхности.Второе условие выражает баланс объема взвеси как целого и означает, что 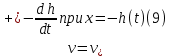 Определяющие соотношения. Интегральные подходы порождают соответствующую проблему определяющих соотношений. Суть ее в том, что входящие в указанные модели величины 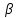 , , 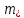 и и 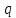 меняются искомым образом как по координате, так и со временем. В общем случае зависит от характеристик потока заранее неизвестным образом и проницаемость меняются искомым образом как по координате, так и со временем. В общем случае зависит от характеристик потока заранее неизвестным образом и проницаемость 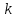 . Оставаясь в рамках интегральных моделей, объяснить подобные изменения не представляется возможным, необходим переход к более детальному описанию поровой структуры и состава взвеси. С этой целью используем подход, предложенный в работе [10]. . Оставаясь в рамках интегральных моделей, объяснить подобные изменения не представляется возможным, необходим переход к более детальному описанию поровой структуры и состава взвеси. С этой целью используем подход, предложенный в работе [10].Ограничимся далее случаем 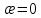 и рассмотрим течение монодисперсной взвеси с радиусом взвешенных частиц и рассмотрим течение монодисперсной взвеси с радиусом взвешенных частиц 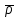 . Каждый элементарный объем пористой среды представим состоящим из перпендикулярных потоку слоев-сит толщины . Каждый элементарный объем пористой среды представим состоящим из перпендикулярных потоку слоев-сит толщины 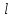 , зависящей искомым образом от координаты элементарного объема и времени. Поровое пространство слоя схематизируем набором цилиндров с направленной по потоку осью длины , зависящей искомым образом от координаты элементарного объема и времени. Поровое пространство слоя схематизируем набором цилиндров с направленной по потоку осью длины 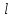 и случайно распределенным радиусом и случайно распределенным радиусом 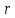 . Обозначим через . Обозначим через 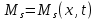 число этих пор-каналов на единице площади слоя, и пусть число этих пор-каналов на единице площади слоя, и пусть 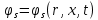 – плотность распределения их по радиусам. Если – плотность распределения их по радиусам. Если 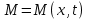 – число пор в единице объема пространства, то – число пор в единице объема пространства, то 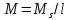 . Считаем слои вероятностно независимыми в том смысле, что если частица взвеси прошла через одну из пор слоя, она попадет на вход канала радиуса . Считаем слои вероятностно независимыми в том смысле, что если частица взвеси прошла через одну из пор слоя, она попадет на вход канала радиуса 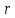 следующего слоя с вероятностью, определяемой лишь функцией следующего слоя с вероятностью, определяемой лишь функцией 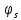 . .В рамках подобной схематизации порового пространства уравнение кинетики кольматации (4) может быть записано в виде 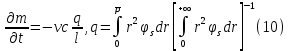 Входящая в правую часть этого уравнения величина 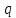 зависит от зависит от 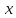 и и 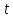 через функцию распределения через функцию распределения 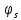 и представляет собой вероятность задержки частицы взвеси отдельно взятым слоем. Указанная величина присутствует и в краевых условиях (6)-(8). и представляет собой вероятность задержки частицы взвеси отдельно взятым слоем. Указанная величина присутствует и в краевых условиях (6)-(8).Функция распределения каналов на слое по радиусам 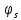 и числовая плотность пор в объеме и числовая плотность пор в объеме 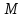 определяются из уравнений определяются из уравнений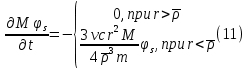 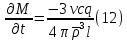 Толщина слоев 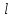 меняется таким образом, что сохраняется соотношение меняется таким образом, что сохраняется соотношение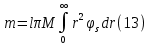 связывающее характеристики слоев 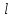 и и 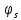 объемными величинами объемными величинами 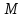 и и 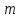 . Равенство (13) означает совпадение поверхностной и объемной пористостей. . Равенство (13) означает совпадение поверхностной и объемной пористостей.Можно подсчитать изменения пропускной способности слоев рассматриваемого элементарного объема, когда на лицевых гранях последнего фиксирован перепад давления. Последующее сравнение с законом Дарси (5) показывает тогда, что снижение проницаемости среды описывается уравнением 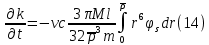 Для целей настоящего исследования особый интерес представляют равновесные режимы течения, в которых влиянием временных и пространственных границ можно пренебречь и учитывать лишь внутренние особенности самого процесса. Таким режимам соответствуют решения систем (1), (10)-(13), в которых скорость фильтрации 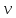 – заданная постоянная, а функции – заданная постоянная, а функции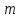 , , 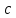 , , 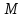 , , 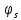 и и 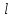 зависят от зависят от 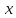 и и 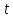 только через переменную только через переменную 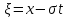 , где , где 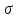 – искомая скорость простой волны. Эти решения связывают невозмущенное состояние перед волной – искомая скорость простой волны. Эти решения связывают невозмущенное состояние перед волной 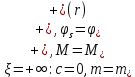 с возникшим после ее прохождения некоторым стабилизированным состоянием 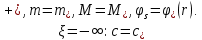 Здесь 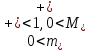 и и 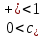 – заданные параметры, – заданные параметры, 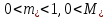 – искомые, – искомые, 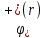 – заданная функция, – заданная функция, 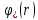 – искомая. – искомая.Скорость перемещения равновесного режима определяется соотношением 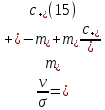 Это означает, что поступающий с потоком объем частиц 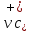 разбивается на две составляющие: первая, равная разбивается на две составляющие: первая, равная 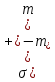 , задерживается пористой средой, а вторая, равная , задерживается пористой средой, а вторая, равная 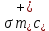 , переносится вместе с потоком. В этих условиях реализуется простая зависимость концентрации от пористости и скорости распространения волны: , переносится вместе с потоком. В этих условиях реализуется простая зависимость концентрации от пористости и скорости распространения волны: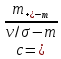 Представление для числовой плотности пор здесь приобретает вид 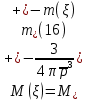 В равновесном режиме функция плотности распределения пор на слое по радиусам оказывается связанной с концентрацией частиц во взвеси и пористостью среды соотношением 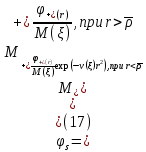 где 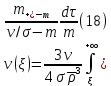 Это позволяет получить для пористости для пористости представление 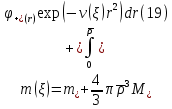 Входящие в указанные зависимости искомые параметры 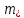 , , 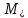 и и 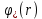 находятся из следующих соображений. Пористость находятся из следующих соображений. Пористость 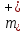 , числовая плотность каналов , числовая плотность каналов 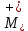 и функция и функция 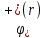 задают состояние поровой структуры перед волной. Условие нормировки для плотности вероятности задают состояние поровой структуры перед волной. Условие нормировки для плотности вероятности 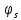 оказывается эквивалентным требованию, чтобы оказывается эквивалентным требованию, чтобы 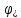 и и 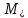 определялись выражениями определялись выражениями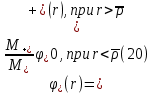 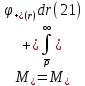 Искомое представление для параметра 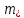 получается переходом в (16) к пределу получается переходом в (16) к пределу 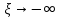 : :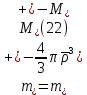 Соотношения (18), (19) вместе с (15), (20)-(22) образуют систему двух нелинейных уравнений, из которых должны находиться зависимости 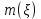 и и 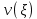 . Принципиальным моментом здесь является возможность исключения продольной координаты . Принципиальным моментом здесь является возможность исключения продольной координаты 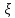 . С этой целью вводятся параметр . С этой целью вводятся параметр 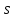 , меняющийся в диапазоне , меняющийся в диапазоне 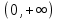 , и вспомогательная функция , и вспомогательная функция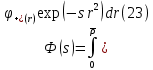 В терминах этой функции выражение (19) для пористости приводится к виду 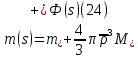 Отсюда из соотношения (13) и из (17) находится взаимосвязь между шириной слоев 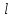 и значениями параметра и значениями параметра 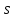 : :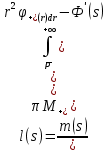 В случае равновесного режима уравнение (14) сводится к обыкновенному дифференциальному уравнению 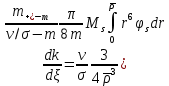 После подстановки в него функции 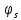 ее выражения из (17), найдем, что ее выражения из (17), найдем, что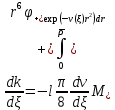 где 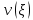 определена согласно (18). Решение этого уравнения легко находится, поскольку в силу (23), (24) и (19) определена согласно (18). Решение этого уравнения легко находится, поскольку в силу (23), (24) и (19) 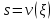 , и в результате получается сравнительно простое выражение проницаемости в виде функции параметра , и в результате получается сравнительно простое выражение проницаемости в виде функции параметра 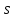 : :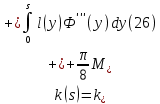 Входящая сюда величина 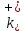 есть значение проницаемости невозмущенного состояния перед волной. есть значение проницаемости невозмущенного состояния перед волной.Вероятность 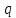 задержки слоем частицы, как следует из (10), соотношения (13), выражения (17) для функции распределения задержки слоем частицы, как следует из (10), соотношения (13), выражения (17) для функции распределения 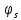 и зависимости и зависимости 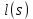 из (25), может быть представлена в виде из (25), может быть представлена в виде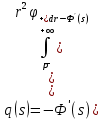 Сравнивая (10) и (4) (при 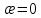 ) и учитывая (17), получаем, что ) и учитывая (17), получаем, что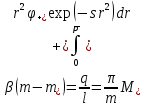 Отсюда и из (24) находится искомое представление для параметра 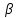 : :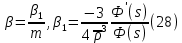 Схема построения определяющих соотношений для интегральных моделей выглядит теперь следующим образом. Начальное состояние среды в текущей точке определяет величины 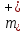 , , 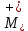 и и 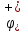 . С их использованием из (20)-(22) находится параметр . С их использованием из (20)-(22) находится параметр 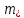 . Затем для значений пористости . Затем для значений пористости 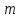 из отрезка из отрезка 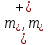 с помощью (23) и (24) определяется зависимость с помощью (23) и (24) определяется зависимость 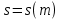 . Она подставляется в равенства (25)-(28) и в результате возникают требуемые определяющие соотношения . Она подставляется в равенства (25)-(28) и в результате возникают требуемые определяющие соотношения 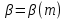 , , 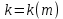 и и 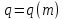 . .В заключение отметим, что, во-первых, как показывает проведенный анализ, более содержательной физически является запись уравнения (4) в виде 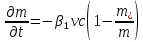 где 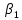 определяется согласно (28). Преимущество такой формы уравнения кинетики кольматации в том, что стоящий в круглых скобках сомножитель в правой части уравнения хотя бы качественно можно интерпретировать как вероятность задержания частицы взвеси в элементарном объеме пористой среды. Количественные оценки требуют расчетов зависимости определяется согласно (28). Преимущество такой формы уравнения кинетики кольматации в том, что стоящий в круглых скобках сомножитель в правой части уравнения хотя бы качественно можно интерпретировать как вероятность задержания частицы взвеси в элементарном объеме пористой среды. Количественные оценки требуют расчетов зависимости 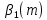 . .Во-вторых, согласно (27) 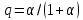 , где , где 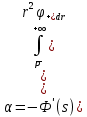 Поэтому в классическом варианте ( 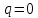 ) граничное условие (6) реализуется лишь тогда, когда либо пористая среда в своем начальном состоянии почти не содержит поровых каналов с радиусом, меньшим радиуса взвешенных частиц, либо по происшествии достаточно длительного времени, когда на входной поверхности среды практически выполняется равенство ) граничное условие (6) реализуется лишь тогда, когда либо пористая среда в своем начальном состоянии почти не содержит поровых каналов с радиусом, меньшим радиуса взвешенных частиц, либо по происшествии достаточно длительного времени, когда на входной поверхности среды практически выполняется равенство 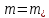 . .В области 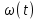 , занятой фильтрационной коркой, для описания ее неоднородности по глубине принято вводить дополнительные приближенные зависимости [3]. При использовании представленного в настоящей работе подхода достаточно знать лишь значения параметров , занятой фильтрационной коркой, для описания ее неоднородности по глубине принято вводить дополнительные приближенные зависимости [3]. При использовании представленного в настоящей работе подхода достаточно знать лишь значения параметров 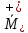 , , 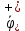 и и 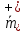 на ее лицевой поверхности на ее лицевой поверхности 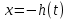 . Эти значения не меняются со временем, и неоднородность корки по глубине формируется в соответствии с уравнениями (1)-(5), граничными условиями (8), (9) и полученными выше определяющими соотношениями. . Эти значения не меняются со временем, и неоднородность корки по глубине формируется в соответствии с уравнениями (1)-(5), граничными условиями (8), (9) и полученными выше определяющими соотношениями.ЛИТЕРАТУРА 1. Шехтман Ю.М. Фильтрация малоконцентрированных суспензий, М., «Недра», 1961, с.125-130. Dickey G.D. Filtration. N.Y.: Reinhold Publishing Corp., 1961. Михайлов Н.Н. Изменение физических свойств горных пород в около- скважинных зонах. М.: Недра, 1987. Зубарев А.Ю., Хужаеров Б. К теории релаксационной фильтрации // Инж.-физ. журн. 1988. Т.55, №3. С.442-447. Хужаеров Б. Влияние кольматации и суффозии на фильтрацию суспензий //Инж.-физ. журн. 1990. Т.58, №2. С.244-250. Хужаеров Б. Модель фильтрации суспензии с учетом кольматации и суффозии //Инж.-физ. журн. 1992. Т.63, №1. С.72-79. Litwiniszyn J. On suspension flow in a porous medium //Int. J. Eng. Sci. 1967. V.5, №5. P.435-454. Sahimi M., Imdaki A.O. Hydrodynamics of particulate motion in porous media //Phys. Rev. Lett. 1991. V.60, №9. P.1169-1172. Trzaska A. Experemental research on the phenomenon of colmatage //Bull. Acad. Pol. Sci. Ser. Sci. Techn. 1965. V.13, №9. P.451-457. Капранов Ю.И. Структурная модель процесса механической кольматации пористой среды //Динамика сплошной среды: Сб.научн.тр. /АН СССР. Сиб.отд-ние. Ин-т гидродинамики. 1989. Вып.90. С.27-39. Касперский Б.В. Проникновение твердой фазы глинистых растворов в пористую среду, «Нефтяное хозяйство», 1971, №9, с. 30-32. Касперский Б.В. Исследование проникновения твердой фазы промывочных жидкостей в условиях высоких температур в гранулярную пористую среду. Материалы диссертации на соискание доктора технических наук, 1975, с.39-87. Степанов Н.В. Моделирование и прогноз осложнений при бурении скважин, М., Изд. «Недра», с.65-82. |
