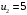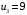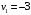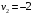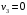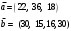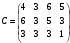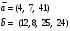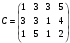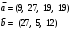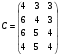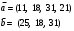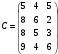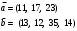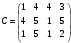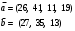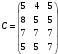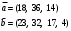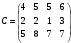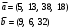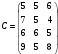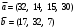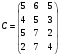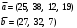для выдачи. Транспортная задача необходимые сведения
 Скачать 371.46 Kb. Скачать 371.46 Kb.
|
ТРАНСПОРТНАЯ ЗАДАЧАНеобходимые сведенияВажным частным случаем задачи линейного программирования является транспортная задача. Необходимо определить план перевозок некоторого однородного груза, минимизирующий затраты на общую стоимость перевозок, из 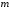 пунктов отправления (производства) пунктов отправления (производства) 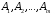 в в  пунктов потребления пунктов потребления 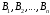 . .Введем следующие переменные: 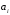 – величина предложения продукта в пункте – величина предложения продукта в пункте 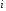 , , 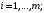 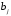 – величина спроса на продукт в пункте – величина спроса на продукт в пункте 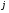 , , 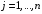 ; ;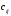 – затраты на транспортировку единицы продукта из пункта – затраты на транспортировку единицы продукта из пункта 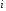 в пункт в пункт 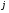 ; ;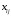 – количество продукта, перевозимого из пункта – количество продукта, перевозимого из пункта 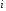 в пункт в пункт 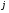 . .Тогда транспортную задачу можно представить в виде таблицы 1. Т а б л и ц а 2.1
В сделанных обозначениях математическую модель транспортной задачи можно записать следующим образом: 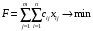 (2.1) (2.1)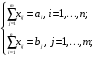 (2.2) (2.2)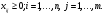 (2.3) (2.3)Существует несколько вариантов транспортной задачи. Закрытая транспортная задача Общий спрос равен общему предложению: 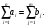 Это равенство является необходимым и достаточным условием существования допустимого плана задачи (2.1) – (2.3). Открытая транспортная задача а) Пусть существует излишек продукта, т.е. 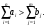 б) Пусть существует дефицит продукта, т.е. 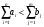  Такую задачу можно свести к закрытой задаче, вводя дополнительный столбец (строку), равный по величине имеющейся разности между общим спросом и общей потребностью, тарифы 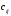 которого считают условно равными нулю. которого считают условно равными нулю.Транспортная задача с фиксированными перевозками Если объем перевозок между пунктами 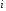 и и 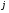 задан, то в задаче (2.1) – (2.3) вводится дополнительное ограничение задан, то в задаче (2.1) – (2.3) вводится дополнительное ограничение 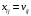 , где , где 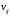 – заданный объем перевозок. – заданный объем перевозок.Если объем перевозок из пункта 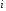 в в 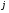 пункт ограничен величиной пункт ограничен величиной 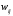 , то в задаче (2.1) – (2.3) вводится дополнительное ограничение , то в задаче (2.1) – (2.3) вводится дополнительное ограничение 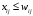 . .Все приведенные выше модели описывают транспортную задачу в виде задачи линейного программирования. В этой форме она может быть решена стандартными средствами ЛП, например, с помощью симплекс-метода. Однако специфичная форма системы ограничений данной задачи (в виде уравнений-равенств) позволяет существенно упростить обычный симплекс-метод. Такой метод решения транспортной задачи (ТЗ) называют распределительным, или методом потенциалов. По аналогии с общим случаем ЗЛП, решение в нем осуществляется по трем шагам: нахождение первоначального опорного решения; проверка критерия оптимальности; переход к следующему опорному решению. Методы нахождения первоначального распределения поставок Все существующие методы нахождения опорных планов отличаются только способом выбора клетки для заполнения. Само заполнение происходит одинаково независимо от используемого метода. Следует помнить, что перед нахождением опорного плана транспортная задача должна быть сбалансирована (приведена к закрытой модели). Метод северо-западного угла На каждом шаге этого метода из всех не вычеркнутых клеток выбирается самая левая и верхняя (северо-западная) клетка. Другими словами, на каждом шаге выбирается первая из оставшихся не вычеркнутых строк и первый из оставшихся не вычеркнутых столбцов. Для того чтобы заполнить клетку 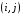 , необходимо сравнить текущий запас товара в рассматриваемой i-й строке , необходимо сравнить текущий запас товара в рассматриваемой i-й строке 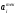 с текущей потребностью в рассматриваемом j-м столбце с текущей потребностью в рассматриваемом j-м столбце 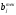 . .Если существующий запас позволяет перевезти всю потребность, то в клетку 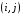 в качестве перевозки вписывается значение потребности в качестве перевозки вписывается значение потребности 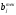 ; ;j-й столбец вычеркивается, поскольку его потребность уже исчерпана; от существующего запаса в i-й строке отнимается величина сделанной перевозки, прежний запас зачеркивается, а вместо него записывается остаток, т.е. 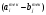 . .Если существующий запас не позволяет перевезти всю потребность, то в клетку 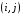 в качестве перевозки вписывается значение запаса в качестве перевозки вписывается значение запаса 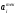 ; ;i-я строка вычеркивается, поскольку ее запас уже исчерпан; от существующей потребности в j-й строке отнимается величина сделанной перевозки, прежняя потребность зачеркивается, а вместо нее записывается остаток, т.е. 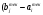 ). ).Нахождение опорного плана продолжается до тех пор, пока не будут вычеркнуты все строки и столбцы. Если на некотором шаге вычеркиваются одновременно строка и столбец, то либо по строке, либо по столбцу рядом необходимо записать «0»-поставку и при дальнейших расчетах считать эту клетку условно заполненной. Метод минимальных затрат (минимального элемента) На каждом шаге этого метода из всех не вычеркнутых клеток транспортной матрицы выбирается клетка с минимальной стоимостью перевозки 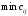 .. Заполнение выбранной клетки производится по правилам, описанным выше. .. Заполнение выбранной клетки производится по правилам, описанным выше.Метод потенциалов решения транспортной задачи Распределение поставок называется базисным, если переменные, соответствующие заполненным клеткам, можно принять за основные (базисные) переменные. Клетки, соответствующие свободным переменным, остаются незаполненными (пустыми). Теорема: число  базисных переменных закрытой транспортной задачи равно базисных переменных закрытой транспортной задачи равно 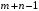 , где , где 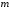 – число поставщиков, – число поставщиков, – число потребителей. – число потребителей.Критерий оптимальности опорного решения ТЗ: распределение поставок оптимально тогда и только тогда, когда оценки всех свободных клеток неотрицательны. Теорема о потенциалах: Оценка свободной клетки не изменится, если к коэффициентам затрат некоторой строки (столбца) таблицы поставок прибавить некоторое число. Это число, прибавляемое к коэффициентам затрат выделенной строки (столбца), будем называть потенциалом данной строки (столбца). Следствие (правило нахождения оценок свободных клеток): к коэффициентам затрат таблицы поставок в каждой строке и столбце надо прибавить такие числа (потенциалы), чтобы коэффициенты затрат в заполненных клетках стали равными нулю. Полученные при этом коэффициенты затрат свободных клеток равны оценкам этих клеток. При переходе к следующему опорному решению, т.е. в результате ввода нового элемента в базис, нарушается общий баланс ресурсов и потребностей. Для того чтобы привести его в норму, необходимо преобразовать некоторые базисные элементы по какому-нибудь замкнутому циклу для сохранения баланса по строкам и столбцам таблицы поставок. Циклом пересчета называется такой цикл в таблице с базисным распределением поставок, при котором одна из его вершин лежит в свободной клетке, а остальные – в заполненных. Цикл пересчета называется означенным, если в его вершинах расставлены знаки «+» и «-» так, что в свободной клетке стоит знак «+», а соседние вершины имеют противоположные знаки. Объем поставки, передаваемой по циклу, определяют, как наименьшее из чисел, стоящих в вершинах цикла со знаком «-». Циклы встречаются самые разные. Например, следующих видов:
Рис.2.1. Виды циклов пересчета в распределении поставок транспортной задачи Методические указания к решению типовых задачНа трех складах оптовой базы сосредоточен однородный груз в количествах 200, 300 и 500 ед. Этот груз необходимо перевезти в четыре магазина. Каждый из магазинов должен получить соответственно 200, 200, 300 и 400 ед. груза. Тарифы перевозок единицы груза из каждого из складов во все магазины задаются матрицей: 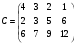 Требуется: 1) составить экономико-математическую модель задачи; 2) найти первоначальное распределение поставок: а) методом северо-западного угла; б) методом минимальных затрат. 3) выбрать лучшее распределение поставок и найти такой план перевозок, при котором общая стоимость перевозок будет минимальной. Решить транспортную задачу методом потенциалов. Решение: 1) составление экономико-математической модели ТЗ Искомый объем перевозки от i-ro поставщика к j-му потребителю обозначим 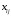 и назовем поставкой клетки и назовем поставкой клетки 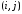 . Заданные объемы груза, имеющегося на базах, и спросы магазинов накладывают ограничения на значения неизвестных. Получаем следующую систему ограничений из уравнений баланса по строкам и столбцам. . Заданные объемы груза, имеющегося на базах, и спросы магазинов накладывают ограничения на значения неизвестных. Получаем следующую систему ограничений из уравнений баланса по строкам и столбцам.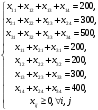 Транспортная задача – задача на минимум. Поэтому целевая функция имеет вид: 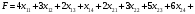 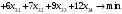 2) найдем первоначальное распределение поставок (опорное решение) Проверим выполнение необходимого и достаточного условия разрешимости задачи – условие закрытости модели. 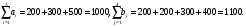 Имеем открытую модель транспортной задачи, необходимо сбалансировать общие итоги. Вводим 4-го, фиктивного поставщика с запасами 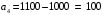 и нулевыми стоимостями перевозок единиц груза. а) Построим первоначальное распределение поставок методом северо-западного угла: Распределим запасы первой базы. Так как ее запасы 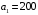 равны потребностям первого магазина равны потребностям первого магазина 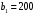 , необходимо ввести условную нулевую поставку, например, по строке. Из дальнейшего рассмотрения исключаются первая строка и первый столбец (см. табл.2.2) , необходимо ввести условную нулевую поставку, например, по строке. Из дальнейшего рассмотрения исключаются первая строка и первый столбец (см. табл.2.2)Т а б л и ц а 2.2
Распределим запасы второй базы. Так как ее запасы 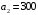 больше потребностей второго магазина больше потребностей второго магазина 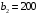 , в клетку , в клетку 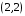 вносим число 200, вычеркиваем второй столбец и запоминаем, что остатки груза на второй базе составляют вносим число 200, вычеркиваем второй столбец и запоминаем, что остатки груза на второй базе составляют 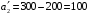 (см. табл.2.3) (см. табл.2.3)Т а б л и ц а 2.3
Распределим остатки запасов второй базы. Так как ее запасы 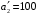 меньше потребностей третьего магазина меньше потребностей третьего магазина 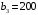 , в клетку , в клетку 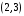 вносим число 100, вычеркиваем вторую строку и запоминаем, что третьему магазину следует допоставить 100 ед. груза ( вносим число 100, вычеркиваем вторую строку и запоминаем, что третьему магазину следует допоставить 100 ед. груза (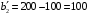 ) (см. табл.2.4) ) (см. табл.2.4)Т а б л и ц а 2.4
Последовательно выполняя такие действия, получаем первоначальное распределение поставок по методу северо-западного угла, приведенное в таблице 2.5. Т а б л и ц а 2.5
Полученное решение 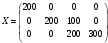 является базисным, т.к. выполняется необходимое и достаточное условие является базисным, т.к. выполняется необходимое и достаточное условие 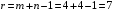 . Найдем значение целевой функции для полученного решения . Найдем значение целевой функции для полученного решения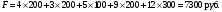 б) Построим первоначальное распределение поставок методом наименьших затрат (минимальной стоимости): Среди элементов стоимостей выбираем наименьшую стоимость (без учета нулевых стоимостей условной, четвертой базы) 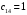 . В соответствующую клетку записываем максимально возможную поставку . В соответствующую клетку записываем максимально возможную поставку 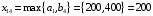 . Потребности 4-го магазина уменьшаем на 400-200=200, вычеркиваем первую строку (табл.2.6). . Потребности 4-го магазина уменьшаем на 400-200=200, вычеркиваем первую строку (табл.2.6).Т а б л и ц а 2.6
В оставшейся части таблицы поставок также определяем элемент с наименьшим тарифом – это 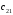 =2. Здесь наибольшая возможная поставка составит =2. Здесь наибольшая возможная поставка составит 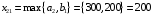 , запасы второй базы уменьшаем до 100 ед., вычеркиваем первый столбец – табл.2.7. , запасы второй базы уменьшаем до 100 ед., вычеркиваем первый столбец – табл.2.7.Т а б л и ц а 2.7
Продолжая таким же образом, получаем первоначальное распределение поставок методом минимальной стоимости, приведенное в таблице 2.8. Т а б л и ц а 2.8
Полученное решение имеет 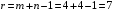 базисных переменных. Вычислим значение целевой функции на этом опорном решении базисных переменных. Вычислим значение целевой функции на этом опорном решении 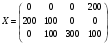 . . 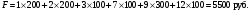 Сравнивая значения целевых функций для опорных планов, полученных методами северо-западного угла и минимальной стоимости, делаем вывод, что целевая функция для второго случая ближе к минимуму. 3) проверка критерия оптимальности найденного решения По признаку оптимальности в каждой занятой опорным решением таблицы ТЗ сумма потенциалов равна стоимости ( 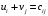 при при 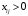 ). Составим систему уравнений для нахождения потенциалов строк и столбцов матрицы поставок ). Составим систему уравнений для нахождения потенциалов строк и столбцов матрицы поставок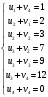 Система состоит из семи уравнений и имеет восемь переменных. Система неопределенная. Одной переменной задаем произвольное значение (пусть 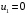 ). Остальные значения потенциалов находятся однозначно: ). Остальные значения потенциалов находятся однозначно:
Вычислим оценки свободных клеток с учетом найденных потенциалов: 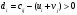 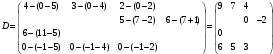 Критерий оптимальности не выполняется, т.к. 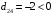 . . - переход к следующему опорному решению Для перехода к следующему базисному решению построим цикл для клетки (2,4) – загрузим ее поставкой (см. табл. 2.9). Т а б л и ц а 2.9
Определим поставку, передаваемую по циклу 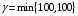 (как наименьшее из чисел, находящихся в вершинах цикла со знаком «-»). Клетку (3,4) с тарифом (как наименьшее из чисел, находящихся в вершинах цикла со знаком «-»). Клетку (3,4) с тарифом 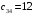 будем считать свободной. Следующее базисное распределение представлено в таблице 2.10 будем считать свободной. Следующее базисное распределение представлено в таблице 2.10Т а б л и ц а 2.10
Проверим найденное решение на оптимальность. Составим систему уравнений для нахождения потенциалов строк и столбцов новой матрицы поставок 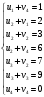 Пусть 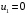 , тогда , тогда
Вычислим оценки свободных клеток с учетом найденных потенциалов и проверим выполнение критерия оптимальности: 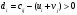 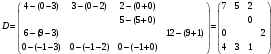 Критерий оптимальности выполняется, следовательно, найденное опорное решение оптимально. Найдем минимальное значение стоимости перевозок: 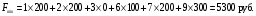 Ответ: 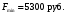 при при 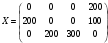 . . Задание для самостоятельной работыНа складах оптовой базы сосредоточен однородный груз в некоторых количествах 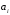 ед. Этот груз необходимо перевезти в магазины. Каждый из магазинов должен получить груз объемом ед. Этот груз необходимо перевезти в магазины. Каждый из магазинов должен получить груз объемом 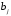 соответственно. Тарифы перевозок единицы груза из каждого из складов во все магазины заданы матрицей соответственно. Тарифы перевозок единицы груза из каждого из складов во все магазины заданы матрицей 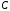 . Требуется: . Требуется: 1) составить экономико-математическую модель задачи; 2) найти первоначальное распределение поставок: а) методом северо-западного угла; б) методом минимальных затрат. 3) выбрать лучшее распределение поставок и найти такой план перевозок, при котором общая стоимость перевозок будет минимальной. Решить транспортную задачу методом потенциалов. Варианты данных:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

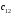
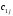
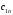
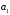
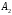
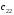
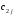
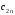
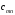
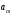
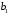
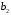


 00
00
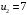
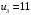
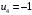
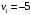
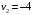
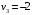
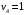
 00
00