финансовые вычисление ТГУ. финансовые вычесления. Условие задания

• Название: Условие задания
• Анкор: финансовые вычисление ТГУ
• Дата: 29.03.2023
• Размер: 86.34 Kb.
• Имя файла: финансовые вычесления.docx
• Тип: Решение; #1022750

Бланк выполнения задания 1

Условие задания.

Кредит размером 1,2 млн руб. выдан 15 февраля до 7 ноября включительно под 17 % годовых. Какую сумму должен вернуть должник в конце срока, если начисляются простые проценты. При решении задачи используйте три способа расчета простых процентов:

Первый способ. Начисление точных процентов с точным числом дней ссуды.

Второй способ. Начисление обыкновенных процентов с точным числом дней ссуды.

Третий способ. Начисление обыкновенных процентов с приближенным числом дней ссуды.

Решение задания:

1. 
   Определите сумму долга первым способом ( 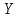= 365).
   
2. 
   Определите сумму долга вторым способом ( 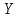= 360).
   
3. 
   Определите сумму долга третьим способом ( 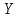= 360).
   

При решении необходимо использовать следующую формулу.

,

где – наращенная сумма ссуды;

– первоначальная сумма долга;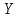

– временная база;

– число дней ссуды;

– годовая процентная ставка.

4. 
   Определите, какой из способов для должника предпочтительнее.
   Решение:
   Осуществляем срок пользования кредитом:
   1) если в расчет принимается точное число дней ссуды:
   14 дней февраля (с 15 по 28-е число),
   31 день марта,
   

30 дней апреля,
31 день мая,
30 дней июня,
31 день июля,
31 день августа,
30 дней сентября,
31 день октября,
7 дней ноября (с 1 по 7-е число).
И из полученной суммы вычитаем единицу, поскольку дата выдачи и дата погашения кредита всегда считаются за один день.
Суммируем и получаем:
dточн=14+31+30+31+30+31+31+30+31+7-1=265
2) если в расчет принимается приближенное число дней ссуды:
14 дней февраля (с 15 по 28-е число), 8 месяцев (с марта по октябрь включительно) по 30 дней, 7 дней ноября (с 1 по 7-е число).
Таким образом:

dприбл=14+8x30+7-1=260
Первый способ – это английская практика начисления процентов. В данном случае осуществляется начисление точных процентов с точным числом дней ссуды. Это означает, что период начисления процентов равен фактическому сроку(dточн =265дней), продолжительность года Т=365 дней. Наращенная сумма кредита равна:

S=1200000x(1+265/365x0.17)=1348110
Второй способ – это французская практика, когда начисление обыкновенных процентов осуществляется с учетом точного числа дней ссуды. Это означает, что период начисления процентов равен фактическому сроку (dточн=265), продолжительность года Т=360 дней. Наращенная сумма кредита равна:
S=1200000x(1+265/360x0.17)=1350167
Третий способ – это немецкая практика, когда начисление обыкновенных процентов с учетом приближенного числа дней ссуды. Это означает, что один полный месяц равен 30 дням (dприбл=260дней ), продолжительность года Т=360 дней. Наращенная сумма кредита равна:
S=1200000x(1+260/360x0.17)=1347333
Таким образом, если используется английская практика начисления процентов, заемщик должен вернуть банку 1 348 110 руб.; если французская практика – 1 350 167 руб.; если немецкая практика – 1.347.333 руб.

Бланк выполнения задания 2

Условие задания.

Клиент открыл счет в банке и поместил на него сумму в размере 25 000 руб. Сложная годовая процентная ставка 11 %. Через два года и 164 дня клиент закрыл счет. Определите двумя методами, какую сумму получил клиент в случае начисления точных процентов. Какой метод расчета предпочтительнее для клиента, а какой выгоднее для банка?

Решение задания:

1. Определите сумму долга первым методом, используя формулу:

,

где – наращенная сумма ссуды;

– первоначальная сумма долга;

– годовая процентная ставка;

– число лет наращения.
2. Определите сумму долга вторым методом, используя формулу:

,

где 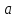– целое число лет;

– дробная часть года.
3. Сделайте вывод.

Решение:

Наращенная сумма при расчете первым способом составит:

32 281,24 руб.

Расчет наращенной суммы при смешанном способе начисления процентов (второй способ):

32 324,90 руб.

Наращенная сумма при использовании 1-го метода составит 32281,24 руб.; при использовании 2-го метода – 32324,90 руб. Для клиента предпочтительнее 2-й метод, т.к. наращенная сумма больше.

Бланк выполнения задания 3

Условие задания.

Ежегодно в течение 6 лет на банковский счет в конце года поступает 12 000 руб. На эти средства ежеквартально начисляются проценты по номинальной ставке 15 % годовых. Рассчитайте, какая сумма будет накоплена на банковском счете к концу указанного срока. Определите, как изменится итоговая сумма, если начисление процентов будет происходить ежемесячно.

Решение задания:

Поскольку денежные средства поступают на банковский счет в конце каждого года, то в результате образуется рента постнумерандо. Следовательно, для решения задачи необходимо приметь следующую формулу:

,

где 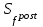– наращенная сумма годовой финансовой ренты постнумерандо;

– размер годового платежа;

– срок ренты;

– годовая процентная ставка;

– количество начислений процентов в год.
1. Определите сумму, аккумулированную на банковском счете в конце срока, если проценты начисляют ежеквартально.

2. Определите сумму, аккумулированную на банковском счете в конце срока, если проценты начисляют ежемесячно.

3. Сделайте вывод о том, какой вариант начисления процентов предпочтительнее для банка.

Решение:

Расчет наращенной суммы ренты:



Если начисление процентов будет происходить ежемесячно, то:



При ежеквартальном начислении процентов наращенная сумма ренты составит 107363,46 руб.; при ежемесячном начислении – 107935,03 руб. При начислении процентов ежемесячно итоговая сумма будет на 571,56 руб. больше. Для клиента выгоднее ежемесячное начисление процентов.

Бланк выполнения задания 4

Условие задания.

Для облигации номиналом 10 500 руб., выпущенной на 3 года, определен следующий порядок выплат: первый год – 10 %; далее каждый год процентная ставка повышается на 1,5 %. Определите наращенную стоимость облигации. Как изменится эта сумма, если процентная ставка в первый год начисления составит 12 %.

Решение задания:

1. Определите наращенную стоимость облигации по формуле:

,

где – наращенная сумма ссуды;

– первоначальная сумма долга;

– годовая процентная ставка;

– число лет наращения.
2. Определите наращенную стоимость облигации по вышеприведенной формуле при условии изменения ставки наращения в первый год начисления процентов.

Решение:

Расчет наращенной стоимости облигации:



Расчет наращенной стоимости облигации, если процентная ставка в первый год начисления составит 12 %: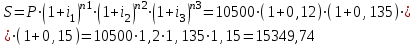



Наращенная стоимость облигации при ставках наращения 10%, 11,5% и 13% составит 14552,42 руб. А при ставках 12%, 13,5% и 15% наращенная сумма составит 15349,74 руб.

Бланк выполнения задания 5

Условие задания.

Четыре платежа в размере 25 000 руб. в конце первого года, 20 000 руб. в конце второго года, 35 000 руб. в конце третьего года, 40 000 руб. в конце четвертого года образуют ренту постнумерандо. Размер годовой процентной ставке 18 %. Определите наращенную сумму финансовой ренты постнумерандо к концу четвертого года. На сколько изменится эта сумма, если размер годовой процентной ставки увеличится на 3%.
Решение задания:
1. Определите современную стоимость переменной ренты постнумерандо путем приведения каждого ее платежа с помощью дисконтирования к началу первого периода и последующего суммирования (при = 18 %):
,
где 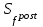– наращенная сумма годовой финансовой ренты постнумерандо;

– размер годового платежа;

– годовая процентная ставка.

2. Определите современную стоимость переменной ренты постнумерандо путем приведения каждого ее платежа с помощью дисконтирования к началу первого периода и последующего суммирования (при = 21 %).

3. Сравните полученные результаты и сделайте выводы.
Решение:

Находим наращенную сумму финансовой ренты:



Находим наращенную сумму финансовой ренты при ставке наращения :



Наращенная стоимость ренты при финансовой ренты постнумерандо к концу четвертого года при ставке 185 составит 150,2238 тыс. руб. А при ставке 21% - 155,9210 тыс. руб. Наращенная стоимость ренты при ставке 21% больше, чем при ставке 18% на 5,6972 руб.

Бланк выполнения задания 6

Условие задания.

Два вклада размером 120 000 руб. размещены на четыре года под 12 % годовых. При этом один вклад помещен под простые проценты, второй – под сложные. В течение этого периода цены на товары и услуги в результате действия инфляции увеличились на 11 %. Рассчитайте размер реально наращенных сумм по каждому из вкладов.
Решение задания:

1. Определите номинально наращенную сумму денег по простым процентам по формуле:

,

где – наращенная сумма ссуды;

– первоначальная сумма долга;

– годовая процентная ставка;

– число лет наращения.

2. Определите номинально наращенную сумму денег по сложным процентам по формуле:

.
3. Определите индекс покупательной способности по формуле:

,

где 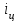– индекс цен (в приведенной задаче равен ).

4. 
   Определите реально наращенные суммы по формулам:
   

5. Сделайте выводы.

Решение:

1. Наращенная сумма вклада по простым процентам составит: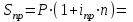

120 000 ∙ (1 + 0,12 ∙ 4) = 177 600 руб.

2. Наращенная сумма вклада по сложным процентам составит: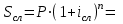

120 000 ∙ (1 + 0,12)⁴ = 188 822,32 руб.

3. Находим индекс покупательной способности денег:



4. Находим реальную наращенную сумму для вклада по простым процентам:

177 600 ∙ 0,9091 = 161 454,55 руб.

5. Находим реальную наращенную сумму для вклада по сложным процентам:

188 822,32 ∙ 0,9091 = 171 656,66 руб.

Реальная наращенная сумма по первому вкладу составит 161 454,55 руб., по второму вкладу – 171 656,66 руб. Реальная наращенная сумма больше первоначальной величины вклада. Финансовые операции прибыльны.