Полная математическая индукция. В основе метода математической индукции лежит

• Название: В основе метода математической индукции лежит
• Дата: 17.06.2019
• Размер: 32.71 Kb.
• Имя файла: Полная математическая индукция.docx
• Тип: Документы; #82119

Полная математическая индукция – умозаключение, базирующееся на общем выводе обо всем классе каких-либо предметов, функционально связанных отношениями натурального ряда чисел на основании знания этой функциональной связи. При этом процесс доказательства проходит в три этапа: на первом доказывается правильность положения математической индукции. Пример: f = 1, это базис индукции; следующий этап строится на предположении о правомерности положения для всех натуральных чисел. То есть, f=h, это предположение индукции; на третьем этапе доказывается справедливость положения для числа f=h+1, на основании верности положения предыдущего пункта – это индукционный переход, или шаг математической индукции. Примером может служить так называемый "принцип домино": если падает первая косточка в ряду (базис), то упадут все косточки в ряду (переход) .

Условие: на плоскости размещено h окружностей. Требуется доказать, что при любом расположении фигур образуемая ими карта может быть правильно раскрашена двумя красками. Решение: при h=1 истинность утверждения очевидна, поэтому доказательство будет строиться для количества окружностей h+1. Примем допущение, что утверждение достоверно для любой карты, а на плоскости задано h+1 окружностей. Удалив из общего количества одну из окружностей, можно получить правильно раскрашенную двумя красками (черной и белой) карту. При восстановлении удаленной окружности меняется цвет каждой области на противоположный (в указанном случае внутри окружности). Получается карта, правильно раскрашенная двумя цветами, что и требовалось доказать.

В основе метода математической индукции лежит принцип математической индукции.

Он заключается в следующем: некоторое утверждение справедливо для всякого натурального n, если

1. 
   оно справедливо для n = 1 и
   
2. 
   из справедливости утверждения для какого-либо произвольного натурального n = k следует его справедливость для n = k+1.
   

То есть, доказательство по методу математической индукции проводится в три этапа:

1. 
   во-первых, проверятся справедливость утверждения для любого натурального числа n (обычно проверку делают для n = 1);
   
2. 
   во-вторых, предполагается справедливость утверждения при любом натуральном n=k;
   
3. 
   в-третьих, доказывается справедливость утверждения для числа n=k+1, отталкиваясь от предположения второго пункта.
   

.

Доказательство.

Метод математической индукции предполагает доказательство в три пункта.

Поехали!

1. 
   Проверим равенство для n = 1. Имеем . Это равенство верное.
   
2. 
   Предположим, что есть справедливая формула.
   
3. 
   Докажем, что отталкиваясь от справедливого равенства из второго пункта.
   

Сумма k+1 первых членов последовательности представляется как сумма первых k членов исходной числовой последовательности и k+1 ого члена:


Так как из второго пункта, то


Осталось привести дроби к общему знаменателю, привести подобные слагаемые, воспользоваться формулой сокращенного умножения квадрат суммы и произвести сокращение: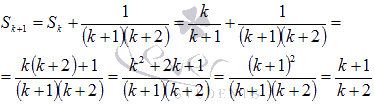


Следовательно, доказано равенство третьего пункта.

Таким образом, выполнены все три шага метода математической индукции и тем самым доказано наше предположение о формуле .