Вариант 3 Задача 1
 Скачать 301.07 Kb. Скачать 301.07 Kb.
|
|
Вариант №3 Задача №1 Два точеных заряда  и и 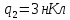 находятся на расстоянии находятся на расстоянии 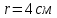 друг от друга. Найти напряженность и потенциал электростатического поля в точке, удаленной от первого заряда на расстояние друг от друга. Найти напряженность и потенциал электростатического поля в точке, удаленной от первого заряда на расстояние  и от второго на и от второго на 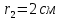 . .Д 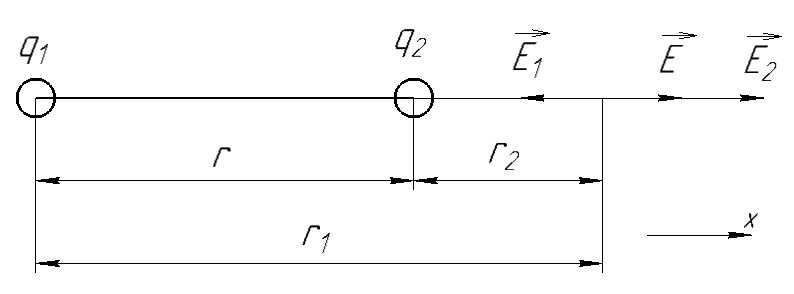 ано: Решение ано: Решение 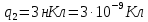 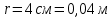 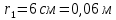  Найти:  Из анализа числовых значений расстояний  получим, что оба заряда и искомая точка лежат на одной прямой (см. рисунок). По определению суммарная напряженность в искомой точке будет равна векторной сумме напряженностей от первого и второго зарядов: получим, что оба заряда и искомая точка лежат на одной прямой (см. рисунок). По определению суммарная напряженность в искомой точке будет равна векторной сумме напряженностей от первого и второго зарядов: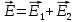 В проекции на ось Ох (см. рисунок) получим,  Найдем напряженности, создаваемые в искомой точке первым и вторым зарядами в отдельности. Напряженность, создаваемая точечным зарядом, определяется по формуле: 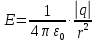 где 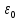 – диэлектрическая постоянная; – диэлектрическая постоянная; – величина точечного заряда; – величина точечного заряда; – расстояние от заряда до искомой точки. – расстояние от заряда до искомой точки.1-й заряд  2-й заряд 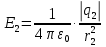 В итоге получим, 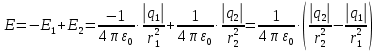 Суммарный потенциал, создаваемый в некоторой точке системой зарядов, определяется как алгебраическая сумма потенциалов, создаваемых в искомой точке каждым из зарядов в отдельности.  В данном случае получим,  Потенциал, создаваемый точечным зарядом, определяется по формуле:  где 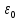 – диэлектрическая постоянная; – диэлектрическая постоянная; – величина точечного заряда; – величина точечного заряда; – расстояние от заряда до искомой точки. – расстояние от заряда до искомой точки.Тогда,  Подставим в полученные формулы числовые значения: 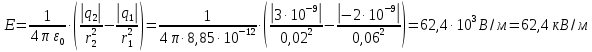 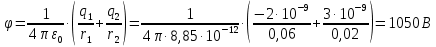 Ответ: 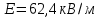 , , 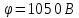 . .Задача №2 К бесконечно протяженной плоскости (поверхностная плотность заряда  ) прикреплена нить, на которой висит шарик (масса ) прикреплена нить, на которой висит шарик (масса  , заряд , заряд  ), заряженный одноименно с плоскостью. Нить с шариком отклонена на угол ), заряженный одноименно с плоскостью. Нить с шариком отклонена на угол  . Определить угол отклонения нити . Определить угол отклонения нити  . .Д  ано: Решение ано: Решение    Найти:  На заряженный шарик действуют сила тяжести  , сила натяжения нити , сила натяжения нити  и сила и сила  со стороны электрического поля, создаваемого заряженной плоскостью. Запишем для шарика второй закон Ньютона: со стороны электрического поля, создаваемого заряженной плоскостью. Запишем для шарика второй закон Ньютона: В проекции на оси Ох и Оу (см. рис.) получим:   В итоге получим следующую систему уравнений. 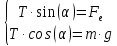 Разделим первое уравнение системы на второе:  Сила, действующая со стороны электрического поля на электрический заряд, определяется по формуле:  где  – величина электрического заряда; – величина электрического заряда;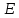 – напряженность электрического поля в точке, в которой расположен электрический заряд. – напряженность электрического поля в точке, в которой расположен электрический заряд.Напряженность электрического поля, создаваемого бесконечной равномерно заряженной плоскостью, вычисляется по формуле: 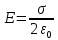 где 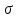 – поверхностная плотность заряда плоскости; – поверхностная плотность заряда плоскости;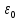 – диэлектрическая постоянная. – диэлектрическая постоянная.Подставим все полученные выше выражения в исходное. 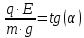  Выразим из полученного соотношения угол  отклонения нити . отклонения нити . Подставим в полученную формулу числовые значения: 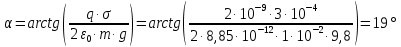 Ответ:  . .Задача №3 Электрическое поле образовано заряженной плоскостью, с поверхностной плотностью заряда 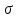 . Электрон перемещается в поле от одной точки пространства (на расстоянии . Электрон перемещается в поле от одной точки пространства (на расстоянии  от плоскости) до другой (на расстоянии от плоскости) до другой (на расстоянии 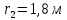 от плоскости), при этом ее скорость изменяется от от плоскости), при этом ее скорость изменяется от  до до  . Найти величину поверхностной плотности заряда . Найти величину поверхностной плотности заряда 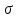 . .Д 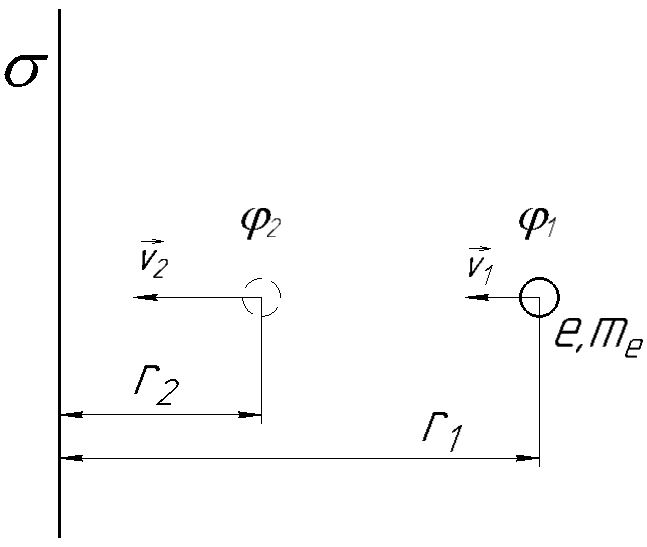 ано: Решение ано: Решение 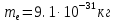     Найти: 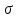 Согласно закону сохранения энергии изменение кинетической энергии электрона равно работе сил электрического поля.  По определению работа сил, совершаемая при перемещении заряда в электрическом поле, вычисляется по формуле:  где  – величина заряда; – величина заряда;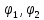 – потенциалы начальной и конечной точек, соответственно. – потенциалы начальной и конечной точек, соответственно.Потенциал, создаваемый бесконечной равномерно заряженной плоскостью на расстоянии  от плоскости, определяется по формуле: от плоскости, определяется по формуле: где 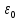 – диэлектрическая постоянная; – диэлектрическая постоянная;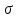 – поверхностная плотность заряда плоскости. – поверхностная плотность заряда плоскости.По определению кинетическая энергия тела определяется по формуле:  где 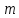 – масса тела; – масса тела;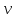 – скорость движения тела. – скорость движения тела.Подставим все полученные выше формулы в исходную.  Выразим искомую величину поверхностной плотности заряда 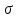 . .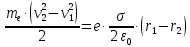  Подставим в полученную формулу числовые значения:  Ответ:  . .Задача №4 Найти значение и направление тока через резистор  . Внутренние сопротивления бесконечно малы. Параметры цепи . Внутренние сопротивления бесконечно малы. Параметры цепи  , ,  , , 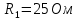 , ,  . .Д  ано: Решение ано: Решение   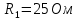  Найти:  Для определения токов в ветвях цепи запишем первый и второй законы Кирхгофа. Первый закон Кирхгофа (для правого узла схемы):  Второй закон Кирхгофа (для большого контура):  Второй закон Кирхгофа (для нижнего контура):  Получим итоговую систему трех уравнений:  Решим данную систему относительно искомой силы тока  . .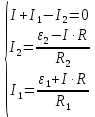  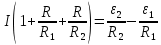  Подставим в полученную формулу числовые значения: 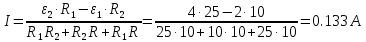 Поскольку вычисленное значение силы тока положительное, то направление силы тока соответствует направлению, указанному на рисунке. Ответ: 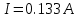 . .Задача №5 По двум прямолинейным бесконечно длинным проводникам текут токи  и и  в одном направлении. Проводники параллельны друг другу и расстояние между ними в одном направлении. Проводники параллельны друг другу и расстояние между ними  . Найти значение вектора магнитной индукции в точке, находящейся на расстоянии . Найти значение вектора магнитной индукции в точке, находящейся на расстоянии  от первого проводника и от первого проводника и 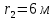 от второго. от второго.Дано: Решение      Найти:  По условию указано, что требуется найти величину вектора магнитной индукции в точке, удаленной на расстоянии  от первого и второго проводников соответственно. Следовательно, на указанных трех точках (если рассматривать плоскость, перпендикулярную проводникам) можно построить треугольник со сторонами от первого и второго проводников соответственно. Следовательно, на указанных трех точках (если рассматривать плоскость, перпендикулярную проводникам) можно построить треугольник со сторонами  . Для указанных по условию расстояний неравенство треугольника – длина любой стороны треугольника всегда меньше или равна сумме длин двух его других сторон – вырождается в равенство. . Для указанных по условию расстояний неравенство треугольника – длина любой стороны треугольника всегда меньше или равна сумме длин двух его других сторон – вырождается в равенство. Следовательно, треугольник вырождается в прямую линию. На рисунке представлена схема для данных условий.  Согласно принципу суперпозиции, суммарная индукция в искомой точке будет равна векторной сумме магнитных индукций, создаваемых в данной точке первым и вторым проводниками с током.  Длинный прямой проводник с током создает вокруг себя круговое магнитное поле. Величина индукции поля в некоторой точке, удаленной от проводника на расстояние  , определяется по формуле: , определяется по формуле: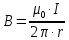 где  – величина тока в проводнике; – величина тока в проводнике; – расстояние до точки, в которой определяется магнитная индукция; – расстояние до точки, в которой определяется магнитная индукция; – магнитная постоянная. – магнитная постоянная.Тогда получим,  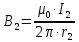 В данном случае вектора магнитных индукций первого и второго проводника сонаправлены (см. рис). Тогда величина вектора суммарной магнитной индукции будет равна:  Подставим в полученную формулу числовые значения: 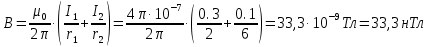 Ответ:  . .Задача №6 Электрон влетает в плоский горизонтальный конденсатор параллельно его пластинам со скоростью  . Длина конденсатора . Длина конденсатора  . Напряженность электрического поля конденсатора . Напряженность электрического поля конденсатора  . При вылете из конденсатора электрон попадает в магнитное поле с индукцией . При вылете из конденсатора электрон попадает в магнитное поле с индукцией  , перпендикулярное электрическому и параллельное начальной скорости влета электрона в конденсатор. Электрон в магнитном поле начинает двигаться по винтовой линии радиусом , перпендикулярное электрическому и параллельное начальной скорости влета электрона в конденсатор. Электрон в магнитном поле начинает двигаться по винтовой линии радиусом  и шагом и шагом  . Определить . Определить  . .Дано: Решение        Найти:  При пролете через конденсатор на электрон действует сила Кулона, которая отклоняет электрон от первоначального направления. Запишем второй закон Ньютона:    где  – электрический заряд электрона; – электрический заряд электрона; – напряженность электрического поля в конденсаторе; – напряженность электрического поля в конденсаторе; – масса электрона. – масса электрона.В начальный момент времени электрон имел только продольную составляющую скорости (вдоль оси  ). Следовательно, движение электрона вдоль оси ). Следовательно, движение электрона вдоль оси  – равноускоренное движение без начальной скорости. Тогда скорость электрона можно рассчитать по формуле: – равноускоренное движение без начальной скорости. Тогда скорость электрона можно рассчитать по формуле: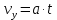 где  – время пролета электрона через конденсатор; – время пролета электрона через конденсатор;Время пролета электрона через конденсатор равно:  Тогда,  На электрон, движущийся в магнитном поле, действует сила Лоренца  , которая придает электрону центростремительное ускорение , которая придает электрону центростремительное ускорение  . Запишем для электрона второй закон Ньютона: . Запишем для электрона второй закон Ньютона: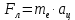  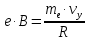 Тогда радиус винтовой линии будет равен.  Период обращения электрона по винтовой линии равен:  С другой стороны, за один период электрон проходит вдоль оси 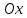 расстояние расстояние  : : Выразим из полученных выше соотношений искомые величины начальной скорости электрона  и длины конденсатора и длины конденсатора  . .  Подставим в полученные формулы числовые значения: 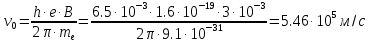 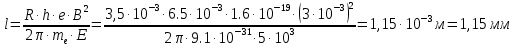 Ответ:  , ,  . .Задача №7 В магнитном поле, индукция которого  , вращается стержень длиной , вращается стержень длиной  с угловой скоростью с угловой скоростью  . Ось вращения проходит через конец стержня и параллельна магнитному полю. При этом на концах стержня возникает ЭДС индукции . Ось вращения проходит через конец стержня и параллельна магнитному полю. При этом на концах стержня возникает ЭДС индукции 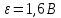 . Найти индукцию магнитного поля . Найти индукцию магнитного поля  . .Д  ано: Решение ано: Решение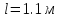   Найти:  Запишем закон электромагнитной индукции Фарадея:  где  – изменение магнитного потока через контур. – изменение магнитного потока через контур.В данном случае за один оборот стержень пересекает магнитный поток, равный: 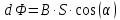 где  – величина индукции магнитного поля; – величина индукции магнитного поля; – площадь контура; – площадь контура; – угол между вектором индукции и нормалью к плоскости контура. – угол между вектором индукции и нормалью к плоскости контура.В данном случае площадь контура – площадь круга, радиуса, равного длине стержня  : : По условию указано, что плоскость вращения перпендикулярна силовым линиям поля. Тогда,  Поскольку рассчитывается изменение магнитного потока для одного оборота, то промежуток времени равен периоду вращения:  Угловая скорость вращения связана с периодом вращения соотношением:  Подставим полученные формулы в исходную. Выразим величину индукции магнитного поля:   Подставим в полученную формулу числовые значения:  Ответ:  . . |
