|
|
методика. Вариант 9 Задание 1
Вариант 9
Задание 1.
Число - одно из основных понятий математики, возникшее впервые в связи с потребностями счета предметов. Построение системы целых неотрицательных чисел на основе теории множеств связано с именем Г. Кантора. В этой теории, которую называют количественной теорией, основополагающими являются понятия конечного множества и взаимно однозначного соответствия.
С теоретико-множественных позиций натуральное число рассматривается как число элементов конечного множества. Число 0 тоже имеет теоретико-множественное истолкование: оно соответствует пустому множеству . Так как одному и тому же множеству соответствует только одно число, то вся совокупность конечных множеств распадается на классы равночисленных (эквивалентных) множеств. Поэтому натуральным числом называют общее свойство класса непустых эквивалентных множеств.
Так, число 5 - то общее свойство, которым обладают множества, содержащее пять пальцев, пять вершин пятиконечной звезды, пять сторон пятиугольника и т.п. Каждый класс определяется любым своим представителем, например, отрезком натурального ряда.
Два натуральных числа называются равными, если соответствующие им множества эквивалентны, в противном случае - числа называются неравными.
Отношение равенства целых неотрицательных чисел обладает следующими свойствами:
1. Рефлексивность. Любое целое неотрицательное число равно самому себе, т.е. а = а.
2. Симметричность. Если число а равно числу в, то и число в равно числу а, т.е. если
а = b, то b = а.
3. Транзитивность. Два числа, равные третьему, равны между собой, т.е. если
а = b и b = с, то а = с.
Отношение "меньше" тоже имеет теоретико-множественное истолкование. Если множество А равномощно собственному подмножеству множества В и n(A)=a, n(B)=b , говорят, что число а меньше числа b, и пишут а < b. В этой же ситуации говорят, что b больше а, и пишут b > а.
Отношение "меньше" на множестве Z₀ обладает следующими свойствами:
1. Для любого отличного от нуля числа а справедливо неравенство 0 < а.
2. Антирефлексивность. Любое целое неотрицательное число не вступает в отношение "меньше" с самим собой, т.е. неверно, что а < а
3. Асимметричность. Если а < b, то неверно, что b < а.
4. Транзитивность. Если а < b, b < с, то а < с.
Для любых целых неотрицательных чисел а, d и с справедливы следующие законы арифметических операций:
1. Коммутативности: а + b = b+ а, а b = b b = b а. а.
2. Ассоциативности: (а + в) + с = а + (b + с), (а b) b) с = а с = а (b (b с). с).
3. Дистрибутивности:
Правый и левый дистрибутивные законы умножения относительно сложения:
(а + b)с = ас + bс; с(а + b) = са + сb;
Правый и левый дистрибутивные законы умножения относительно вычитания: (а - b)с = ас - bс; с(а - b) = са - сb.
Объединение 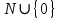 называют множеством целых чисел и обозначают символом Z называют множеством целых чисел и обозначают символом Z
.
Задание 2. Не выполняя деление уголком, найдите наиболее рациональным способом частное, выбранный способ обоснуйте: 765: 45; 765:9.
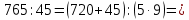
Так как от перестановки множителей произведение не изменится, то множители можно поменять местами
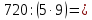 16 16
Сначала разделим 720 на 9
720:9=80
а теперь полученное частное разделим на 5
80:5=16.
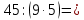
Сначала разделим 45 на 9
45:9=5
а теперь полученное частное разделим на 5
5:5=1.
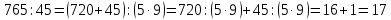
765:9
765:9=(720+45):9=720:9+45:9=80+5=85
Чтобы разделить какое-нибудь число на произведение, можно разделить это число на первый сомножитель, полученное частное на второй сомножитель, это частное на третий и т.д.
Чтобы разделить сумму на число, нужно каждое слагаемое разделить на число и сложить полученные частные.
Использовали распределительные свойства деления
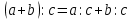

Задание 3. Одно число на 38 больше другого. При делении одного из них на другое с остатком в частном получается 2 и в остатке 3. Найдите эти числа.
Решение.
Обозначим первое число через а, тогда второе число обозначим через а+38.
Получаем
а+38=2*а+3
Решаем полученное уравнение
2а-а=38-3
а=35
Тогда другое число больше на 38 и равно
35+38=73
Ответ: 35 и 73
Задание 4. Исходя из различных определений отношения, объясните, почему 2 < 9.
Число 2 меньше числа 9 тому что при счете число 2 называют раньше числа 9
Отрезок длины 2 меньше отрезка длины 9
Пусть 2=n(A) и 9=n(B) . Во множестве В можно выделить собственное подмножество В1, равномощное множеству А.
2<9  A A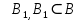
Возьмем множество А, содержащее 2 элемента и множество В, содержащее 9 элементов, т.е. n(А) = 2, n(B) = 9. Например, А = {a, b}, B = {c, d, e, f, r,l,m,n,k}. Из множества B можно выделить подмножество В , равномощное множеству А: например В ={m, n} и АВ . Согласно определению отношения «меньше», 2<9
Задание 5. Дайте теоретико-множественное истолкование суммы k слагаемых и, используя теоретико-множественный смысл суммы, объясните решение задачи:
С теоретико- множественного истолкования сумма к слагаемых это число элементов в объединении к множеств, т.е.
Дима сорвал 4 груши, Нина – 7. Сколько всего груш сорвали Дима и Нина вместе?
В задаче рассматриваются три множества: множество А груш Димы, множество В груш Нины и их объединение.
Требуется узнать число элементов в этом объединении, а оно находится сложением. Так n(А) = 4, n(В) = 7 и  . .
Сумма 4+7 – это математическая модель данной задачи. Вычислив значение этого выражения, получим ответ на вопрос задачи: 4+7=11. Следовательно, Дима и Нина собрали 11 груш.
Задание 6. Используя метод математической индукции, докажите, что для любого натурального числа n истины утверждения: 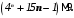
Решение.
Используем метод математической индукции
Проверим для n= 1: 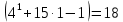 18 делится на 9 18 делится на 9
Допустим, что утверждение верно для n=k.
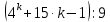
Для n=k выражение примет вид
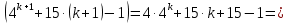

=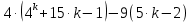
Так как
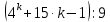
То 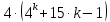 делится на 9. делится на 9.
Так как  делится на 9, то делится на 9, то
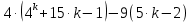 делится на 9 делится на 9
Утверждение верно для n= 1 . Если утверждение верно для n=k, то оно верно и для n=k+1. Тогда утверждение верно для любого натурального числа n. Что и требовалось доказать. |
|
|
 Скачать 26.22 Kb.
Скачать 26.22 Kb.