Векторы на плоскости и в пространстве.(1). Векторы и действия над ними Вектор

• Название: Векторы и действия над ними Вектор
• Дата: 26.10.2021
• Размер: 226.21 Kb.
• Имя файла: Векторы на плоскости и в пространстве.(1).docx
• Тип: Документы; #256459

Векторы и действия над ними

Вектор – это направленный прямолинейный отрезок, то есть отрезок, имеющий определенную длину и определенное направление. Пусть точка  А – начало вектора, а точка B – его конец, тогда вектор обозначается символом   или  .

Вектор   называется противоположным вектору   и может быть обозначен  .

Сформулируем ряд базовых определений.

Длиной или модулем вектора   называется длина отрезка и обозначается  . Вектор нулевой длины (его суть - точка) называется нулевым   и направления не имеет.

Вектор   единичной длины, называется единичным. Единичный вектор,  направление которого совпадает с направлением вектора  , называется ортом вектора   .

Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых, записывают . Коллинеарные векторы могут иметь совпадающие или противоположные направления. Нулевой вектор считают коллинеарным любому вектору.

Векторы называются равными  , если они коллинеарны, одинаково направлены и имеют одинаковые длины.

 Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или на параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.

Рассмотрим в пространстве прямоугольную систему координат 0xyz. Выделим на осях координат 0x, 0y, 0z единичные векторы (орты) и обозначим их через   соответственно. Выберем произвольный вектор  пространства и совместим его начало с началом координат. Спроектируем вектор  на координатные оси и обозначим проекции через a_x, a_y, a_z  соответственно. Тогда нетрудно показать, что 

.                                     (2.25)

Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа a_x, a_y, a_z называются координатами вектора . Таким образом, координаты вектора являются его проекциями на оси координат. Векторное равенство (2.25) часто записывают в виде 

.

С использованием формулы длины отрезка, известной из школьной геометрии, можно найти выражение для вычисления модуля вектора  :

   , то есть модуль вектора равен корню квадратному из суммы квадратов его координат.

Обозначим углы между вектором   и осями координат через α, β, γ  соответственно. Косинусы этих углов называются для вектора   направляющими, и для них выполняется соотношение: Верность данного равенства можно показать с помощью свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем пункте 4.

Пусть в трехмерном пространстве заданы векторы   своими координатами.  Имеют место следующие операции над ними: линейные (сложение, вычитание, умножение на число и проектирование вектора на ось или другой вектор); не линейные – различные произведения векторов (скалярное, векторное, смешанное).

1. Сложение  двух векторов производится покоординатно, то есть если 

.

Данная формула имеет место для произвольного конечного числа слагаемых.

Геометрически два вектора складываются по двум правилам:

а) правилотреугольника – результирующий вектор суммы двух векторов соединяет начало первого из них с концом второго при условии, что начало второго совпадает с концом первого вектора; для суммы векторов – результирующий вектор суммы соединяет начало первого из них с концом последнего вектора-слагаемого при условии, что начало последующего слагаемого совпадает с концом предыдущего;

б) правилопараллелограмма (для двух векторов) – параллелограмм строится на векторах-слагаемых как на сторонах, приведенных к одному началу; диагональ параллелограмма исходящая из  их общего начала, является  суммой  векторов.

2. Вычитание двух векторов производится покоординатно, аналогично сложению, то есть если  , то

.

Геометрически два вектора складываются по уже упомянутому правилу параллелограмма  с учетом того, что разностью векторов является диагональ, соединяющая концы векторов, причем результирующий вектор направлен из конца вычитаемого в конец уменьшаемого вектора.

Важным следствием вычитания векторов является тот факт, что если известны координаты начала и конца вектора, то для вычисления координат вектора необходимо из координат его конца вычесть координаты его начала. Действительно, любой вектор пространства   может быть представлен в виде разности двух векторов, исходящих из начала координат:  . Координаты векторов  и  совпадают с координатами точек А и В, так как начало координат О(0;0;0). Таким образом, по правилу вычитания векторов следует произвести вычитание координат точки А из координат точки В.

3. Умножение вектора на число λ покоординатно: .

При  λ>0 – вектор  сонаправлен  ; λ<0 – вектор   противоположно направлен  ; |λ|>1 –  длина вектора   увеличивается в λ раз; |λ|<1 –  длина вектора    уменьшается в λ раз.

4. Пусть в пространстве задана направленная прямая (ось l), вектор   задан координатами конца и начала. Обозначим проекции точек A и B на ось l соответственно через A’  и B’.

Проекцией  вектора   на ось l называется длина вектора  ,   взятая со знаком «+», если вектор   и ось  l  сонаправлены,  и  со знаком «–»,  если   и l  противоположно направлены. 

Если в качестве оси l взять некоторый другой вектор  , то получим проекцию вектора   на вектор  .

Рассмотрим некоторые основные свойства проекций:

1)     проекция вектора   на ось l равна произведению модуля вектора   на косинус угла  между вектором и осью, то есть  ;

2.)     проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой; 

3)     проекция суммы нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.

Сформулируем определения и теоремы о произведениях векторов, представляющих нелинейные операции над векторами.

5. Скалярным произведением   векторов   и   называется число (скаляр), равное произведению длин этих векторов на  косинус угла φ между ними, то есть 

                                                                                                                                                                    

Очевидно, что скалярный квадрат любого ненулевого вектора равен квадрату его длины, так как в этом случае угол  , поэтому его косинус (в 2.27) равен 1.

Теорема 2.2. Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения 

Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть 

Теорема 2.3. Скалярное произведение двух векторов  , заданных своими координатами, равно сумме  произведений их одноименных координат, то есть 

                                                                                                                                                       (2.28)

С помощью скалярного произведения векторов можно вычислить угол между ними.  Если  заданы два ненулевых вектора своими координатами  , то косинус угла φ между ними:

                                                                                                                                            (2.29)

Отсюда следует условие перпендикулярности ненулевых векторов    и   :

                  

                                                                                                                                                                              (2.30)

Нахождение проекции вектора   на направление, заданное вектором   , может осуществляться по формуле

                                                                                                                       (2.31)

С помощью скалярного произведения векторов находят работу постоянной  силы   на прямолинейном участке пути.

Предположим, что под действием постоянной силы   материальная точка перемещается прямолинейно из положения А в положение B. Вектор силы  образует угол φ с вектором перемещения   (рис. 2.14). Физика утверждает, что работа силы   при перемещении    равна  .



Следовательно, работа постоянной силы при прямолинейном перемещении точки ее приложения равна скалярному произведению вектора силы на вектор перемещения.

       Пример 2.9. С помощью скалярного произведения векторов найти угол при вершине A параллелограмма  ABCD,  построенного на векторах     

     

Решение. Вычислим модули векторов и их скалярное произведение по теореме (2.3):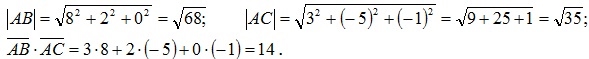



Отсюда согласно формуле (2.29) получим косинус искомого угла 


Задание: Выполните проверочные тесты

https://onlinetestpad.com/ru/test/158941-vektory-v-prostranstve

https://videouroki.net/tests/3979393/