Вопросы для самоконтроля раздел 2 Степаненко А.А. ЭНМ-120807. Вопросы для самоконтроля Как рассчитывается величина теплового потока на границе области Почему при выполнении расчета необходима информация о поле потенциала переноса во всей области
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
Вопросы для самоконтроля Как рассчитывается величина теплового потока на границе области? Почему при выполнении расчета необходима информация о поле потенциала переноса во всей области? Нагрев полуограниченного массива, 0 x , с нулевой начальной температурой. Температура поверхности - заданная функция времени T (t) S . Определить величину теплового потока на поверхности q (t) S . Математическая модель формулируется следующим образом. 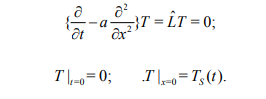 Представим Lˆ — линейный дифференциальный оператор в виде разложения на множители в операторной форме, используя тривиальную формулу разности квадратов двух величин. Справедливость такого представления опирается на рассмотренные выше свойства операции дробного дифференцирования и линейность соответствующих операторов дифференцирования по координатам. Исходное уравнение при этом приобретает следующую форму 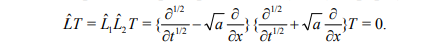 Уравнение удовлетворяется приравниванием нулю результатов применения к искомой функции любого из операторов - левого или правого в силу перестановочности этих операций. Однако применение левого оператора приведет к положительному знаку производной T/x , что противоречит условиям поставленной задачи. Отсюда в дальнейшем рассматривается только правое соотношение Таким образом, тепловой поток на границе с учетом граничного условия задачи (14) ( граничное условие I рода) рассчитывается непосредственно по заданной температуре на поверхности: В случае задания на поверхности массива величины теплового потока (граничное условие II рода) температура на поверхности T (t) S находится из действием на обе части равенства оператором D1/2 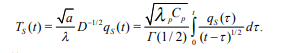 Если полуограниченный массив прогревается за счет подвода тепла конвекцией от среды с заданной температурой T (t) cp с эффективностью = const ( граничное условие III рода), тепловой поток qs на поверхности массива находится подстановкой в предыдущее выражение: Операторное уравнение решается путем применения к левой и правой части обратного оператора, явное выражение для которого получено путем формального разложения в биномиальный ряд: 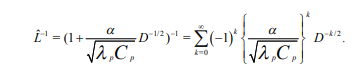 Таким образом, величина теплового потока на границе в случае граничных условий III рода определяется выражением: 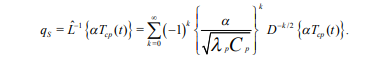 Температуру на поверхности области можно найти по найденному значению теплового потока, используя выражение : 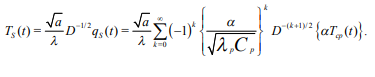 Как реализуется операторное разложение исходного уравнения теплопроводности? Насколько справедливо такое представление? Операторное уравнение решается путем применения к левой и правой части обратного оператора, явное выражение для которого получено путем формального разложения в биномиальный ряд: 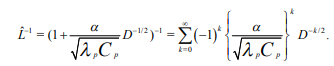 Таким образом, величина теплового потока на границе в случае граничных условий III рода определяется выражением: 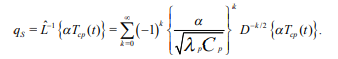 Температуру на поверхности области можно найти по найденному значению теплового потока, используя выражение: 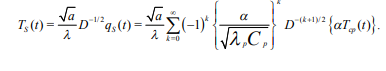 Почему в качестве основы для дальнейших расчетов выбирается правый сомножитель операторного разложения? Уравнение удовлетворяется приравниванием нулю результатов применения к искомой функции любого из операторов - левого или правого в силу перестановочности этих операций. Однако применение левого оператора приведет к положительному знаку производной T/x , что противоречит условиям поставленной задачи. Отсюда в дальнейшем рассматривается только правое соотношение 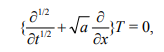 решение которого обращает уравнение исходной задачи в тождество. Из (15) определяется связь производной потенциала переноса тепла с величиной потенциала в любой точке рассматриваемой области, в том числе на ее границе при x = 0 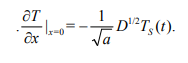 Как связаны операции интегрального преобразования Лапласа и дробного дифференцирования порядка γ = –1/2? Определение материальных и энергетических потоков на границе раздела сред - одна из основных задач теории тепломассообмена. В прикладном плане такие задачи встречаются значительно чаще задач расчета полей потенциалов переноса (температуры, концентрации) в области. В классике расчет величин потенциалов и потоков на поверхности производится после реконструкции полей потенциалов во всей области, что выливается в предварительное решение сложных задач, затрудняющих достижение поставленной цели. Бесполевые методы определения потоков основаны на применении операций дробного дифференцирования [1], [2]. Освоение математического аппарата дробного дифференцирования требует предварительного ознакомления с операционным исчислением (интегральным преобразованием Лапласа) [4], [6] и некоторыми специальными функциями. Представляемые методы особенно эффективны при рассмотрении задач в полуограниченных пространственных областях. Отдельные примеры применения методов дробного дифференцирования в ограниченных пространственных областях представлены в [1], [2]. Это обстоятельство не снижает значения представляющихся возможностей, поскольку получаемые аналитические конструкции могут использоваться как асимптотические результаты при отладке и тестировании программ реализации сложных задач или поисков оптимальных решений. Операцию дифференцирования функций можно обобщить на показатели произвольного порядка с помощью введения дробных производных Римана - Лиувилля - Летникова [1]-[3]: 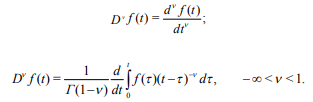 Модификация выражения (2.1) осуществляется путем выполнения дифференцирования по параметру t : 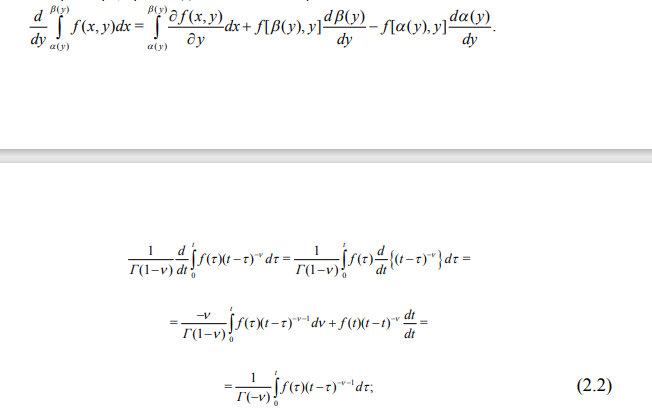 здесь использовано рекуррентное соотношение для Г-функции Рассмотрите случай прогрева полуограниченной области с нулевой начальной температурой. На границе области с начального момента времени поддерживается температура Найдите тепловой поток на границе, используя аппарат дробного дифференцирования.   Рассмотрите случай прогрева полуограниченной области с нулевой начальной температурой. На границу области с начального момента времени подводится тепловой поток плотностью Найдите температуру на границе, используя аппарат дробного дифференцирования.  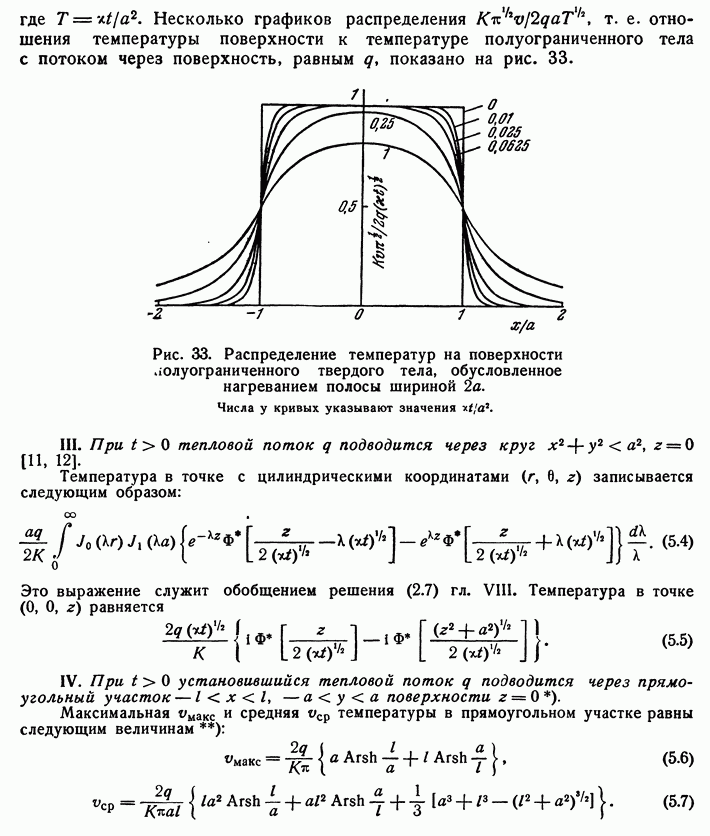 Рассмотрите случай прогрева полуограниченной области с нулевой начальной температурой. На границе области с начального момента времени происходит конвективный теплообмен с интенсивностью.    |
