лекция 1 ОАиП Введение в теорию алгоритмов ИС для эор. Введение в теорию алгоритмов
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
|
09.02.07 – Основы алгоритмизации и программирования - Лекция 1 ТЕМА: Введение в теорию алгоритмов. Литература: 1. http://inf1.info/algorithmterm – Лекции по теории алгоритмов. 2. Семакин И.Г., Шестаков А.П. Основы программирования. 3. Ильиных А.П. Теория алгоритмов: учебное пособие Понятие алгоритма Сначала определение понятия алгоритма было проблемой математики и представляла собой поиск способов решения задач определенного типа посредством определенного набора указаний. Однако с течением времени теория алгоритмов стала развиваться за счет влияния открытий не только в математике, но и в информатике. В 40-х годах появление ЭВМ способствовало развитию теории алгоритмов, вызвало к жизни разделы этой теории, имеющие ярко выраженную прикладную направленность. Это прежде всего алгоритмические системы и алгоритмические языки, являющиеся основой современной теории программирования для универсальных ЭВМ, и способы точного описания отображений, реализуемых цифровыми автоматами. В настоящее время алгоритм является одним из главных понятий информатики. Наконец, теория алгоритмов оказалась тесно связанной и с рядом областей лингвистики, экономики, физиологии мозга и психологии, философии, естествознания. Чтобы иметь возможность более уверенно решать алгоритмические задачи, возникающие в различных отделах теоретической и прикладной математики, необходимо иметь достаточно развитую теорию алгоритмов. В настоящее время такая теория алгоритмов уже создана. Изучение этой теории и является целью данного курса. Классическая теория алгоритмов изучает проблемы формулировки задач в терминах формальных языков, вводит понятие задачи разрешения, проводит классификацию задач по классам сложности. Происхождение самого термина «алгоритм» связано с математикой. Это слово происходит от Algorithmi – латинского написания имени Мухаммеда аль- Хорезми (787 – 850), выдающегося математика средневекового Востока. В XII в. был выполнен латинский перевод его математического трактата, из которого европейцы узнали о десятичной позиционной системе счисления и правилах арифметики многозначных чисел. Именно эти правила в то время называли алгоритмами. Сложение, вычитание, умножение столбиком, деление уголком многозначных чисел – это первые алгоритмы в математике. Правила алгебраических преобразований, способы вычислений корней уравнений также можно отнести к математическим алгоритмам. В информатике рассматривается алгоритм обхода вершин графа и т.д. Сегодня слово «алгоритм» настолько широко распространено, что большинству интуитивно понятно. Под ним мы понимаем какую-либо последовательность шагов для достижения той или иной цели.  Однако для теоретической науки понятие «алгоритма» достаточно сложное. Считается, что однозначного определения алгоритма нет, хотя в основном различные источники дают очень близкие определения. Определение: Алгоритм – это последовательность команд управления каким-либо исполнителем. В школьном курсе информатики с понятием алгоритма, с методами построения алгоритмов Вы знакомились на примерах учебных исполнителей: Робота, Черепахи, Чертежника и т.д. Эти исполнители ничего не вычисляют. Они создают рисунки на экране, перемещаются в лабиринтах, перетаскивают предметы с места на место. Таких исполнителей принято называть исполнителями, работающими в обстановке. В разделе информатики под названием «Программирование» изучаются методы программного управления работой ЭВМ. Следовательно, в качестве исполнителя выступает компьютер. Компьютер работает с величинами – различными информационными объектами: числами, символами, кодами и т.п. Поэтому алгоритмы, предназначенные для управления компьютером, принято называть алгоритмами работы с величинами. Рассмотрим неформальное определение понятия алгоритма. Это определение не является строгим математическим определением, а является лишь разъяснением понятия на интуитивном уровне. Определение: Алгоритм – это точное предписание, которое задает вычислительную процедуру. Данная процедура перерабатывает исходный набор данных P (входной объект) и направлена на получение обусловленного этими данными результата Q (объекта на выходе). Данная процедура состоит из отдельных, элементарных шагов – тактов работы алгоритма. Каждый шаг заключается в смене одного набора данных другим набором (объектом, состоянием). Переход от предыдущего состояния к последующему происходит по заранее заданному, конечному набору инструкций. Эти инструкции не должны предполагать никаких догадок и вероятностных соображений со стороны человека или машины, нужно только точно их исполнять. Некоторые состояния опознаются как заключительные, при которых процесс вычислений заканчивается. При этом на основе некоторой инструкции определяется, что считать результатом вычислений. Пусть алгоритм A имеет исходный набор данных P. Возможны следующие три случая протекания алгоритмического процесса. На некотором шаге возникает состояние, опознаваемое как заключительное. При этом происходит остановка вычислений и выдается результат Q. Каждое очередное состояние сменяется последующим до бесконечности, т.е. процесс вычислений никогда не останавливается. При некотором состоянии возникает ситуация, когда процесс вычислений обрывается без выдачи результата (например, не срабатывает инструкция для определения результата вычислений). Тем самым нет перехода к следующему шагу и нет результата вычислений. В этом случае говорим, что произошла безрезультатная остановка. Считается, что алгоритм A применим к исходному набору данных P тогда и только тогда, когда выполнен случай 1, т.е. когда процесс вычислений заканчивается и получен результат вычислений Q. Этот результат будем обозначать через A(P). В случаях 2 и 3 результат A(P) не существует. Исполнитель и разработчик алгоритма Разрабатывать, придумывать алгоритмы могут только разумные существа (например, человек). Исполнитель алгоритма способен выполнять команды, заданные алгоритмом. Животные и человек как исполнители отличаются тем, что могут понимать команды в различных вариантах, одни и те же команды выполнять по-разному, отказаться исполнять команду. Поэтому их называют неформальными исполнителями. Формальный исполнитель может не понимать смысла алгоритма, но все равно правильно выполнить его и получить нужный результат. Формальный исполнитель алгоритма выполняет в строгой последовательности все предписанные алгоритмом команды, не вникая в содержание поставленной задачи, не задумываясь о ее цели, результате и необходимости. Формальный исполнитель не привносит в алгоритм ничего нового и не отбрасывает никаких действий. К формальным исполнителям относят автоматы, роботы и другие технические устройства, исполняющие инструкции (алгоритмы). Однако машины понимают лишь ограниченное число команд и могут обрабатывать данные (объекты) далеко не всех типов. Отсюда следует, что разработчик алгоритма в конечном итоге должен описать алгоритм в допустимых командах определенного исполнителя (той машины, которой будет поручено выполнение алгоритма). Совокупность команд, которые данный исполнитель может выполнять, называется системой команд исполнителя. Объекты (данные) и связи между ними, над которыми исполнитель может выполнять действия, формируют среду исполнителя. Например, исполнитель Робот обитает на клеточном поле. Расположение стен и закрашенных клеток, положение самого Робота задают конкретное состояние среды. Язык, используемый для записи алгоритмов и понятный исполнителю алгоритма, называют алгоритмическим. Существуют словесный способ записи алгоритма (на естественном языке), язык блок-схем, учебный алгоритмический язык и языки программирования. Компьютер является достаточно универсальным исполнителем. С его помощью можно выполнять разнообразные по видам алгоритмы: делать математические вычисления, обрабатывать текстовые данные, изменять графику и др. В каком-то смысле компьютер может делать многое, что и человек, а некоторые вещи намного быстрее. Однако человек и компьютер «разговаривают» на совершенно разных языках: один – на естественном (русском, английском и др.), а другой – на формальном (машинном) языке. Разработав алгоритм, человек должен как-то «объяснить» его компьютеру. Для этих целей служат языки программирования, а результатом записи алгоритма на них является программа. В настоящее время язык программирования – это скорее некий посредник между человеком и вычислительной машиной. Программа, написанная на языке программирования, впоследствии переводится на машинный язык транслятором. Свойства алгоритма Дискретность (в данном случае, разделенность на части) и упорядоченность. Алгоритм должен состоять из отдельных действий (тактов, команд), которые выполняются последовательно друг за другом. Каждое действие начинает выполняться только после завершения выполнения предыдущего действия. Каждый такт является сменой одного набора данных другим набором. Детерминированность (однозначная определенность). Многократное применение одного алгоритма к одному и тому же набору исходных данных всегда дает один и тот же результат. Формальность. Алгоритм не должен допускать неоднозначности толкования действий для исполнителя. Необходимо знать, какие команды исполнителю известны, а какие нет. Полный список команд, которые может выполнить исполнитель, называется системой команд исполнителя. При составлении алгоритма для определенного исполнителя можно использовать лишь те команды, которые имеются в его системе команд. Результативность и конечность. Работа алгоритма должна завершаться за определенное число шагов, при этом задача должна быть решена. Массовость. Определенный алгоритм должен быть применим ко всем однотипным задачам.  Формы записи алгоритма Основные формы записи алгоритма: словесная, на естественном языке; графическая, например, в виде блок-схем; на алгоритмическом языке (псевдокоде). Самым простым способом является словесная запись алгоритма на естественном языке. Если формальным исполнителем алгоритма является человек, то запись алгоритма естественным языком может быть приемлема. Но при изложении алгоритма на естественном языке появляется опасность неточного понимания команд исполнителем, то есть нарушается свойство формальности. Если речь идет о формальном исполнителе, например, роботе или автомате, то естественного языка он может не понимать вовсе. Как бы ни был записан алгоритм: на языке формального исполнителя, на естественном языке или при помощи блок-схемы – он составляется с использованием базовых (основных) алгоритмических структур (конструкций). Задача: На естественном языке составить алгоритм, с помощью которого можно рассчитать площадь прямоугольника, если известны его стороны а и b. Решение: 1) Ввести в компьютер значение стороны а; 2) Ввести значение стороны b прямоугольника; 3) Рассчитать площадь по формуле S = a*b; 4) Вывести на экран компьютера значение площади прямоугольника S. Запись алгоритма в виде блок-схем На языке блок-схем каждый шаг алгоритма описывается с помощью соответствующей фигуры, а последовательность выполнения шагов определяется линиями-связями. Каждая базовая структура должна иметь один вход и один выход. Блок схемы читаются сверху вниз и слева направо. Блок-схемы полезны тем, что обеспечивают легкую «читаемость» алгоритма. Однако это не всегда так: стоит попытаться нарисовать блок-схему для более-менее сложного алгоритма, как она разрастается до невероятных размеров и теряет все свое наглядное преимущество. Поэтому блок-схемы хороши в структурном программировании для описания коротких алгоритмов. Для графического представления алгоритмов в виде блок-схем используются стандартные обозначения элементов (ГОСТ 19.701-90). Ниже приведены основные виды блоков, которые мы будем использовать. Обозначения элементов блок-схем 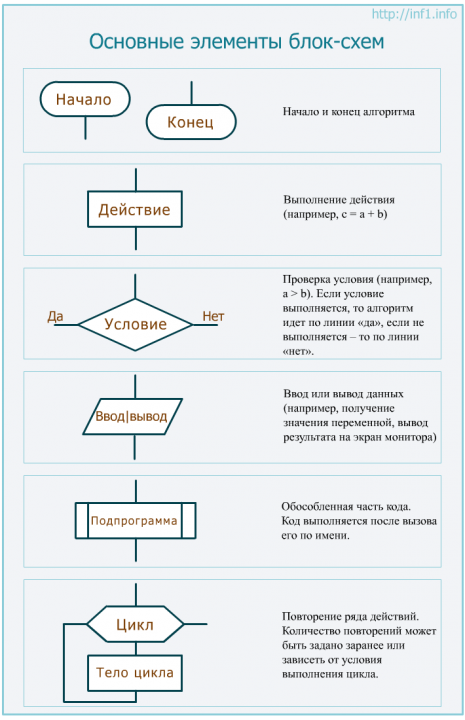  В условиях задачи на площадь прямоугольника:  3 способ. На алгоритмическом языке (псевдокоде). Запишем алгоритм задачи на школьном алгоритмическом языке: алг площадь (арг вещ a, b, рез вещ s) нач ввод а, b s:=a*b вывод "площадь прямоугольника со сторонами ", a, ", ", b, " равна ", s кон Алгоритмические структуры (типы алгоритмов) В рамках структурного программирования задачи, имеющие алгоритмическое решение, могут быть описаны с использованием следующих алгоритмических структур: Следование. Предполагает последовательное выполнение команд сверху вниз. Если алгоритм состоит только из структур следования, то он является линейным. Ветвление. Выполнение программы идет по одной из двух, нескольких или множества ветвей. Выбор ветви зависит от условия на входе ветвления и поступивших сюда данных. Цикл. Предполагает возможность многократного повторения определенных действий. Количество повторений зависит от условия цикла. Функция (подпрограмма). Команды, отделенные от основной программы, выполняются лишь в случае их вызова из основной программы (из любого ее места). Одна и та же функция может вызываться из основной программы сколь угодно раз. Описание различных алгоритмических структур на языке блок-схем
Формализации Черча, Тьюринга и Маркова В двадцатых годах XX века задача точного определения понятия алгоритма стала одной из центральных математических проблем. Она заключалась в попытке дать строгое математическое определение алгоритма, которое соответствовало бы имевшимся в то время интуитивным представлениям об алгоритме. Решение данной проблемы было получено в первой половине XX века. Рассмотрим следующие три варианта определения алгоритма: с точки зрения А. Черча и С. Клини, в алгоритмическом процессе вычисляется значение некоторой функции f(x1, x2,…, xn), определенной на множестве натуральных чисел. Строгое определение алгоритма, предложенное Черчем и Клини, основано на понятии частично рекурсивной функции. Они предложили отождествить интуитивное понятие «алгоритм» со строгим математическим понятием «частично рекурсивная функция»; с точки зрения английского математика А. Тьюринга алгоритмический процесс – это работа некоторой воображаемой вычислительной машины – машины Тьюринга. Он предложил отождествить интуитивное понятие «алгоритм» с точным понятием «машина Тьюринга». Также в качестве вычислительной машины рассматривается машина с неограни-ченными регистрами (МНР). Это абстрактная машина, более сходная с реальным компьютером по сравнению с машиной Тьюринга; Третий вариант определения алгоритма предложил в 1947 г. российский математик А. А. Марков. С его точки зрения, алгоритмический процесс – это переработка слов некоторого алфавита с помощью точно описанных правил переработки. Вместо интуитивного понятия «алгоритм» А.А.Марков вводит строгое понятие «нормальный алгорифм». Для теории сложности вычислений, выбор модели, в которой конструируются алгоритмы, не имеет принципиального значения. Существуют способы реализации одних алгоритмических моделей с помощью других. При этом сохраняется принадлежность алгоритмов определенному классу сложности. Алгоритм, записанный в виде программы на языке программирования высокого уровня, также может быть смоделирован с помощью одной из упомянутых формальных моделей. Итог Итак, в широко распространенных определениях алгоритма (в рамках школьного курса информатики) можно выделить следующие составляющие: Алгоритм – это … конечная последовательность указаний … … на языке понятном исполнителю, … … задающая процесс решения задач определенного типа … … и ведущая к получению результата, однозначно определяемого допустимыми исходными данными. В последнем пункте определения говорится о том, что результат выполнения алгоритма напрямую зависит от исходных данных. Т.е. один и тот же алгоритм при разных исходных данных даст разные результаты. С другой стороны, если одному и тому же алгоритму передать несколько раз одни и те же данные, он должен столько же раз выдать один и тот же результат. Изучение алгоритмов имеет большую практическую значимость. Это связано с тем, что создание алгоритма предполагает подробное описание каждого шага решения задачи, и в конечном итоге шаг алгоритма может быть достаточно прост для выполнения его компьютером. А значит, задачи, для которых можно выработать алгоритм их решения, могут быть автоматизированы, т.е. переложены «на плечи» машин. Однако следует всегда помнить, что не все задачи имеют алгоритмическое решение. При этом для тех задач, которые все-таки имеют алгоритмическое решение, могут быть разработаны различные алгоритмы. Но наиболее эффективным, скорее всего, будет только один. Контрольные вопросы: Кто был автором первых алгоритмов? Для чего применялись первые алгоритмы? Что понимается под алгоритмом сегодня? Дайте определение алгоритма. Опишите основные принципы построения и выполнения алгоритма. Каким образом может протекать алгоритмический процесс? Кто разрабатывает алгоритмы? Кто выполняет алгоритмы? Какие бывают алгоритмы в зависимости от их исполнителей? Что входит в систему команд исполнителя? Что входит в среду исполнителя? Какие языки называются алгоритмическими? Какие они бывают? Как называется алгоритм, записанный на языке программирования? На сегодняшний день существуют ли алгоритмы для всех классов задач? Какими основными свойствами должен обладать алгоритм? Раскройте смысл каждого требования. Каким образом можно записать алгоритм? Какими недостатками обладает каждый способ записи алгоритма? Приведите примеры записи алгоритмов. Какие основные обозначения используются в блок-схемах? Как соединяются различные блоки? Как читаются блок-схемы? Какие существуют основные алгоритмические конструкции? Что каждая из них описывает? Приведите описание базовых алгоритмических конструкций на языке блок-схем и Алгоритмическом языке. Когда было получено строгое математическое определение алгоритма? Дайте строгое определение алгоритма с точки зрения Черча и Клини, Тьюринга, Маркова. |










