Заказ №129893. Задача 1 Дано Рис. 1 Решение
 Скачать 1.17 Mb. Скачать 1.17 Mb.
|
|
Варианты № 1.2.3.4.5. 6 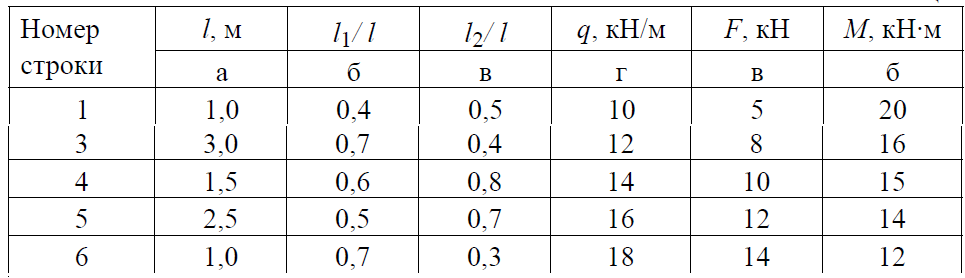 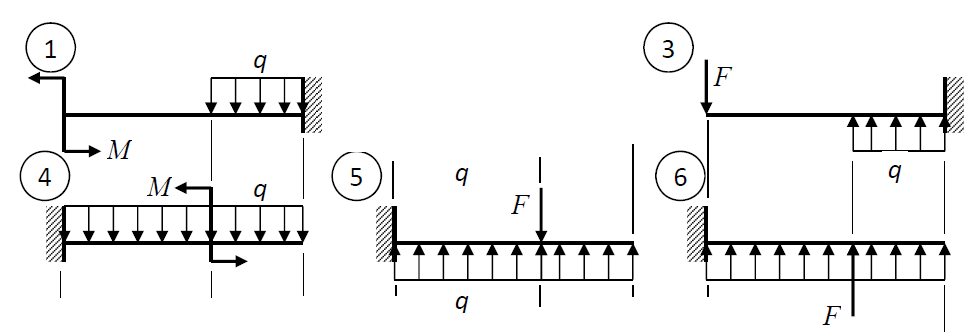 Задача 1 Дано:  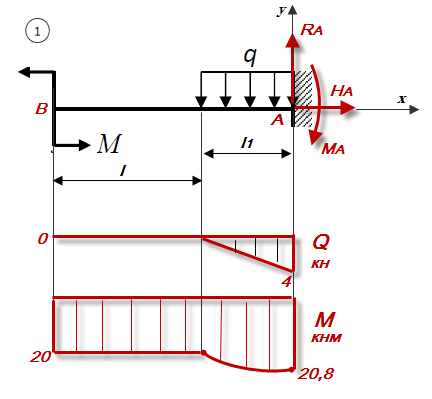 Рис.1 Решение 1. Определяем реакции опор. В защемлении возникают три реактивных усилия Для их определения составим уравнения равновесия: Составляем уравнения равновесия Проверим правильность определения реакций опор. Для этого составим уравнение равновесия – сумму моментов всех сил относительно любой точки балки, кроме точки А, например, точки В: 0=0 Реакции опор рассчитаны верно. В поперечных сечениях балки возникают изгибающие моменты При решении задачи используем известное правило знаков внутренних усилий: поперечная сила 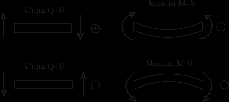 Рис. 2 Разобьём балку на 2 силовых участка. Границами участков являются сечения, в которых приложены сосредоточенные моменты и силы, а также начало и конец распределённой нагрузки. Используя метод сечений, найдём изгибающие моменты Первый участок (справа налево) Получаем 2 участок (справа налево) Получаем По найденным значениям строим эпюры Максимальное значение Максимальное значение Вариант 3  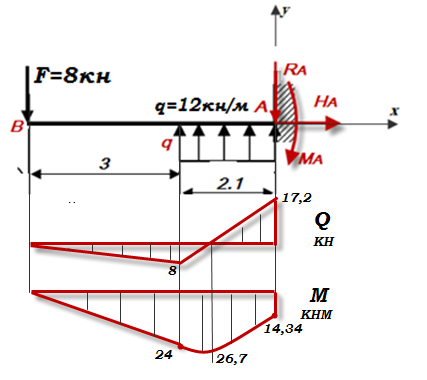 Дано : 1. Определяем реакции опор. В защемлении возникают три реактивных усилия Для их определения составим уравнения равновесия: Составляем уравнения равновесия Проверим правильность определения реакций опор. Для этого составим уравнение равновесия – сумму моментов всех сил относительно любой точки балки, кроме точки А, например, точки В 0=0 Реакции опор рассчитаны верно. В поперечных сечениях балки возникают изгибающие моменты При решении задачи используем известное правило знаков внутренних усилий: поперечная сила  Рис. 2 Разобьём балку на 2 силовых участка. Границами участков являются сечения, в которых приложены сосредоточенные моменты и силы, а также начало и конец распределённой нагрузки. Используя метод сечений, найдём изгибающие моменты Первый участок (слева направо) Получаем 2 участок (слева направо) Получаем На участке 2 есть максимум функции По найденным значениям строим эпюры Максимальное значение Максимальное значение 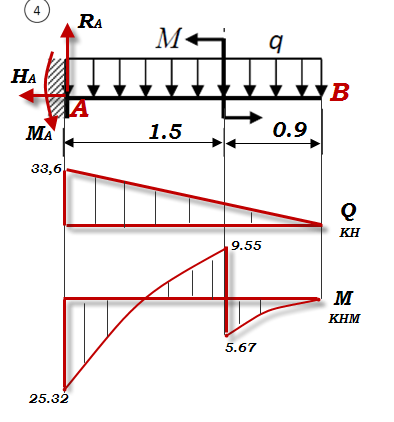  1. Определяем реакции опор. В защемлении возникают три реактивных усилия Для их определения составим уравнения равновесия: Составляем уравнения равновесия Проверим правильность определения реакций опор. Для этого составим уравнение равновесия – сумму моментов всех сил относительно любой точки балки, кроме точки А, например, точки В: 0=0 Реакции опор рассчитаны верно. В поперечных сечениях балки возникают изгибающие моменты При решении задачи используем известное правило знаков внутренних усилий: поперечная сила  Рис. 2 Разобьём балку на 2 силовых участка. Границами участков являются сечения, в которых приложены сосредоточенные моменты и силы, а также начало и конец распределённой нагрузки. Используя метод сечений, найдём изгибающие моменты Первый участок (справа налево) Получаем 2 участок (справа налево) Получаем По найденным значениям строим эпюры Максимальное значение Максимальное значение 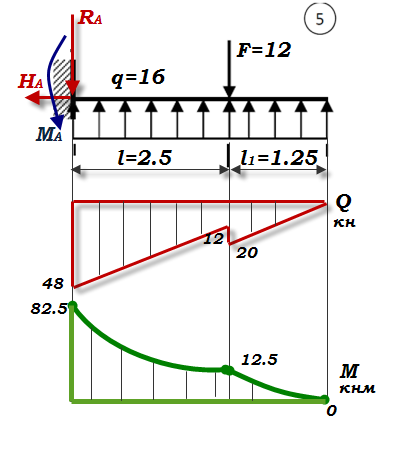  Дано : 1. Определяем реакции опор. В защемлении возникают три реактивных усилия Для их определения составим уравнения равновесия: Составляем уравнения равновесия Проверим правильность определения реакций опор. Для этого составим уравнение равновесия – сумму моментов всех сил относительно любой точки балки, кроме точки А, например, точки В 0=0 Реакции опор рассчитаны верно. В поперечных сечениях балки возникают изгибающие моменты При решении задачи используем известное правило знаков внутренних усилий: поперечная сила  Рис. 2 Разобьём балку на 2 силовых участка. Границами участков являются сечения, в которых приложены сосредоточенные моменты и силы, а также начало и конец распределённой нагрузки. Используя метод сечений, найдём изгибающие моменты Первый участок (справа налево) Получаем 2 участок (справа налево) Получаем По найденным значениям строим эпюры Максимальное значение Максимальное значение 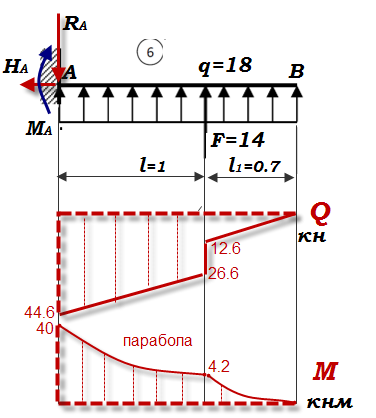 Рис. 1 Дано : 1. Определяем реакции опор. В защемлении возникают три реактивных усилия Для их определения составим уравнения равновесия: Составляем уравнения равновесия Проверим правильность определения реакций опор. Для этого составим уравнение равновесия – сумму моментов всех сил относительно любой точки балки, кроме точки А, например, точки В 0=0 Реакции опор рассчитаны верно. В поперечных сечениях балки возникают изгибающие моменты При решении задачи используем известное правило знаков внутренних усилий: поперечная сила  Рис. 2 Разобьём балку на 2 силовых участка. Границами участков являются сечения, в которых приложены сосредоточенные моменты и силы, а также начало и конец распределённой нагрузки. Используя метод сечений, найдём изгибающие моменты Первый участок (справа налево) Получаем 2 участок (справа налево) Получаем По найденным значениям строим эпюры Максимальное значение Максимальное значение 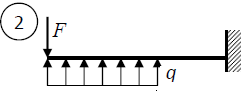  Дано : 1. Определяем реакции опор. В защемлении возникают три реактивных усилия 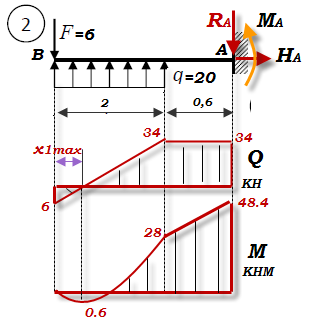 Рис.1 Для их определения составим уравнения равновесия: Составляем уравнения равновесия Проверим правильность определения реакций опор. Для этого составим уравнение равновесия – сумму моментов всех сил относительно любой точки балки, кроме точки А, например, точки В 0=0 Реакции опор рассчитаны верно. В поперечных сечениях балки возникают изгибающие моменты При решении задачи используем известное правило знаков внутренних усилий: поперечная сила 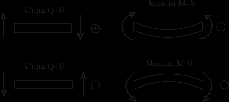 Рис. 2 Разобьём балку на 2 силовых участка. Границами участков являются сечения, в которых приложены сосредоточенные моменты и силы, а также начало и конец распределённой нагрузки. Используя метод сечений, найдём изгибающие моменты Первый участок (слева направо) Получаем 2 участок (слева направо) Получаем На участке 1 есть максимум функции По найденным значениям строим эпюры Максимальное значение Максимальное значение |
