Электростатика Кр №3 Вариант 3. Задачки. Задача 1 Определите в точке a с координатами x 3, y
 Скачать 327.5 Kb.
|
|
К/р №3 Вариант 3 Задача 1 Определите в точке A с координатами x3, y3 напряженность и потенциал электростатического поля, созданного двумя точечными зарядами q1 с координатами x1, y1 и q2 с координатами x2, y2; силу, действующую на заряд, а также работу по переносу заряда q3 в бесконечность. Заряды находятся в вакууме.
Определим расстояния между зарядами:   ,  ,  .Напряженность электрического поля точечного заряда:  .Согласно рисунку, имеем:  , , 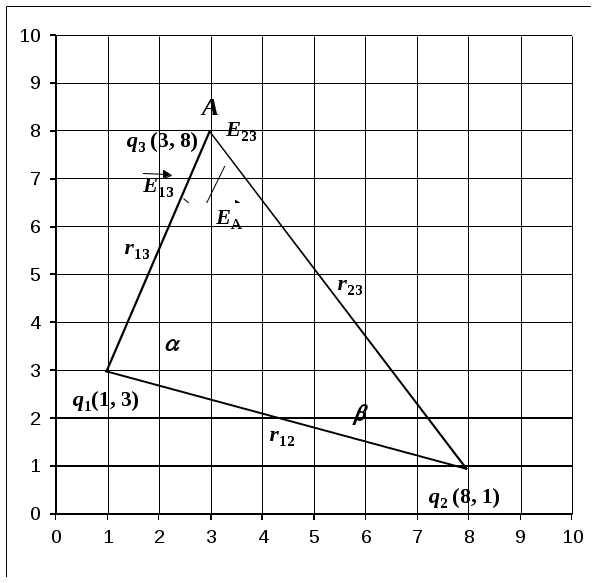где  ,  . Здесь  ,  , ,  .Тогда получаем: 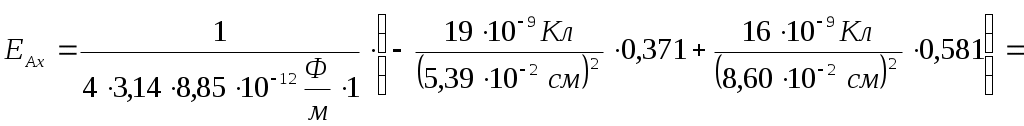  ,  , .Потенциал поля точечного заряда:  .В нашем случае: 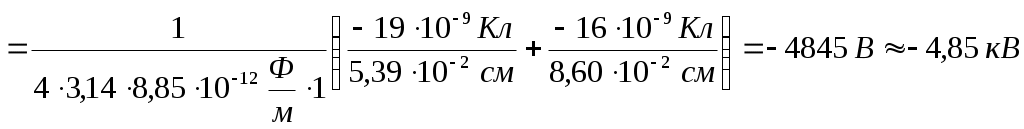  .Силу, действующую на заряд q3, определим из выражения:  .Следовательно,  .Работа, совершаемая электрическим полем при перемещении точечного заряда q3 из точки A в бесконечность будет равна:  .Вопросы для самоконтроля: 1) Сформулируйте закон сохранения электрических зарядов. В замкнутой системе при любых взаимодействиях тел алгебраическая сумма зарядов всех тел остается постоянной:  ,где  – алгебраическая сумма зарядов, входящих в изолированную систему, n – число зарядов.Этот экспериментально установленный факт называется законом сохранения электрического заряда. Нигде и никогда в природе не возникает и не исчезает заряд одного знака. Появление каждого положительного заряда всегда сопровождается появлением равного по абсолютному значению отрицательного заряда. Ни положительный, ни отрицательный заряд не могут исчезнуть в отдельности один от другого, они могут лишь взаимно нейтрализовать друг друга, если равны по абсолютному значению. 2) Как определить силу взаимодействия между двумя точечными зарядами? Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Силы электростатического взаимодействия зависят от формы и размеров взаимодействующих тел и характера распределения зарядов на них. Силы взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению абсолютных значений зарядов и обратно пропорциональна квадрату расстояния между ними:  .Если тела находятся в среде с диэлектрической проницаемостью , тогда сила взаимодействия будет ослабляться в раз:  .Силы взаимодействия двух точечных неподвижных тел направлены вдоль прямой, соединяющей эти тела. 3) Что является силовой характеристикой электростатического поля? В чем состоит принцип суперпозиции полей? Напряженность  – векторная, силовая характеристика электрического поля. Напряженность поля равна силе, действующей на единичный, пробный заряд, помещенный в данную точку поля:  .Напряженность электрического поля точечного заряда:  .Принцип суперпозиции (наложения) электрических полей: Напряжённость поля системы зарядов равна векторной сумме напряжённостей полей, которые создавал бы каждый из зарядов системы в отдельности:  .4) Что является энергетической характеристикой поля и как она связана с силовой характеристикой? Потенциал электрического поля – скалярная, энергетическая характеристика поля. Потенциал электрического поля равен энергии, которой обладает единичный пробный заряд в данной точке поля:  .Потенциал поля точечного заряда:  .Связь между напряженностью и потенциалом электрического поля выражается соотношением:  .6) Как определяется работа в электростатическом поле? Работа, совершаемая электрическим полем при перемещении точечного заряда q из одной точки поля, имеющей потенциал 1, в другую, имеющую потенциал 2: A12 = q(φ1 – φ2). Если заряд q из точки с потенциалом φ удаляется на бесконечность (где потенциал равен нулю), работа сил поля будет равна: A = qφ. |