Задачи. Задача 1 Решить задачу Коши для дифференциального уравнения 2(2) 21324х

• Название: Задача 1 Решить задачу Коши для дифференциального уравнения 2(2) 21324х
• Анкор: fdgfd
• Дата: 20.02.2023
• Размер: 443.13 Kb.
• Имя файла: Задачи.docx
• Тип: Задача; #947356

Задача 1

Решить задачу Коши для дифференциального уравнения:

2+(-2) *2+1*3=2-4х

y(0)=3,y'(0)=2



При постановке задачи Коши, указываются так называемые начальные условия, позволяющие однозначно выделить искомое частное решение из общего. Эти условия включают в себя значения функции и всех её производных до n-1 включительно (где -порядок дифференциального уравнения), заданные в одной и той же точке x0

Поясним вышесказанное на конкретном примере. Пусть нам требуется найти частное решение дифференциального уравнения: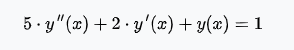



удовлетворяющее начальным условиям: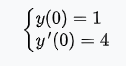



Первым делом, используя различные методы (Бернули, вариации произвольной постоянной Лагранжа), сначала находим общее решение данного дифференциального уравнения:



Теперь, для поиска частного решения, нам необходимо использовать заданные начальные условия. Для этого, находим производную функции y(x) полученной ранее: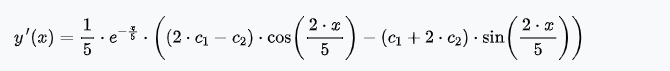



Далее, поставляем начальные условия в функцию у(х) и её производную у'(х)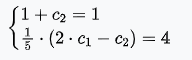



Задание 5.2

Найти общее решение дифференциального уравнения первого порядка

1. 
   2+1/x*y=1/x*sinx
   

w = 1 / ((w - y/x)/w)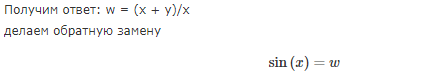



Ответ:



2. у  е  у  х

у=е^2х–5е^х–2
Найдем производную, равна она: 2е^2х–5е^х
Приравниваем к нулю:
2е^2х–5е^х=0
е^x(2e^х–5)=0
e^x=0 – не имеет корней
2x^x–5=0
2e^x=5
e^x=5/2
x=ln5/2
y(ln5/2)=e^2ln5/2–5e^ln5/2–2=25/4–25/2–2=6,25–12,5–2=–8,25
y(–2)=е^–4–5е^–2–2 > –8,25
y(1)=е²–5е¹–2 > –8,25
Ответ:–8,25

3.







4. 2*y = x^2 + x + 3





7.









8. 2*y²=e^-5x++2x+1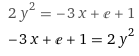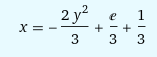









9. 2-1/x*y=x*cos(2x)





10. (x⁴+y³)dx+3xy² dy=0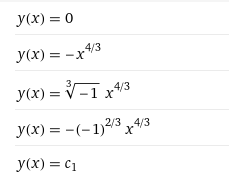



Задача 5.3

1.(2)²=у2²

4=4у

4у=4

4у/4=4/4

4/4=1

У=1

2. 
   2-1/х*2=хе^2х
   

2-2/х=е²х²

2(х-1)/х=е²х³

2x-2= е²х³

-e²x³+2x-2=0

-e²x³-2x+2=0

x³-2x/e²=0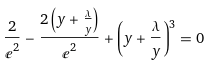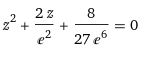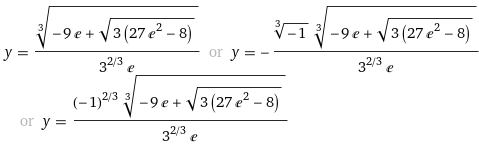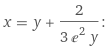

3. 
   2²-2*2ctgx=sin³*x
   

4. 
   2²xln=2
   

4x+3+4x=2604x+3+4x=260

Перенесем 260260 в левую часть уравнения, вычитая данный член из обеих частей.

4x+3+4x−260=04x+3+4x-260=0

Factor out 4x4x from the expression.

4x(64+1)4x(64+1)

Поскольку −260-260 не содержит искомой переменной, переместим его в правую часть уравнения, прибавив 260260 к обоим частям.

4x+3+4x=260=2604x+3+4x=260=260

Складываем 6464 и 11, получая 6565.

4x⋅65=2604x⋅65=260

Перенесем 6565 в левую часть выражения 4x⋅654x⋅65.

65⋅4x=26065⋅4x=260

Разделим каждый член на 6565 и упростим.

Нажмите, чтобы увидеть больше шагов...

4x=44x=4

Так как основания равны, два выражения равны только тогда, когда равны степени.

x=1x=1

Возьмем натуральный логарифм от обеих частей уравнения, чтобы из показателя степени убрать переменную.

ln(4x)=ln(4)ln(4x)=ln(4)

Воспользуемся правилами логарифмирования, чтобы вынести xxиз степени.

xln(4)=ln(4)xln(4)=ln(4)

Записываем ln(4)ln(4) как ln(22)ln(22).

xln(22)=ln(4)xln(22)=ln(4)

Разгалаем ln(22)ln(22) путем переноса 22за знак логарифма.

x(2ln(2))=ln(4)x(2ln(2))=ln(4)

Избавимся от скобок, заключающих 2ln(2)2ln(2).

x⋅(2ln(2))=ln(4)x⋅(2ln(2))=ln(4)

Перенесем 22 в левую часть выражения x⋅2x⋅2.

2⋅(xln(2))=ln(4)2⋅(xln(2))=ln(4)

Умножив 22 на xx, получим 2x2x.

2xln(2)=ln(4)2xln(2)=ln(4)

Упростим левую часть уравнения.

Нажмите, чтобы увидеть больше шагов...

x(2ln(2))=ln(4)x(2ln(2))=ln(4)

Решим относительно xx.

Нажмите, чтобы увидеть больше шагов...

x=ln(4)2ln(2)x=ln(4)2ln(2)

Проверим каждое решение первого множества решений, подставив в исходное уравнение 4x+3+4x=2604x+3+4x=260. В данном случае решения верны.

x=ln(4)2ln(2)x=ln(4)2ln(2)

x≈1
2.)...
(12)−6+x=2(12)-6+x=2

Применим правило произведения к 1212.

1−6+x2−6+x=21-6+x2-6+x=2

Единица в любой степени равна единице.

12−6+x=212-6+x=2

Перейдем в уравнении к эквивалентным выражениям, имеющим одинаковое основание.

26−x=226-x=2

Так как основания равны, два выражения равны только тогда, когда равны степени.

6−x=16-x=1

Решим относительно xx.

Нажмите, чтобы увидеть больше шагов...

x=5x=5

Проверим каждое решение первого множества решений, подставив в исходное уравнение (12)−6+x=2(12)-6+x=2. В данном случае решения верны.

x=5

3).....
(√2)x=116(2)x=116

Избавимся от скобок, заключающих √22.

√2x=1162x=116

Перейдем в уравнении к эквивалентным выражениям, имеющим одинаковое основание.

√2x=√2−82x=2-8

Так как основания равны, два выражения равны только тогда, когда равны степени.

x=−8x=-8

Проверим каждое решение первого множества решений, подставив в исходное уравнение (√2)x=116(2)x=116. В данном случае решения верны.

x=−8

5. 
   2²=2+x
   

4=2+x

X=4-2

X=2

6. 
   2⁴=x*sin*x
   

7. 
   2⁴=3*2²+5x-2
   

8. 
   4*2²=у
   

9. 
   2²=2+х
   

10. 
    2²=3*2-2у+х+3
    

Задача 5.4

2=cosx-y²*1=1

При постановке задачи Коши, указываются так называемые начальные условия, позволяющие однозначно выделить искомое частное решение из общего. Эти условия включают в себя значения функции и всех её производных до n-1  включительно (где -порядок дифференциального уравнения), заданные в одной и той же точке x0

Поясним вышесказанное на конкретном примере. Пусть нам требуется найти частное решение дифференциального уравнения: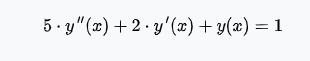



удовлетворяющее начальным условиям: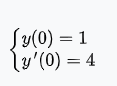



Первым делом, используя различные методы (Бернули, вариации произвольной постоянной Лагранжа), сначала находим общее решение данного дифференциального уравнения: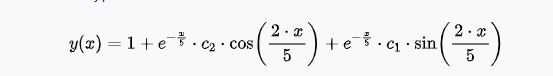



Теперь, для поиска частного решения, нам необходимо использовать заданные начальные условия. Для этого, находим производную функции  y(X)полученной ранее: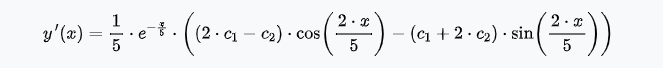



Далее, поставляем начальные условия в функцию y(x)  и её производную y (x)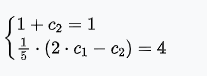



Решая полученную систему уравнений получаем значения произвольных c1 и с2 постоянных  и :



Подставляем полученные результаты в общее решение дифференциального уравнения, в результате получаем искомое частное решение: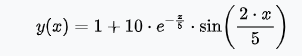



Задача 5.5

dx/at=0*x+1*y

dy/at=1*x+0*y

dtx/a=y(t)

dty/a=x(t)