Практическая работа физика. Практическая работа 1. Задача 1 Согласно теореме Гаусса, поток вектора напряжённости электрического поля e через замкнутую поверхность
 Скачать 45.97 Kb. Скачать 45.97 Kb.
|
|
Задача № 1 Согласно теореме Гаусса, поток вектора напряжённости электрического поля E через замкнутую поверхность S пропорционален суммарному электрическому заряду q, находящемуся внутри поверхности: 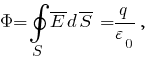 где ε0 = 8.8542·10-12 Ф/м - электрическая постоянная. Так как по формуле Остроградского-Гаусса поверхностный интеграл от любого векторного поля равен объёмному интегралу от его дивергенции: 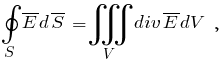 а заряд с переменной объёмной плотностью ρ также выражается с помощью объёмного интеграла: 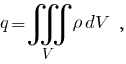 то теорему Гаусса можно записать в виде 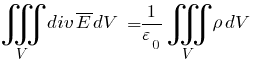 или 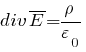 - дифференциальная формулировка теоремы Гаусса. Так как по определению 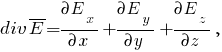 причём в данном случае напряжённость электрического поля изменяется только в направлении оси X, то есть проекции Ey, Ez постоянны и 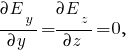 то 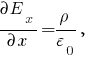 откуда 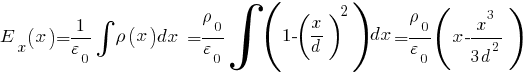 или, с учётом исходных данных (ρ = 1 нКл/м3 = 10-9 Кл/м3, d = 10 см = 0.1 м), 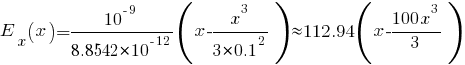 В/м. В/м.Задача № 2 Потенциал электростатического поля, создаваемого точечным зарядом q на расстоянии r от него, определяется выражением 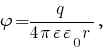 где ε - диэлектрическая проницаемость среды, ε0 = 8.8542·10-12 Ф/м - электрическая постоянная. Тогда потенциал поля бесконечно малого элемента отрезка с координатой x и зарядом dq будет равен 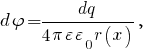 а полный потенциал поля всего отрезка составит (в соответствии с принципом суперпозиции) 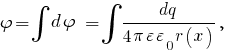 где интегрирование ведётся по всей длине отрезка. Для отрезка с линейной плотностью заряда λ имеем dq = λdx, а при отсчёте координаты x от середины отрезка расстояние до точки A равно r(x) = x + a, где -d < x < d, поэтому 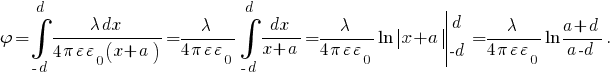 В данном случае λ = 12 нКл/м = 0.000000012 нКл/м, a = 5 см = 0.05 м, d = 1 см = 0.01 м, ε = 1 и 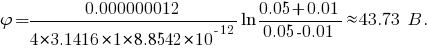 |
