3 задачи по физике Вариант2. 3 задачи по физике вар2. Задача 1 (
 Скачать 198.44 Kb.
|
|
Задача №1 (Вариант 12)  Найти индукцию магнитного поля в центре прямоугольного проводящего контура со сторонами a и b, по которому течет ток силой I. Дано: I=5 А, a=12 см=0,12 м b=6 см=0,06 м Найти: B=? Решение: Для решения задачи необходимо использовать:  Гн/м − магнитная постоянная.Рассмотрим четыре участка, АВ, ВС, СД, ДА. Направление вектора магнитной индукции на каждом участке определим по правилу буравчика. В точке О результирующий вектор магнитной индукции направлен от нас. Применим принцип суперпозиции.  (1)или в проекции на ось вектора   (2)Определим модуль вектора магнитной индукции на участке АВ. Индукция магнитного поля в произвольной точке О, созданного отрезком проводника с током конечной длины, определим используя закон Био - Савара - Лапласа. dB=μ0⋅I4⋅π⋅R⋅sinαdα, B=μ0⋅I4⋅π⋅R⋅∫α1α2sinαdα,B=μ0⋅I4⋅π⋅R⋅(cosα1−cosα2) (3). Где: R - расстояние от т. О до проводника; – α1 и α2 углы, образованные радиус-вектором, проведенном в т. О соответственно из начала и конца проводника, с направлением тока. Определим модуль вектора магнитной индукции на каждом участке. α2 = 3∙π/4, α1 = π/ 4. B=μ0⋅I4⋅π⋅R⋅(cosπ4−cos3⋅π4) , B=μ0⋅I4⋅π⋅R⋅(2–√2+2–√2) ,BBC=BDA=BCD=BAB=2–√⋅μ0⋅I4⋅π⋅R (5),R=d2 (6),B=4⋅2–√⋅μ0⋅I2⋅π⋅d, B=2⋅2–√⋅μ0⋅Iπ⋅d (7).B=2⋅2–√⋅4⋅π⋅10−7⋅5π⋅0,15=37,6⋅10−6. Ответ 9,43 мкТ получается если бы квадрат был изготовлен из проволоки длиной 15 см. Ответ: В = 37,6∙10-6 Тл. Согласно теореме Гаусса, поток вектора напряжённости электрического поля E через замкнутую поверхность S пропорционален суммарному электрическому заряду q, находящемуся внутри поверхности:  , (1)где  Ф/м - электрическая постоянная.Так как по формуле Остроградского-Гаусса поверхностный интеграл от любого векторного поля равен объёмному интегралу от его дивергенции:  (2)а заряд q с переменной объёмной плотностью ρ также выражается с помощью объёмного интеграла:  , (3)то теорему Гаусса можно записать в виде  (4)или  (5)- дифференциальная формулировка теоремы Гаусса. Так как по определению  (6)причём в данном случае напряжённость электрического поля изменяется только в направлении оси X, то есть проекции Ey, Ez постоянны и равны 0  то  (7)откуда  (8)В итоге подставив в формулу (8) все известные значения кроме x в, получаем  В/м. Ответ:  В/м.Задача №2 (Вариант 12) 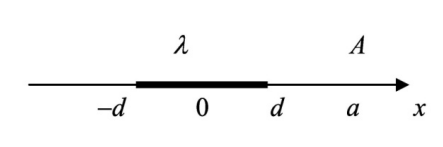 Найти потенциал электростатического поля, создаваемого отрезком прямой длиной 2d в точке A. Отрезок равномерно заряжен с линейной плотностью заряда . Точка A лежит на оси X, направленной вдоль отрезка, на расстоянии a от его середины. Дано:__a=8_см=0,08_мd=2_см=0,02_мНайти:_=Решение'>Дано:  a=8 см=0,08 м d=2 см=0,02 м Найти: =? Решение: В общем случае потенциал электростатического поля точечного заряда q на расстоянии r от него определяется формулой  , (1)где Ф/м - электрическая постоянная.Дифференцируя, для бесконечно малого заряда dq имеем  (2)В частности, для равномерно заряженного отрезка прямой l с линейной плотностью заряда λ имеем dq = λdl, откуда  (3)Для отрезка длиной 2d и точки A, расположенной на оси отрезка на расстоянии a>d от его середины расстояние r будет меняться в диапазоне от a-d до a+d, и потенциал в точке A будет равен   (4)В итоге подставляя в формулу (4) получаем  ВОтвет: =91,9 В Задача №3 (Вариант 12)  В схеме, приведенной на рисунке, ЭДС источников E1=2 В, E2=3 В, сопротивления резисторов R1=0,2 Ом, R2=1 Ом, R3=0,5 Ом, сопротивление амперметра равно RA. Найти показание амперметра. Внутренним сопротивлением источников пренебречь. Дано: E1=2 В E2=3 В R1=0,2 Ом R2=1 Ом R3=0,5 Ом RА=0,25 Ом Найти: I3=? Решение:  Запишем второе правило Кирхгофа для контура 1:  (1)Запишем второе правило Кирхгофа для контура 2:  (2)Запишем первое правило Кирхгофа для узла 0:  (3)Подставив формулу (3) в формулы (1) и (2), получим следующую систему из 2-х уравнений  (4)  Отсюда  (5) (6)В итоге подставляя в формулу (6) получаем  АОтвет: Амперметра показывает 2,91 А. |