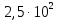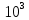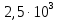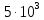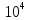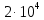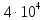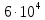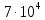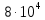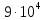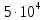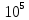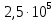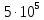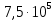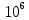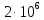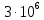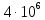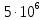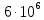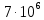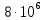ДКР электро Вариант 8.cleaned. Задача 1 задача 2 задача 3 задача 4 задача 5 8 5,24
 Скачать 197.74 Kb. Скачать 197.74 Kb.
|
|
Варианты заданий домашней контрольной работы
Вопросы 1 уровня Вопрос 5. Последовательное соединение проводников. При таком соединении проводники соединены последовательно друг за другом, то есть конец одного проводника соединяется с началом другого. Все проводники принадлежат одному проводу, на котором нет разветвлений. Это приводит к тому, что через любой из проводников протекает один и тот же ток, а общее напряжение на них будет складываться из напряжений на каждом.  последовательно соединенных проводников всегда можно заменить одним эквивалентным проводником. Сила тока Iэкв через этот проводник, напряжение Uэкв на нем, а также его сопротивление Rэкв будут определяться по правилам, отображенным в таблице.  Вопрос 24. Напряжение (U). Электрическое напряжение-это разность электрических потенциалов между двумя точками, которая (в статическом электрическом поле) определяется как работа, необходимая на единицу заряда для перемещения испытательного заряда между двумя точками. Вопросы 2 уровня Вопрос 8. Основные параметры переменного тока. Мгновенное и максимальное значения ЭДС и величина тока. Переменный ток — электрический ток, направление и сила которого изменяются периодически. Так как обычно сила переменного тока изменяется по синусоидальному закону, то переменный ток представляет собой синусоидальные колебания напряжения и силы тока. Поэтому к переменному току применимо все то, что относится к синусоидальным электрическим колебаниям. Синусоидальные колебания — колебания, при которых колеблющаяся величина изменяется по закону синуса. В данной статье поговорим о параметрах переменного тока. Изменение ЭДС и изменение тока линейной нагрузки, подключенной к такому источнику, будет происходить по синусоидальному закону. При этом переменные ЭДС, переменные напряжения и токи, можно характеризовать основными четырьмя их параметрами: период; частота; амплитуда; действующее значение. Есть и вспомогательные параметры: угловая частота; фаза; мгновенное значение. Величину переменной электродвижущей силы, силы тока, напряжения и мощности в любой момент времени называют мгновенными значениями этих величин и обозначают соответственно строчными буквами (e, i, u, p). Вопрос 37. Напряженность магнитного поля. Вокруг проводника или катушки с электрическим током всегда возникает магнитное поле. Магнитное поле постоянного магнита вызывается движением электронов по их орбитам в атоме. Магнитное поле характеризуется напряженностью. Напряженность 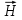 магнитного поля аналогична механической силе. Она является векторной величиной, т. е. имеет величину и направление. магнитного поля аналогична механической силе. Она является векторной величиной, т. е. имеет величину и направление.Магнитное поле, т. е. пространство вокруг магнита, можно представить заполненным магнитными линиями, которые принято считать выходящими из северного полюса магнита и входящими в южный (рис. 1). Касательные к магнитной линии показывают направление напряженности магнитного поля. Напряженность магнитного поля больше там, где магнитные линии гуще (на полюсах магнита или внутри катушки с током). Магнитное поле около проводника (или внутри катушки) тем больше, чем больше ток 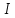 и число витков ω катушки. и число витков ω катушки.Напряженность магнитного поля H в любой точке пространства тем больше, чем больше произведение I∙ω и чем меньше длина магнитной линии: 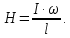 Из уравнения следует, что единицей измерения напряженности магнитного поля является ампер на метр (А/м). Для каждой магнитной линии в данном однородном поле произведения 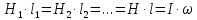 равны (рис. 1). равны (рис. 1).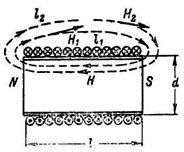 Рисунок 3 – Магнитное поле. Произведение 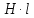 в магнитных цепях аналогично напряжению в электрических цепях и называется магнитным напряжением, а взятое по всей длине линии магнитной индукции называется намагничивающей силой (н. с.) Fм: в магнитных цепях аналогично напряжению в электрических цепях и называется магнитным напряжением, а взятое по всей длине линии магнитной индукции называется намагничивающей силой (н. с.) Fм: 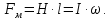 Намагничивающая сила Fм измеряется в амперах, но в технической практике вместо названия ампер применяется название ампер-виток, чем подчеркивается то, что Fм пропорциональна току и числу витков. ПРАКТИЧЕСКАЯ ЧАСТЬ Задача №1 Условие задачи: Согласно варианту, выбираем данные из таблицы 2. Найти величину токов через все резисторы (рис.20). 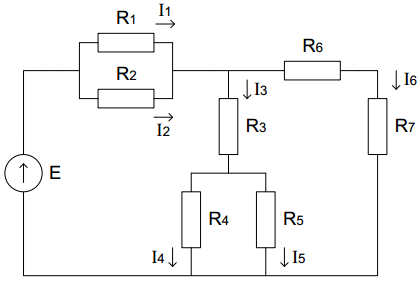 Рисунок 2 – Расчетная схема к задаче 1 Таблица 2 – Данные к задаче 1
Найдем полное сопротивление цепи: Резисторы 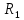 и и 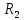 соединены параллельно. Тогда их общее сопротивление равно: соединены параллельно. Тогда их общее сопротивление равно: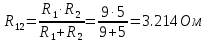 Резисторы 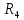 и и 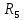 соединены параллельно. Тогда их общее сопротивление равно: соединены параллельно. Тогда их общее сопротивление равно: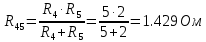 Схема примет вид: 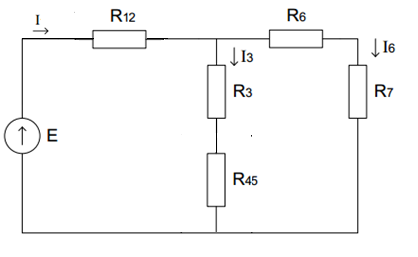 Рисунок 4 – Cхема после преобразования Резисторы 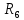 и и 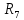 соединены последовательно. Тогда их общее сопротивление равно: соединены последовательно. Тогда их общее сопротивление равно: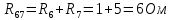 Резисторы 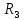 и и 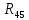 соединены последовательно. Тогда их общее сопротивление равно: соединены последовательно. Тогда их общее сопротивление равно: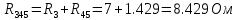 Схема примет вид: 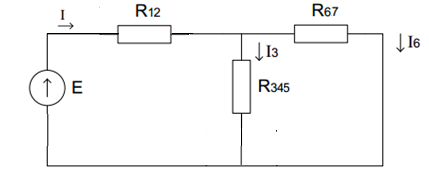 Рисунок 5 – Cхема после преобразования Резисторы 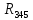 и и 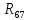 соединены параллельно. Тогда их общее сопротивление равно: соединены параллельно. Тогда их общее сопротивление равно: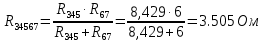 Резисторы 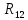 и и 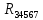 соединены последовательно. Тогда общее сопротивление цепи равно: соединены последовательно. Тогда общее сопротивление цепи равно: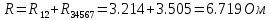 Сила тока в цепи по закону Ома равна 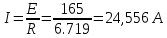 Напряжение на общем сопротивлении 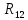 по закону Ома равно: по закону Ома равно: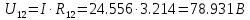 Так как из рисунка 3 два сопротивления 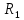 и и 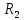 соединены параллельно, напряжение на каждом из них равно общему напряжению: соединены параллельно, напряжение на каждом из них равно общему напряжению: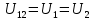 Определим напряжение на общем сопротивлении 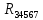 по второму закону Кирхгофа: по второму закону Кирхгофа: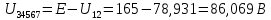 Так как из рисунка 5 два два сопротивления 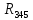 и и 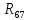 соединены параллельно, напряжение на каждом из них равно общему напряжению: соединены параллельно, напряжение на каждом из них равно общему напряжению: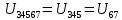 Тогда определим токи по закону Ома: 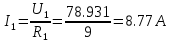 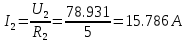 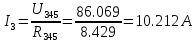 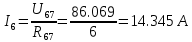 Напряжение на общем сопротивлении 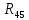 по закону Ома равно: по закону Ома равно: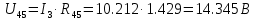 Так как из рисунка 3 два сопротивления 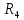 и и 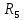 соединены параллельно, напряжение на каждом из них равно общему напряжению: соединены параллельно, напряжение на каждом из них равно общему напряжению: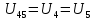 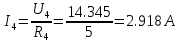 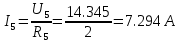 Задача №2   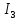 1 Условие задачи: Согласно варианту, выбираем данные из таблицы 3. Найти Е1, Е2, R2 (рис.21).         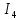 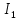 2 4 3 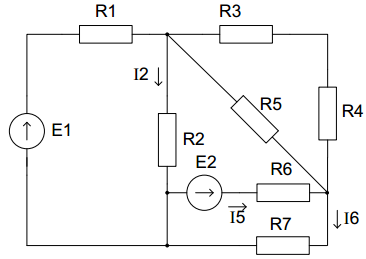 Рисунок 6 – Расчетная схема к задаче 2 Таблица 3 – Данные к задаче 2
Совместим узлы 2 и 4, тогда ток 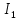 по первому закону Кирхгофа для узла 2: по первому закону Кирхгофа для узла 2: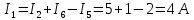 Для контура 234, выберем направление по часовой стрелке. Согласно второму закону Кирхгофа: 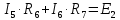 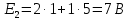 Преобразуем схему заменив участок 13 эквивалентным сопротивлением R345 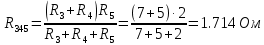 Схема примет вид: 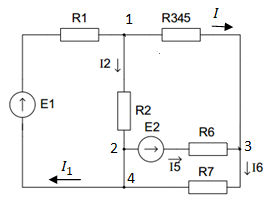 Рисунок 7 – Схема после преобразования Ток 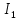 по первому закону Кирхгофа для узла 2: по первому закону Кирхгофа для узла 2: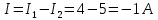 Для контура 123, выберем направление по часовой стрелке. Согласно второму закону Кирхгофа: 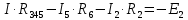 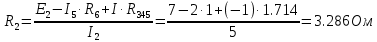 Для контура 124, выберем направление по часовой стрелке. Согласно второму закону Кирхгофа: 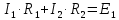 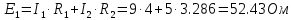 Задача №3 Условие задачи: Согласно варианту, выбираем данные из таблицы 4. Найти условия оптимального согласования нагрузки с резонансным контуром. Найти мощность, выделяемую в нагрузке Rн (рис. 22). 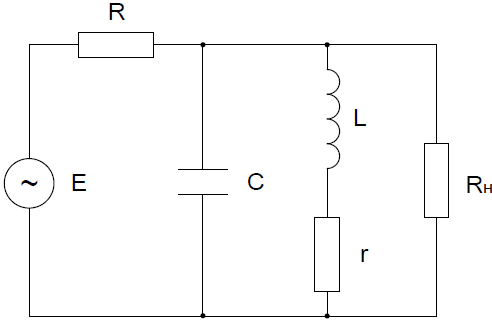 Рисунок 8 – Расчетная схема к задаче 3 Таблица 4 – Данные к задаче 3
Условием оптимального согласования нагрузки с резонансным контуром будет являться равенство 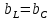 . При этом реактивное сопротивление цепи равно нулю, а резонансная частота равна: . При этом реактивное сопротивление цепи равно нулю, а резонансная частота равна: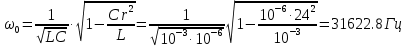 Определим сопротивления реактивных элементов в этом случае: 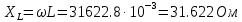 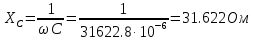 Задача №4 Условие задачи: В цепи (рис. 23) известно U, R1, R2, R3 ,R4, R5 (табл. 5). Определить токи в ветвях при разомкнутом и замкнутом ключе К. 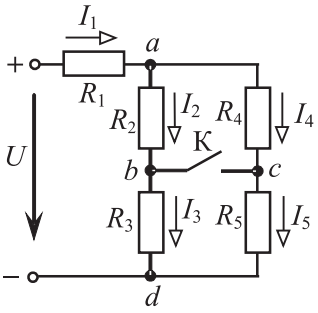 Рисунок 9 – Расчетная схема к задаче 4 Таблица 5– Данные к задаче 4
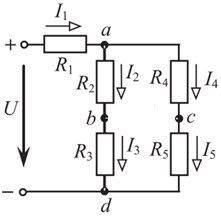 Рисунок 10 – Расчетная схема при разомкнутом ключе Найдем полное сопротивление цепи: Резисторы 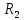 и и 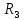 соединены последовательно. Тогда их общее сопротивление равно: соединены последовательно. Тогда их общее сопротивление равно: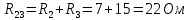 Резисторы 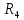 и и 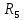 соединены последовательно. Тогда их общее сопротивление равно: соединены последовательно. Тогда их общее сопротивление равно: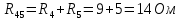 Резисторы 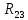 и и 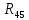 соединены параллельно. Тогда их общее сопротивление равно: соединены параллельно. Тогда их общее сопротивление равно: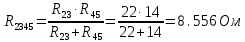 Резисторы 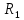 и и 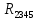 соединены последовательно. Тогда их общее сопротивление равно: соединены последовательно. Тогда их общее сопротивление равно: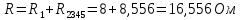 Сила тока в цепи по закону Ома равна 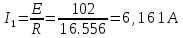 Напряжение на общем сопротивлении 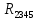 по закону Ома равно: по закону Ома равно: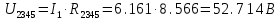 Так как из рисунка 10 два сопротивления 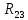 и и 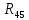 соединены параллельно, напряжение на каждом из них равно общему напряжению: соединены параллельно, напряжение на каждом из них равно общему напряжению: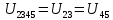 Тогда определим токи по закону Ома: 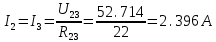 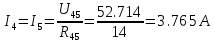 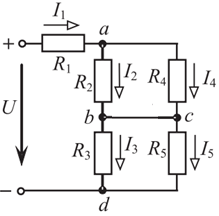 Рисунок 10 – Расчетная схема при замкнутом ключе Найдем полное сопротивление цепи: Резисторы 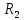 и и 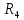 соединены параллельно. Тогда их общее сопротивление равно: соединены параллельно. Тогда их общее сопротивление равно: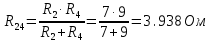 Резисторы 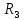 и и 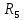 соединены параллельно. Тогда их общее сопротивление равно: соединены параллельно. Тогда их общее сопротивление равно: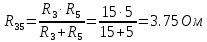 Резисторы 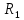 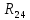 и и 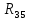 соединены последовательно. Тогда их общее сопротивление равно: соединены последовательно. Тогда их общее сопротивление равно: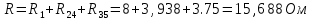 Сила тока в цепи по закону Ома равна 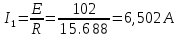 Напряжение на общем сопротивлении 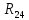 по закону Ома равно: по закону Ома равно: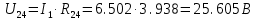 Напряжение на общем сопротивлении 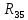 по закону Ома равно: по закону Ома равно: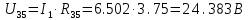 Тогда определим токи по закону Ома: 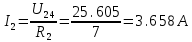 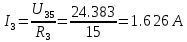 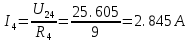 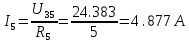 Задача № 5 Условие задачи: Рассчитать коэффициент передачи LR-четырехполюсника на частоте f = 100 Гц. Построить АЧХ и ФЧХ, если известно R и L. 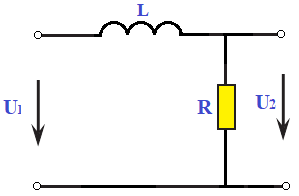 Рисунок 24 – Электрическая схема к задаче 5 Таблица 6 – Данные к задаче 5
1. Коэффициент передачи четырехполюсника 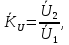 где 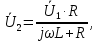 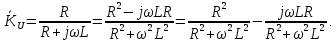 2. Для построения АЧХ и ФЧХ определим модуль и фазу комплексного коэффициента передачи 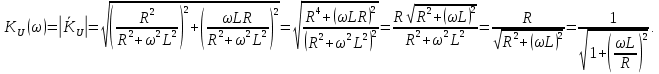 Обозначим 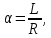 тогда тогда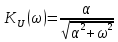 Вычислим 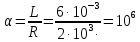 с-1 = 106 с-1. с-1 = 106 с-1.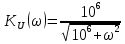 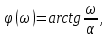 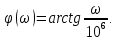 3. Для ряда значений циклической частоты ω рассчитаем KU(ω) и φ(ω). Результаты вычислений сведем в таблицу 1. По данным таблицы построим АЧХ (рис. 16) и ФЧХ (рис.17). Таблица 7 – Результаты вычислений KU(ω)
Таблица 8 – Результаты вычислений φ(ω)
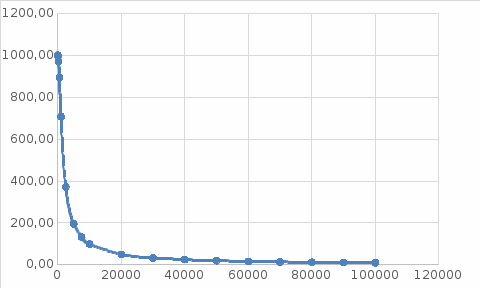 Рисунок 16 – АЧХ цепи 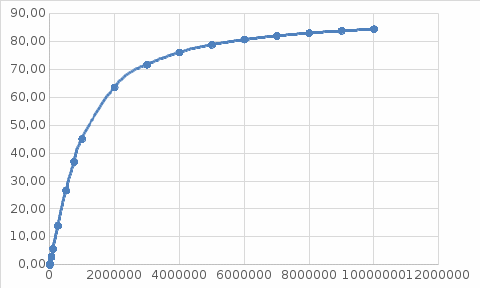 Рисунок 17 – ФЧХ цепи 4. Рассчитаем модуль и фазу коэффициента передачи на частоте f=100 Гц (ω=628 с-1). KU(ω) = 846,85, φ (ω) = 0,04°. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||