Задача двух тел. 8 Задача двух тел. Задача двух тел Уравнение движения в задаче двух тел

• Название: Задача двух тел Уравнение движения в задаче двух тел
• Анкор: Задача двух тел
• Дата: 23.11.2022
• Размер: 65.8 Kb.
• Имя файла: 8 Задача двух тел.docx
• Тип: Задача; #807242

Лекция 8

Задача двух тел

1. 
   Уравнение движения в задаче двух тел.
   

Задача двух тел – задача о движении двух материальных тел под действием взаимного тяготения. Никакие другие силы не учитываются, тела считаются точечными. Решая задачу двух тел в динамике Ньютона, можно получить законы Кеплера.

Рассмотрим движение двух тел, M -1-е тело и m – 2-е тело, под действием взаимного тяготения. Введем декартову систему координат, XYZ – инерциальную.

Пусть тел М и m в системе координат xyz.

Тогда

На тела М и m действуют равные по модулю, но взаимно противоположно направленные силы:







z

m

r₂ r

r₁

y

x

Каждое из этих тел будет двигаться под действием силы в соответствии со 2-м законом Ньютона.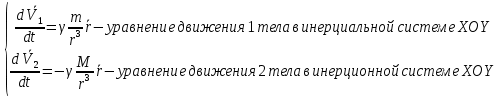





Перейдем в неинерциальную систему отсчета, привязанную к первому телу, для этого вычтем из 1-го уравнения второе



Обозначим: – скорость движения 2-го тела относительно первого,

∑M = m + M, получим



уравнение движения 2-го тела, m, в неинерциальной системе координат, привязанной к центру масс тела М.

Заметим, что законы Кеплера имеют место только в неинерциальной системе отсчета, когда начало координат привязано к центру масс одного из гравитирующих тел.

2. 
   Вывод 2-го закона Кеплера
   

Выведем 2-й закон Кеплера из рассмотрения задачи 2-х тел в рамках механики Ньютона. Обозначим



момент скорости – это

– модуль момента скорости в общем случае.

перпендикулярна плоскости, в которой находятся .

Если совпадают, или противоположны, по направлению, т.е.



.

В общем случае движения тел под действием силы тяжести может быть



Рассмотрим производную по времени от момента скорости









Следовательно, – в случае движения под действием силы тяжести момент скорости есть постоянный вектор. Он определяет постоянную ориентацию плоскости орбиты, в которой находятся векторы скорости и радиус-вектор 2-го тела.

Перепишем: = const(t).

где S = - площадь треугольника, построенного на векторах .

Следовательно, момент скорости равен удвоенной площади треугольника, образованного векторами и эта площадь неизменна при движении по орбите.

В задаче 2-х тел тело движется по орбите вокруг другого тела так, что радиус вектор остается в одной плоскости и за равные промежутки времени заметает равные площади –уточненный второй закон Кеплера.

Найдем угловую скорость движения тела по относительной орбите. Для этого введем полярную систему координат с центром в центре тела М, с координатами r и φ, где φ – угол между осью ОХ и вектором r. Это неинерциальная система отсчета. Запишем площадь треугольника, построенного на векторах в этой системе координат

S = dφ/dt

или

- угловая скорость движения тела по орбите.

3. 
   Вывод первого закона Кеплера.
   

Из уточненного второго закона Кеплера следует, что в задаче 2-х тел все движение происходит в одной плоскости, это позволяет упростить задачу, перейдя к двумерному рассмотрению. Введем двумерную декартову систему координат, XOY, с центром в центре тела М, плоскость XOY пусть совпадает с плоскостью орбиты тела m. Уравнение движения тела m в полярной системе координат запишем в проекциях на оси OX и OY:







аналогично, выразим вектор ускорения через его проекции на сои координат.

Заметим, что



Разделим каждое из уравнений на уравнение





Проинтегрируем эти уравнения:



А и В - const интегрирования

Выберем ось ОХ так, чтобы при , то есть скорость перпендикулярна оси ОХ, тогда А=0.

Найдем выражения для V_x и V_y



Подставим V_x и V_y в уравнения движения



Умножим 1-е уравнение на –sinφ, а второе уравнение умножим на cosφ и сложим уравнения, получим









Переобозначим:

или







Еще раз переобозначим:

-

Получили r =

– общее уравнение конических сечений в полярных координатах с центром в фокусе кривой. Здесь е – эксцентриситет кривой 2-го порядка, К – параметр, определяемый физическими характеристиками гравитирующих тел,



Итак, в общем случае получили, что под действием силы гравитации тело m в неинерциальной системе отсчета с центром в центре масс тела М движется по орбите, которая описывается уравнением конических сечений– это уточненный 1 закон Кеплера.

В зависимости от значения е возможны частные случаи:

1. 
   е = 0, r = K = const – тело движется по окружности.
   
2. 
   0 < e < 1, так как ,то r везде конечное число, то есть кривая замкнута – это эллипс. Из свойств функции cosφ следует, что эллипс симметричен относительно прямой ОХ.
   
3. 
   е = 1, r = , при
   
4. 
   е > 1, r = , при cos - орбита –гипербола.
   

cosφ

1

0

-1 2 φ



П r φ

F₁ O F₂ A

4. 
   Вывод 3 закона Кеплера.
   

Рассмотрим свойства эллипса, которые следуют из уравнения конических сечений в полярных координатах:

1. 
   Симметричен относительно прямой, соответствующей направлению
   
2. 
   Симметричен относительно прямой, перпендикулярной большой оси и проходящей через точку О, то есть у эллипса два фокуса, F₁ и F₂.
   
3. 
   При , cos = 1, r = Q = тело с массой m в апоцентре, то есть на максимальном расстояние от F₁.
   

При - тело m в перицентре, то есть на минимальном расстоянии от фокуса F₁.

Так как Q = А(1 + e), q = А(1 - e)



Поскольку

большая полуось орбиты определяется физическими характеристиками взаимодействующих тел. Использовали для большой полуоси большую букву А, так как законы Кеплера выведены для относительной орбиты.

Из уравнения конических сечений для эллипса можно вывести уравнение для скорости движения 2-го тела по орбите вокруг первого тела:

А =



или v =

Как и все законы Кеплера, это уравнение для скорости имеет место в неинерциальной системе отсчета.

Воспользуемся уравнением для площади эллипса

S = πАВ

Так как В = А

То

Скорость изменения площади, заметаемой радиус-вектором – это половина момента скорости.



Проинтегрировав по всему периоду, получим



Так как I = const, отсюда

Но мы переобозначили:





–

уточненный 3-й закон Кеплера

5. 
   Типы орбит в задаче 2-х тел
   

Интегрируя уравнения движения каждого из тел в инерциальной системе отсчета в задаче 2-х тел, получим закон сохранения энергии: полная энергия каждого из тел сохраняется:





E = E₁ + E₂ = const

Обратим внимание, что гравитационная потенциальная энергия каждого их тел, находящихся в поле тяготения, одинакова:

П₁ = П₂ = -γmМ/r.

Тип орбиты тела m и его скорость определяются его полной энергией, Е.

–

уравнение для скорости движения тела m по орбите в инерциальной системе отсчета.

Рассмотрим 3 случая:

1. 
   Е > 0 - полная энергия положительна, когда кинетическая энергия тела больше его гравитационной потенциальной энергии.
   

При r V – при удалении от гравитирующего тела скорость стремится к постоянной конечной величине, т.е. движение стремится к прямолинейному. Форма орбиты - гипербола, асимптоты которой приближаются к двум прямым.

2. 
   Е = 0, ∞, V 0
   

При удалении от гравитирующего тела скорость стремится к нулю форма орбиты – парабола. Скорость максимальна, когда rминимально, r = q,

- параболическая скорость.

Скорость, при которой орбита становится незамкнутой, называется параболической скоростью, при этом q - расстояние в перигелии.

3. 
   Е < 0 – полная энергия отрицательная, когда кинетическая энергия тела меньше по модулю его гравитационной энергии.
   

для любого значения r, в том числе



Орбита замкнута, в .

,

скорость движения по эллипсу переменная, чем больше r, тем меньше V.

4. 
   Частный случай замкнутой орбиты - круговая орбита.
   

При этом скорость движения постоянная и определяется равенством двух постоянных по модулю сил: силы тяжести и центробежной силы.



– скорость движения по круговой орбите в инерциальной системе отсчета.

Уравнение для скорости движения по круговой орбите можно получить и из уравнения конических сечений. Подставив туда е = 0, получим




отсюда – скорость движения тела по круговой орбите в неинерциальной системе отсчета, привязанной к центру масс второго тела.

В этом случае r = q = a = Q

Заметим, что

Итак:

V = V_c – движение по кругу

V_c < V < – движение по эллипсу.

V > V_с √2 – движение по параболе или гиперболе.
Подчеркнем, что в случае Солнечной системы отличие инерциальной системы отсчета, привязанной к центру масс, от неинерциальной системы, привязанной к центру Солнца, практически незаметно, так как масса Солнца намного больше массы любой из планет.