Контрольная работа по дисциплине «Планирование эксперимента в системах автоматизации технологических процессов и производств» Ва. Планирование. Задача Имеются данные о пробеге автомобилей на 10. 01. 2012 г. Целью обработки статистической информации является построение полигона и гистограммы распределения,
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Контрольная работапо дисциплине «Планирование эксперимента в системах автоматизации технологических процессов и производств» Вариант 3 Выполнил: студент Проверил:Санкт-Петербург-2022 Задача 1. Имеются данные о пробеге автомобилей на 10.01.2012 г. Целью обработки статистической информации является: построение полигона и гистограммы распределения, определение числовых характеристик выборки, построение интервальных оценок математического ожидания и дисперсии. Данные для анализа представлены в таблице 1.1. (пробег автомобилей указан в тыс. км.). Таблица 1.1
РешениеПроведем группировку исходных данных. Объём наблюдений: n=35. Количество интервалов определим по формуле Стерджесса: 𝑘 = 1 + 3.322 lg(𝑛) = 1 + 3.322 lg(35) = 6.129 ≈ 6. Наименьший элемент: 𝑥𝑚𝑖𝑛 = 6,6. Наибольший элемент: 𝑥𝑚𝑎𝑥 = 199,3. Размах R=𝑥𝑚𝑎𝑥 − 𝑥𝑚𝑖𝑛 = 199,3 − 6,6 = 192,7 Ширина одного интервала: 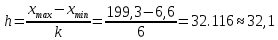 Для каждого интервала определим частоты ni, относительные частоты 𝑝∗ = 𝑛𝑖 𝑖 𝑛 и середины интервалов 𝑥∗ = 𝑥𝑖−1+𝑥𝑖, i=1,2,…,6. 𝑖 2
Построим гистограмму распределения:  Рисунок 1 – Гистограмма распределения Построим полигон распределения:  Рисунок 2 – Полигон распределения Запишем эмпирическую функцию распределения:  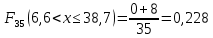  и т.д. и т.д.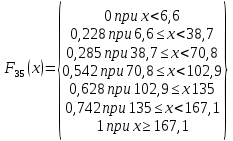 Найдём точечную оценку математического ожидания: 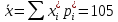 Точечная оценка дисперсии: Точечная оценка дисперсии: Точечная оценка среднеквадратичного отклонения: 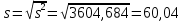 Построение доверительного интервала для математического ожиданияДоверительный интервал для математического ожидания имеет вид  (𝑥̅ − 𝑡 ∙ 𝑆 (𝑥̅ − 𝑡 ∙ 𝑆√𝑛 , 𝑥̅ + 𝑡 ∙ 𝑆 ).  √𝑛 √𝑛𝑥̅ = 105 𝑆 = 60,04 при доверительной вероятности γ=0,95 Ф(t)=0.975,откуда t=1.96. Получим: 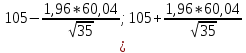  Таким образом, доверительный интервал для математического ожидания: 85,1 < 𝑚 < 124,9 Построение доверительного интервала для дисперсииДоверительный интервал для дисперсии 𝜎2 имеет вид   ((𝑛−1)𝑆2 , (𝑛−1)𝑆2 ). ((𝑛−1)𝑆2 , (𝑛−1)𝑆2 ).𝜒 2 𝛼,𝑛−1 𝜒2 𝛼 2 1−2,𝑛−1 𝑆2 = 3604,684 при доверительной вероятности γ=0,95 имеем 𝛼 = 1 − 𝛾 = 0,05, тогда значения хи-квадрат распределения: 𝜒2 2 2 2 𝛼,𝑛−1 = 𝜒0,025; 34 = 51.966; 𝜒 𝛼 = 𝜒0,925; 34 = 19.806. 2 1−2,𝑛−1 Получим: 34 ·3604,684  ( 51.966 , ( 51.966 ,34 · 3604,684  19.806 ) 19.806 )(2077,5; 5450,7). Таким образом, доверительный интервал для дисперсии: 2077,5 < 𝜎2 < 5450,7. Задача 2. Имеются две случайные величины Х1 и Х2. Необходимо установить между ними корреляционную связь, а также построить ковариационную матрицу. Данные для анализа представлены в таблице 2.1. Таблица 2.1
РешениеДля решения первой части решения задачи воспользуемся формулой Пирсона для коэффициента линейной корреляции малой выборки. Выполним расчёт необходимых величин при помощи exile данные сведем в таблицу. 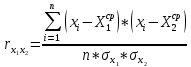 2.1 2.1Где; rx1x2- коэффициента линейной корреляции малой выборки xi-данные хср1 и хср2-среднее значение данных Ϭх1 и Ϭх2- стандартное отклонение х1 и х2 n-количество данных 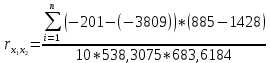 таблица 2.2
Проверка правильности решения при помощи функции коррел.  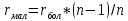 𝑋̅1 = −52,5; 𝑋̅2 = 446,6; 𝑋̅2 = 311770,9; 𝑋̅2 = 355579,2; 1 2 𝑋̅̅1̅̅𝑋̅̅2 = 4314,8. 𝑐𝑜𝑣(𝑋1, 𝑋1) = 𝜎2 = 𝑋̅2 − (𝑋̅1)2 = 311770,9 − (−52,5)2 = 309014,7 1 1 𝑐𝑜𝑣(𝑋1, 𝑋2) = 𝑐𝑜𝑣(𝑋2, 𝑋1) = 𝑋̅̅1̅̅𝑋̅̅2 − 𝑋̅1 · 𝑋̅2 = = 4314,8 − (−52,5) · 446,6 = 27761,3 𝑐𝑜𝑣(𝑋2, 𝑋2) = 𝜎2 = 𝑋̅2 − (𝑋̅2)2 = 355579,2 − 446,62 = 156127,6 2 2 Ковариационная матрица: 1 𝛺 = ( 𝜎2 𝑐𝑜𝑣(𝑋1, 𝑋2) ) = ( 309014,7 27761,3 ) 2 𝑐𝑜𝑣(𝑋2, 𝑋1) 𝜎2 27761,3 156127,6 Вычислим коэффициент корреляции: 𝑐𝑜𝑣(𝑋2, 𝑋1)  𝑟 = 𝑟 = √𝜎2𝜎2 27761,3  = = 0,126. = = 0,126.√309014,7 · 156127,6 1 2 Значение коэффициента корреляции положительное, это означает, что связь между X1 и X2 прямая: увеличению X1 соответствует увеличение X2. По модулю коэффициент корреляции находится в пределах от 0,1 до 0,3, поэтому можно сказать, что связь между X1 и X2 слабая. Вывод: между X1 и X2 наблюдается слабая прямая взаимосвязь.   | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
