задания олимпиады. Задания олимпиады. Задача Кирпичи для мостовой
 Скачать 108.08 Kb. Скачать 108.08 Kb.
|
|
7 КЛАСС Задача 1. «Кирпичи для мостовой». При производстве брусчатки для мощения улиц в Древнем Египте использовались каменные блоки размером 1×2×1 м, из которых каменотёсы делали брусчатку размером 10×10×20 см. Какую максимальную площадь удавалось египтянам замостить в день из N = 40 блоков, если α = 20% кирпичей крошились при распилке и не использовались? Ответ дать в квадратных метрах, округлив до целых. Толщина каменного тротуара 10 см. Зазоры на стыках не учитывать. Задача 2. «Поездка на дачу». Ваня поехал на дачу на велосипеде. На первой половине пути, который проходил сначала по асфальтированной дороге, Ваня ехал равномерно со скоростью, которая на 10 км/ч быстрее средней скорости. Вторую половину пути, проходившей по просёлочной дороге, он ехал со скоростью в полтора раза меньшей средней. Определите среднюю скорость Вани. Ответ выразить в км/ч, округлить до целых. Задача 3. «Противостояние Земли и Марса». В момент противостояния Солнце, Земля и Марс находятся на одной прямой (Земля между Солнцем и Марсом). Считая, что планеты обращаются вокруг Солнца по круговым орбитам, лежащим в одной плоскости, определите, через какой промежуток времени повторяются противостояния Земли и Марса. Планеты движутся в одну сторону. Марс совершает оборот вокруг Солнца за 687 земных дней, а Земля — за 365 дней. 8 КЛАСС Задача 1. «Валерьянка для Громозеки». Громозека — старый друг Алисы Селезневой, гигантский археолог с планеты Чумароза очень любит валерьянку. В стакан, заполненный на 2/3 его объема водой массы m1 = 200 г. Громозека накапал N одинаковых капель валерьянки объемом V0 = 0,2 мл каждая и аккуратно перемешал до однородной смеси. При этом уровень жидкости поднялся до краев стакана. Плотность воды 1 = 1,0 г/см3, плотности валерьянки 2 = 0,8 г/см3. Сколько примерно капель валерьянки накапал Громозека в стакан? Какова средняя плотность получившейся смеси? Утонет ли в этой смеси кубик льда плотностью 0 = 0,9 г/см3, который Громозека положил в стакан? 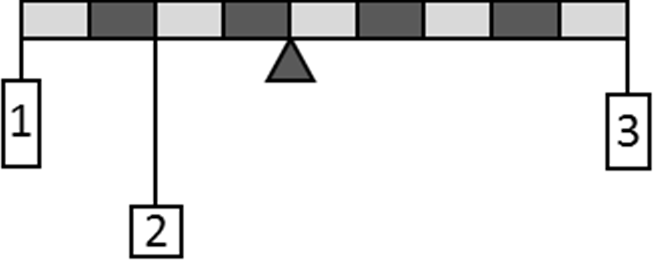 Задача 2. «Три груза». На рисунке показан рычаг массой M = 18 кг, к которому в разных местах прикреплены три груза. Масса первого груза равна m, масса второго в a = 2 раза больше, а масса третьего в b = 3 раза меньше. Чему равна масса m, если система находится в равновесии? Ответ выразить в килограммах, округлив до десятых. Задача 2. «Три груза». На рисунке показан рычаг массой M = 18 кг, к которому в разных местах прикреплены три груза. Масса первого груза равна m, масса второго в a = 2 раза больше, а масса третьего в b = 3 раза меньше. Чему равна масса m, если система находится в равновесии? Ответ выразить в килограммах, округлив до десятых. Найдите скорость течения реки и скорость катера в стоячей воде, считая эти скорости постоянными. В какой момент времени катер прибыл в Березовку? Постройте зависимость расстояния до Орловки от времени для плота и катера на одном графике. Задача 4. «Весна пришла» На крыше дома лежала глыба льда при температуре t1 = −t °C. Днём весеннее солнышко растопило весь лёд, превратив его в воду при температуре t2 = +2t °C. На весь этот процесс была затрачена теплота в количестве Q = 12 МДж, причём известно, что 1/3 от этого количества теплоты пошла на нагревание воды. Также известно, что удельная теплоёмкость льда в 2 раза меньше удельной теплоёмкости воды. Определите количество теплоты, которое пошло на превращение льда в воду. Ответ выразить в кДж. Если ответ не целый, то округлить до целых. 9 КЛАСС 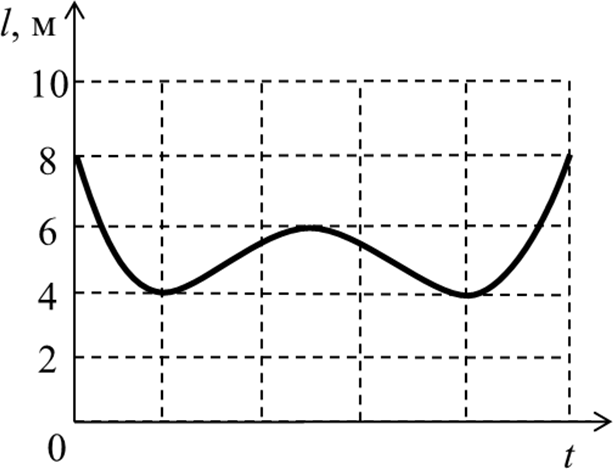 Задача 1. «Взгляд со стороны» Тело бросили вертикально вверх с поверхности земли. Расстояние l между этим телом и неподвижным наблюдателем изменяется со временем t по закону, показанному на графике (см. рисунок). Ускорение свободного падения g = 10 м/c2. Задача 1. «Взгляд со стороны» Тело бросили вертикально вверх с поверхности земли. Расстояние l между этим телом и неподвижным наблюдателем изменяется со временем t по закону, показанному на графике (см. рисунок). Ускорение свободного падения g = 10 м/c2.На какой высоте над землёй и на каком расстоянии от линии, по которой движется тело, находится наблюдатель? Чему равна начальная скорость тела? Задача 3. «Утренний чай». Утром, перед тем, как пойти в школу, Маша налила себе чай. Плотность чая равна плотности воды: ρв = 1000 кг/м3. Потом Маша насыпала в чай сахар. Плотность сахара равна ρс = 1,6 г/см3. Потом Маша размешала сахар в чаю. После этого объём чая стал в n = 1,04 раза больше, чем до добавления сахара, а плотность чая стала равна ρч = 1060 кг/м3. Какой была средняя плотность чая, когда Маша положила в него сахар, но ещё не размешала? 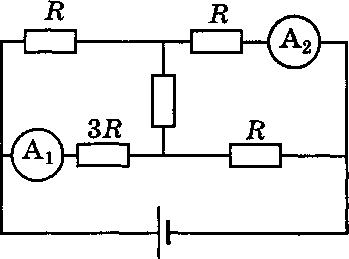 Задача 4. «Два амперметра». Во время лабораторной работы школьники собрали электрическую цепь в соответствии со схемой, показанной на рисунке. Амперметр А1 показывает силу тока I1 = 2 A. Какую силу тока показывает амперметр А2? Оба прибора идеальны. Отмеченные на рисунке параметры цепи считайте известными. Задача 4. «Два амперметра». Во время лабораторной работы школьники собрали электрическую цепь в соответствии со схемой, показанной на рисунке. Амперметр А1 показывает силу тока I1 = 2 A. Какую силу тока показывает амперметр А2? Оба прибора идеальны. Отмеченные на рисунке параметры цепи считайте известными.  Задача 5. «Лазерная указка». Два зеркала сложены под углом = 7º. Школьник Станислав направил через маленькое отверстие в одном из зеркал луч лазерной указки перпендикулярно этому зеркалу. Сколько всего отражений испытает луч от этих зеркал? Задача 5. «Лазерная указка». Два зеркала сложены под углом = 7º. Школьник Станислав направил через маленькое отверстие в одном из зеркал луч лазерной указки перпендикулярно этому зеркалу. Сколько всего отражений испытает луч от этих зеркал? 10 КЛАСС Задача 1. «По дороге в школу». Варя ездит в школу на метро. Однажды, наблюдая за приближением поезда, она с помощью секундомера определила, что первый вагон прошёл мимо неё за время t1 = 2 с, а второй вагон – за время t2 = 2,1 с. Когда мимо Вари проходил последний вагон, поезд остановился. Сколько времени прошло того момента, когда поезд начал проходить мимо Вари до полной его остановки? Сколько вагонов в поезде? Все вагоны имеют одинаковую длину, промежутками между вагонами пренебречь. Считать, что измерения, сделанные Варей точны, а поезд, подходящий к станции, движется равнозамедленно. Задача 2. «Ванна Архимеда» 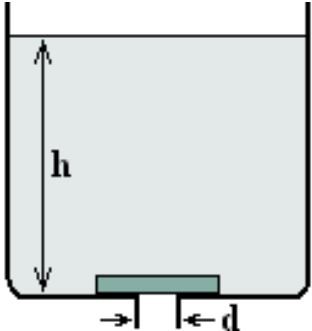 . В ванну налили воду до уровня h = 40 см и положили на сливное отверстие стеклянный брусок, масса которого равна m = 640 г. Диаметр сливного отверстия d = 4 см. Вода подтекает под брусок, но очень медленно. Уровень воды не изменится долго. С какой силой брусок давит на дно ванны? Плотность воды ρв =1000 кг/м3, плотность стекла ρс = 2500 кг/м3. Ускорение свободного падения g = 10 м/c2. Атмосферным давлением пренебречь. Ответ запишите в единицах СИ с точностью до десятых. Задача 3. «Переохлаждённая жидкость». Как известно, при атмосферном давлении вода начинает замерзать, а лёд - таять при температуре t = 0°C. Но при соблюдении необходимых предосторожностей вода может быть переохлаждена до более низких температур. Какая часть переохлаждённой до температуры t0 = -4С воды замёрзнет, если бросить в неё ледяную сосульку и вызвать тем самым кристаллизацию? Удельная теплота плавления льда λ = 335∙103 Дж/кг, теплоемкость воды cв = 4200 Дж/кг∙С, удельная теплоемкость льда cл = 2100 Дж/кг∙С. Потерями теплоты пренебречь. Задача 4. «Последовательное соединение». Связь между напряжением U на лампе накаливания и силой тока, текущего через неё, даётся формулой I ∼ U3/5. Две лампы с номинальными напряжениями 220 В и номинальными мощностями P1 = 40 Вт и P2 = 100 Вт включили последовательно в сеть 220 В. Какое напряжение падает на лампе меньшей номинальной мощности? Задача 5. «Столкновение на орбите». Искусственный спутник Луны массой M = 8 кг движется вблизи её поверхности по круговой орбите. Метеорит массой m = 0,1 г, летящий со скоростью v = 40 км/с, перпендикулярной скорости спутника, попадает в спутник и застревает в нём. На какой угол повернётся из-за этого вектор скорости спутника? Радиус Луны R = 1740 км. Ускорение свободного падения на Луне в 6 раз меньше, чем на Земле. . В ванну налили воду до уровня h = 40 см и положили на сливное отверстие стеклянный брусок, масса которого равна m = 640 г. Диаметр сливного отверстия d = 4 см. Вода подтекает под брусок, но очень медленно. Уровень воды не изменится долго. С какой силой брусок давит на дно ванны? Плотность воды ρв =1000 кг/м3, плотность стекла ρс = 2500 кг/м3. Ускорение свободного падения g = 10 м/c2. Атмосферным давлением пренебречь. Ответ запишите в единицах СИ с точностью до десятых. Задача 3. «Переохлаждённая жидкость». Как известно, при атмосферном давлении вода начинает замерзать, а лёд - таять при температуре t = 0°C. Но при соблюдении необходимых предосторожностей вода может быть переохлаждена до более низких температур. Какая часть переохлаждённой до температуры t0 = -4С воды замёрзнет, если бросить в неё ледяную сосульку и вызвать тем самым кристаллизацию? Удельная теплота плавления льда λ = 335∙103 Дж/кг, теплоемкость воды cв = 4200 Дж/кг∙С, удельная теплоемкость льда cл = 2100 Дж/кг∙С. Потерями теплоты пренебречь. Задача 4. «Последовательное соединение». Связь между напряжением U на лампе накаливания и силой тока, текущего через неё, даётся формулой I ∼ U3/5. Две лампы с номинальными напряжениями 220 В и номинальными мощностями P1 = 40 Вт и P2 = 100 Вт включили последовательно в сеть 220 В. Какое напряжение падает на лампе меньшей номинальной мощности? Задача 5. «Столкновение на орбите». Искусственный спутник Луны массой M = 8 кг движется вблизи её поверхности по круговой орбите. Метеорит массой m = 0,1 г, летящий со скоростью v = 40 км/с, перпендикулярной скорости спутника, попадает в спутник и застревает в нём. На какой угол повернётся из-за этого вектор скорости спутника? Радиус Луны R = 1740 км. Ускорение свободного падения на Луне в 6 раз меньше, чем на Земле. 11 КЛАСС Задача 1. «Воздушный шарик». Наполненный гелием воздушный шарик имеет форму, близкую к сферической. Если отпустить его в безветренную погоду, скорость его установившегося (то есть равномерного) подъёма будет равна u0 = 2 м/с. Этот шарик привязали к багажнику велосипеда. Когда велосипедист на этом велосипеде ехал навстречу ветру со скоростью u = 1 м/c относительно земли, нить шарика отклонилась от вертикали на постоянный угол. Найдите этот угол, если скорость ветра равна u= 0,5 м/c. Считать, что при движении шарика в воздухе величина действующей на него силы сопротивления пропорциональна квадрату его скорости относительно воздуха. Задача 2. «Полет на ядре». Пушка массы М = 200 кг стреляет ядром массы mя = 20 кг под утлом α = 30º к горизонту. Заряд пороха mп = 5 кг, его теплота сгорания q = 3,8 МДж/кг. Определите расстояние между пушкой и местом взрыва, если они находятся на одной горизонтали. На сколько уменьшится дальность полёта ядра, если сразу после вылета из пушки на него сядет барон Мюнхгаузен, масса которого m = 70 кг? КПД выстрела принять равным 10%. Считать, что пушка находится на гладкой поверхности, по которой может скользить без трения. Сопротивлением воздуха пренебречь. Ускорение свободного падения g = 10 м/c2. 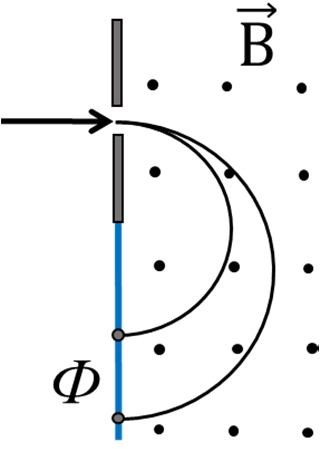 . В масс-спектрографе - устройстве для определения изотопного состава однозарядные ионы калия с атомными весами A1 = 39 и A2 = 41 сначала ускоряются в электрическом поле, а затем через узкую щель попадают в однородное магнитное поле, перпендикулярное к направлению их движения (рис.). В процессе опыта из-за несовершенства аппаратуры ускоряющий потенциал электрического поля меняется около среднего значения U на величину ±ΔU. С какой относительной точностью ΔU/U нужно поддерживать значение ускоряющего потенциала, чтобы пучки изотопов калия при попадании на фотопластинку Ф не перекрывались? . В масс-спектрографе - устройстве для определения изотопного состава однозарядные ионы калия с атомными весами A1 = 39 и A2 = 41 сначала ускоряются в электрическом поле, а затем через узкую щель попадают в однородное магнитное поле, перпендикулярное к направлению их движения (рис.). В процессе опыта из-за несовершенства аппаратуры ускоряющий потенциал электрического поля меняется около среднего значения U на величину ±ΔU. С какой относительной точностью ΔU/U нужно поддерживать значение ускоряющего потенциала, чтобы пучки изотопов калия при попадании на фотопластинку Ф не перекрывались? |
