Комбинаторика. Дискретная математика. Задача на формулу произведения. Условие
 Скачать 22.2 Kb. Скачать 22.2 Kb.
|
|
Задача на формулу произведения. Условие: Мальчик разбил лист А3 на 7 частей разных размеров и в этих частях решил нарисовать какое-то мифическое существо. Изучив информацию о некоторых из них, он определил, что в 1 части листа можно нарисовать 6 видов существ, во 2 части – 12 видов, в 3 части – 2, в 4 части – 4, в 5 и 6 части – 3, в 7 части – 10. Сколько рисунков может получиться, если мальчик в каждой части должен нарисовать какое-либо мифическое существо? Решение: Пусть часть 1 – A1=6, часть 2 – A2 =12, часть 3 – A3=2, часть 4 – A4=4, часть 5 – A5=3, часть 6 – A6=3, часть 7– A7=10. Так как рисунки отличаются, даже если поменялось лишь мифическое существо в 1 части(то есть все части связаны между собой), то для подсчёта количества возможных рисунков используем формулу произведения. 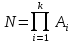 , где k – количество частей. , где k – количество частей.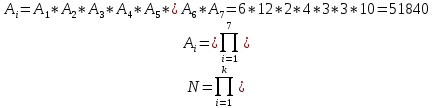 Ответ: 51840 рисунков. Задача на формулу сложения. Условие: Лена решила поставить один из предметов (или одну из групп предметов) на свой рабочий стол. Стопку тетрадей она может положить в 6 мест на столе, поставить лампу – в 4 различных места, поставить принтер – в 2 места, положить пенал с канцелярскими приборами – в 21 место. Сколько существует способов занять стол? Решение: Пусть количество расположений стопки тетрадей – A1=6, количество расположений лампы – A2=4, количество расположений принтера– A3=2, количество расположений пенала – A4=21. Так как действия не связаны между собой, то общее количество вариантов будет вычисляться по формуле суммы 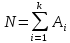 , где k – количество вещей и равно 4. , где k – количество вещей и равно 4.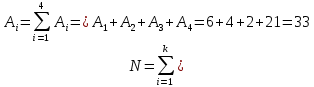 Ответ: 33 варианта. Задача на формулы включения-исключения. Условие: 41 фирма выпускает ручки 3 вариантов: чёрные, синие и цветные, причём каждая фирма производит хотя бы 1 вид ручек. Синие ручки выпускают 27 фирм, черные ручки – 22 фирм, цветные – 18 фирм. Черные и синие ручки выпускает 12 фирм, черные и цветные – 9 фирм, а синие и цветные – 7 фирм. Сколько фирм выпускают ручки всех 3 вариантов? Решение: Так как у нас есть три пересекающихся друг с другом множества, то для нахождения количества фирм, изготавливающих каждый вид ручек, нужно воспользоваться формулой включения-исключения. Обозначим за Aч – общее количество фирм с чёрными ручками, равное 22, Aс – количество фирм с синими ручками, равное 27, Aц– количество фирм с цветными ручками, равное 18, Aчс – количество фирм с чёрными и синими ручками, равное 12, Aчц – количество фирм с чёрными и цветными ручками, равное 9, Aсц – количество фирм с синими и цветными ручками, равное 7, Aчсц – количество фирм со всеми видами ручек(необходимо найти), а А – количество фирм и равно 43. Тогда формула приобретает вид: 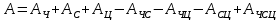 , откуда: , откуда: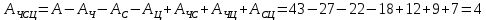 Ответ: 4 фирмы. Задача на размещение. Условие: Мальчик раскрашивает последовательно прямоугольник, ромб, квадрат, круг, треугольник и шестиугольник. У него есть 24 цветных карандаша, цвет каждого карандаша не повторяется. Сколькими способами можно раскрасить 6 перечисленных фигур, если цвета каждой фигуры также не повторяются? Решение: Мы должны выбрать 6 цветов из 24, чтобы раскрасить предоставленные нам фигуры. Однако, так как каждая фигура – разная, то последовательности цветов для раскраски 6 перечисленных фигур также будут различаться ( к примеру, обозначим цвета синий – с, зелёный – з, фиолетовый – ф, голубой – г, красный – к, жёлтый – ж. Последовательность сзфгкж будет отличаться от последовательности зсфгкж, которая отличается от фзсгкж и т.д.). Следовательно, чтобы посчитать количество способов раскраски мы должны воспользоваться формулой размещения 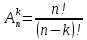 , где n – общее количество цветов, k – необходимое количество цветов для раскрашивания фигур. , где n – общее количество цветов, k – необходимое количество цветов для раскрашивания фигур. 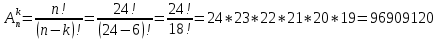 Ответ: 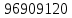 способов. способов.Задача на перестановки. Условие: Художник выстраивает рядом с мольбертом последовательно баночки с краской 24 различных цветов. Сколько существует возможных вариантов расстановок красок? Решение: Разобьём последовательность на 24 позиции. На 1 позицию можно поставить 24 баночки, но уже на 2 позицию – 23 баночки(24-ая стоит на 1 позиции), на 3 – 22 баночки и т.д. Из этого можно сделать вывод, что общее число возможных вариантов мы можем посчитать по формуле перестановок 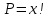 , где x – количество баночек с краской. , где x – количество баночек с краской.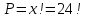 Ответ: 24! Задача на сочетание. Условие: Мальчик раскрашивает 6 одинаковых фигур. У него есть 24 цветных карандаша, цвет каждого карандаша не повторяется. Сколькими способами можно раскрасить фигуры, если цвета каждой фигуры также не повторяются? Решение: Мы должны выбрать 6 цветов из 24, чтобы раскрасить предоставленные нам фигуры. Так как каждая фигура – одинаковая, то нам неважно, в какой последовательности будут выбранные цвета. Следовательно, чтобы посчитать количество способов раскраски мы должны воспользоваться формулой размещения 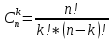 , где n – общее количество цветов, k – необходимое количество цветов для раскрашивания фигур. , где n – общее количество цветов, k – необходимое количество цветов для раскрашивания фигур. 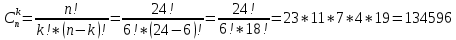 Ответ: 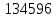 способов. способов.Задача на разбиение. Условие: Художественной школе поручили заняться подготовкой к мероприятию. Ребята решили нарисовать 5 картин, 3 из которых они повесят напротив и по бокам относительно главного входа, 1 повесят рядом с актовым залом и 1 – в классе, где проводятся сами занятия. Всего в художественной школе 43 человека. На 1 картину нужно выделить 12 человек, на 2 и 3 – по 10 человек, на 4 картину – 7 человек и на 5 картину – 4 человека. Сколькими способами можно распределить людей? Решение: Сумма всех людей, требующихся для работы над всеми картинами = 12+10+10+7+4 =43, что равно общему количеству всех обучающихся в художественной школе. Так как нужно разделить больное множество всех людей на 5 групп по определённому количеству человек(пусть будет число km. k1=12, k2=10, k3=10, k4=7, k5=4), то нужно воспользоваться формулой разбиения 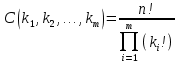 . .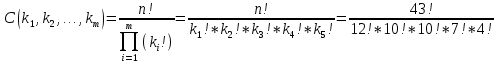 Ответ: 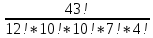 способов. способов. |
