Математическое моделирование. КР. Кузьменко АИ. Задача Приведите примеры определений математического моделирования с ссылкой на авторов. Обоснуйте, почему определения сильно отличаются друг от друга
 Скачать 135.73 Kb. Скачать 135.73 Kb.
|
|
Задача 1. Приведите примеры определений математического моделирования с ссылкой на авторов. Обоснуйте, почему определения сильно отличаются друг от друга. Согласно определению Горностаевой Т.Н., математическое моделирование – это метод научного познания действительности с помощью построения математических моделей и проведения с ними теоретического исследования (эксперимента). По А.А. Ляпунову, математическое моделирование - это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель), находящаяся в некотором объективном соответствии с познаваемым объектом, способная замещать его в определенных отношениях и дающая при ее исследовании, в конечном счете, информацию о самом моделируемом объекте. Коржов Е.Н. в своем методическом пособии дает следующее определение: математическая модель – это образ или отображение реального объекта, построенный с помощью математических соотношений, которые устанавливают связи между определяющими свойствами объекта (уравнения, неравенства). Я думаю, что сильное отличие в определении этого понятия заключается в следующем: Во-первых, технологии развиваются так быстро, что постоянно появляется новое наполнение термина, которое не всегда стыкуется с предыдущими толкованиями. В данном случае определения выдвигались авторами с промежутков в 10-30 лет. Во-вторых, на сегодняшний день математическое моделирование применяются во многих отраслях современной науки. Математические модели являются инструментом описания самых разных задач и применяются в различных областях человеческой деятельности: образовании, научно-исследовательской деятельности, техническом проектировании, механике, медицине, экономике, экологии и т.д. Поэтому, в зависимости от отрасли применения математического моделирования, определение данного понятия может варьироваться и не совпадать. Задача 2. Определите методы моделирования показателей бухгалтерского баланса. Метод детерминированного факторного анализа применяется при расчете показателей основных средств, отложенных налоговых активов, запасов. Также в бухгалтерском учёте применяются такие методы, как метод многокритериальной оптимизации и метод пропорциональных зависимостей показателей Задача 3. Модели не бывают универсально адекватными, они разрабатываются для конкретных целей. Приведите пример неадекватности модели. Верно ли утверждение, что адекватная модель – точная. Адекватность (от лат. adaequatus — приравненный) — соответствие модели моделируемому объекту (оригиналу) или процессу. Адекватность в какой-то мере условное понятие, так как полного соответствия модели реальному объекту быть не может, иначе это была бы не модель, а сам объект. При моделировании имеется в виду адекватность не вообще, а по тем свойствам модели, которые для исследования считаются существенными. Говорят, что модель адекватна оригиналу, если при ее интерпретации возникает «портрет», в высокой степени сходный с оригиналом. До тех пор, пока не решен вопрос, правильно ли отображает модель исследуемую систему (т.е. адекватна ли она), ценность модели нулевая. Задача 4. Решите задачу о кратчайшем пути. Каким кратчайшим путем можно попасть из подразделения № 1 в подразделение № 4 (таблица 1)? Таблица 1 – Исходные данные 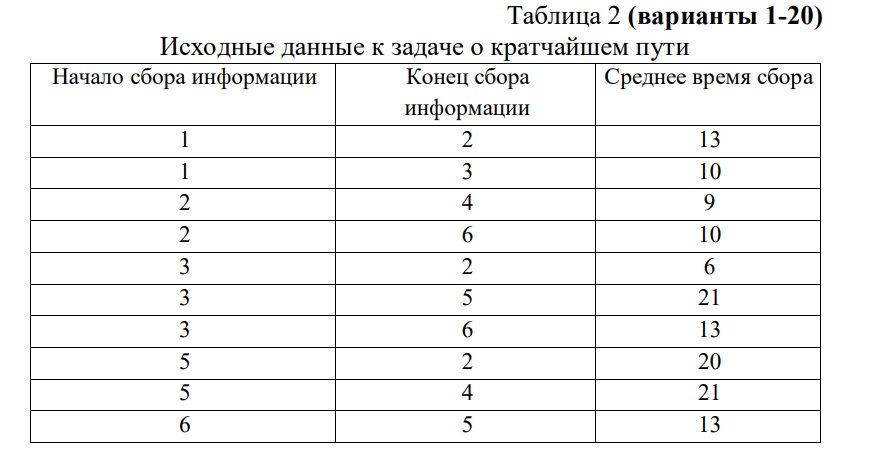 Решение: Составим ориентированный граф: 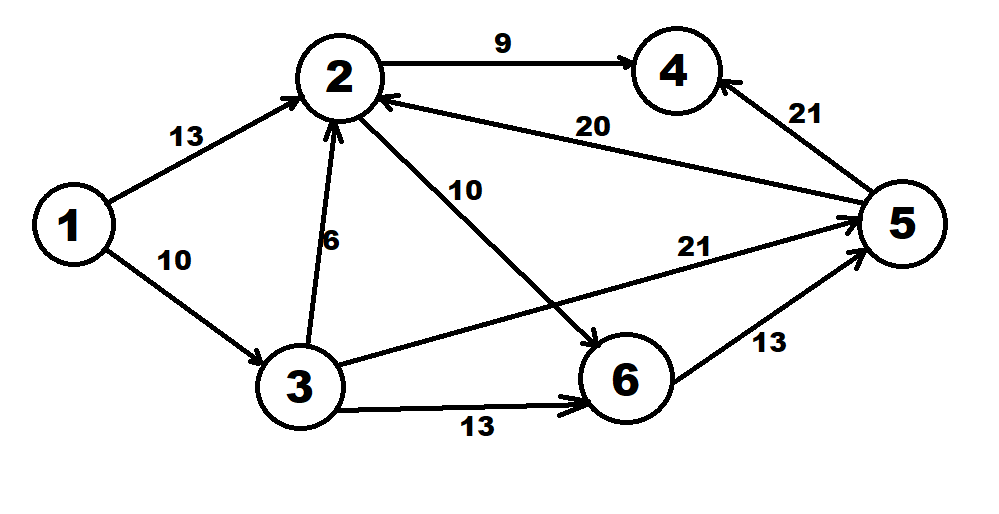 Введем обозначение: С(Т) – длина кратчайшего пути из вершины 1 в вершину Т. Рассматриваемая задача состоит в вычислении С(4) и указании пути, на котором этот минимум достигается. Для исходных данных, представленных в графе и в таблице 1, вершину 3 входит только одна стрелка, как раз из вершины 1, и около этой стрелки стоит ее длина, равная 10, поэтому С (3) = 10. Кроме того, очевидно, что С (1) = 0. В вершину 4 можно попасть либо из вершины 2, пройдя путь, равный 9, либо из вершины 5, пройдя путь, равный 21, поэтому справедливо соотношение: С(4) = min {С(2) + 9; С(5) + 21}. Таким образом, проведено упрощение задачи, нахождение С(4) сведено к нахождению С(2) и С(5). В вершину 5 можно попасть либо из вершины 3, пройдя путь, равный 2, либо из вершины 6, пройдя путь, равный 3, поэтому справедливо соотношение: С(5) = min {С(3) + 21; С(6) + 13}. Известно, что С(3) = 10, поэтому С(5) = min {31; С(6) + 13}. Поскольку очевидно, что С(6) – это положительное число, то из последнего соотношения вытекает, что С(5) = 31. В вершину 2 можно попасть либо из вершины 1, пройдя путь, равный 13, либо из вершины 3, пройдя путь, равный 6, либо из вершины 5, пройдя путь, равный 21. Поэтому справедливо соотношение: С(2) = min {С(1) + 13; С(3) + 6; С(5) + 20}. Нам известно, что С(1) = 0, С(3) = 10, С(5) = 31, поэтому С(2) = min {0 + 13; 10 + 6; 31 + 20} = min {13; 16; 51} = 51. Теперь мы можем найти С(4): С(4) = min {С(2) + 9; С(5) + 21} = min {13 + 9; 31 + 21} = min {22; 52} = 22. Таким образом, длина кратчайшего пути равна 22. Из последнего соотношения ясно, что в вершину 4 надо идти через вершину 2. Возвращаясь к вычислению С(2), видим, что в вершину 2 надо идти через вершину 1. Итак, кратчайший путь таков: 1 → 2 → 4. Ответ: кратчайший путь: 1 → 2 → 4. Задача 5. (варианты 1-100) Составьте анкету о вреде курения. Выделите альтернативы, типы вопросов. Проведите опрос в группе. Определите согласованность мнений одногруппников Анкета представлена в отдельном файле «Анкета». Задача 6. (варианты 1-100) Дайте интерпретацию математической модели: Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции. Она имеет вид: 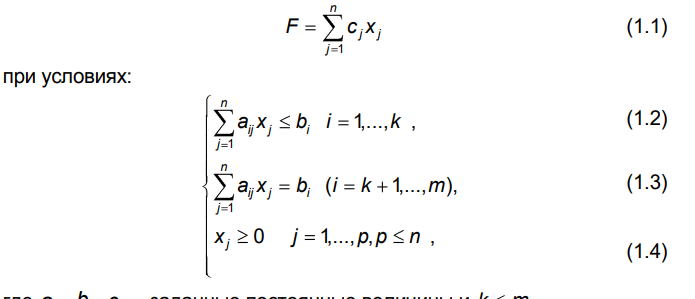 При условиях: 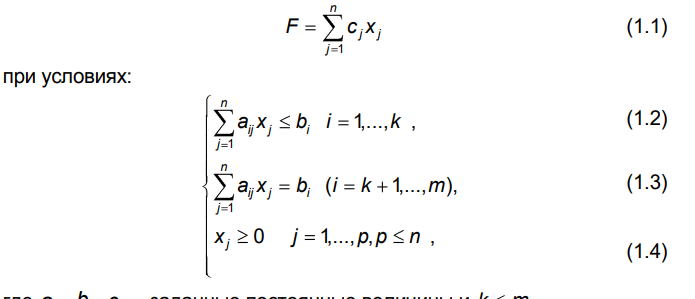 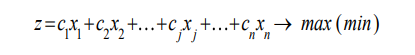 Задачи линейного программирования в канонической форме имеет вид: Задачи линейного программирования в канонической форме имеет вид:(1.1) при условиях: 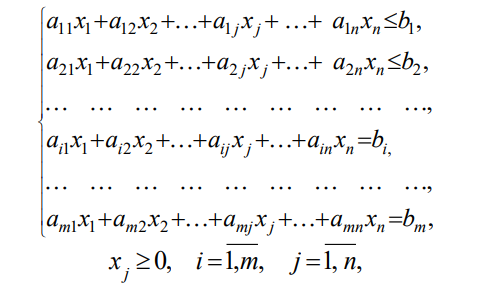 (1.2) где xj – неизвестные; aij, bi, cj – заданные постоянные величины, z = z (x1, x2 ,…, xn) – целевая функция Функция (1.1) называется целевой функцией (или линейной формой) задачи, а условия (1.2) – ограничениями данной задачи. Чтобы перейти от одной формы записи задачи линейного программирования к другой, нужно в общем случае уметь, во-первых, сводить задачу минимизации функции к задаче максимизации, вовторых, переходить от ограничений-неравенств к ограничениям-равенствам и, наоборот, в-третьих, заменять переменные, которые не подчинены условию неотрицательности. В том случае, когда требуется найти минимум функции 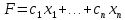 можно перейти к нахождению максимума функции можно перейти к нахождению максимума функции 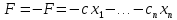 поскольку поскольку 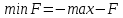 Ограничение-неравенство исходной задачи линейного программирования, имеющее вид ≤, можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида ≥ – в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Например, ограничение-неравенство 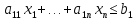 преобразуется в ограничение-равенство преобразуется в ограничение-равенство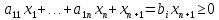 а ограничение-неравенство 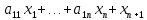 ≥ b1 – в ограничение-равенств ≥ b1 – в ограничение-равенств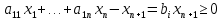 В то же время каждое уравнение системы ограничений можно записать в виде неравенств: 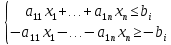 Количество вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно количеству преобразуемых неравенств. Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объему неиспользуемого соответствующего ресурса. |
