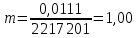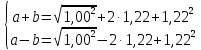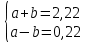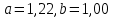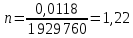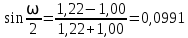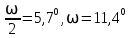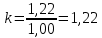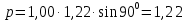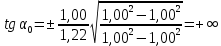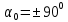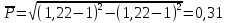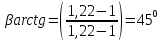Задание 2. Задание 2 Вычисление размеров искажений
 Скачать 370.06 Kb. Скачать 370.06 Kb.
|
Задание 2: Вычисление размеров искаженийЦель задания. Изучить способы определения размеров искажений на картах, научиться понимать характер распределения искажений в картографических проекциях, получить навыки построения эллипсов искажений и оценки через их размеры и форму характера и величин искажений. Выполнение задания. Для трех точек с указанными географическими координатами φ и λ из приведенных ниже вариантов заданий определить следующие величины: масштаб площади p; наибольший aи наименьший bмасштабы; максимальное искажение угла ω; искажение форм k; направление наибольшего частного масштаба α0; величину вектора и его направление β. Определение произвести, пользуясь формулами: 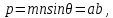 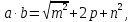 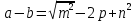 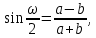 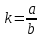 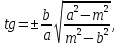 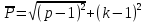 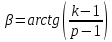 и картами с изоколами. Для каждой точки сделать выкопировку эллипса искажений и вектора 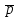 . .Исходные материалы. Варианты картографических проекций с изоколами (прил. 2), географические координаты φ и λ трех точек, карандаш, ластик, циркуль- измеритель, линейка, транспортир, калькулятор, таблица длин одноградусных дуг параллелей и меридианов на эллипсоиде Красовского (прил. 3), таблицы тригоно- метрических функций (прил. 4), калька, листинг программы для автоматизированного расчета величин искажений (прил. 5). Указания к выполнению задания. При определении искажений в точке с заданными координатами φи λна первом этапе следует найти частные масштабы по меридиану mи параллели n. Для этого с помощью циркуля-измерителя и линейки определяют по карте (с точностью до 0,1 мм) длины отрезков касательных к меридиану l1 и параллели l2, на которых лежит данная точка. Измерения производятся по меридиану к северу и к югу, по параллели – к востоку и западу до соседних к данной точке параллелей и ме ридианов соответственно (рис.21). касательная к меридиану 170 150 50 l2 130 θ 110 90 70 50 30 150 l1 130 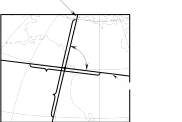 110 110касательная к параллели 30 Масштаб 1 : 100 000 000 Рис. 21. Схема определения длин касательных к меридиану l1 и параллели l2, а также угла θ между ними на карте. Соответствующие им длины на эллипсоиде L1 и L2 берутся из приложения 3. Частные масштабы по меридиану mи параллели nвыражаются в долях главного с точностью до 0,01 по формулам: m l1 L1 n l2 L2 M, M, где M– знаменатель главного масштаба карты. Измерить с помощью транспортира острый угол θ между касательными к меридиану и параллели в данной точке с точностью до 0,1 (рис. 21). Вычислить с помощью калькулятора и таблиц тригонометрических функций (прил. 4) по приведенным выше формулам величины p, a, b, k, с точностью до 0,01 и ω, α0, βс точностью до 0,1. Определить величины pи ω, пользуясь картографической сеткой предложенной проекции с изоколами путем интерполирования (прил. 2) Для величин p и ωпо двум определениям найти средние арифметические значения. Сделать выкопировку участка карты с данной точкой и показать эллипс искажений. Вычертить вектор для заданной точки. Результаты работы оформляются в виде таблицы 11. Пример выполнения задания. Определить величины искажений для точки с координатами 30 с.ш. и 20в.д. для карты 1 приложения 2. Карта составлена в нормальной азимутальной равнопромежуточной проекции Постеля на касательной плоскости, следовательно искажения всех видов отсутствуют в центральной точке, совпадающей с Северным полюсом, длины сохраняются вдоль всех меридианов (т.е. m = 1), а изоколы имеют вид окружностей. Длины отрезков касательных к меридиану l1 и параллели l2 в данной точке, измеренные с точностью до 0,1 мм, равны 1,11 и 1,18 см соответственно. Поскольку картографическая сетка ортогональна, угол пересечения меридианов и параллелей равен 90,0. Определение соответствующих отрезкам l1 и l2 на карте длин на земном эллипсоиде L1 и L2 следует проводить по таблице длин одноградусных дуг параллелей и меридианов на эллипсоиде Красовского (прил. 3). Отрезок l1, заключенный между 40 и 20 широты, на земном эллипсоиде равен разнице между расстояниями по меридиану от экватора до параллелей 40 и 20 (рис. 22а): первое расстояние равно 4 429 607 м, второе – 2 212 406 м, разница между ними – L1 – 2 217 201 м1. Отрезок l2 соответствует расстоянию по 30-ой параллели в 20 долго- ты (30 – 10 в.д.); 1 30-ой параллели имеет длину 96 488 м, а 20 – L2 – 1 929 760 м (рис. 22б). Для вычисления частных масштабов mи nнеобходимо перевести величины l1,l2,L1 иL2 в одни единицы измерения: 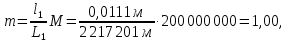
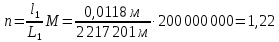 Полученные значения свидетельствуют о сохранении главного масштаба длин вдоль меридиан и преувеличении длин вдоль параллели на 22%. Далее по формулам определяем все требуемые показатели: 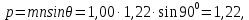 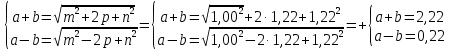 2a = 2,44, a = 1,22, b = 1,00 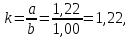 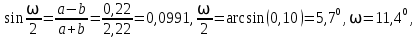 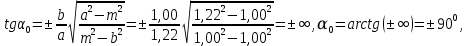 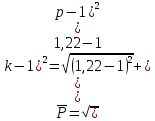 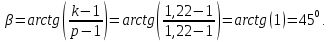 По карте изокол (карта 1 прил.2) путем интерполирования определяем, что величина искажения площади р в точке 300с.ш. и 200в.д. равна 1,22, а величина искажения угла ⍵ - 11,00. Таким образом, среднее значение искажения площадей и углов по трем измерениям составляет: 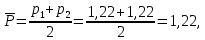 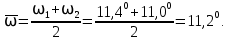 Расхождения в значениях величин, определяемых различными способами, могут возникать за счет ошибок округления, неточностей измерений или интерполирования. Полученные значения подтверждают равнопромежуточные свойства проекции: m= 1,00, = 45. Площади бесконечно малых фигур в данной точке преувеличиваются на 22 %, а максимальное расхождение углов на карте и на эллипсоиде составляет 11,2. Направление наибольшего частного масштаба a совпадает с направлением параллели (0 = 90), экстремальные частные масштабы равны частным масштабам по меридиану и параллели (a = n, b = m). Точка лежит в области умеренных искажений. Судя по форме и величине эллипса искажений деформации изображения исходной земной поверхности проявились в его растяжении в субширотном направлении. Результаты работы представляются в виде таблицы 11. Таблица 11 Форма представления результатов вычислений размеров искажений Нормальная азимутальная равнопромежуточная проекция Постеля масштаба 1 : 200 000 000 (Северное полушарие)
Для построения эллипса искажений на касательных к меридиану и параллели от заданной точки в обоих направлениях откладываются величины частных масштабов m и n соответственно из расчета в 1 см радиуса эллипса – 1 единица частного масштаба длин. Далее от касательной к меридиану в направлении полюса откладывается угол 0 – направление наибольшего частного масштаба a, к которому в заданной точке восстанавливается перпендикуляр – направление наименьшего частного масштаба b. На построенных направлениях откладываются величины aи b (рис. 23а). В целях уточнения построений можно воспользоваться формулой [8] для получения промежуточных значений радиусов эллипса. Засечки расстояний соединяются плавной линией (рис. 23б). В заданной точке пунктирной линией радиусом 1,00 вычерчивается исходная окружность. Вектор строится в соответствии с рисунком 8 по рассчитанным значениям направления вектора и его скалярной величины.  а) касательная к меридиану б) а) касательная к меридиану б)170 150 130 110 90 70 170 150 130 110 90 70 0 ma 50 50 b n50 50 b касательная к параллели am 30 150 130 30 110 30 150 130 30 110 Масштаб: 1 см радиуса эллипса искажений = 1 ед. частного масштаба длин Рис. 23. Схема построения эллипса искажений: откладывание длин m = 1,50, n = 0,75, a = 1,55 и b = 0,71 в заданных направлениях (а) и соединение отмеченных засечек до получения эллипса (б). Пунктирной линией показана исходная (недеформированная) окружность радиусом 1,00. Форма и величина эллипса показывают, что при разворачивании криволинейной земной поверхности в плоскость (т.е. при использовании картографической проекции) в точке = 50 с.ш. и = 130 з.д. произошло сжатие изображения в субширотном направлении на 25 % и растяжение его в субмери- диональном направлении на 50 %. Экстремальные (наименьшая и наибольшая) величины сжатия и растяжения в этой точке равны 29 и 55 % соответственно. Сроки выполнения и оценка работы. Работа рассчитана на 2 практических занятия. Результаты работы оцениваются 7 баллами: для каждой из трех точек начисляется по полбалла за верно рассчитанные значения искажений p, k, и вектора ; одним баллом оценивается общее качество оформления рисунков. Варианты заданий
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||