физика. физика вопросы. Закон Ньютона Третий закон Ньютона гласит Сила, действующая со стороны первого тела на второе, равна по величине и противоположна по направлению силе, действующей со стороны второго тела на первое
 Скачать 75.98 Kb. Скачать 75.98 Kb.
|
|
9. Третий закон Ньютона Третий закон Ньютона гласит: Сила, действующая со стороны первого тела на второе, равна по величине и противоположна по направлению силе, действующей со стороны второго тела на первое:
Ниже мы увидим, что при очень больших скоростях движения тел третий закон в сформулированном выше виде не будет выполняться, так как в таких ситуациях необходимо будет учитывать конечную скорость передачи взаимодействия (она не может быть выше скорости света). Ситуация, когда не выполняется третий закон Ньютона, типична также для тех случаев, когда рассматривается взаимодействие материальной точки с силовым полем: на точку со стороны поля сила действует, а противодействующей силы, приложенной к другому телу, нет. Третий закон (3.3) обеспечивает процедуру измерения силы. Так, например, динамометр показывает силу, с которой тело растягивает его пружину, но одновременно мы должны считать, что именно с такой же по величине силой пружина действует на тело. Вторая сила является как бы реакцией на первую, как показано на рис. 3.1. Ее иногда так и называют силой реакции. 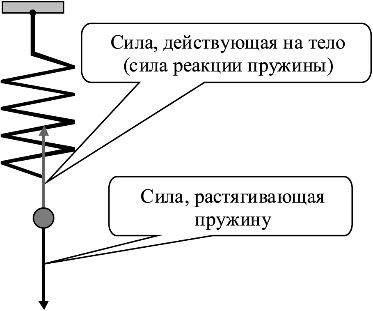 Обращаем особое внимание, что две силы (3.3) всегда приложены к различным телам. Предположение о равенстве сил (3.3) самое простое. Опыт показывает, что третий закон Ньютона всегда выполняется, если временем передачи взаимодействия между телами можно пренебречь. 10. Инерциальная система отсчёта Первый закон Ньютона постулирует, что теоретически существуют такие особые системы отсчета, в которых сохраняется равномерное движение тела, если все силы, действующие на него, уравновешены. Такие системы отсчета называются инерциальными. Нетрудно показать, что если есть хоть одна такая система, то их должно быть бесконечно много. Действительно, все системы отсчета, движущиеся равномерно относительно какой-либо инерциальной системы, тоже являются инерциальными. Это следует из того факта, что в уравнение движения (3.1) входит ускорение материальной точки, а не ее скорость. А ускорение тела не меняется, если к его мгновенной скорости в одной системе отсчета v(t) добавить любую постоянную во времени скорость V: 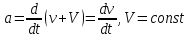 Мы можем пользоваться и такими системами отсчета, в которых тела даже при полностью уравновешенных силах будут двигаться с ускорением. Такие системы называются неинерциальными, и в них не выполняются законы Ньютона. В качестве примера можно назвать систему отсчета, привязанную к неравномерно движущемуся поезду. В такой системе отсчета различные тела будут самопроизвольно (с точки зрения наблюдателя) ускоряться и перемещаться, хотя никаких видимых взаимодействий с окружающими телами не появляется. Таким образом, с точки зрения этого наблюдателя, первый закон Ньютона перестает быть справедливым. Законы Ньютона верны только в инерциальных системах отсчета. Для того чтобы можно было по-прежнему пользоваться этими законами даже в неинерциальных системах, мы вынуждены будем вводить так называемые «псевдосилы инерции». Эти псевдосилы не отвечают никакому взаимодействующему телу (то есть не являются материальными силами), а связаны только и исключительно с тем, что система отсчета наблюдателя движется с ускорением относительно инерциальных систем отсчета. 11. Неинерциальная система отсчёта Неинерциальная система отсчета - произвольная система отсчета, не являющаяся инерциальной. Всякая система отсчета, движущаяся с ускорением относительно инерциальной, является неинерциальной. Наблюдатель, расположенный в неинерциальной системе отсчета, испытывает воздействие так называемых псевдосил инерции, которые нельзя соотнести с каким-либо телом, со стороны которого они бы действовали. В такой системе отсчета законы Ньютона необходимо поправить. Так, если система отсчета K′ (величины, измеренные в этой системе, будем обозначать символами со штрихами) имеет постоянное по величине и направлению ускорение A относительно инерциальных систем отсчета, то во второй закон Ньютона, описывающий движение тела в этой системе отсчета, кроме реальных сил F, необходимо добавить член, описывающий «псевдосилу инерции», который пропорционален массе этого тела. Даже если реальные силы отсутствуют, тела в неинерциальной системе движутся не равномерно, а с ускорением a′=−A: ma′=F−mA. Эти «силы инерции» не только сообщают телам ускорения, но и отклоняют подвесы от вертикального направления, деформируют закрепленные тела и т. п. С точки зрения наблюдателя эти силы вполне осязаемы (их можно измерить), но с физической точки зрения это не настоящие силы, так как нет второго тела – источника силы. Появление «сил инерции» вызвано исключительно неравномерным движением системы отсчета наблюдателя относительно инерциальных систем. Все псевдосилы инерции, вызванные неинерциальностью системы отсчета, обязательно пропорциональны массам тел, на которые они воздействуют. Современные приборы позволяют обнаруживать неинерциальность большинства систем отсчета, используемых в окружающем мире. Инерциальными системами являются лишь те, которые движутся равномерно относительно системы, центр которой связан с самым массивным ближайшим телом – Солнцем, а оси координат неподвижны относительно самых удаленных звезд. Эта система отсчета называется гелиоцентрической. В неинерциальной вращающейся системе отсчета, связанной с Землей, появляются псевдосилы инерции, величина и направление которых довольно сложно зависят от положения наблюдателя, а также величины и ориентации скорости его движения относительно оси вращения Земли. 12. Принцип относительности Галилея Следствием первого закона Ньютона является утверждение: Если наблюдатель находится в инерциальной системе отсчета, то все тела, на которые не действуют силы, будут находиться в покое или двигаться с постоянными скоростями. Всегда можно выбрать систему отсчета так, чтобы, по крайней мере, одно тело, на которое не действуют силы (или действие всех сил уравновешено), в ней покоилось. Состояние покоя и равномерного прямолинейного движения эквивалентны. Опыт показывает, что силы – это векторы, то есть они преобразуются по известному для векторов закону. В частности, при переходе к другой инерциальной системе сохраняется модуль силы. А значит, и вид уравнения движения, в которое входит ускорение, остается неизменным во всех инерциальных системах отсчета. Физически это означает, что все законы механики, а значит, и поведение физических тел, одинаково во всех таких системах. Это утверждение называется принципом относительности, который впервые сформулировал Галилей: никакой механический эксперимент не позволяет обнаружить абсолютное движение инерциальной системы отсчета, то есть нельзя определенно сказать, что какая-то инерциальная система является преимущественной – все инерциальные системы равноправны. Математически принцип Галилея выражается в том, что если координаты r всех взаимодействующих тел одновременно подвергнуть преобразованию r′=r+V⋅t, где V – постоянный произвольный вектор, то все их относительные скорости и ускорения не изменятся. Это вытекает из того, что уравнения движения никак не изменяются при преобразовании координат. 13. Центр инерции (центр масс) протяженного тела Рассмотрим макроскопическую систему взаимодействующих материальных точек. Частным случаем такой системы является протяженное материальное тело. Для каждой материальной точки составной системы можно записать уравнение движения: 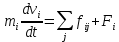 (4.1) (4.1)где fij – вектор силы, действующей на i-ую материальную точку тела со стороны j-ой материальной точки, а Fi – внешняя сила, действующая на i-ую частицу. Поскольку массы всех частиц считаются неизменными, их можно в (4.1) внести под знак производной. Сложим теперь все уравнения (4.1) нашей системы материальных точек. В силу третьего закона Ньютона (fij=−fji) все внутренние силы при суммировании сокращаются, и мы получаем: 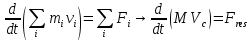 (4.2) (4.2)где M=∑mi – общая масса всей системы, Fres=∑Fi – результирующая сила – векторная сумма всех внешних сил, действующих на систему, а вектор усредненной скорости VC определен выражением: 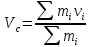 (4.3) (4.3)Здесь проявилось замечательное свойство законов Ньютона – их воспроизводство в больших масштабах. Уравнение (4.3) показывает, что произвольная система материальных точек в целом подчиняется второму закону Ньютона, если в качестве массы брать суммарную массу системы, расположенную в точке, координата которой задается радиус-вектором, вычисляемым по формуле: 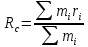 (4.4) (4.4)Точка с координатами (4.4) называется центром инерции системы материальных точек. Система в целом ведет себя как материальная точка с массой M и координатами RC, движущаяся под действием равнодействующей силы Fres. Если система изолированная, то есть на нее не действуют внешние силы, то центр инерции движется равномерно и прямолинейно, то есть по инерции. В соответствии с первым законом Ньютона, всегда можно выбрать систему отсчета так, чтобы система точек как целое покоилась. Эта система отсчета называется системой центра инерции или C-системой. Система отсчета, связанная с наблюдателем, называется лабораторной системой или L-системой. Поэтому поведение частиц внутри системы точек удобно исследовать именно в C-системе, когда исключено ее движение как целого, даже если это движение и неравномерное. 14. Определение положения центра масс у простых тел Для определения положения центра масс у простых по форме тел можно эффективно использовать следующие правила: 1. Если тело состоит из материальных точек, то, выбирая удобную систему координат, можно определить координаты центра масс непосредственно по формуле (4.4). Центр масс системы двух материальных точек расположен между ними и лежит на линии, их соединяющей. Действительно, выбирая ось координат так, чтобы обе точки лежали на ней (см. рис. 4.2), причем одна из точек находится в начале координат, получим с помощью (4.4) координату центра масс xC. Рис. 4.2 − Центр масс системы двух материальных точек 2. Для симметричных тел имеет место теорема: Если тело однородное и симметричное, то его центр масс совпадает с центром симметрии. Рис. 4.3 − Центр масс симметричных тел 3. Если тело можно разбить на части, центр масс которых найти легко, то центр масс всего тела ищем по формуле (4.4), в которую теперь входят координаты и массы отдельных частей. Центр масс произвольного однородного треугольника лежит в точке пересечения медиан. 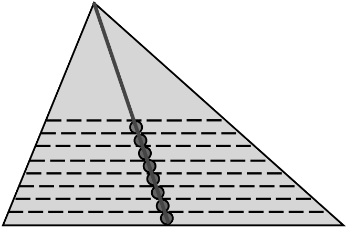 Рис. 4.4 − К определению центра масс треугольника Действительно, треугольник всегда можно разбить на узкие полоски, расположенные параллельно одной из сторон. Центры масс каждой полоски лежат в их серединах, поэтому и центр масс всех полосок лежит на медиане. Проводя аналогичное разбиение на полоски, параллельные другой стороне треугольника, получим другую медиану. Точка пересечения медиан и будет соответствовать центру масс треугольника. 15. Импульс тела Произведение массы материальной точки на ее вектор скорости называется импульсом: p=mv. (4.5) Для сложного тела или системы материальных точек имеем выражение для импульса:  (4.6) (4.6)Импульс тела – это векторная величина, которая сохраняется, если тело изолировано, то есть сумма внешних сил равна нулю. Этот закон сохранения импульса верен при любых изменениях, происходящих внутри системы под действием ее внутренних взаимодействий. Например, если свободно летящий снаряд разорвался на несколько осколков, то центр масс этих осколков будет двигаться так, как будто никакого взрыва не было. Наиболее просто закон сохранения импульса проявляется, если тело под действием каких-либо внутренних причин распадается всего на две части. Тогда из закона с достоверностью следует, что в C-системе импульсы двух частей лежат на одной прямой линии. Именно на этом принципе основано действие реактивного двигателя или явления отдачи при выстреле. В C-системе отсчета полный импульс тела PC всегда равен нулю, даже если движение центра масс неравномерное. Действительно, если мы перейдем в систему отсчета, движущуюся относительно лабораторной системы со скоростью (4.3), то получим с учетом определения (4.6) для суммарного импульса PC:  16. Механическая работа и кинетическая энергия В механике элементарная работа определяется как скалярное произведение вектора силы F и вектора малого перемещения ds: dA=F⋅ds=F ds⋅cosϑ. (4.7) Докажем теперь теорему о кинетической энергии: Работа равнодействующей силы равна изменению кинетической энергии тела. Для этого умножим скалярно обе части уравнения движения Ньютона (3.1) на вектор перемещения и сделаем в левой части элементарные преобразования:  (4.8) (4.8)Отсюда становится ясным физический смысл производства работы как процесса изменения кинетической энергии тела. Если результирующая сила равна нулю, то кинетическая энергия тела остается постоянной. Это свойство роднит кинетическую энергию и импульс тела, который тоже не меняется в отсутствии внешней силы. Такие величины, характеризующие состояние физической системы и сохраняющиеся во времени, называют интегралами движения, так как они появляются после однократного интегрирования уравнений движения. Импульс и кинетическая энергия материальной точки связаны простым уравнением:  (4.9) (4.9)Если проинтегрировать (4.8), то получим интегральное выражение теоремы для работы при перемещении тела из точки 1 в точку 2:  (4.10) (4.10)Работа математически выражается как интеграл проекции силы на направление перемещения вдоль траектории движения. Работа может быть как положительной, так и отрицательной. В последнем случае говорят, что система совершает работу против силы, тогда как при A>0 сила совершает работу над системой. Если сила ортогональна перемещению, то она не совершает никакой работы, и кинетическая энергия тела не меняется. Вполне очевидно, что работа суммы нескольких сил, действующих на частицу одновременно, равна сумме работ, которые бы совершила каждая сила в отдельности. Работа, совершаемая в единицу времени, называется мощностью. Отметим, что работа – это интегральная величина, а мощность – дифференциальная, то есть мощность имеет смысл даже в одной точке траектории:  . (4.11) . (4.11)Единицей работы и энергии является Джоуль, а мощности Ватт. Иногда применяют устаревшую единицу мощности 1 лошадиная сила = 736 Вт. |