Теоретические основы начального курса математики с методикой пре. Занятие 3 Обучающийся Захарян Татьяна Сергеевна Преподаватель Старкова Татьяна Андреевна
 Скачать 377.5 Kb. Скачать 377.5 Kb.
|
|
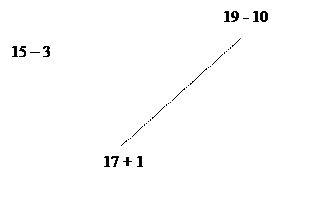
Программа среднего профессионального образования 44.02.05 Коррекционная педагогика в начальном образовании Дисциплина: Теоретические основы начального курса математики с методикой преподавания Практическое занятие №3 Выполнил: Обучающийся Захарян Татьяна Сергеевна Преподаватель: Старкова Татьяна Андреевна Практическое занятие №3Задание 1. Подберите из учебников математики 4 класса для начальной школы (УМК по выбору) различные задания (не менее 10 заданий), в ходе которых учащиеся учатся выполнять различные действия и операции с именованными числами. Ответ: 1. Превратить 2 км в метры. 2. 15 метров превратить в сантиметры. 3. Выразите: в метрах и сантиметрах - 7280см, 32578см, 41283см, 83057см, 65021см. 4. В рублях и копейках – 920коп., 376коп.. 2593коп., 5074коп.. 1000коп. 5. Выразите: А)в метрах – 66км 256м, 9км 59м, 10км 240м, 68км 5м Б)в дециметрах – 34м 10см, 90м 30см, 30м 200мм, 15м 80см, 65дм 800мм В)в сантиметрах – 5м 24см, 2м 9см, 40м 7см, 32м 8см Г)в миллиметрах – 4дм 5см, 1дм 6см, 89см 3мм, 32дм 8см 6.Выразите: А)в тоннах – 100ц, 15000кг, 4000ц, 8000кг, 6700ц Б)в центнерах – 32т 8ц, 4400кг, 8т 200кг, 700000кг, 6200кг В)в килограммах – 19т 78кг, 45т 5ц, 13т 246кг, 10т 720кг, 5ц 4кг Г)в граммах – 45кг, 6кг 778г, 1кг 50г, 80кг, 53кг 2г 7. Выразите: А)в месяцах – 32года, 68лет, 90лет, 56лет, 102года Б)в часах – 52сут, 14сут, 65сут, 70сут, 100сут В)в минутах – 64ч, 315ч, 720ч, 105ч, 280ч Г)в секундах – 206мин, 359мин, 120мин, 723мин, 902мин 8. Выразите: А)в минутах и секундах – 850с, 32ч 80с, 652с, 3ч 2мин 75с, 900с Б)в часах и минутах – 750мин, 3сут 3ч 9мин, 920мин, 7сут 6ч 72мин, 645мин 9. Выразите в более крупных мерах: А)70000 кг, 24653кг, 300258кг, 12006кг, 100200кг Б)6836г, 28904г, 14070г, 40098г,200010г В)265ц, 1318ц, 2054ц, 74020ц, 32001ц Г)3000м, 23568м, 500000м, 98743м, 523000м Д)6000мм, 74800мм, 231000мм, 40200мм 10.Выразите в более мелких единицах: А)20т 72кг, 9кг 6г, 8т 70ц, 63т 26кг, 15ц 19кг, 18т 9ц Б)50м 8дм, 3600мм, 48641м, 20м 7мм, 6800мм, 260015м В)12км, 28км, 6км 357м, 15км 013м, 54км 1м Задание 2. Разработайте конспект урока по теме «Вычисление площадей фигур с помощью палетки». Конспект урока оформите по структуре: 1. Тема: 2. Класс: 3. УМК (авторы, название программы): 4. Цели: 5. Оборудование: 6. Ход урока: Ответ: 1. Тема: Вычисление площадей фигур с помощью палетки 2. Класс: 4 3. УМК (авторы, название программы): М.И.Моро, М.А.Бантова, Г.В.Бельтюкова, С.И.Волкова, С.В.Степанова – М. Просвещение 4. Цели: формировать умение нахождения площади фигур различной формы с помощью палетки 5. Оборудование: Компьютер, проектор, презентация, палетка 6. Ход урока: Для решения многих инженерных задач при строительстве новых домов, фабрик, водохранилищ и т.п. требуется знать площади отводимых под строительство земельных угодий. Эти площади могут быть рассчитаны по результатам измерений на местности или определены по карте. Для этого применяют способ разбивки участка на простые геометрические фигуры или используют прозрачную плёнку с нанесёнными квадратами – палетку. Палетку накладывают сверху на карту и подсчитывают число полных квадратов, расположенных внутри контура участка N1. Затем подсчитывают число квадратов N2, через которые проходит граница участка (см. рисунок). Тогда площадь измеряемого участка вычислится так: S0 · (N1+1/2N2), где S0 – площадь под одним квадратом палетки. Посмотрев масштаб карты, легко вычислить площадь нужного её участка.   Как узнать площади таких фигур? Чем измерить площадь фигур? Какие используют единицы измерения? Палетка - прозрачная плёнка или пластинка, расчерченная на квадраты известных размеров, при помощи которых определяется площадь наложением на фигуру. Алгоритм: Наложить палетку Сосчитать количество полных клеток Сосчитать количество неполных клеток и разделить на 2 Сложить количество полных клеток и половинное количество неполных. Записать полученный результат с единицей измерения 1.Определите, какая фигура имеет большую площадь, а какая - меньшую, и решите ребус соответствия.        INCLUDEPICTURE "https://topuch.ru/zanyatie-3-obuchayushijsya-lukina-oksana-mihajlovna-prepodavat/385025_html_289c42e2f16716ab.jpg" \* MERGEFORMATINET INCLUDEPICTURE "https://topuch.ru/zanyatie-3-obuchayushijsya-lukina-oksana-mihajlovna-prepodavat/385025_html_289c42e2f16716ab.jpg" \* MERGEFORMATINET  Правильный ответ: Прямоугольник – большую, круг – меньшую. 2. Сторона клетки фигуры на рисунке равна 1 см. Найдите её площадь и периметр.  Правильный ответ: Площадь 7 см2; Периметр 12 см 3.Выберите единицу измерения площади: 1)см 2) км 3) кв. См 4. Выберите правильное утверждение о площади: А) это та часть плоскости, которую занимает фигур Б) это сумма длин всех сторон В) это всё, что находится вокруг фигуры Задание 3. Разработайте урок-игру для младших школьников (класс по выбору) для закрепления знаний свойств изученных геометрических фигур. Формат урока не ограничен (урок-путешествие, урок-сказка и т.п.). Тема: Геометрические фигуры Цели: Повторить и закрепить знания об изученных геометрических понятиях (фигурах), их свойствах. Повторять случаи сложения и вычитания в пределах 20,продолжать формировать умение составлять задачи на разностное сравнение и решать их, закреплять умение чертить отрезки. Развивать внимание, логическое мышление, речь, воображение, смекалку. Воспитывать чувство уважения друг к другу, любовь и интерес к предмету. Оборудование: 1. Учебник – тетрадь «Математика», 1 класс, 2 часть, автор Чекин А.Л. 2. Геометрические фигуры в конверте ( индивидуально для каждого ученика). Ход урока I. Орг. момент. Долгожданный дан звонок, Начинается урок! II. Сообщение темы и целей урока Сегодня мы отправимся в путешествие по стране Геометрии, так как тема урока – Геометрические фигуры. Повторим все геометрические фигуры, изученные в 1 классе, будем решать примеры и задачи. А кому мы будем помогать в этом путешествии, вы узнаете из стихотворения: Пуст сегодня дворик наш, За окошком хмуро. Я взял фломастер, карандаш, Решил чертить фигуры. Передо мной бумаги лист, До чего ж он бел и чист. Фломастером ткнешь Посредине листочка И на листе появляется … (точка) Слайд № 2 Но прежде чем отправиться в далекое путешествие, нужно провести разминку. III. Устный счет 1) «Разминка для ума» Работа с числом - Какое сегодня число? (17 мая) Слайд № 3 - Назовите число, которое ему предшествует. - Назовите число, которое следует за ним. - Какое это число: однозначное или двузначное? - Сколько десятков и единиц в числе? - Представьте число в виде суммы разрядных слагаемых. Слайд № 4 - 17 это 9 и сколько? Слайд № 5 Размялись, а теперь - в путь! - Я тетрадочку открою, Уголочком положу….. Запишите число, классная работа. 2) Решение примеров на сложение и вычитание в пределах 20 без перехода через разряд - Точка пошла путешествовать. А какой она прошла путь, мы увидим, если выполним такое задание. Слайд № 6 - Я называю число, а вы находите пример с таким ответом.  - 10 14 + 0 - 10 14 + 0 - 14 17 + 1 - 14 17 + 1- 18 15 – 3
- Остался последний пример. Сосчитайте, назовите ответ. IV. Повторение и закрепление пройденного материала о геометрических понятиях. Беседа о ломаной линии - На какую геометрическую фигуру похож путь нашей точки? (ломаная линия) - Как называются отрезки, составляющие ломаную линию? (звенья) - Посчитайте количество звеньев. - А как называются концы звеньев? (вершины) - Посчитайте количество вершин. - Концы ломаной линии соединены друг с другом? (нет) - Как называется такая ломаная линия? (незамкнутая) 2) Работа с учебником - тетрадью с.72 № 1 Самостоятельная работа «Группировка геометрических фигур» - Ломаная линия привела Точку на геометрическую поляну. - Какие фигуры увидела там Точка? - Приготовьте 3 карандаша: зеленый, коричневый, желтый. Зеленым цветом обведите треугольники, круги – коричневым, а прямоугольники – желтым. Проверка. Слайд № 7 - Сколько треугольников на поляне? - Докажите, почему эту фигуру называют треугольником? - Какие треугольники будут симметричные? - Проведите прямую, относительно которой они симметричны. - Покажите такой треугольник, который имеет прямой угол. - С помощью какого инструмента это доказать? (угольника) - Сколько кругов на поляне? - Являются ли они симметричными фигурами? - Сколько прямоугольников? Почему их так называют? - Есть ли среди прямоугольников такие, у которых все стороны равны? - Найдем среди прямоугольников симметричные. Проведите ось симметрии. - Какие фигуры не встретились на поляне, но мы их изучали в 1 классе? (прямая, кривая, точка, ломаная линия) Физминутка Слайд № 8 Много ль нам, ребята, надо Для умелых наших рук? Нарисуем 2 квадрата, А на них - огромный круг. А потом еще кружочек, Треугольный колпачок, Вот и вышел…. Очень сказочный зверек. V. Решение задачи Слайд № 9 - Ну а теперь поможем Точке составить задачу про геометрические фигуры, чтобы она решалась вычитанием. (На поляне было 6 треугольников и 5 кругов. На сколько треугольников больше, чем кругов?) - Назовите условие задачи. Вопрос задачи. - Как узнать, на сколько одно число меньше или больше другого? - Запишите решение и ответ задачи. - Проверяем. Слайд № 10 -Поехала Точка дальше на велосипеде. Динамическая пауза. Слайд № 11 (Имитация езды на велосипеде. Проведение гимнастики для глаз) VI. Работа с отрезками - Ехала Точка, ехала, а впереди – речка. Поможем перебраться Точке? Построим мост. Но для этого нам нужно выполнить вот такое задание. Слайд № 12 - Начертить один отрезок длиной 6 см, а другой – на 3 см короче первого. Дети выполняют задание в рабочих тетрадях. - Молодцы, справились с заданием. Помогли Точке перебраться через речку. - И увидела Точка вот такую фигуру. Слайд № 13 - На что похожа эта фигура? (на конверт) Работа в парах. Учебник – тетрадь с. 72 № 3 - Посчитайте, сколько здесь отрезков? - Покажите замкнутую ломаную линию на этом чертеже. - Обведите всю фигуру, не отрывая карандаш от бумаги и не проходя по одному и тому же отрезку дважды. VII. Практическая работа Составление геометрической фигуры - Что обнаружила Точка в конверте? - Геометрические фигуры. Слайд №14 - Какие это фигуры? Сколько их? - Соберите из них такую фигуру. Слайд № 15 - На что она похожа? (домик) - Понравился домик Точке. Решила она в нем остаться жить. - На этом закончилось наше путешествие по стране Геометрии. VIII. Итог. Самооценка - С какими геометрическими фигурами мы встретились? - Что повторили, помогая Точке? - А теперь оцените свою работу на уроке. Если у вас хорошее настроение, вам было интересно на уроке, у вас все получалось, то поднимите «солнышко», а если вы чувствовали себя неуютно, у вас что-то не получалось, тогда – «тучку». Слайд № 16 - Точка благодарит вас за помощь, которую вы ей сегодня оказали, и вручает за хорошую работу призы. Задание 4. Изучив методическую литературу, составьте классификацию простых задач, с решением которых знакомятся учащиеся начальной школы. В методическом отношении удобна следующая классификация простых задач: деление задач на группы в зависимости от тех понятий, которые формируются при их решении. С этой точки зрения выделяют три группы задач. 1-я группа - простые задачи на усвоение конкретного смысла арифметических действий. В эту группу входят такие задачи: 1) Нахождение суммы двух чисел. Маляр покрасил в одной квартире 6 дверей, а в другой 4. Сколько дверей покрасил маляр? 2) Нахождение остатка. Школьники сделали 6 кормушек. 2 кормушки они повесили в школьном саду. Сколько кормушек им осталось повесить? 3) Нахождение суммы одинаковых слагаемых (произведения). Школьники посадили в парке 4 ряда березок по 5 штук в ряду. Сколько березок они посадили? 4) Деление на равные части. В 3 палатках жили 24 туриста, в каждой палатке поровну. Сколько туристов жили в каждой палатке? 5) Деление по содержанию. Каждая бригада школьников окопала по 8 яблонь, а всего школьники окопали 24 яблони. Сколько всего бригад школьников выполняли эту работу? 2-я группа - простые задачи на усвоение связи между компонентами и результатами арифметических действий. В эту группу входят такие задачи: 1) Нахождение первого слагаемого по известным сумме и второму слагаемому. У кормушки было несколько снегирей, к ним прилетели 6 синиц. И их стало всего 9. Сколько снегирей было у кормушки? 2) Нахождение второго слагаемого по известным сумме и первому слагаемому. У кормушки было 3 снегиря, к ним прилетели несколько синиц и их стало 9. Сколько синиц прилетело? 3) Нахождение уменьшаемого по известным вычитаемому и разности. Школьники сделали несколько скворечников. Когда 2 скворечника они повесили на дерево, то у них осталось 4 скворечника. Сколько скворечников сделали школьники? 4) Нахождение вычитаемого по известному уменьшаемому и разности. Школьники сделали 6 скворечников. Когда несколько скворечников они повесили на дерево, то у них осталось еще 4 скворечника. Сколько скворечников повесили школьники? 5) Нахождение первого множителя по известным произведению и второму множителю. Неизвестное число умножили на 8 и получили 32. Найти неизвестное число. 6) Нахождение второго множителя по известным произведению и первому множителю. 9 умножили на неизвестное число и получили 27. Найти неизвестное число. 7) Нахождение делимого по известным делителю и частному. Неизвестное число разделили на 9 и получили 4. Найти неизвестное число. 8) Нахождение делителя по известным делимому и частному. 24 разделили на неизвестное и получили 6. Найти неизвестное число. 3-я группа - простые задачи, раскрывающие новый смысл арифметических действий: понятия разности и кратного отношения. В эту группу входят такие задачи, связанные с понятием разности: 1) Разностное сравнение чисел или нахождение разности двух чисел (1 вид). У Миши было 8 шариков, а у Коли 5 шариков. На сколько у Миши шариков больше, чем у Коли? 2) Разностное сравнение чисел или нахождение разности двух чисел (2 вид). У Тани 10 книг, а у Оли 8 книг. На сколько книг у Оли меньше? 3) Увеличение числа на несколько единиц (прямая форма). На первой тарелке было 7 груш, а на второй на 3 груши больше. Сколько груш на второй тарелке? 4) Увеличение числа на несколько единиц (косвенная форма). У Миши 4 фломастера, это на 8 фломастеров меньше, чем у Тани. Сколько фломастеров у Тани? 5) Уменьшение числа на несколько единиц (прямая форма). Школьники собрали с первой грядки 23 кг моркови, со второй на 3 кг меньше. Сколько килограммов моркови собрали со второй грядки? 6) Уменьшение числа на несколько единиц (косвенная форма). В колхозе было 12 тракторов, это на 4 больше, чем комбайнов. Сколько комбайнов было в колхозе? В эту группу также входят простые задачи, связанные с понятием кратного отношения. 1) Кратное сравнение чисел или нахождение отношения двух чисел (1вид). На проводе 6 ласточек и 2 воробья. Во сколько раз ласточек больше, чем воробьев? 2) Кратное сравнение чисел или нахождение отношения двух чисел (2 вид). В столовой израсходовали 8 кг муки и 24 кг крупы. Во сколько раз меньше израсходовали муки, чем крупы? 3) Увеличение числа в несколько раз (прямая форма). В одном куске 6 м проволоки, а в другом в 2 раза больше. Сколько метров проволоки во втором куске? 4) Увеличение числа в несколько раз (косвенная форма). У брата было 6 простых открыток, их было в 2 раза меньше, чем цветных открыток. Сколько цветных открыток было у брата? 5) Уменьшение числа в несколько раз (прямая форма). В пруду плавали 9 гусей, а уток в 3 раза меньше. Сколько уток плавало в пруду? 6) Уменьшение числа в несколько раз (косвенная форма). Длина первой доски 18 дм, это в 3 раза больше длины второй доски. Какова длина второй доски? Простые задачи на сложение и вычитание изучаются в 1 классе в связи с изучением соответствующих действий, а задачи на умножение и деление - во 2 классе. Задание 5. Выберите из учебника математики 1 класса задания (не менее 6 заданий), подготавливающие младших школьников к введению понятия «арифметическая задача». Разработайте два задания. А) С дерева упало 5 яблок , затем еще 3. Покажи, сколько яблок упало с дерева. Б) Юля съела утром 3 яблока, вечером еще 7. Покажи, сколько всего яблок съела Маша. В) У Коли было 4 куска пирога, у Пети — на два куска больше. Покажи, сколько кусков пирога у Пети. Г) С одного дерева упало 5 яблок, с другого на 3 больше. Покажи, сколько упало со второго дерева. Д) У Коли было 4 куска пирога, у Пети — 2. Покажи, сколько кусков пирогов было у них вместе. Е) В гараже стояли грузовые и легковые машины. После того как З грузовые машины уехали, осталось 4 легковых. Покажи, сколько всего машин стояло в гараже. Задание 6. Прочитайте задачу: «В школьную столовую привезли 6 кг лимонов, яблок на 24 кг больше, чем лимонов, а груш на 12 кг меньше, чем яблок. Сколько килограммов груш привезли в школьную столовую?» Вопросы: Каким способом (синтетическим, аналитическим или аналитико-синтетическим) лучше проводить разбор этой задачи? Покажите методику работы над арифметической задачей на примере данной задачи (этапы работы над задачей смотрите в лекции). Аналитико-синтаксическим Лимоны-6кг Яблоки-?,на 24кг> Груши-?,на 12кг< У вопроса про груши мы обводим главный вопрос в кружок. От яблок к лимонам проводим квадратную стрелку. От груш к яблокам проводим квадратную стрелку. 1)24+6=30(кг)-яблоки. 2)30-12=18(кг) Ответ:18 кг груш привезли в школьную столовую. Задание 7. Разработайте контрольно-измерительные материалы для диагностики результатов обучения младших школьников по теме «Дроби». Вид контрольно-измерительных материалов по выбору. В работе должно быть не менее 10 заданий. 1.Укажи дробь: А) 6 Б) 006 В) 2. В дроби над чертой пишется: А) числитель Б) делитель В) знаменатель Г) множитель 3. В дроби под чертой пишется: А) множитель Б) знаменатель В) числитель Г) делитель 4. Укажи наименьшую дробь: А) 5. Укажи наибольшую дробь: А) 6. При сложении А) 7. При вычитании А) 8. А) 60 Б) 4 В)36 Г) 40 9. Укажи целое, если А) 1 Б) 17 В) 18 Г) 72 10. А) 10минут Б) 12 минут В) 15 минут Г) 30 минут 11. А) 1 дм Б) 1 см В) 1 мм Г) 10 дм 12. Чтобы найти А) 56 х 4 : 3 Б) 56 : 4 - 3 В) 56 : 4 +3 Г) 56 : 4 х 3 13. Чтобы найти число, А) 42 х2 : 3 Б) 42 : 3 + 2 В) 42 : 2 х 3 Г) 42 – 2 + 3 Задание 8. Изучите конспект урока. Урок математики в 4 классе по теме «Доли и дроби». Цель урока: дать общее представление о долях, научить учащихся называть, записывать и сравнивать доли Задачи урока: - обучающие – ввести новое понятие «доля числа», учить определять долю числа, записывать дроби, познакомить с терминами «доля», «дробь», «числитель», «знаменатель»; - развивающие – развивать логическое мышление, математическую речь, навыки устного счета, внимание, память, мышление; - воспитывающие – воспитывать коллективизм, аккуратность. Ход урока 1. Знакомство с темой урока. – Людям часто приходится делить целое на доли. А помните известный мультик «Апельсин» Посмотрим, как животные делили апельсин. Смотрите внимательно, после просмотра я задам вам вопросы. - Как в песенке, животные называют равные части? (Дольки). – Кто из вас был внимательным? Сколько долек было в апельсине? (Пять долек). – Сколько долек поучил каждый? (Одну дольку апельсина). - Как вы думаете, апельсин был разделён на равные части? (Да). - Как по-другому, можно назвать эти равные части? (Доли). 2. Постановка учебных задач. - Как на языке математики назвать и записать, какую долю (часть) апельсина получил каждый из животных? ( Не знаем) - Что, на ваш взгляд, нам следует узнать, чему научиться? (Научиться записывать, называть и сравнивать доли). - В результате совместных рассуждений, мы определили цель урока. (Научиться записывать, называть и сравнивать доли). 3. Работа над формированием понятий «Доли» и «Дроби». - Давайте, определим, что же называют долями? Для этого еще раз вспомним, как животные делили апельсин - Сколько частей досталось каждому животному? ( По одной части). - Что можно сказать про каждую из частей? Какие это части? (Равные). - Значит, каждому досталось по одной равной части от целого апельсина. - Сделайте вывод, что такое доля. (Доля – это одна или несколько равных частей целого.) (На доске появляется запись: 1 часть из 5). В математике пишут короче: 1/5. Для записи понадобится 2 клеточки, между ними проводим черту. Число под чертой показывает, на сколько равных частей мы разделили предмет, а над чертой – сколько таких частей взяли. Читаем запись, запишите. - Когда мы «делим» натуральные числа, то используем знак (:). - Но в математике есть еще один знак деления, он называется, «дробная черта» - соответственно числа, записанные с этим знаком, называются дробными. - Кто догадался, как называется данная запись? (Дробь). - Верхняя часть дроби называется числителем, а нижняя – знаменателем. - Что обозначает знаменатель в записи дроби? (На сколько частей разделили предмет). - Что обозначает числитель? (Сколько частей взяли). 4. Отработка умения находить часть от целого и обозначать её дробью. Сравнение дробей. Вопросы: Разработайте задания для 4 этапа урока (работа с количеством заданий – не менее 6 заданий). Какие вопросы можно предложить учащимся на этапе рефлексии? Задания для 4 этапа урока: 1. В столовой испекли 120 пирожков. Продали ¼ всех пирожков. Сколько пирожков осталось? 2. Таня съела ½ конфет из коробки. Это 15 конфет. Сколько конфет было в коробке? 3. В стае было 10 молодых птенцов. Это ¼ от всех птиц в стае. Сколько птиц в стае? 4.Запиши в порядке А) возрастания: Б) убывания: 5.Сравни: 6. Реши задачи: А) Отрезок ткани размером 125 метров разрезали на 5 равных частей. Сколько метров составляет 1 часть? Б) Длина туристского маршрута 350 км. В первый день туристы проехали В) Покупая рыбок в зоомагазине, Коля потратил Возможные вопросы на этапе рефлексии данного урока: – Какая тема урока была? - Какие задачи мы перед собой ставили? – Что такое доля? – Как называется число, которое пишем над чертой? – Что показывает числитель? – Как называется число, которое под чертой? – Что показывает знаменатель? – А ещё мы учились сравнивать доли. Какой вывод сделали? Задание 9. Разработайте дифференцированные задания для самостоятельной работы (высокого, среднего, низкого уровня сложности) для учащихся начальной школы по проверке умений и навыков решать уравнения различного вида (не менее 5 заданий по 3 уровня сложности в каждом задании). 1.Даны выражения: 81 - 29 + 27 400 + 200 + 300 - 100 72 : 9 - 3 400 + 200 + 30 - 100 8:6-7:8 27:3 - 2:6 • 9 84-9-8 54 + 6 • 3 - 72 : 8 Задание для 1-й группы. Вспомните правила о порядке выполнения действий в выражениях и выполните вычисления. Задание для 2-й группы. Разбейте выражения на три группы. Найдите значения выражений. Задание для 3-й группы. Выполните задание для 2-й группы. Подумайте, по какому признаку можно разбить выражения на две группы. 2.Дана задача: «В вазе лежало 5 желтых яблок и 2 зеленых яблока. 3 яблока съели. Сколько яблок осталось?» Задание для 1-й группы. Решите задачу. Подумайте, можно ли ее решить другим способом. Задание для 2-й группы. Решите задачу двумя способами. Задание для 3-й группы. Измените задачу так, чтобы ее можно было решить тремя способами. Решите полученную задачу тремя способами. Задача 3. Задание для 1-й группы. Решите задачу: «Для новогодних подарков привезли 48 кг конфет. В пакетах было 12 кг конфет, в коробках в 3 раза меньше, чем в пакетах, а остальные конфеты были в ящиках. Сколько конфет было в ящиках?» Задание для 2-й группы. Найдите в задаче лишние данные: «Для новогодних подарков привезли 48 кг конфет в двух коробках, трех пакетах и восьми ящиках. В пакетах было 12 кг конфет, в коробках в 3 раза меньше, чем в пакетах, а остальные конфеты были в ящиках. Сколько конфет было в ящиках?» Измените условие и решите задачу. Задание для 3-й группы. Измените вопрос и условие задачи (см. задание для 2-й группы) так, чтобы общее количество конфет стало лишним данным. Запишите новую задачу и решите ее. Задача 4. Метр шелка стоит 20 р., а метр ситца -5 р. На платье нужно 3 м шелка или 2 м 50 см ситца. Сколько шелка и ситца нужно на 1 платье? 1 уровень. Реши задачу по действиям. 2 уровень. Запиши решение задачи выражением. 3 уровень. Из какой ткани платье будет дороже и на сколько? Задача 5. Поезд прошел без остановок 420 км со скоростью 70 км/ч, после остановки на 14 минут прошел еще 300 км со скоростью 75 км/ч. Какое расстояние он преодолел? 1 уровень Реши задачу по действиям. Какая величина в условии лишняя? 2 уровень Запиши решение задачи выражением. 3 уровень Какое расстояние прошел поезд обратно? Задание 10. Составьте систему упражнений для формирования понятия «выражение» и изучения порядка действий в числовых выражениях (не менее 6 упражнений). 1. Полная коробка с яблоками весит 34 кг, а коробка заполненная наполовину, весит 18 кг. Сколько весит пустая коробка? 2. Сколько нужно пятирублёвок, чтобы купить конфету за 25 рублей? 3. Поставьте вместо звездочек знаки арифметических действий так, чтобы равенства были верными: 12*6*2=4 12*6*2=70 12*6*2=24 12*6*2=9 12*6*2=0 4. Расставьте скобки так, чтобы равенства были верными: 25–17:4=2 3•6–4=6 24:8–2=4 5. Поставьте вместо звездочек знаки "+" или "-" так, чтобы получились верные равенства: 38*3*7=34 38*3*7=28 38*3*7=42 38*3*7=48 6. Продолжить запись так, чтобы знак "=" сохранился: 56– (20+1)=56–20... (10+5) • 4=10•4... 60:(2•10)=60:10... | ||||||||||||||||||||||||||||||||||||||||||||||||||