Практическое занятие 3. Практическое занятие №3. Занятие 3. Расчет и построение графика движения поршня
 Скачать 219.1 Kb. Скачать 219.1 Kb.
|
|
Практическое занятие №3. Расчет и построение графика движения поршня Цель: производить расчеты требуемых физических величин в соответствии с законами и уравнениями термодинамики и теплопередачи;; готовить скважину к эксплуатации; овладеть профессиональными (ПК) и общими (ОК) компетенциями: ПК 1.1. Выполнять основные технологические расчеты по выбору наземного и скважинного оборудования. ПК 1.2. Производить техническое обслуживание нефтегазопромыслового оборудования. ОК5. Использовать информационно-коммуникационные технологиив профессиональной деятельности Задание: Произвести расчет и построение графика движения поршня. Ход работы: Произвести расчет движения поршня. Построить график движения поршня. Сделать вывод по работе. Ответить на контрольные вопросы. Оснащение: методические указания по выполнению ПЗ, справочные таблицы, калькулятор, тетрадь, ручка. Литература: Никишенко С.Л. Нефтегазопромысловое оборудование Учебное пособие для средних специальных учебных заведений.- Волгоград: Ин-Фолио, 2008.- 416с., с.16-30 Исходные данные для расчетов приведены в таблице 1.1. Таблица 1.1 - Исходные данные
Коэффициент подачи насоса η0 = 0,8; полный КПД насоса ηн = 0,75. Общие сведения. Согласно теории кривошипно-шатунных механизмов следует, что изменение мгновенной скорости движения поршня во времени с достаточной степенью приближения следует синусоидальному
Следовательно, скорость движения поршня – величина переменная, изменяется по синусоиде (рис. 1.1, б); в мертвых положениях при α = 00 и α = 1800 скорость поршня равна нулю (Sin α = 0), т.к. он останавливается, чтобы изменить направление движения. Максимальное значение скорость поршня приобретет при α = 900 и 2700, то есть при среднем положении поршня (Sin α = 1). Ускорение поршня является первой производной от скорости по времени и определяется по формуле u = r·ω2·Cosα, м/с2 (1.2) Из формулы следует, что ускорение поршня изменяется по косинусоиде (рис. 1.1, в) и в противоположность скорости в мертвых положениях поршня (при α = 00 и α = 1800) будет иметь максимальное значение, причем во второй половине хода со знаком минус. Нулевое значение ускорение будет иметь при α = 900 и α = 2700.  Рисунок 1.1 - Графики скорости и ускорения движения поршня Порядок расчетов. Определить скорость поршня по формуле 1.1. Для построения графика выбрать интервал угла поворота кривошипа 300 и рассчитать соответствующее каждому углу значение скорости. Данные занести в таблицу 1.2. Таблица 1.2 - Скорость движения поршня
Построить график скорости в осях v-α. Скорость отложить по оси ординат, угол поворота – по оси абсцисс (рис. 1.1, а). Определить ускорение поршня по формуле 1.2. Аналогично п.1 заполнить таблицу 1.3 и построить график ускорения (рис. 1.1, б). Таблица 1.3 - Ускорение движения поршня
3.Сделать вывод. Пример. Исходные данные: Число поршней i=3; число рабочих камер z=3; число двойных ходов поршня n=IЗ5мин-1; длина хода поршня S=0,25м; диаметр цилиндра D=18м; давление нагнетания рн=8,5МПа; диаметр штока d=0,06м; коэффициент подачи ηо = 0,8; полный КПД насоса ηн=0,75. Определяем угловую скорость вращения кривошипа и радиус кривошипа r Для построения графика выбираем интервал угла поворота кривошипа 300 и рассчитываем соответствующее каждому углу значение скорости (формула 1.1). Данные заносим в таблицу 1.4. v1 = 0,125 · 14,13 Sin 0 = 0 м/с, Таблица 1.4 - Расчетные данные скорости
Строим график скорости в осях v-α. Скорость откладываем по оси ординат, угол поворота – по оси абсцисс (рис. 1.2). Определяем ускорение поршня (формула 1.2). Аналогично п.1 заполняем таблицу 1.5 и строим график ускорения (рис. 1.3). u1 = 0,125 · 14,132 Cos 00 = 24,96 м/с2,  Угол поворота кривошипа, ° Рисунок 1.2 - Расчетный график скорости движения поршня Таблица 1.5 - Расчетные данные ускорения движения поршня
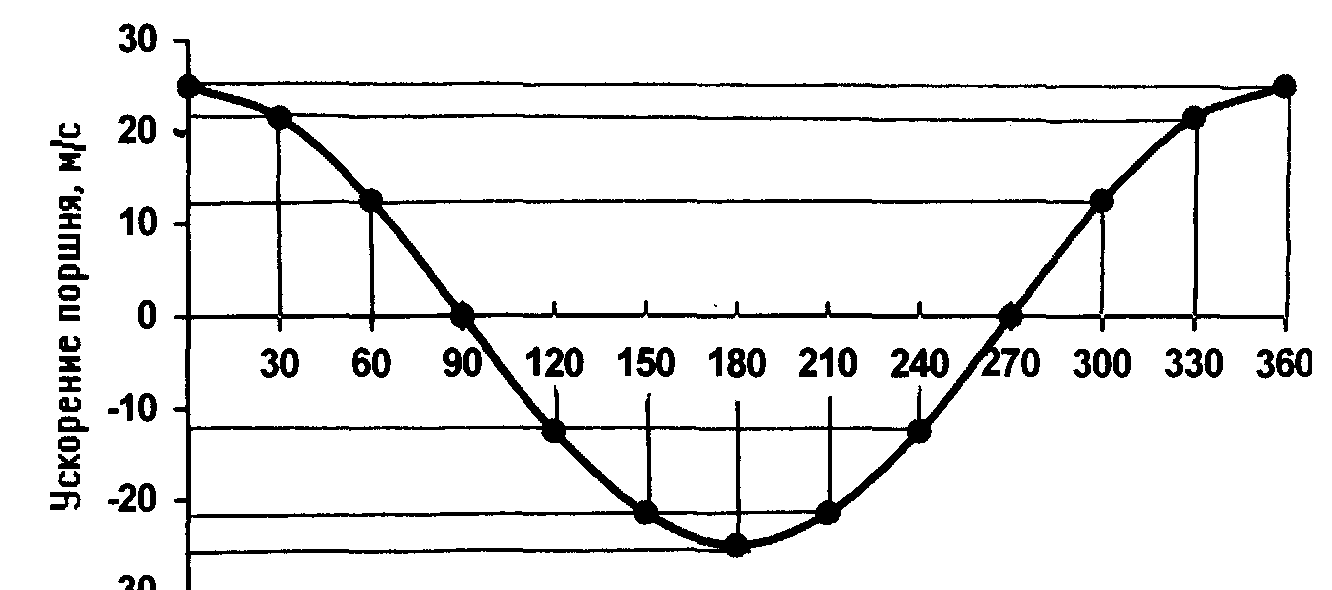 Угол поворота кривошипа, ° Рисунок 1.3 - Расчетный график ускорения движения поршня Вывод: скорость поршня является величиной непостоянной и изменяется по закону синуса. Ускорение является первой производной от скорости по времени и изменяется по закону косинуса. Контрольные вопросы: По какому закону изменяется скорость и ускорение поршня? Почему в «мертвых» положениях скорость поршня равна нулю? Как определить графически и аналитически максимальное ускорение, и максимальную скорость поршня? Каким углам поворота кривошипа соответствует нулевая скорость и нулевое ускорение? Почему подача поршневого насоса является величиной неравномерной? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 -0,88
-0,88