Лекция 31. Занятие №6. Занятие 6 ( Лисичкин В. Т., Соловейчик И. Л. Математика) Раздел Линейная алгебра Тема Матрицы, определители Определители высокого порядка Пример Вычислить определитель 4го порядка

• Название: Занятие 6 ( Лисичкин В. Т., Соловейчик И. Л. Математика) Раздел Линейная алгебра Тема Матрицы, определители Определители высокого порядка Пример Вычислить определитель 4го порядка
• Анкор: Лекция 31
• Дата: 15.09.2022
• Размер: 180 Kb.
• Имя файла: Занятие №6.doc
• Тип: Занятие; #679014

Занятие №6 (Лисичкин В.Т., Соловейчик И.Л. Математика)

Раздел 1. Линейная алгебра

Тема 1.1. Матрицы, определители

Определители высокого порядка..

Пример 1. Вычислить определитель 4-го порядка: .

Решение. Самое большое количество нулей в любой из строк или столбцов равно 2. Поэтому для вычисления определителя выбираем любую строку или столбец с двумя нулями. Выберем, например, первый столбец (при этом говорят, что определитель будет разлагаться по первому столбцу):

.

Появившиеся два определителя 3-го порядка можно считать по приведенной выше упрощенной схеме.

Если среди элементов матрицы нулей мало (или нет вовсе), то можно специальными действиями привести определитель к такому виду, у которого есть строка (или столбец), в которой отличен от нуля только один элемент. После этого определитель легко вычисляется разложением по этой строке (столбцу). Привести определитель к такому виду помогают свойства определителей, рассмотренные ниже.

Свойства определителей

1. Если у определителя какая-либо строка (столбец) состоит из нулей, то определитель равен нулю.

2. Если какие-либо две строки (два столбца) определителя равны или пропорциональны (т.е. элементы одной строки (столбца) получаются умножением элементов другой строки (столбца) на одно и то же число), то определитель равен нулю.

3. Если две строки (два столбца) поменять местами, то определитель изменит знак.

4. Общий множитель элементов любой строки или столбца можно выносить за знак определителя.

5. Если к элементам одной строки (столбца) прибавить соответствующие элементы другой строки (столбца), предварительно умноженные на одно и то же число, то определитель не изменится.

6. Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.

Как сказано выше, с помощью этих свойств можно привести определитель к такому виду, у которого есть строка (или столбец), в которой отличен от нуля только один элемент. Для приведения определителя к такому виду необходимо:

1. 
   Вынести общие множители (если таковые имеются) из строк или столбцов за знак определителя (свойство 4.) . Это позволяет уменьшить элементы определителя (что облегчает его дальнейшее вычисление), а также, возможно, получить элементы, равные 1 или (−1), что поможет выполнению следующего пункта.
   
2. 
   Выбрать строку (или столбец), в которой есть элемент 1 или (−1) (если такие строки или столбцы есть) и с помощью этого элемента (и последнего свойства определителей) обнулять остальные элементы выбранной строки или столбца.
   

Иллюстрирует сказанное следующий пример

Пример 2. = {вынесем 2 из второй строки (свойство 4)} =
2∙ = {С помощью элемента а₂₂=1 и свойства 5 обнуляем все элементы второй строки, кроме самого а₂₂=1. Для этого а) прибавляем к 1-му столбцу 2-ой, умноженный поэлементно на (−5); б) прибавляем к 3-му столбцу 2-ой, умноженный на (−1); в) прибавляем к 4-му столбцу 2-ой, умноженный на (−3)} = 2∙ = {раскладываем определитель по второй строке} =2∙1∙(−1)²⁺² ∙ = {для облегчения вычисления определителя 3-го порядка выносим (−1) из первых двух столбцов, а из третьего (−2) }= −4∙ = {вычисляем определитель третьего порядка по упрощенной схеме}=440
Пример №3.  Вычислить определитель 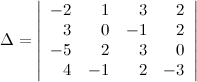  приведением его к треугольному виду.

Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент   будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:



Далее получим нули в первом столбце, кроме элемента 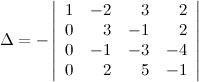  , для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:



Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если диагональный элемент будет равен   , то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя):



Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом: к третьей строке прибавляем три вторых, а к четвертой - две вторых строки, получаем:



Д 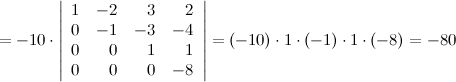алее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:

Ответ. 

Пример 4. Вычислить определитель

Решение:

det A =	3	2	1	-1	=
	1	2	3	6
	-2	-3	1	4
	4	-2	3	-5

К элементам строки 4 прибавляем соответствующие элементы строки 2.

=	3	2	1	-1	=
	1	2	3	6
	-2	-3	1	4
	5	0	6	1

Из элементов столбца 1 вычитаем соответствующие элементы столбца 4, умноженные на 5.

=	8	2	1	-1	=
	-29	2	3	6
	-22	-3	1	4
	0	0	6	1

Из элементов столбца 3 вычитаем соответствующие элементы столбца 4, умноженные на 6.

=	8	2	7	-1	=
	-29	2	-33	6
	-22	-3	-23	4
	0	0	0	1

Разлагаем определитель по элементам четвертой строки. (Подробнее)

= ( - 1 ) 4 + 4 * 1 * 8 2 7 = -29 2 -33 -22 -3 -23

= 8 2 7 = -29 2 -33 -22 -3 -23

Из элементов столбца 3 вычитаем соответствующие элементы столбца 1.

=	8	2	-1	=
	-29	2	-4
	-22	-3	-1

Из элементов столбца 1 вычитаем соответствующие элементы столбца 2, умноженные на 4.

=	0	2	-1	=
	-37	2	-4
	-10	-3	-1

К элементам столбца 2 прибавляем соответствующие элементы столбца 3, умноженные на 2.

=	0	0	-1	=
	-37	-6	-4
	-10	-5	-1

Разлагаем определитель по элементам первой строки.

= ( - 1 ) 1 + 3 * ( -1) * -37 -6 = -10 -5

= - -37 -6 = -10 -5

= - ( -37 * ( -5) - ( -6) * ( -10) ) = - ( 185 - 60 ) = -125

Пример 5. Вычислить определитель .

Решение. Вычислим этот определитель разложением по первому столбцу, но сначала с помощью свойств определителя сделаем нули в этом столбце везде кроме элемента, равного минус единице.

Для этого элементы второй строки умножим на два и прибавим к соответствующим элементам первой строки; элементы второй строки прибавим к соответствующим элементам третьей строки; элементы второй строки умножим на два и прибавим к соответствующим элементам четвертой строки. Эти действия записываем так:

.

Разложив определитель 4-го порядка по 1-му столбцу, свели его вычисление к нахождению одного определителя 3-го порядка, который можно вычислить по правилу диагоналей, разобранному выше. Можно дальше применить свойства определителя и свести этот определитель к одному определителю 2-го порядка. Продолжаем делать нули теперь уже во второй строке, умножая элементы третьего столбца на 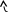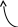и прибавляя к первому и второму столбцам:

=

(-4)

(-4)

Ответ:

Пример 6.

Решить уравнение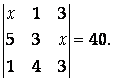



Указание

Разложив определитель, стоящий в левой части равенства, по первой строке, и приравняв его 40, вы получите квадратное уравнение для Х.

Решение

Разложим определитель, стоящий в левой части равенства, по первой строке. Предварительно найдем соответствующие алгебраические дополнения:



Тогда



И требуется решить квадратное уравнение

.

Ответ: 

Домашнее задание

1. 
   Л3, стр. 105-108, №11 (Пехлецкий И.Д.)
   
2. 
   Л4, стр. 71-81, № 56 (Лисичкин В.Т., Соловейчик И.Л.)
   

№11. Решите уравнение




.

№56. Вычислить определитель

Решение домашнего задания

№11.
.

(x+3)(4x-4-3x)+4(3x-4x+4)=0.

(x+3)(x-4)+4(-x+4)=0.

(x-4)(x-1)=0.

Ответ: x₁= 4,x₂= 1.

№56 Вычислить определитель

180