практика. 2 Практическая часть. 1000 у е. 17 месяцев 1,5% в месяц
 Скачать 153.88 Kb. Скачать 153.88 Kb.
|
|
2 Практическая часть 2.1 Расчет схем погашения кредита Исходные данные: 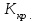 = 1000 у.е.; = 1000 у.е.; = 17 месяцев; = 17 месяцев;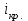 = 1,5% в месяц. = 1,5% в месяц.Схема 1. Схема с равным погашением основного долга и неравной выплатой процентов. В соответствие с данной схемой основной долг погашается равными частями в конце каждого периода времени 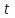 : :
ДМt = 1000 / 17 = 58,82 у.е. Проценты начисляются на долг, имеющийся в начале каждого периода времени 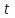 , и выплачиваются в конце каждого периода времени , и выплачиваются в конце каждого периода времени 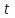 . Накопленная величина срочной уплаты на конец . Накопленная величина срочной уплаты на конец  определяется по формуле: определяется по формуле:
Потоки платежей по погашению основного долга и процентов по кредиту по схеме 1 отразим в таблице 2.1.1. Таблица 2.1.1 Потоки платежей по кредиту по схеме 1
Проверка: 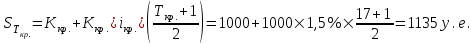 Схема 2. Схема с равным погашением основного долга и равной выплатой процентов. По данной схеме основной долг погашается равными частями в конце каждого периода времени 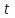 . .Для определения величины уплаты процентов по кредиту в каждый период времени 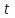 сначала рассчитаем общую величину процентов, подлежащих уплате в течение сначала рассчитаем общую величину процентов, подлежащих уплате в течение  ( (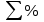 ): ):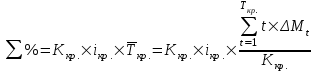 ∑% = 1000*1,5%*((1*58,82+2*58,82+3*58,82+4*58,82+5*58,82+6*58,82+7* *58,82+8*58,82+9*58,82+10*58,82+11*58,82+12*58,82+13*58,82+14*58,82+15*58,82+16*58,82+17*58,82) / 1000) = 1000 * 1,5% * 9 месяцев = 135 у.е. После того, как была рассчитана общая величина процентов, подлежащих уплате ( 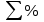 ), определяется размер ), определяется размер  : :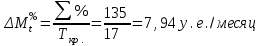 . .Потоки платежей по погашению основного долга и процентов по кредиту по схеме 2 отразим в таблице 2.1.2. Таблица 2.1.2 Потоки платежей по кредиту по схеме 2
Проверка: 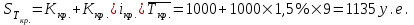 Схема 3. Схема простых процентов. Данная схема предполагает начисление процентов по кредиту каждый период времени 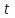 и их выплату в конце каждого периода. Основной долг в размере и их выплату в конце каждого периода. Основной долг в размере 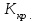 погашается только в конце погашается только в конце  . Накопленную величину срочной уплаты на конец . Накопленную величину срочной уплаты на конец  определим по формуле: определим по формуле: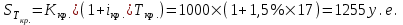 Потоки платежей по погашению основного долга и процентов по кредиту по схеме 3 отразим в таблице 2.1.3. Таблица 2.1.3 Потоки платежей по кредиту по схеме 3
Схема 4. Схема сложных процентов. В соответствии с данной схемой проценты по кредиту начисляются каждый период времени 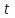 , но не выплачиваются, а добавляются к основному долгу. Основной долг и накопленная величина процентов выплачиваются в конце , но не выплачиваются, а добавляются к основному долгу. Основной долг и накопленная величина процентов выплачиваются в конце  . Накопленная величина срочной уплаты на конец . Накопленная величина срочной уплаты на конец  определяется по формуле: определяется по формуле: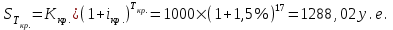 Потоки платежей по погашению основного долга и процентов по кредиту по схеме 4 отразим в таблице 2.1.4. Таблица 2.1.4 Потоки платежей по кредиту по схеме 4
Схема 5. Аннуитетная схема. По данной схеме основной долг и проценты погашаются равными срочными выплатами, то есть 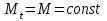 . Определим величину равной срочной выплаты ( . Определим величину равной срочной выплаты (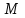 ), которая расписывается на составляющие ( ), которая расписывается на составляющие (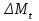 и и  ): ): Потоки платежей по погашению основного долга и процентов по кредиту по схеме 5 отразим в таблице 2.1.5. Таблица 2.1.5 Потоки платежей по кредиту по схеме 5
После проведения расчета схем погашения кредита необходимо выбрать оптимальную схему для кредитора и схему для заемщика. Выбор схемы погашения кредита для кредитора и для заемщика. Для выбора оптимальной схемы погашения кредита построим таблицу 2.1.6. Таблица 2.1.6 Срочные выплаты по схемам погашения кредита
Для кредитора наиболее предпочтительной будет являться схема, которая обеспечивает максимум накопленной величины срочных уплат, то есть:
где 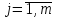 - номера схем погашения кредита; - номера схем погашения кредита;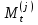 - сумма срочной уплаты в период t по схеме j. - сумма срочной уплаты в период t по схеме j.Для заемщика наиболее предпочтительной будет являться схема, которая обеспечивает минимум накопленной величины срочных уплат, то есть:
где 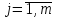 - номера схем погашения кредита; - номера схем погашения кредита;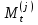 - сумма срочной уплаты в период t по схеме j. - сумма срочной уплаты в период t по схеме j.Отсюда: 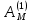 = 73,82/(1+1,5%)1 + 72,94/(1+1,5%)2 + 72,06/(1+1,5%)3+ 71,17/(1+1,5%)4+ 70,29/(1+1,5%)5 + 69,41/(1+1,5%)6+ 68,53/(1+1,5%)7+ 67,64/(1+1,5%)8+ 66,76/(1+1,5%)9+ 65,88/(1+1,5%)10+ 65,00/(1+1,5%)11+ 64,11/(1+1,5%)12+ 63,23/(1+1,5%)13+ 62,35/(1+1,5%)14+ 61,47/(1+1,5%)15+ 60,58/(1+1,5%)16+ 59,70/(1+1,5%)17= 73,82/1,015+72,94/1,03+72,06/1,05+71,17/1,06+70,29/1,08+69,41/1,09+68,53/1,11+67,64/1,13+66,76/1,14+65,88/1,16+65,00/1,18+64,11/1,20+63,23/1,21+62,35/1,23+61,47/1,25+60,58/1,27+59,70/1,29 = 72,73+70,82+68,63+67,14+65,08+63,68+61,74+59,86+58,56+56,79+55,08+53,43+52,26+50,69+49,18+47,70+46,28 = 999,65 у.е. = 73,82/(1+1,5%)1 + 72,94/(1+1,5%)2 + 72,06/(1+1,5%)3+ 71,17/(1+1,5%)4+ 70,29/(1+1,5%)5 + 69,41/(1+1,5%)6+ 68,53/(1+1,5%)7+ 67,64/(1+1,5%)8+ 66,76/(1+1,5%)9+ 65,88/(1+1,5%)10+ 65,00/(1+1,5%)11+ 64,11/(1+1,5%)12+ 63,23/(1+1,5%)13+ 62,35/(1+1,5%)14+ 61,47/(1+1,5%)15+ 60,58/(1+1,5%)16+ 59,70/(1+1,5%)17= 73,82/1,015+72,94/1,03+72,06/1,05+71,17/1,06+70,29/1,08+69,41/1,09+68,53/1,11+67,64/1,13+66,76/1,14+65,88/1,16+65,00/1,18+64,11/1,20+63,23/1,21+62,35/1,23+61,47/1,25+60,58/1,27+59,70/1,29 = 72,73+70,82+68,63+67,14+65,08+63,68+61,74+59,86+58,56+56,79+55,08+53,43+52,26+50,69+49,18+47,70+46,28 = 999,65 у.е. = 66,76/1,015+66,76/1,03+66,76/1,05+66,76/1,06+66,76/1,08+66,76/1,09+66,76/1,11+66,76/1,13+66,76/1,14+66,76/1,16+66,76/1,18+66,76/1,20+66,76/1,21+66,76/1,23+66,76/1,25+66,76/1,27+66,76/1,29 = 65,77+64,82+63,58+62,98+61,81+61,25+60,14+59,08+58,56+57,55+56,58+55,63+55,17+54,28+53,41+52,57+51,75 = 994,93 у.е. = 66,76/1,015+66,76/1,03+66,76/1,05+66,76/1,06+66,76/1,08+66,76/1,09+66,76/1,11+66,76/1,13+66,76/1,14+66,76/1,16+66,76/1,18+66,76/1,20+66,76/1,21+66,76/1,23+66,76/1,25+66,76/1,27+66,76/1,29 = 65,77+64,82+63,58+62,98+61,81+61,25+60,14+59,08+58,56+57,55+56,58+55,63+55,17+54,28+53,41+52,57+51,75 = 994,93 у.е. = 15/1,015+15/1,03+15/1,05+15/1,06+15/1,08+15/1,09+15/1,11+15/1,13+15/1,14+15/1,16+15/1,18+15/1,20+15/1,21+15/1,23+15/1,25+15/1,27+1015/1,29 = 14,78+14,56+14,29+14,15+13,89+13,76+13,51+13,27+13,16+12,93+12,71+12,5+12,4+12,2+12+11,81+786,82 = 998,74 у.е. = 15/1,015+15/1,03+15/1,05+15/1,06+15/1,08+15/1,09+15/1,11+15/1,13+15/1,14+15/1,16+15/1,18+15/1,20+15/1,21+15/1,23+15/1,25+15/1,27+1015/1,29 = 14,78+14,56+14,29+14,15+13,89+13,76+13,51+13,27+13,16+12,93+12,71+12,5+12,4+12,2+12+11,81+786,82 = 998,74 у.е.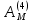 =0/1,015+0/1,03+0/1,05+0/1,06+0/1,08+0/1,09+0/1,11+0/1,13+0/1,14+0/1,16+0/1,18+0/1,20+0/1,21+0/1,23+0/1,25+0/1,27+1288,02/1,29 = 998,47 у.е. =0/1,015+0/1,03+0/1,05+0/1,06+0/1,08+0/1,09+0/1,11+0/1,13+0/1,14+0/1,16+0/1,18+0/1,20+0/1,21+0/1,23+0/1,25+0/1,27+1288,02/1,29 = 998,47 у.е.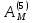 =67,08/1,015+67,08/1,03+67,08/1,05+67,08/1,06+67,08/1,08+67,08/1,09+67,08/1,11+67,08/1,13+67,08/1,14+67,08/1,16+67,08/1,18+67,08/1,20+67,08/1,21+67,08/1,23+67,08/1,25+67,08/1,27+67,08/1,29 = 66,09+65,13+63,89+63,28+62,11+61,54+60,43+59,36+58,84+57,83+56,85+55,90+55,44+54,54+53,66+52,82+52 = 999,71 у.е. =67,08/1,015+67,08/1,03+67,08/1,05+67,08/1,06+67,08/1,08+67,08/1,09+67,08/1,11+67,08/1,13+67,08/1,14+67,08/1,16+67,08/1,18+67,08/1,20+67,08/1,21+67,08/1,23+67,08/1,25+67,08/1,27+67,08/1,29 = 66,09+65,13+63,89+63,28+62,11+61,54+60,43+59,36+58,84+57,83+56,85+55,90+55,44+54,54+53,66+52,82+52 = 999,71 у.е.Таким образом, на основе представленных расчетов можно сделать вывод, что для кредитора наиболее предпочтительной будет являться схема 5, так как она обеспечивает максимум накопленной величины срочных уплат, то есть: 999,71 у.е. Для заемщика наиболее предпочтительной будет являться схема 2, так как она обеспечивает минимум накопленной величины срочных уплат, то есть: 994,93 у.е. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

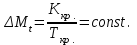

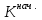 )
) )
)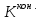 )
)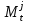

 ,
,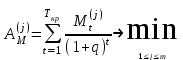 ,
,