Определить способом наименьших квадратов уравнение регрессии 1-го порядка вида y = a0 a1x. МНК. a1x и начертить его график
 Скачать 172.65 Kb.
|
|
2. Определить способом наименьших квадратов уравнение регрессии 1-го порядка вида y = a0 + a1x и начертить его график. Результаты измерения величин X и Y запишем в таблицу:
Нанесем эти значения на координатную плоскость, визуально исследуем расположение точек. Предполагая, что между X и Y существует линейная зависимость y = a0 + a1x, способом наименьших квадратов определим коэффициенты a0 и a1.  Для линейной зависимости  параметры a0 и a1 можно найти из системы уравнений: Переменная i изменяется от 1 до 3. Составим расчетную таблицу
Получаем систему  Откуда находим коэффициенты линейной функции. Решим систему с помощью формул Крамера. Найдем главный и вспомогательные определители системы:  ,  ,  .Следовательно, 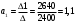  Таким образом, уравнение парной линейной регрессии имеет вид   В уравнении регрессии параметр a0 показывает усредненное влияние на результативный признак неучтенных в уравнении факторных признаков. Коэффициент регрессии a1 показывает, на сколько в среднем изменяется значение результативного признака при увеличении факторного признака на единицу собственного измерения. 3. Найти сумму квадратов отклонений точек теоретической линии регрессии от практических согласно заданию. Все расчеты будем проводить в таблице:
|