вопросы. Вариант 4 № 16. длина волны подключена к источнику синусоидального напряжения с частотой
 Скачать 377.67 Kb. Скачать 377.67 Kb.
|
|
Группа 4 по списку № 16 Однородная линия длиной  ( (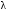 ‒ длина волны) подключена к источнику синусоидального напряжения с частотой ‒ длина волны) подключена к источнику синусоидального напряжения с частотой 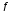 . Напряжение в конце линии . Напряжение в конце линии  . .Требуется: Для линии с распределенными параметрами (идеальной): Определить вторичные параметры линии: характеристическое (волновое) сопротивление 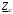 ; постоянную распространения ; постоянную распространения 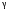 ; коэффициент затухания ; коэффициент затухания  ; коэффициент фазы ; коэффициент фазы  ; длину волны ; длину волны 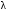 ; фазовую скорость ; фазовую скорость  . .Написать выражения для мгновенных значений напряжения и тока в начале линии, считая, что линия нагружена на характеристическое сопротивление 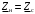 (согласованная нагрузка). (согласованная нагрузка).Построить годографы комплексов действующих значений напряжения и тока и кривые распределения действующих значений напряжения и тока вдоль линии (5 – 6 точек). Определить входное сопротивление линии при холостом ходе (х.х.) и коротком замыкании (к.з.). Принять в линии 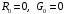 (идеальная линия). Для идеальной линии: (идеальная линия). Для идеальной линии:Вычислить характеристическое (волновое) сопротивление 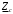 ; постоянную распространения ; постоянную распространения 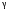 ; коэффициент затухания ; коэффициент затухания  ; коэффициент фазы ; коэффициент фазы  ; длину волны ; длину волны 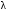 ; фазовую скорость ; фазовую скорость  . Результаты вычислений сравнить с расчетами реальной линии в табличной форме. . Результаты вычислений сравнить с расчетами реальной линии в табличной форме.Написать выражения для мгновенных значений напряжения и тока в начале идеальной линии при согласованной нагрузке. Построить кривые распределения действующих значений напряжения и тока вдоль линии. Определить входное сопротивление идеальной линии при холостом ходе (х.х.) и коротком замыкании (к.з.) для двух значений длины линии:  Рассчитать и построить кривые распределения действующих значений напряжения и тока вдоль линии при холостом ходе (х.х.) и коротком замыкании (к.з.) (стоячие волны). Провести расчет линии без искажений, для чего: Проверить, соблюдается ли условие Хевисайда для данной реальной линии. (Условие Хевисайда :  ). ).При несоблюдении условия Хевисайда путем изменения индуктивности 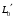 , а затем – емкости , а затем – емкости 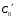 (рассчитать их), определить напряжение и ток в начале линии при согласованной нагрузке и рассчитать вторичные параметры линии без искажений для измененных (рассчитать их), определить напряжение и ток в начале линии при согласованной нагрузке и рассчитать вторичные параметры линии без искажений для измененных 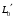 и и 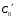 . Сделать вывод (анализ по расчету). . Сделать вывод (анализ по расчету).Решение: 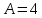 ; ;   = = m=5; n=1; p=6  ; ;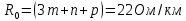 ; ;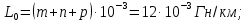  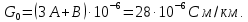 Однородная линия длиной Ɩ  подключена к источнику синусоидального напряжения с частотой подключена к источнику синусоидального напряжения с частотой  . Напряжение в конце линии . Напряжение в конце линии  . Параметры линии: . Параметры линии: 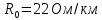 ; ; 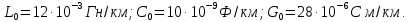 Расчет реальной линии с распределенными параметрами Частота угловая:  ; ;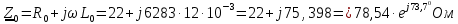 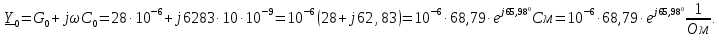 Характеристическое сопротивление:  Коэффициент распространения: 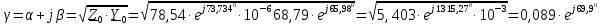 = = 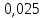 +j 0,069 +j 0,069откуда  , ,  Длина волны:  . .Фазовая скорость  Мгновенные значения напряжения и тока в начале линии имеют вид:  Частота  . . Напряжение и ток в начале линии выражаются уравнениями: 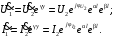 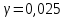 +j0,069, y= +j0,069, y= y – расстояние от конца линии. Поскольку требуется записать мгновенные значения в начале линии, то y = l (l – длина линии). Рассчитаем:  В; В; . . 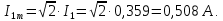 Мгновенные значения напряжения и тока в начале линии: 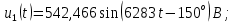 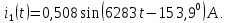 Для построения годографов и графиков воспользуемся полученными уравнениями. Разобьем линию на 5 частей и проведем расчет для каждой точки:  км. Для каждой точки линии длиной км. Для каждой точки линии длиной 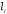 : :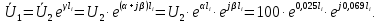 Тогда: действующее значение напряжения  фаза напряжения в радианах 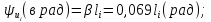 фаза напряжения в градусах 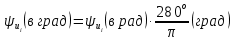 действующее значение тока  ; ;фаза тока в градусах  . .Для рассматриваемой линии расчеты в Mathcad: Таблица 1 ‒Расчет комплексов напряжения и тока реальной линии
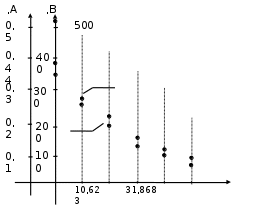
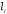 ‒ расстояние от конца линии. ‒ расстояние от конца линии.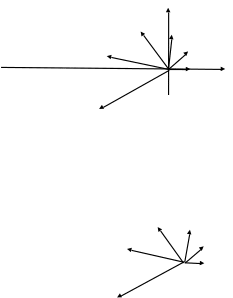 Далее строим годографы тока и напряжения (рис.1, рис. 2) и кривые распределения действующих значений напряжения и тока (рис. 3) вдоль линии. Далее строим годографы тока и напряжения (рис.1, рис. 2) и кривые распределения действующих значений напряжения и тока (рис. 3) вдоль линии.
 Рис. 1 –Годограф комплексных значений напряжений вдоль линии Рис. 1 –Годограф комплексных значений напряжений вдоль линии
Рис. 2 –Годограф комплексных значений тока вдоль линии
Рис. 3 –Распределение действующих значений напряжения и тока вдоль линии Рассчитаем: 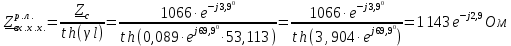 ; ;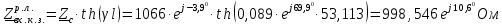 . .Расчет идеальной линии с распределенными параметрами У идеальной линии  = = С учетом этих соотношений рассчитываем вторичные параметры линии: Характеристическое сопротивление:  Коэффициент распространения:  , откуда коэффициент затухания , откуда коэффициент затухания  , коэффициент фазы , коэффициент фазы  Длина волны:  км. км.Фазовая скорость 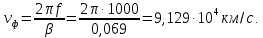 Длина линии 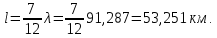 Таблица 2. ‒Сравнение параметров реальной и идеальной линии
Для идеальной линии напряжение и ток в начале линии определяются уравнениями: 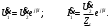  , y = l = , y = l =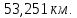 y – расстояние от конца линии. Поскольку требуется записать мгновенные значения в начале линии, то y = l (l – длина линии). Рассчитаем:  В; В; . .Мгновенные значения напряжения и тока в начале линии: 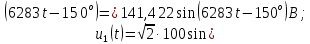 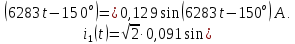 Действующие значения напряжения и тока в идеальной линии и при согласованном режиме не зависят от длины линии и остаются постоянными (рис. 4). 
Рис. 4 –Распределение действующих значений напряжения и тока вдоль идеальной линии Сначала проводим расчет при   ; ;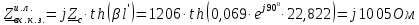 . .Затем ‒ при 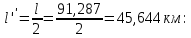 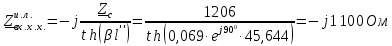 ; ; . .При холостом ходе уравнения стоячих волн имеют вид  Проводим расчеты для некоторых значений расстояния от конца линии:      Результаты занесем в таблицу 3. Таблица 3 ‒ Расчет стоячих волн напряжения и тока при х. х.
По результатам расчета строятся графики стоячих волн напряжения и тока при холостом ходе линии (рис. 5). При коротком замыкании уравнения стоячих волн имеют вид: 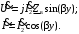 Подставим вычисленные значения: 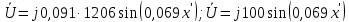 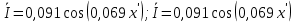 Проведем расчет для нескольких значений:  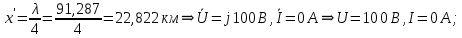  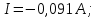  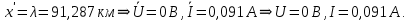 Результаты занесем в таблицу 4. Таблица 4. ‒Расчет стоячих волн напряжения и тока при к. з.
По результатам расчета строим графики стоячих волн напряжения и тока при холостом ходе линии (рис. 6). 
Рис. 5 –Распределение действующих значений напряжения и тока вдоль идеальной линии при холостом ходе 
Рис. 6 –Распределение действующих значений напряжения и тока вдоль идеальной линии при коротком замыкании Расчет идеальной линии без искажений Проверим условие Хевисайда: 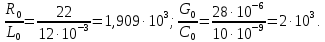 Условие не соблюдается. Для соблюдения условия Хевисайда необходимо, чтобы значение индуктивности  . .Проведем расчет вторичных параметров линии без искажений при  . .Характеристическое сопротивление:  Коэффициент распространения: 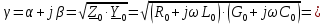 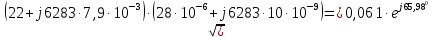 = 0,025+j0,056 = 0,025+j0,056откуда  , ,  Длина волны:  Фазовая скорость 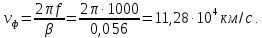 Длина линии  Напряжение и ток в начале линии: 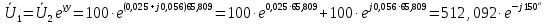 В; В; . .Аналогично проводится расчет, если для соблюдения условия Хевисайда изменить емкость 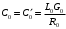 , а индуктивность оставить заданной. , а индуктивность оставить заданной.3.3 Для соблюдения условия Хевисайда необходимо, чтобы значение ёмкости  . .Проведем расчет вторичных параметров линии без искажений при 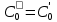 . .Характеристическое сопротивление:  Коэффициент распространения: 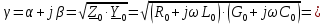 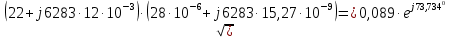 =0,025+j =0,025+j откуда  , ,  Длина волны:  Фазовая скорость 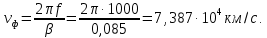 Длина линии 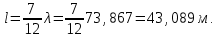 Напряжение и ток в начале линии:  В; В;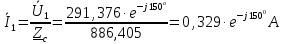 . .   |

 , В
, В в рад.
в рад. , А
, А в градусах
в градусах




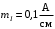



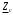 , Ом
, Ом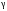
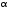 , Нп/км
, Нп/км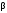 , рад/км
, рад/км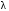 , км
, км ,км/с
,км/с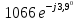

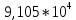
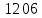



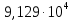


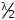
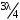
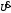 , В
, В , А
, А