Теория телетрафика. Курсовая работа Теория телетрафика. " методы оценки качества функционирования систем распределения информации "

• Название: " методы оценки качества функционирования систем распределения информации "
• Анкор: Теория телетрафика
• Дата: 23.04.2022
• Размер: 353.5 Kb.
• Имя файла: Курсовая работа Теория телетрафика.doc
• Тип: Курсовая; #491478

Министерство РФ по связи и информатизации
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов

Курсовая работа по предмету Теория телетрафика

На тему: " методы оценки качества функционирования систем распределения информации "

Выполнил:

Группа:СДТ-44

Проверил: ___________________


Вариант №9

(Номер варианта задания определяется по сумме двух последних цифр номера пароля.)
Задача 1.

На коммутационную систему поступает поток вызовов, создающий нагрузку Y эрланг. Определить вероятности поступления ровно i вызовов P_i (i=0, 1, 2 ...N) при примитивном потоке от N источников и P_i ( i=0,1, 2...j...) при простейшем потоке вызовов. Построить кривые распределения вероятностей P_i =f ( i ) и произвести сравнение полученных результатов. Величины Y и N приведены в таблице

Номер варианта	9
Y, эрл	1,5
N	5

Решение:

Примитивный поток вызовов - такой симметричный поток, параметр которого прямо пропорционален числу свободных в данный момент источников нагрузки. Вероятность поступления вызовов Pi для такого потока рассчитывается по формуле Бернулли:

, где

- число сочетаний из N источников по i вызовов.

- нагрузка от одного источника

Сведем расчет в таблицу №1:

Таблица №1.

N	0	1	2	3	4	5
Pi	0.1681	0.3602	0.3087	0.1323	0.0284	0.0024

Простейший поток - поток от бесконечно большого числа источников нагрузки (практически, для расчетов достаточно, чтобы число вызовов N было больше 100). Вероятность поступления i вызовов для простейшего потока рассчитывается по формуле Пуассона:

, где

P_i - вероятность того, что в произвольный момент времени t бесконечный пучок находится в состоянии i.

Сведем расчет в таблицу №2:

Таблица №2.

N	0	1	2	3	4	5
Pi	0.22313	0.334695	0.251021	0.125511	0.047067	0.01412

По результатам проведенных расчетов производим построение кривых распределения вероятностей P_i = f(i) на рисунке №1: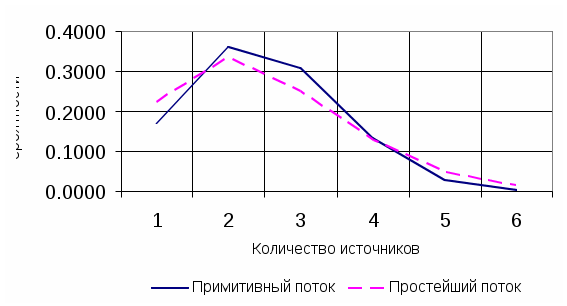



Рис.1. Кривые распределения вероятностей примитивного и простейшего потока.
Вывод:

Вероятность поступления 2-х вызовов наибольшая, причем для примитивного потока больше чем для простейшего. При увеличении числа источников примитивный поток стремится к простейшему.
Задача 2.

Пучок ИШК координатной станции типа АТСК -У обслуживает абонентов одного блока АИ. Определить поступающую на этот пучок нагрузку Y, если число абонентов, включенных в блок, N=1000, среднее число вызовов от одного абонента С, среднее время разговора Т , доля вызовов закончившихся разговором P_P . значения с, Т и P_P приведены в таблице. Нумерация на сети пяти- или шестизначная.

Номер варианта	9
c, выз/час	2,5
T, c	140
PP	0,55

Решение:

Исходя из условия задачи, необходимо учесть состоявшиеся разговоры, из всех возможных исходов поступившего вызова. Следовательно, расчет необходимо производить по формуле:

, где Y- поступающая на пучок нагрузка;

- 2.5 выз/ч. - среднее число вызовов в час поступающее от одного абонента;

N=1000 абонентских линии (АЛ) - число источников нагрузки;

- средняя длительность занятия;

- средняя длительность занятия при состоявшемся разговоре;

- доля вызовов заканчивающихся разговором;

- средняя длительность занятия при несостоявшемся разговоре из-за занятости линии абонента;

- доля вызовов, несостоявшихся из-за занятости линии вызываемого абонента;

- средняя длительность занятия при несостоявшемся разговоре из-за ошибки набора;

- доля вызовов несостоявшихся из-за ошибки вызывающего абонента разговором;

t_тех - средняя длительность занятия при несостоявшемся по техническим причинам разговоре;

P_тех - доля вызовов с несостоявшимся технической причине разговором;

 - коэффициент непроизводительного занятия, зависящий от продолжительности разговора и нумерации в сети;

для сети с шестизначной нумерацией при =140 с и Р_р=0.55 ,  находим по графику - рис 3.3 [1]. =1,13;
, где

= t_н m

t_н=1,5 – время набора одной цифры. Завод диска  1 с. Возвращение  0.5 с.

m=6 - число знаков абонентского номера



=3 c - средняя продолжительность слушания абонентом сигнала «ответ станции»;

- средняя продолжительность посылки вызова вызывающему абоненту.

=140 с - среднее время разговора.

с - время установления соединения после набора последней цифры и время разъединения соединения для АТСК.

Рассчитываем среднее время состоявшегося разговора , подставляя данные в формулу 3.8 [1]:



Чтобы вычислить нагрузку в Эрлангах, необходимо разделит результат вычисления формулы 3.13 [1] на 1 час=3600 с, в конечном итоге формула расчета нагрузки принимает следующий вид:


эрл.
Ответ: Поступающая на пучок нагрузка составляет 70,135 Эрланг.
Задача 3.

Полнодоступный пучок из V линий обслуживает поток вызовов. Определить пропускную способность пучка, т.е. нагрузку Y , которая может поступать на этот пучок при заданной величине потерь по вызовам P_В в случае простейшего потока и примитивного потока от N₁ и N₂ источников. Значения V, P_B, N₁ и N₂ приведены в таблице. По результатам расчета сделать выводы.

Номер варианта	9
V	4
PB,%0	10
N1	20
N2	10

Решение:

Простейшим потоком называется стационарный, ординарный поток без последействия.
Поток вызовов является стационарным, если при любом числе отрезков времени n совместный закон распределения числа вызовов К за промежутки времени
(t_O, t₁), (t_O, t₂), ... (t_O, t_n)

P{K(t_O, t₁), {t_O, t_i, i=1, 2, ..., n}}
зависит только от длины промежутков времени и не зависит от длины промежутков времени и не зависит от момента t₀.

То есть, независимо от того, где на оси времени расположен промежуток времени (t_O, t₁), вероятность поступления K(t_O, t₁) вызовов одна и та же.
Поток вызовов является ординарным, если при интервале времени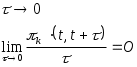



т.е. , где - величина более высокого порядка малости по отношению к . Где - вероятность поступления k и более вызовов в любой момент времени t.
Поток вызовов является потоком без последействия, если вероятность поступления K(t_o, t_i) вызовов за промежутки
(t_O, t_i), i=1, 2, ..., n

P{K(0, t₁)- K(0, t₀) = K(t₀, t₁), i=1, 2, ..., n}
не зависит от вероятностного процесса поступления вызовов до момента t_0.
Другими словами, отсутствие последействия потока - это независимость течения случайного течения потока вызовов после какого либо момента времени от его течения до этого момента.

Простейший поток вызовов - наиболее распространенная модель реального потока вызовов.

Обслуживание полнодоступным пучком простейшего потока описывается первой формулой Эрланга: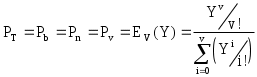



Для простейшего потока потери равны между собой.

Y находим по графику функции Эрланга (Приложение1 [2]):
Y  0,87

Примитивный поток.

Примитивным называется симметричный поток, параметр которого _i прямо пропорционален числу свободных в данный момент источников
_i=(N-i) , где

i - число занятых источников;

 - параметр потока источников в свободном состоянии (занятый источник не может производить вызовы.)
Симметричным потоком называется поток с простым последействием, параметр которого _S(t) в любой момент времени t зависит только от числа i, обслуживаемых в этот момент вызовов и не зависит от других характеристик, определяющих состояние S(t) коммутационной системы. При этом зависимость параметра от числа обслуживаемых вызовов может быть подчинена любому закону. Поэтому в любом состоянии St с i обслуживаемыми вызовами параметр симметричного потока один и тот же, он зависит только от i, т.е. _S(t)=_i.
Поток с простым последействием - ординарный поток, для которого в любой момент времени t существует конечный параметр потока в состоянии S(t), зависящий только от состояния S(t) коммутационной системы в момент t и независящий от процесса обслуживания вызовов до момента t.
Под параметром потока S(t) понимают предел: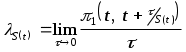

, где

- вероятность поступления за промежуток одного и более вызовов, если в момент t коммутационная система находится в состоянии S(t).
Обслуживание полнодоступным пучком примитивного потока описывается формулой Энгсета

, i =0, 1, 2, ..., U.

где P_i - вероятность того, что в пучке емкостью U линий, включенном в не блокирующую коммутационную систему с потерями и обслуживающем вызовы примитивного потока, в любой произвольный момент времени занято i линий.
Так как задачу невозможно решить по Y, то используем данные, приведенные в Приложении 2 [2], по которым можно при заданном числе источников N найти

a - нагрузку, поступающую от 1-го источника, после чего легко высчитать Y по формуле:

Y =aN

табулированная формула: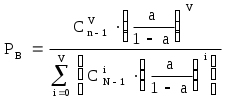



При V=4 ; P_B,%₀=10; N1=20 находим а=0,05 Эрл.

Y= a  N = 0.05  20=1 Эрланг
При V=4 ; P_B,%₀=10; N2=10 находим а=0,11 Эрл.

Y= a  N = 0.11  10=1.1 Эрланг

Вывод:

При увеличении числа источников в полнодоступном пучке с заданным количеством каналов при примитивном потоке приближается к нагрузке простейшего потока вызовов, созданная ими нагрузка к простейшему потоку.
Задача 4.

На коммутационный блок координатной станции типа АТСК поступает простейший поток вызовов, который создает нагрузку Y_б эрланг при средней длительности занятия входа блока t_б . Блок обслуживается одним маркером, работающим в режиме с условными потерями при постоянной длительности занятия t_м.

Задержанные вызовы обслуживаются в случайном порядке независимо от очередности поступления.

Определить вероятность ожидания свыше допустимого времени t_д и среднее время ожидания задержанных вызовов t_{з .} Значения Y_б , t_б, t_м и t_{д .} приведены в таблице

Номер варианта	9
Yб, эрл	40
tб, с	80
tм, с	0,8
tд,с	2,4

Решение:
Исследование систем, работающих в режиме маркеров АТСК, было проведено Берком, который выявил зависимость вероятности задержки Р_з свыше времени t:
Р_з(>t) = e^-(v-y)t, где
 -- постоянная занятия

V – число каналов

у – нагрузка

t – время допустимой задержки.
Среднее время ожидания задержанных вызовов:


На практике чаще всего пользуются формулой
t_з = t_м  _з , где
t_м – постоянная длительности занятия, заданна по условию

- время в единицах длительности занятия, находится по графику, в зависимости от нагрузки на маркер у_м, которая находится по формуле:

, где

t_б – средняя длительность занятия входа коммутационного блока (КБ) АТСК;

у_б – нагрузка на КБ от простейшего потока вызовов.
Нагрузка маркера:

у_м = Эрл.
При такой нагрузке _з = 0,87.

Рассчитываем время допустимой задержки вызовов



t_з = 0,8  0,87 = 0,696 с.
Время, после которого будут теряться вызова (в условных единицах):

, где

t_д – допустимое время ожидания вызовов.
Очевидно, что это время t равно количеству обслуживаемых без потерь вызовов, выбранных в произвольном порядке, то есть без очереди. Остальные вызовы (х>t) теряются.

Рассчитаем t:

.

Вероятность ожидания вызова свыше допустимого времени t – р(>t) найдем по рис.2 (Приложение 3 [2])

P(>3) = 0,5

Задача 5.

Нагрузка, поступающая на ступень ГИ АТСК, обслуживается в данном направлении пучком линий с доступностью K_Bq при потерях P=0,005. Нагрузка на один вход ступени а, нагрузка в направлении y . Определить методом эффективной доступности емкость пучка V при установке на ступени блоков 60х80х400 и 80х120х400. Сравнить полученные результаты. Величины K_Bq , y, a приведены в таблице

Номер варианта	9
KBq	20
y, Эрл	33
а, Эрл	0,49

Решение:
Задача решается по методу эффективной доступности, пригодному как для ПД так и для НПД двухзвенных схем. Он основан на переменной доступности. Когда нет занятых соединительных путей (линий), каждому входу 1 ступени ГИ доступен любой выход требуемого 2 ступени, доступность выходов данного направления максимальна (все выходы доступны).
При q = 1 доступность равна m.

d_max = mq – стр. 153 [1].
При наличии i занятых ПЛ (промежуточных линий) для всех входов в коммутатор, имеющий занятые i, доступность уменьшится на iq и будет равна:
d_i = (m - i)q, где
m – число выходов 2 ступени;

n – число входов 1 ступени;

q – число выходов из одного коммутатора в направлении искания: .

Минимальная доступность рассматриваемого направления для сжатия (n>m) равна 0, т.к. для (m + 1) занятия на входе коммутатора из-за занятости всех m ПЛ невозможно подключение к к.л. выходу.

Для схем с расширением или без расширения и сжатия (nm) минимальная доступность больше 0 и равна:
d_min = (m - n + 1)  q – ф. 9.23 [1].
В процессе работы двухзвенной схемы в режиме ГИ доступность выходов d_iменяется в пределах:
d_min d_i d_max – ф. 9.24 [1].
Для двухзвенной схемы существует эквивалентная схема (по потерям) однозвенного включения НПД. Доступность такой схемы называется эффективной доступностью d_э. Определяется формулой:
d_min < d_э < d_max – ф. 9.27 [1];
и формулой -- 9.27 [1], где

 -- коэффициент, определяемый зависимостью потерь от доступности и распределением вероятностей доступности W_i;

-- математическое ожидание доступности.

 = 0,65  0,75

d_min -- минимальная доступность, определяется соотношением: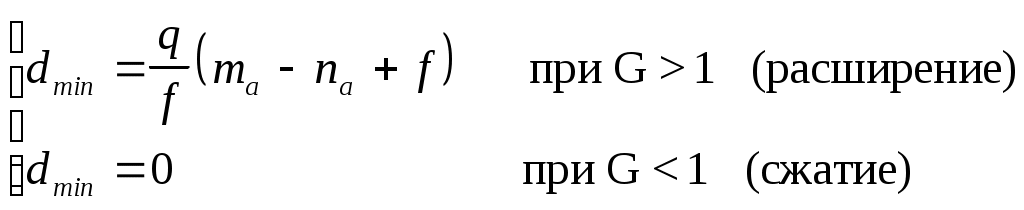

где f - связность.
при f =1 одно связности

при f=2
где Y_м - интенсивность нагрузки, обслуженной m ПЛ, рассчитывается по формуле:

Ym = an_a , где
а =0.49 Эрл. - нагрузка, создаваемая одним источником в единицу времени

m_a и n_а - структурные параметры коммутатора.
Примем для блока 6080400 :

=0.7 n_a=15; m_a=K_B=20; f=1

для блока 80120400:

=0.7, n_a=13,33; m_a=K_B=20; f=1

q=1
Для 60х80х400:







V = У+, где

согласно таблице коэффициентов приложение 4 [2] =1.62, =3.6

V = 1.62  33+3.6 =57.06  57 линий.
Для 80120400:









V = У+, где

=1.55, =3.9

V = 1.55  33+3.9 =55.05  55 линий.
Вывод:
С увеличением числа промежуточных линий, число требуемых соединительных линий, подключенных к выходу коммутационного блока, уменьшается.

Задача 6.

На вход ступени ГИ АТС поступает нагрузка по двум пучкам линий, математическое ожидание которой Y₁ и Y₂. На выходе ступени объединенная нагрузка распределяется по направлениям пропорционально коэффициентам K_i . определить расчетное значение нагрузки каждого направления и относительное отклонение расчетного значения нагрузки от ее математического ожидания. По результатам расчета сделать вывод. Исходные данные приведены в таблице

Номер варианта	9
Y1, Эрл.	20
Y2, Эрл.	30
K1	0,1
K2	0,2
K3	0,3
K4	0,4

 

Решение:
При расчете объема оборудования с нормированными потерями Р по математическому ожиданию нагрузки У будут меньше или равны Р с вероятностью 0,5 – в 50% всех часов наибольшей нагрузки (ЧНН), так как интенсивность нагрузки, создаваемой группой источников, колеблется по ЧНН разных дней.

Поэтому для расчета заданного качества обслуживания с большей вероятностью объем оборудования выполняют не по математическому ожиданию У интенсивности нагрузки, а по расчетной интенсивности нагрузки ф. 10.45 [1] У_р:
У_р = У + Z(У), где
Z – аргумент функции Лапласа, учитывающий объем оборудования, на практике его принимают Z = 0,6747

(У) – дисперсия нагрузки; (У) = ²(У), где ²(У) – дисперсия нагрузки.
Для простейшего потока вызовов математическое ожидание интенсивности нагрузки равно дисперсии нагрузки: (У) = .

Поэтому:

У_р = У + Z
Подставив числовые значения, рассчитаем У_pi.

У = У₁ + У₂ – общее значение математического ожидания нагрузки, поступающей по двум пучкам линий на вход ГИ.

У = 20+30 = 50 Эрл.
Так как на выходе ступени ГИ объединенная нагрузка распространяется по направлениям пропорционально коэффициентам К_i, то У_i = К_i  У

У₁ = У  К₁ = 500.1 = 5 Эрл

У₂ = У  К₂ = 500.2 = 10 Эрл

У₃ = У  К₃ = 500.3 = 15 Эрл

У₄ = У  К₄ = 500.4= 20 Эрл
Подставив числовые значения, рассчитаем:

У_pi = У_i + 0.6747 

У_p1 =5 + 0.6747  = 6.5 Эрл

У_p2 =10 + 0.6747  = 12.13 Эрл

У_p3 =15 + 0.6747  =17.61 Эрл

У_p4 =20 + 0.6747  = 23.02 Эрл

Переход от расчетного значения к математическому ожиданию нагрузки осуществляется по формуле


= 4,99 Эрл

=9,99 Эрл

= 15 Эрл

= 20 Эрл

Отклонение расчетной нагрузки от ее математического ожидания нагрузки:

, где

У_pi – расчетное значение в направлении i

У_i – математическое ожидание значения нагрузки в направлении i.







Вывод:
С увеличением нагрузки, ее отклонение уменьшается, что говорит о том, что нагрузка более равномерно распределяется в ЧНН.

Литература.

1. Б. С. Лившиц, А. П. Пшеничников, А. Д. Харкевич. Теория телетрафика. Учебник для электротехнических институтов связи. М. «Связь» 1979 г.

2. Методические указания и задание на курсовую работу СибГУТИ