Дискретная математика. множество натуральных чисел. Определить истинное высказывание

• Название: множество натуральных чисел. Определить истинное высказывание
• Дата: 15.04.2023
• Размер: 0.91 Mb.
• Имя файла: Дискретная математика.doc
• Тип: Документы; #1063835
• страница: 2 из 4

32. 
    
    

Для предиката P(x,y)=(x+y)=0, заданного на множестве действительных чисел, укажите набор значений кванторов , :

1,0

0,0

1,1

0,1

33. 
    
    

Для сетевого графа, соответствующего некоторому проекту, критический путь представляет собой:

путь минимальной длины от входа к выходу;

путь произвольной длины от входа к выходу.

путь максимальной длины от входа к выходу;

34. 
    
    

Для сетевого графа, соответствующего некоторому проекту, скорейшее время завершение всего проекта совпадает с длиной:

максимального пути от входа к выходу;

произвольного пути от входа к выходу.

минимального пути от входа к выходу;

35. 
    
    

Если высказывания эквивалентны, существуют ли между ними отношения следствия?

существуют;

могут существовать, а могут и не существовать.

не существуют;

36. 
    
    

Если из высказывания S1 следует S2 и наоборот из S2 следует S1 , являются ли высказывания S1 и S2 эквивалентными?

не являются;

могут являться, а могут и нет.

являются;

37. 
    
    

Если к некоторому бесконечному множеству M прибавить счетное множество A, то в каком соотношении будут находиться мощности множеств и M?

мощность множества M меньше мощности множества ;

мощность множества M равна мощности множества ;

мощность множества M больше мощности множества ;

38. 
    
    

Если матрица смежности симметрична, то граф является:

ориентированным с петлями.

неориентированным;

ориентированным с нечетным числом дуг;

39. 
    
    

Если на главной диагонали матрицы смежности стоит единица, то:

из данной вершины выходит дуга, заканчивающаяся в другой вершине;

в данной вершине находится петля.

в данную вершину входит дуга, начинающаяся в другой вершине;

40. 
    
    

Если отношение А на множестве М рефлексивно, симметрично и транзитивно, можно ли разбить множество М на непересекающиеся классы?

да;

можно, но не всегда.

нет;

41. 
    
    

Если при проверке правильности рассуждения получен результат , где P – конъюнкция посылок, Q – заключение, то, в таком случае, данное рассуждение является:

может быть правильным, а может быть и неправильным.

неправильным;

правильным;

42. 
    
    

Если СДНФ формулы S(X1,X2,X3) содержит 3 слагаемых, сколько сомножителей содержит ее СКНФ?

5.

4;

3;

43. 
    
    

Задано отображение множества в множество : , , , . Отображение будет являться:

инъективным;

биективным.

сюръективным;

44. 
    
    

Как присваиваются метки вершинам ориентированного графа при нахождении пути по алгоритму Форда:

.

;

;

45. 
    
    

Какие из высказываний , состоящих из двух элементарных высказываний А и В, равносильны? : "Если А, то не В". : "А или не В". : "Неверно, что А и В".

S1=S2

S2=S3

S1=S3

46. 
    
    

Какие из пар связок образуют полную систему связок?

.

;

;

47. 
    
    

Какие переменные в предикате являются свободными?

;

.

;

48. 
    
    

Какие переменные в предикате являются связными?

;

.

;

49. 
    
    

Каково значение X, определяемое уравнением ?

;

;

.

50. 
    
    

Каково число слагаемых СДНФ формулы ?

;

.

n;

51. 
    
    

Какое свойство не является свойством дерева?

граф связен и все его ребра являются перешейками;

граф связен и содержит циклы.

всякая пара вершин графа соединена только одной цепью;

52. 
    
    

Какой граф называется сетью?

несвязный граф, компонентами связности которого являются деревья;

неориентированный граф с одним входом;

ориентированный граф с циклами;

ориентированный граф без циклов с одним входом и одним выходом.

53. 
    
    

Какой граф обладает эйлеровым циклом: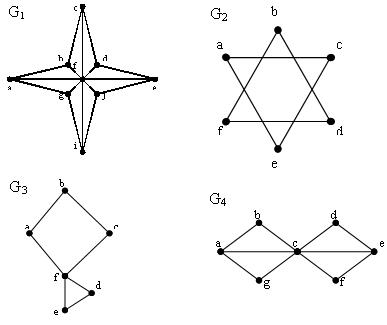

G4

G2

G1

G3

54. 
    
    

Какой граф содержит эйлерову цепь, соединяющую две различные вершины: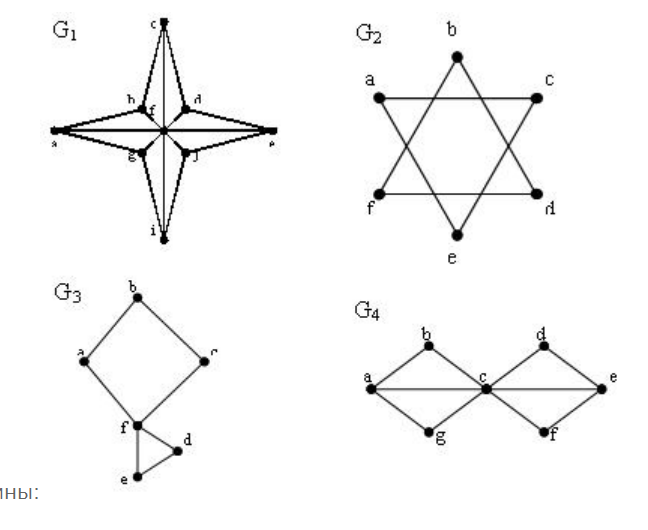

G2

G4

G1

G3

55. 
    
    

Какой граф, соответствует данной матрице смежности?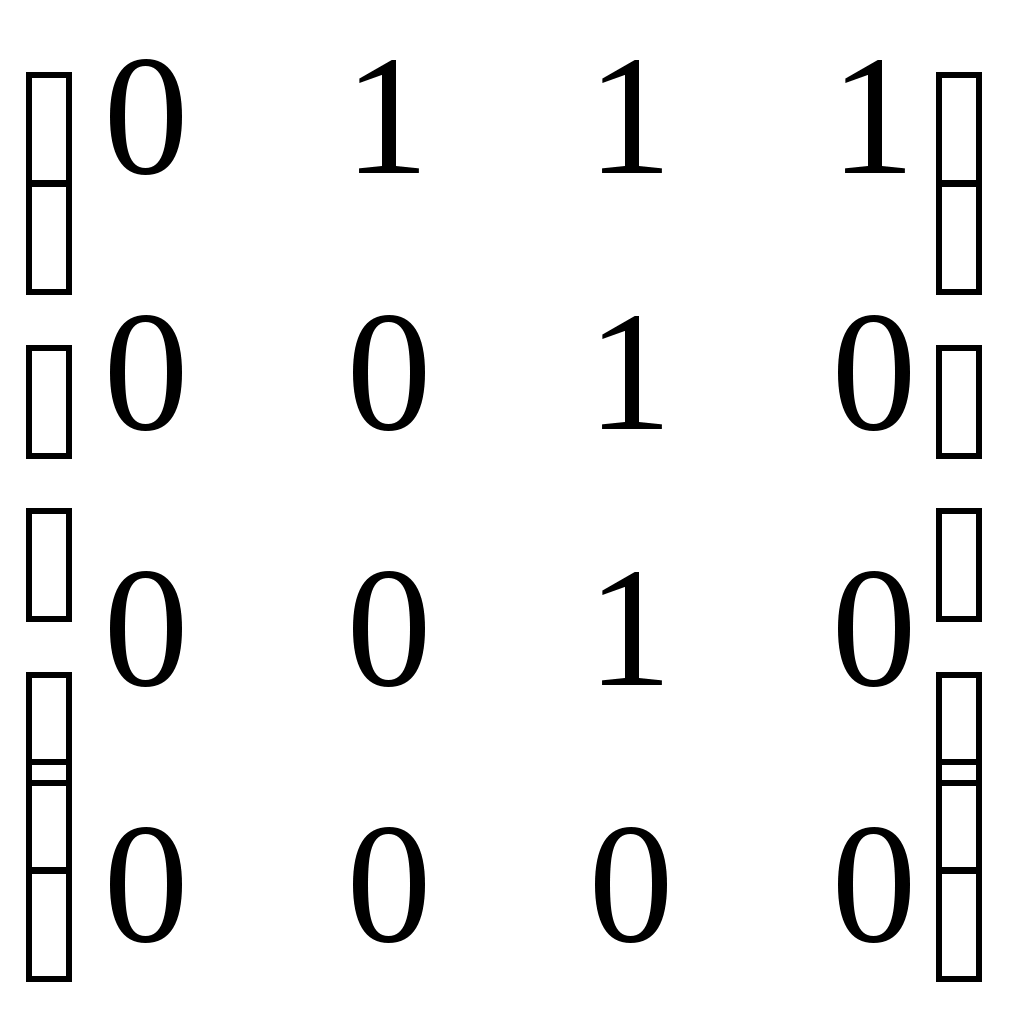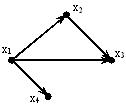

56. 
    
    

Какой из данных графов правильно пронумерован?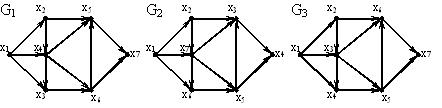

G1

G3

G2

57. 
    
    

Какой из данных графов является деревом?

G3

G1

G2

58. 
    
    

Какой из данных графов является планарным?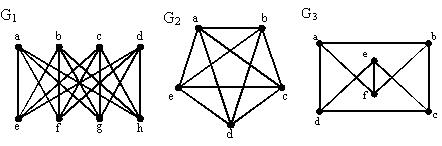

G3

G2

G1

59. 
    
    

Какой из данных графов является сетью?

G2

G3

G1

60. 
    
    

Количество «единичных» значений таблицы истинности формулы :

0;

3.

5;

61. 
    
    

Количество «нулевых» значений таблицы истинности формулы

3.

5;

0;

62. 
    
    

Логической функции соответствует формула алгебры высказываний:

.

;

;

63. 
    
    

Логической функции , соответствует формула алгебры высказываний:

.

;

;

64. 
    
    

Матрица смежности для графа имеет вид: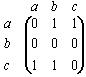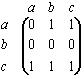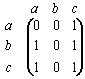

65. 
    
    

Минимальная полная система логических связок содержит:

одну связку;

четыре связки.

две связки;

три связки;

66. 
    
    

Могут ли быть при правильном рассуждении все посылки истинными, если заключение ложно?

да;

иногда да, иногда нет.

нет;

67. 
    
    

Могут ли две релейно-контактные схемы, соответствующие одной и той же функции проводимости, иметь различное число реле?

нет;

никогда не могут.

да;

68. 
    
    

Могут ли равносильные высказывания быть записаны в виде некоторой релейно-контактной схемы?

могут, но не всегда.

не могут;

могут;

69. 
    
    

Может ли сюръективное отображение являться инъективным?

может являться, но может и нет.

никогда;

всегда;

70.