Дискретная математика. множество натуральных чисел. Определить истинное высказывание
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
|
Можно ли в любом бесконечном множестве выделить счетное подмножество? | можно; можно, но не всегда. нельзя; | |
| | Можно ли для функции F(S1,S2,S3) заданной так, что на всех наборах значений переменных S1,S2,S3 она принимает значение 0, построить какую-либо совершенную нормальную форму? | можно СКНФ; нельзя построить ни одной совершенной нормальной формы. можно СДНФ; |
| | Можно ли некоторое высказывание записать в виде релейно-контактной схемы? | нет; иногда можно, иногда нет. да; |
| | Мощность какого множества больше X или Y, если X – исходное конечное множество, Y – множество подмножеств множества X? | мощность X равна мощности Y. мощность X больше мощности Y; мощность X меньше мощности Y; |
| | На каком графе выделен частичный граф-дерево: 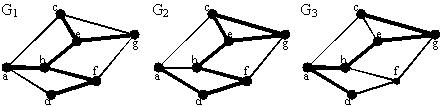 | G2 G3 G1 |
| | На множестве всех треугольников на плоскости рассматривается отношение подобия. Данное отношение является отношением: | эквивалентности. толерантности; порядка; |
| | Несвязный граф, компонентами связности которого являются деревья, называется: | лесом. частичным графом; сетевым графом; прадеревом; |
| | Обладает ли эйлеровым циклом полный неориентированный граф с числом вершин n=4? | да; зависит от числа дуг. нет; |
| | Обладает ли эйлеровым циклом полный неориентированный граф с числом вершин n=5? | нет; зависит от числа дуг. да; |
| | Обладают ли свойством двойственности формулы поглощения? | нет; одна обладает, другая нет. да; |
| | Определите значение следующего выражения | 0 1 |
| | Определите значение следующего выражения | 0 1 |
| | Определите минимальное число ребер, которое нужно удалить, чтобы граф стал древом: 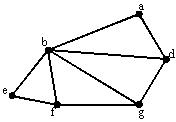 | 1 4 5 |
| | Определите минимальное число ребер, которое нужно удалить, чтобы граф стал древом: 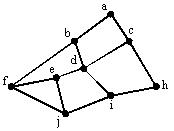 | 4 1 5 |
| | Определите существенные переменные логической функции | z y x |
| | Определите фиктивные переменные логической функции | x z y |
| | Определите, каким отношением следования связаны предикаты | не связаны. |
| | Определить форму следующей формулы | не СДНФ и не СКНФ. СКНФ; СДНФ; |
| | Определить форму следующей формулы | КНФ; не ДНФ и не КНФ. ДНФ; |
| | Определить форму следующей формулы | не СДНФ и не СКНФ. СКНФ; СДНФ; |
| | Определить форму следующей формулы | не СДНФ и не СКНФ. СКНФ; СДНФ; |
| | Отношение "y кратно x", заданное на множестве положительных целых чисел, является: | антирефлексивным; антисимметричным. симметричным; |
| | Отношение "быть старше": "х старше у" является: | симметричным; транзитивным. рефлексивным; |
| | Отношение "х – победитель у" является: | антирефлексивным; транзитивным. симметричным; |
| | Отношение | транзитивности. рефлексивности; симметричности; |
| | Отношение | толерантности; эквивалентности. порядка; |
| | Отношение равенства площадей, заданное на множестве всех треугольников на плоскости является отношением: | порядка. эквивалентности; толерантности; |
| | Почему множество действительных чисел и множество натуральных чисел не являются эквивалентными? | не существует биективного отображения между этими множествами. множество действительных чисел неупорядочено; множество натуральных чисел неупорядочено; |
| | Предикат "1=0" является: | бинарным. тернарным; 0-местным; унарным; |
| | Пусть | (6n); |
| | Пусть | |
| | Пусть | К=0. К=1; К=2; |
| | Пусть | К=1; К=0. К=-1; |
| | Пусть на множестве M задано отношение A: "х знаком с у". Почему на основе данного соотношения нельзя разбить множество M на непересекающиеся классы? | отношение A не транзитивно. отношение A не симметрично; отношение A не рефлексивно; |
| | Результат дизъюнкции предикатов P(X)=(X > 2) и Q(X)=(X < 2) на множестве действительных чисел: | 1 1 при 0 |
| | Результат конъюнкции предикатов | x=2 0 1 |
| | Результат операции | 1 X=2 1 при 0 |
| | Релейно-контактной схеме | |
| | Релейно-контактной схеме 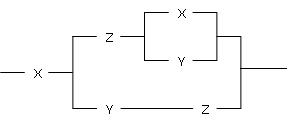 соответствует формула алгебры высказываний: соответствует формула алгебры высказываний: | |
| | Сколько вершин имеет дерево, содержащее N ребер? | N + 1 N N – 1 |
| | Сколько несобственных подмножеств имеет конечное множество, состоящее из n элементов? | n. 2; 1; |
| | Сколько ребер имеет дерево, содержащее n вершин? | n n – 1 |
| |
