Мирзаянов М. Р. Паросочетания и смежные задачи определения и вводные понятия
 Скачать 1.13 Mb.
|
|
Мирзаянов М.Р. Паросочетания и смежные задачи  Мирзаянов М.Р.Паросочетания и смежные задачи §1. Определения и вводные понятияНиже под неориентированным графом, понимаем такой неориентированный граф, в котором нет петель и кратных ребер. Графы будем обозначать символом  , подразумевая, что  – конечное непустое множество вершин, а  – множество неупорядоченных пар из (множество ребер графа). Паросочетанием называется такое множество ребер графа  , что каждая вершина графа инцидентна не более чем одному ребру из  . Например, пустое множество является паросочетанием. Естественно пытаться искать паросочетания, в которых наибольшее количество ребер.Паросочетание называется максимальным, если не существует такого паросочетания  , что .Следует заметить, что в некоторой русскоязычной литературе (например, см. [1]) придерживаются термина «наибольшее паросочетание», термином же «максимальное паросочетание» называют такое паросочетание, которое не является собственным подмножеством никакого другого паросочетания. В соответствии с более употребительной последнее время терминологией, мы будем пользоваться термином «максимальное паросочетание» в смысле количества ребер. 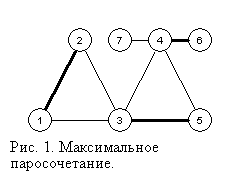 На рис. 1. изображен граф, для которого множество выделенных ребер образует максимальное паросочетание. Неориентированный граф называется двудольным, если множество его вершин можно разбить на два таких подмножества, что не найдется ребра, соединяющей вершины одного подмножества. Известна следующая теорема. Теорема 1 (критерий Кенига). Граф является двудольным тогда и только тогда, когда все циклы в нем имеют четную длину. Ниже часто двудольный граф мы будем обозначать символом  , подчеркивая тем самым, что множество вершин графа разбито на два подмножества  и  .Например, граф изображенный на рис. 1 двудольным не является. Заметим, что задача нахождения максимального паросочетания в двудольных графах решается несколько проще, чем в произвольных графах. Классической формулировкой такой задачи является следующая задача (задача о бракосочетаниях). В ЗАГС поступило несколько заявок о бракосочетаниях. В каждую заявку вписан некоторый юноша и некоторая девушка. В силу прогрессивности современных взглядов один юноша (одна девушка) может содержаться более чем в одной заявки. Так как по закону каждый супруг (супруга) может состоять лишь только в одном союзе, возможно, что не все заявки можно удовлетворить. Какое наибольшее количество заявок можно удовлетворить? Какие это заявки? Если сконструировать граф такой, что юноши образуют вершины одной доли, а девушки – вершины другой, каждую заявку рассматривать как ребро, то задача сводится к поиску максимального паросочетания. Вершины, инцидентные какому-либо ребру паросочетания, называются насыщенными этим паросочетанием. Иногда так будем говорить и о ребрах, то есть насыщенными будем называть ребра паросочетания. В случае если паросочетание насыщает все вершины графа, такое паросочетание будем называть совершенным (или 1-фактором). |