|
|
Мирзаянов М. Р. Паросочетания и смежные задачи определения и вводные понятия
В этом параграфе не только будет приведен метод построения 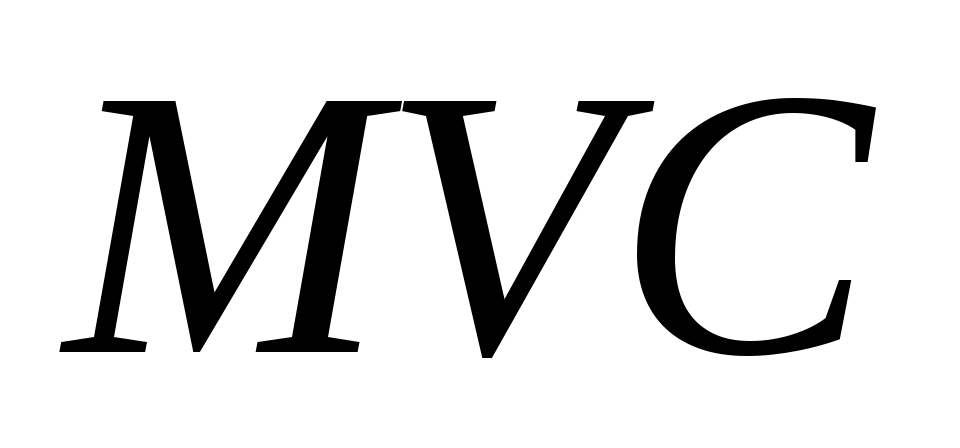 , но и, наконец, доказана теорема 5. , но и, наконец, доказана теорема 5.
Ориентацию ребер двудольного графа 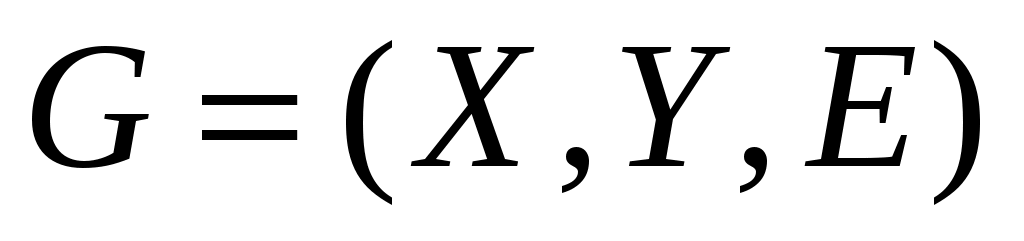 относительно некоторого паросочетания относительно некоторого паросочетания 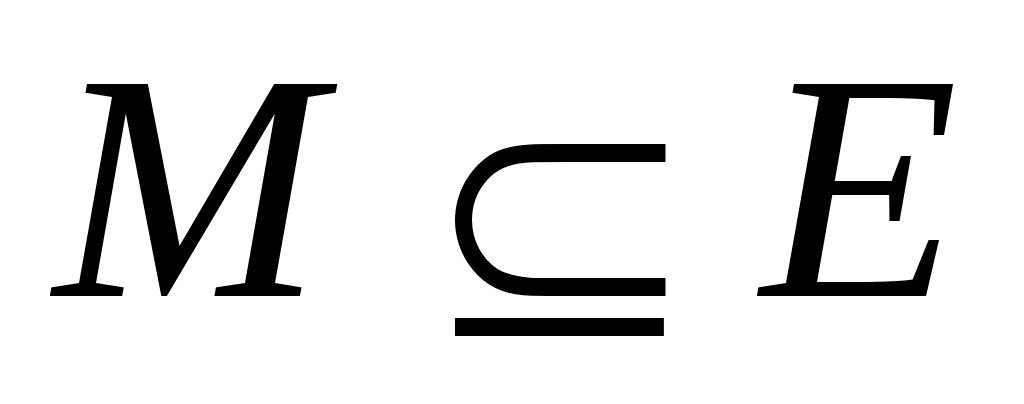 введенную в предыдущем параграфе (см. рис. 6-7) будем называть естественной. введенную в предыдущем параграфе (см. рис. 6-7) будем называть естественной.
Сначала приведем алгоритм построения 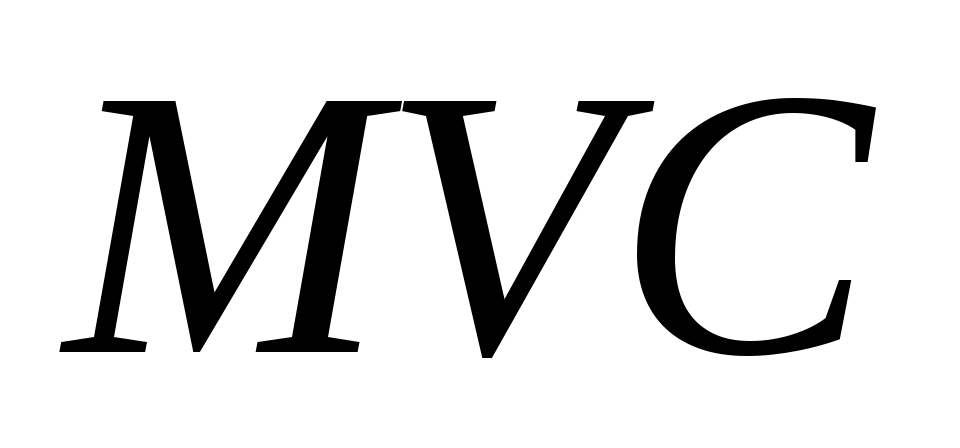 , а затем докажем его корректность. , а затем докажем его корректность.
Алгоритм 5 (общий алгоритм нахождения минимального вершинного покрытия)
Вход: неориентированный двудольный граф 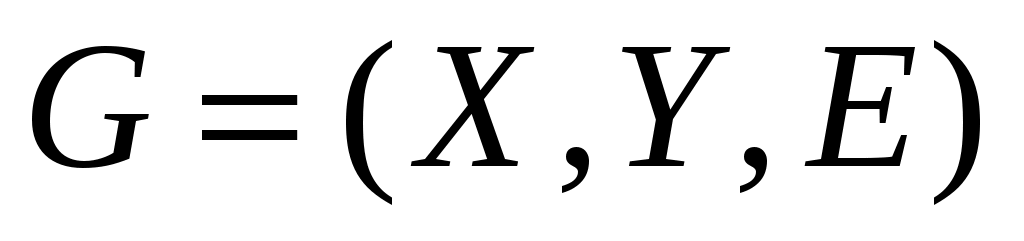
Выход: минимальное вершинное покрытие 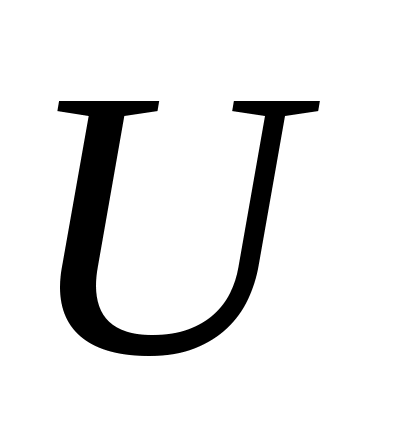
Метод:
function MIN_VERTEX_COVERING(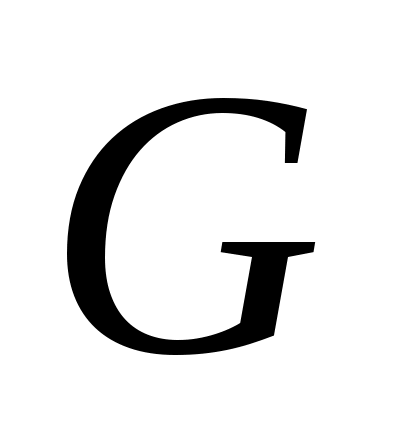 ) )
01  := MAX_MATCHING( := MAX_MATCHING(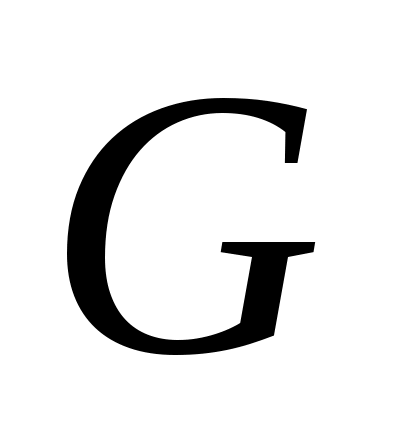 ) )
02 построить 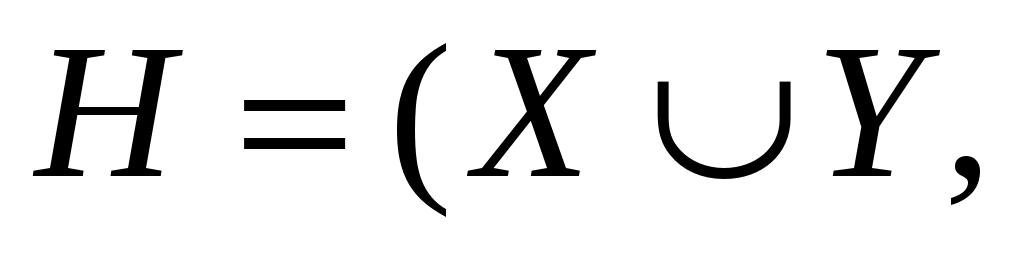 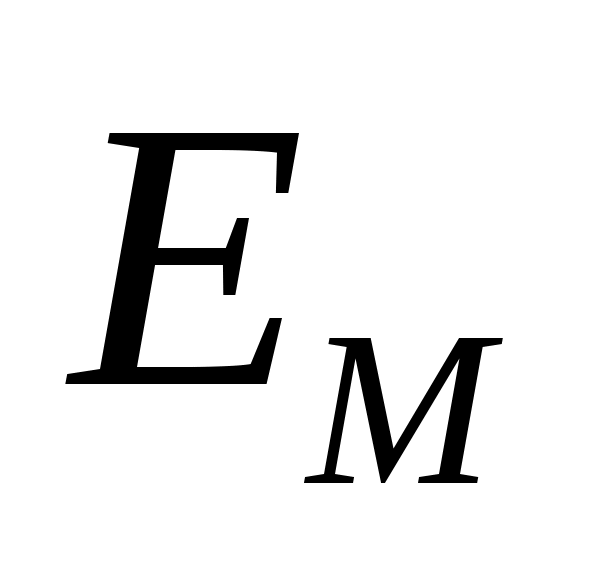 ) – естественную ориентацию ) – естественную ориентацию 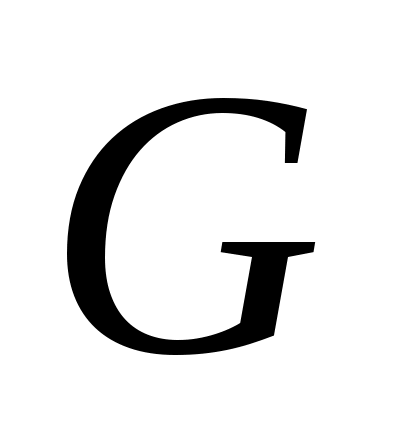
03 найти множество вершин 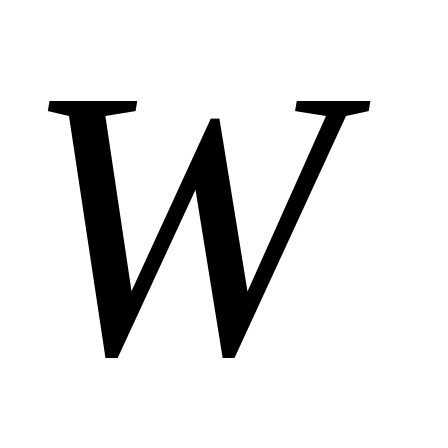 – достижимых – достижимых
из ненасыщенных вершин
множества 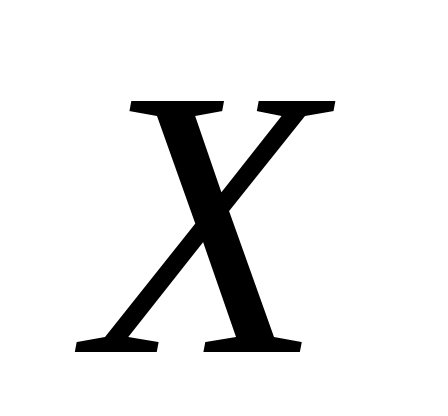 в орграфе в орграфе 
04 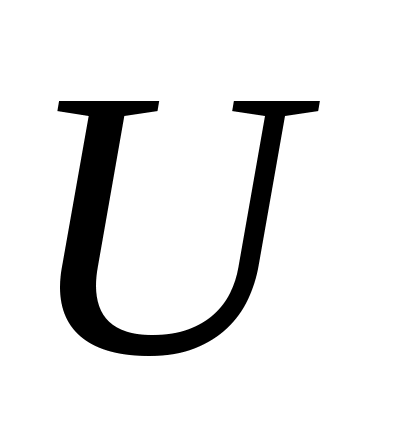 := := 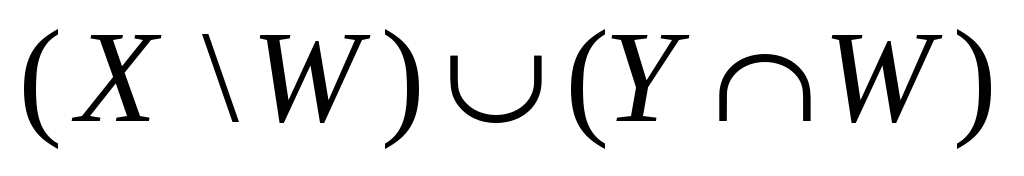
end
|
Заметим, что при реализации этого алгоритма граф  строить совсем не обязательно. Например, можно использовать функцию DFS_MVC( строить совсем не обязательно. Например, можно использовать функцию DFS_MVC( ), имеющую минимальное различие с функцией TRY_KHUN( ), имеющую минимальное различие с функцией TRY_KHUN( ). ).
Алгоритм 6 (детальный алгоритм нахождения минимального
вершинного покрытия)
Вход: неориентированный двудольный граф 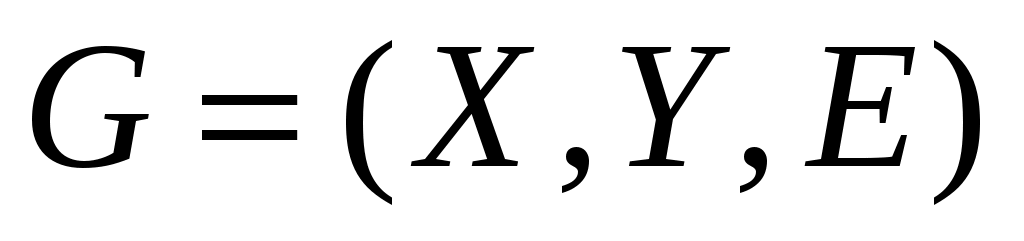
Выход: минимальное вершинное покрытие 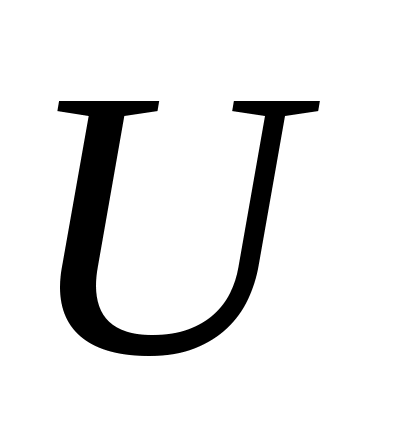
Метод:
function MIN_VERTEX _COVERING(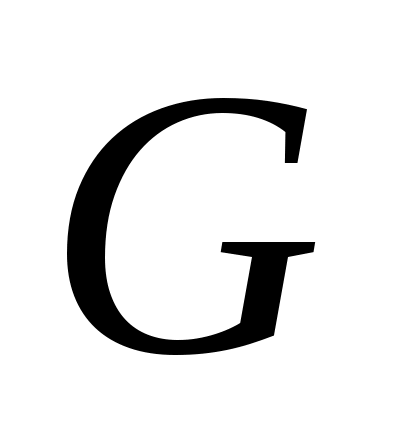 ) )
01  := MAX_MATCHING( := MAX_MATCHING(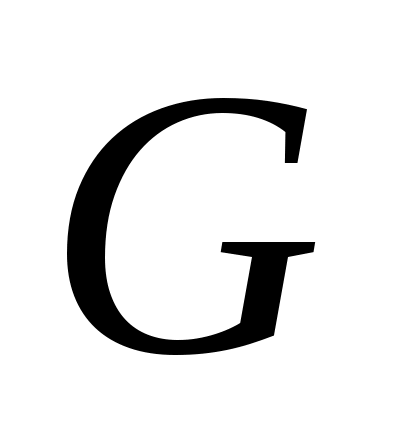 ) )
02 Fill(used_x, FALSE)
03 Fill(used_y, FALSE)
04 for 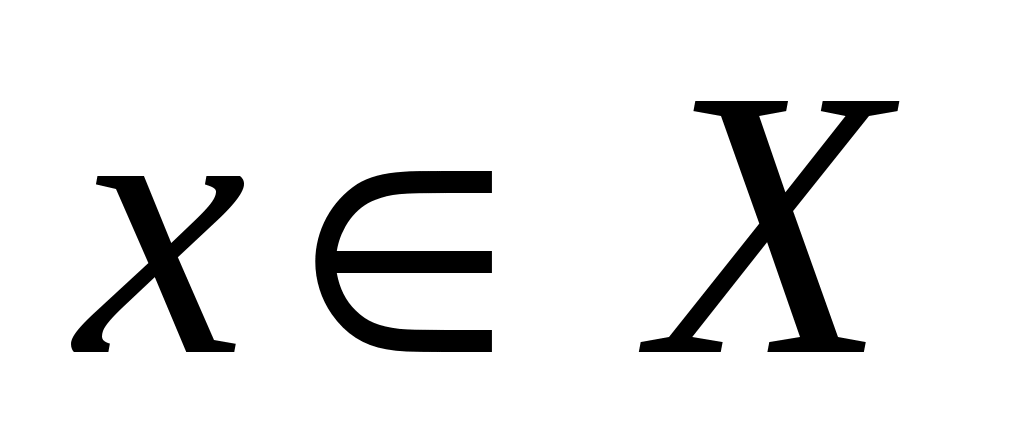 do do
05 if  не насыщенна не насыщенна  then then
06 DFS_MVC( ) )
07 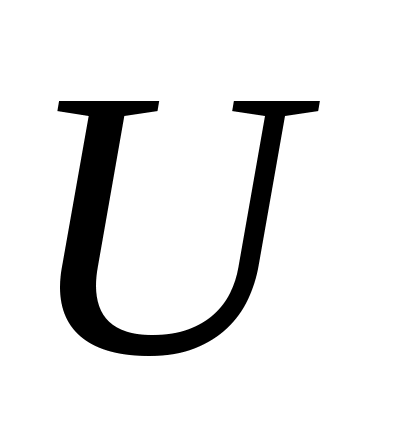 := (!used_x) := (!used_x)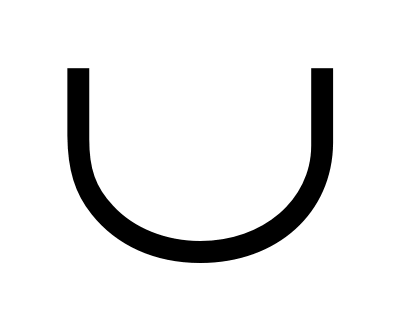 used_y used_y
end
|
Функция DFS_MVC( ) выглядит следующим образом. ) выглядит следующим образом.
Функция DFS_MVC( ). ).
Вход: вершина  множества множества 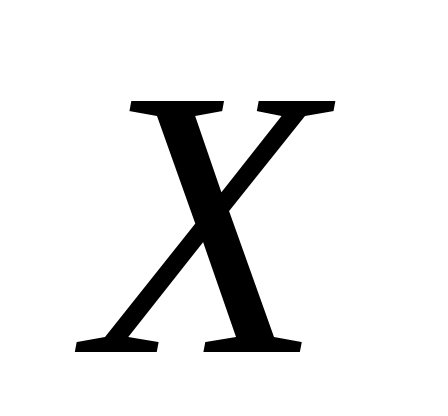
Выход: пустой (результаты сохраняются в used_x, used_y)
Глобальные переменные: двудольный граф 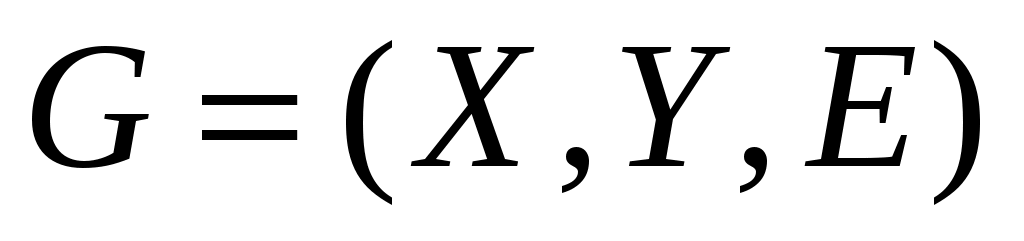 , паросочетание , паросочетание  , булевские массивы used_x, used_y проиндексиванные элементами множеств , булевские массивы used_x, used_y проиндексиванные элементами множеств 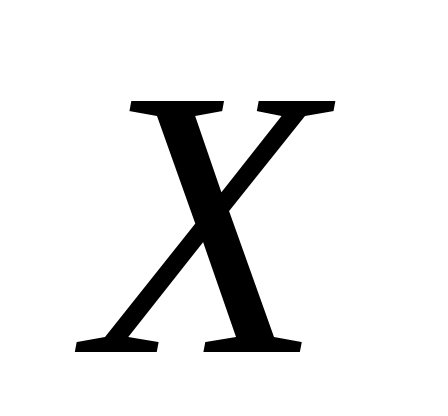 , , 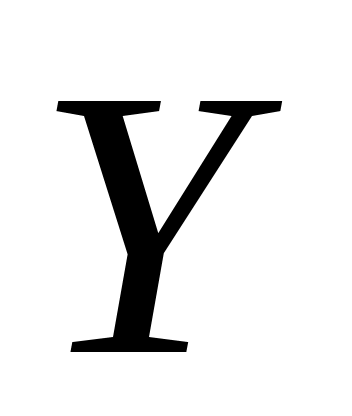 соответственно. соответственно.
Метод:
function DFS_MVC( ) )
01 if used_x[ ] then ] then
02 return
03 used_x[ ] := TRUE ] := TRUE
04 for 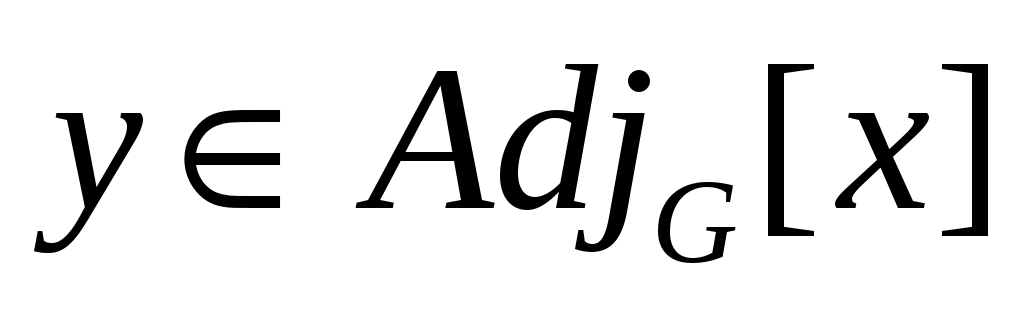 do do
05 used_y[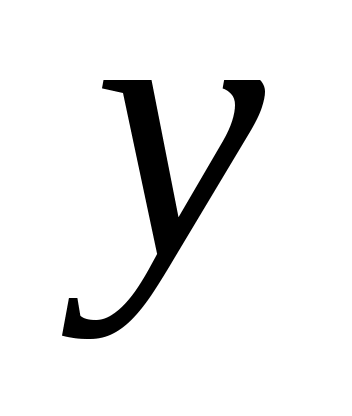 ] := TRUE ] := TRUE
06 if 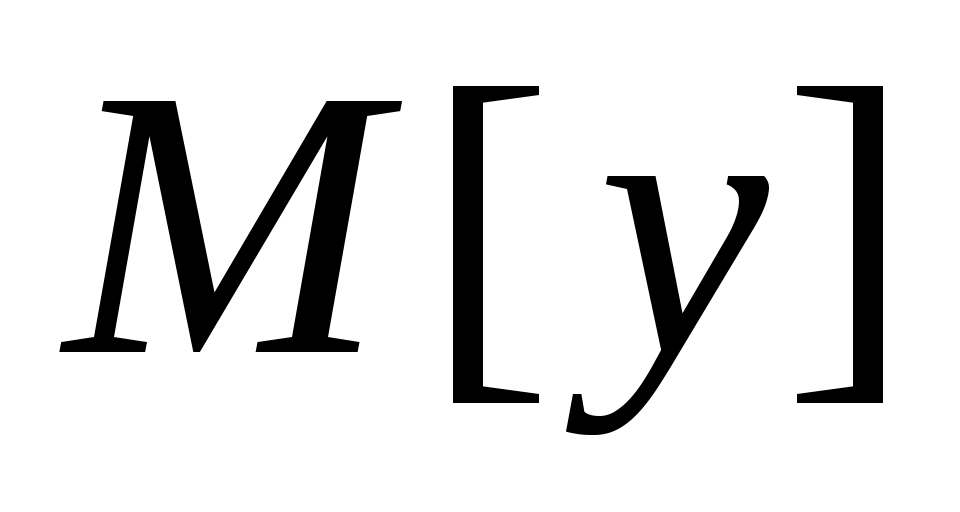 не равно не равно 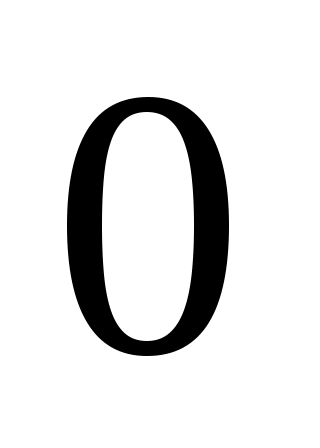 then then
07 DFS_MVC(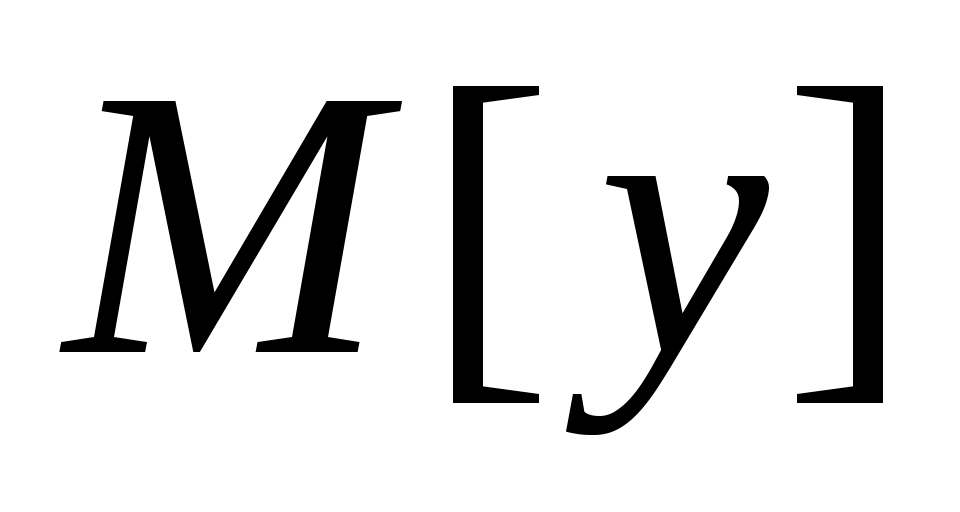 ) )
end
|
В строке 06 алгоритма 6 символом !used_x обозначается дополнение множества used_x до 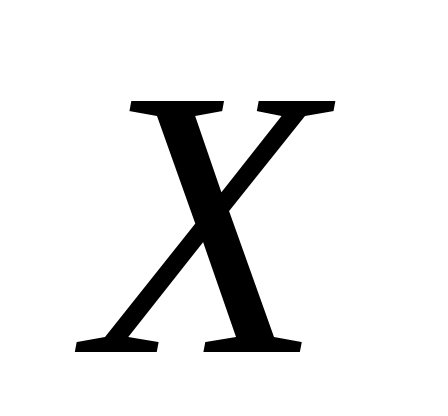 . Так как алгоритм 6 является лишь детальным изложением алгоритма 5, то достаточно доказать только корректность алгоритма 5. . Так как алгоритм 6 является лишь детальным изложением алгоритма 5, то достаточно доказать только корректность алгоритма 5.
Лемма 2. В произвольном графе 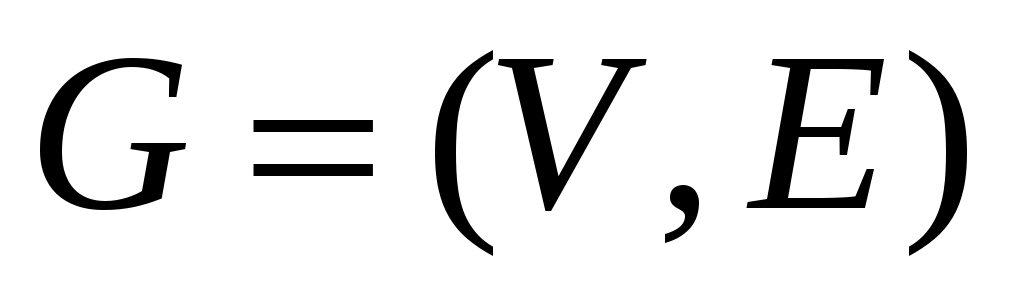 верно неравенство: верно неравенство:
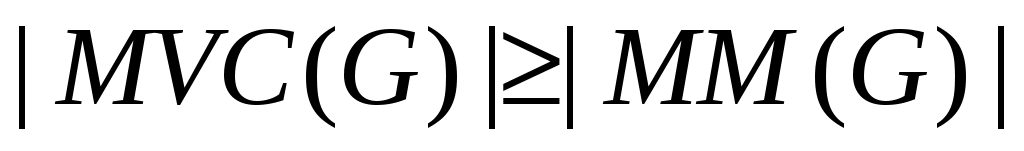 . .
Доказательство. В самом деле, каждое ребро максимального паросочетания инцидентно хотя бы одной вершине вершинного покрытие, но все вершины инцидентные паросочетанию – различны. 
Теорема 8.Алгоритм 5 – корректен.
Доказательство. Докажем, что найденное множество 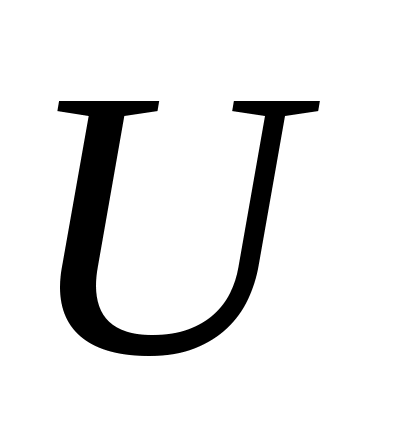 в самом деле образует вершинное покрытие. Предположим существование такого ребра в самом деле образует вершинное покрытие. Предположим существование такого ребра 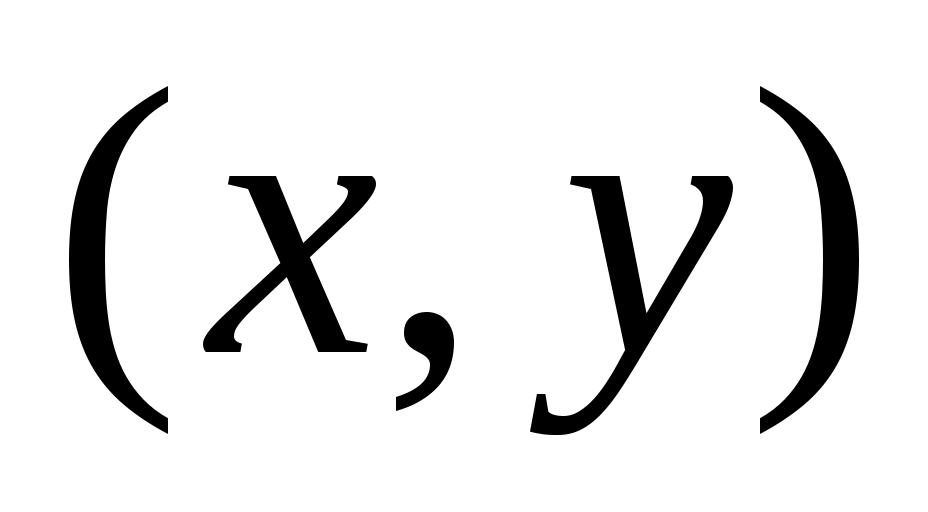 , что вершина , что вершина  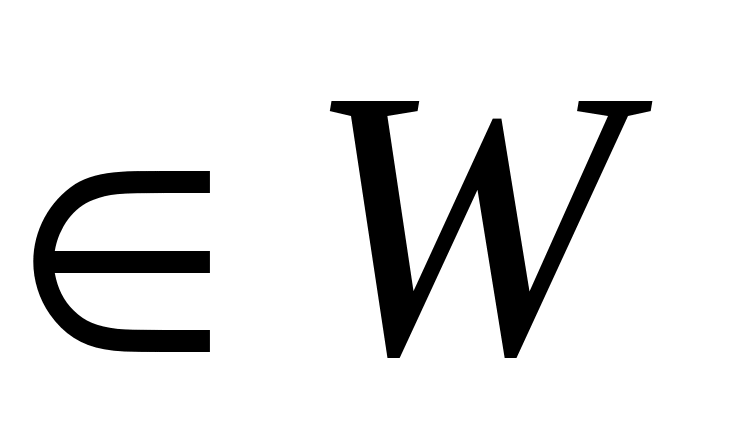 , а , а 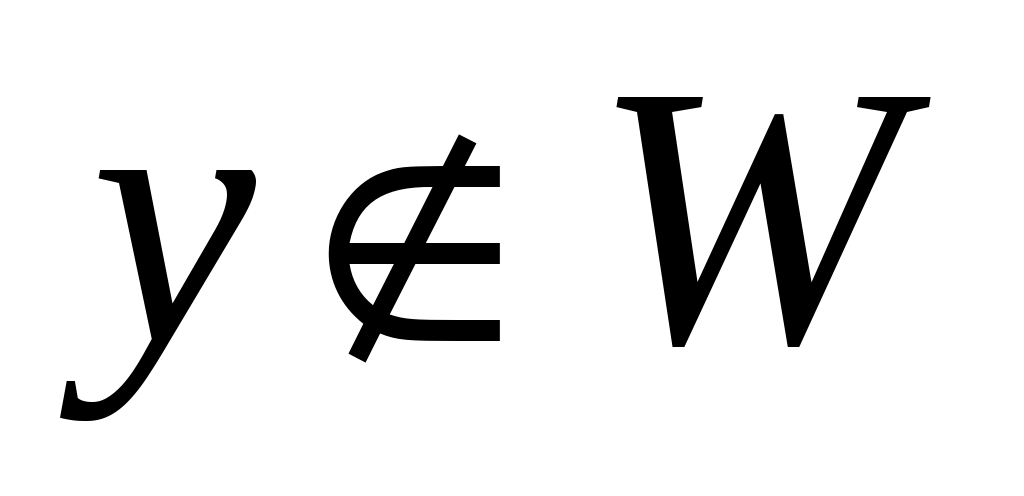 . Возможен один из двух случаев: . Возможен один из двух случаев: 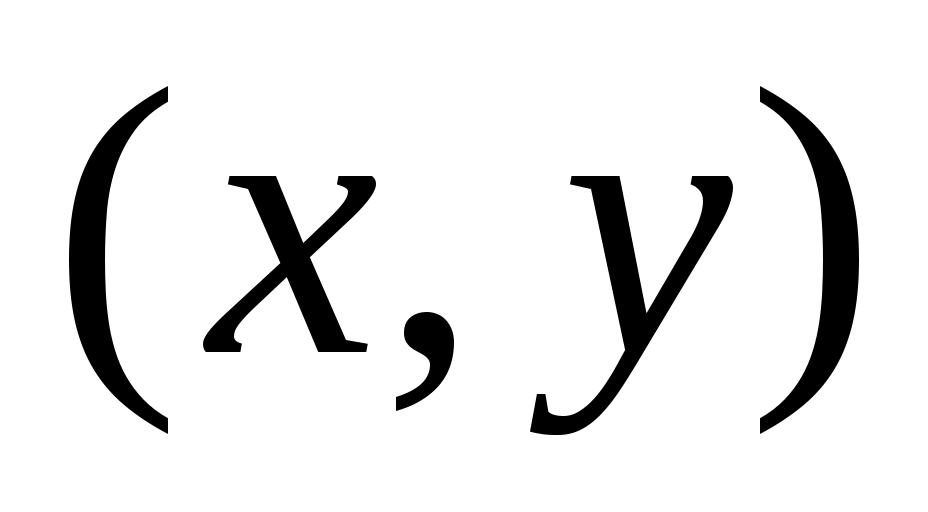   и и 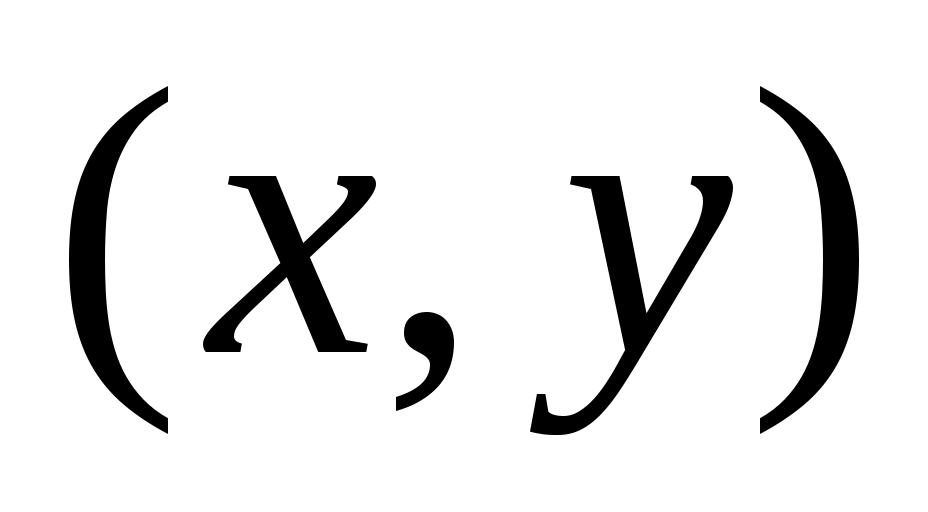 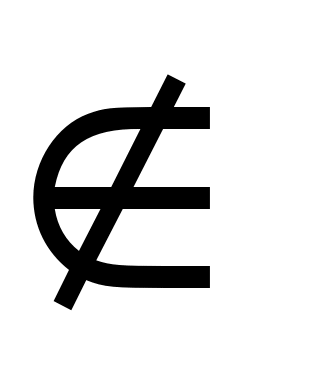  . .
Пусть 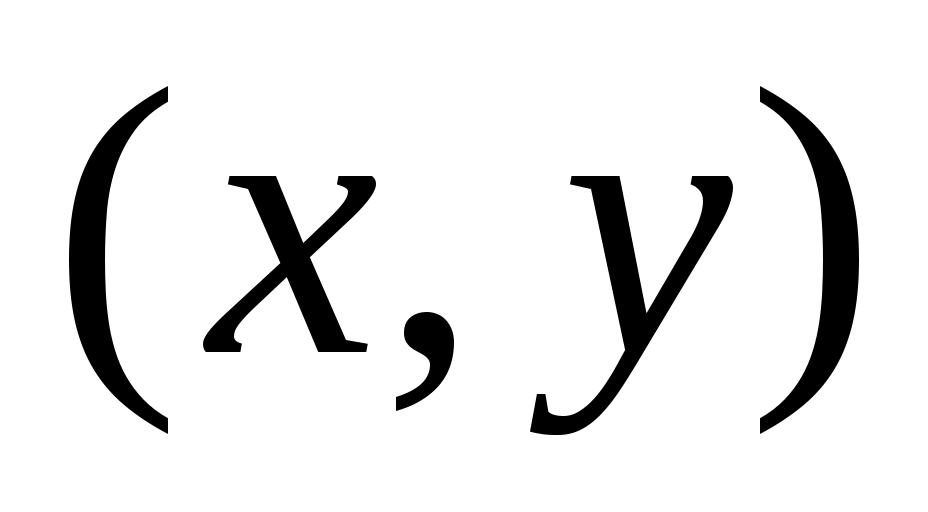   . В этом случае вершина . В этом случае вершина  насыщена паросочетанием и попасть в насыщена паросочетанием и попасть в 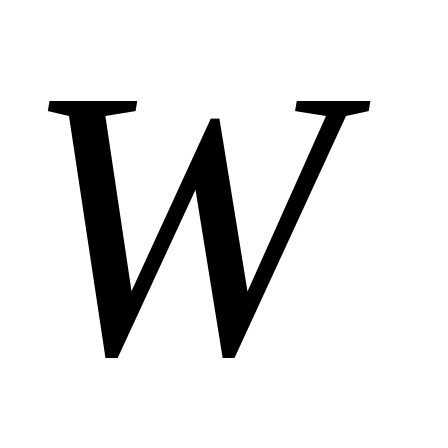 она может лишь в случае существования некоторой цепи она может лишь в случае существования некоторой цепи 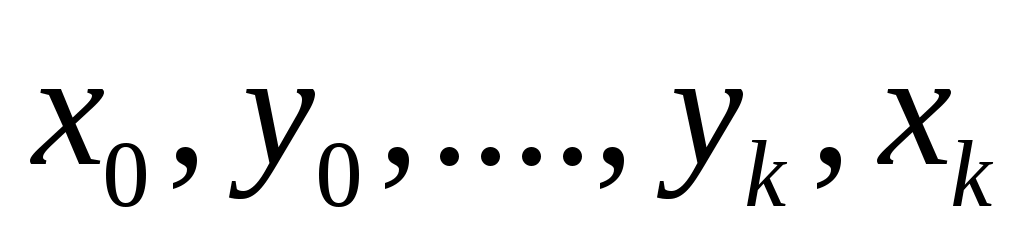 в графе в графе  , где , где 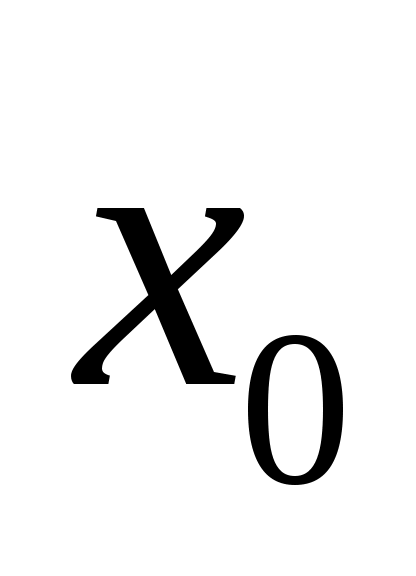 – ненасыщенная вершина, а – ненасыщенная вершина, а 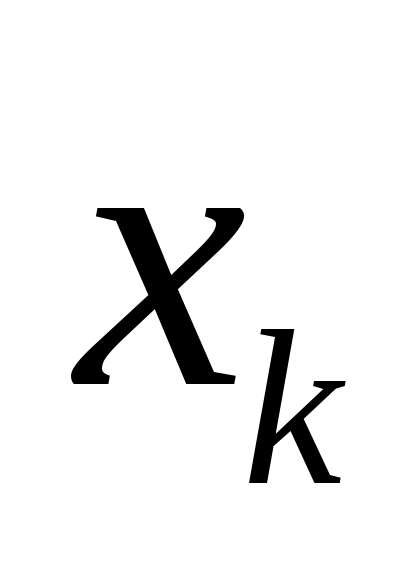 = = . Так как переходить из доли . Так как переходить из доли 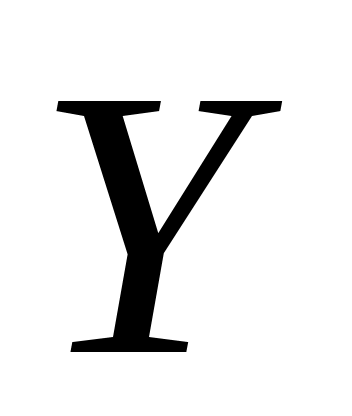 в в 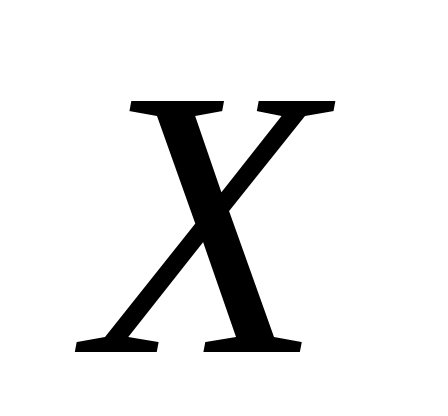 можно только по ребрам из можно только по ребрам из  , получаем, что , получаем, что 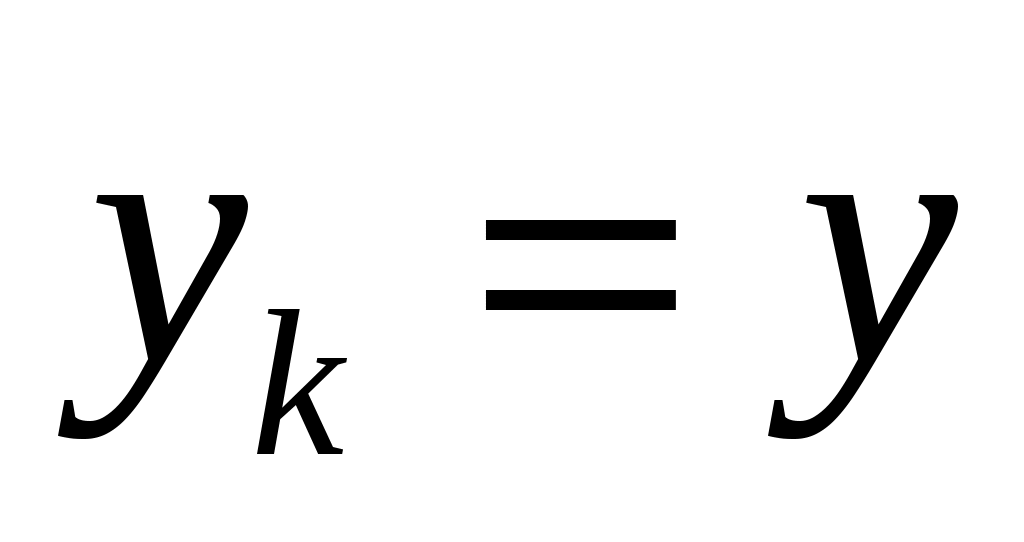 , то есть вершина , то есть вершина  . Противоречие. . Противоречие.
Предположим 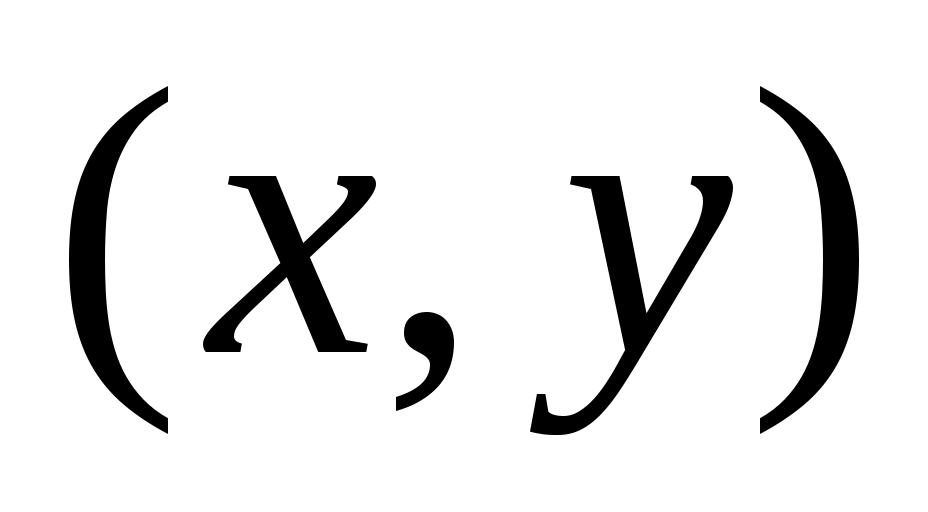 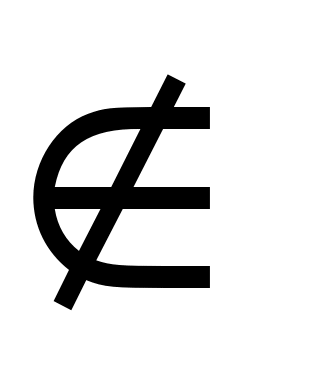  . В этом случае из . В этом случае из 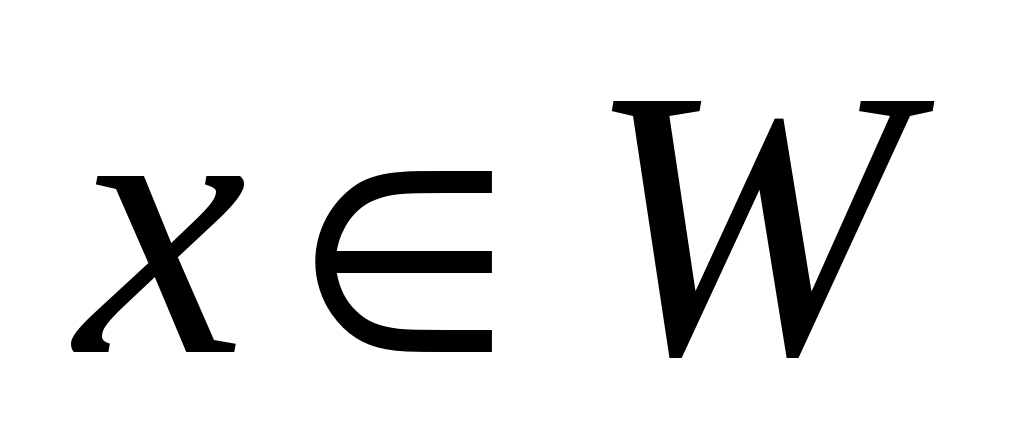 немедленно следует немедленно следует  . Получаем противоречие. . Получаем противоречие.
Итак, множество 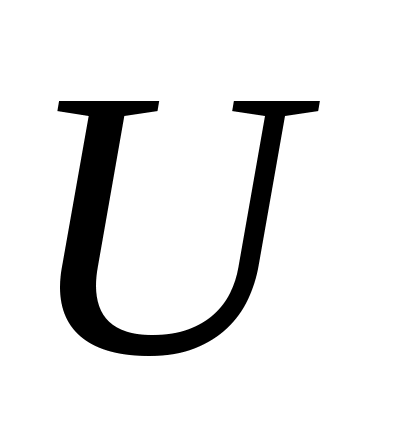 в самом деле является вершинным покрытием. в самом деле является вершинным покрытием.
Покажем его минимальность. В силу леммы 2 достаточно доказать, что 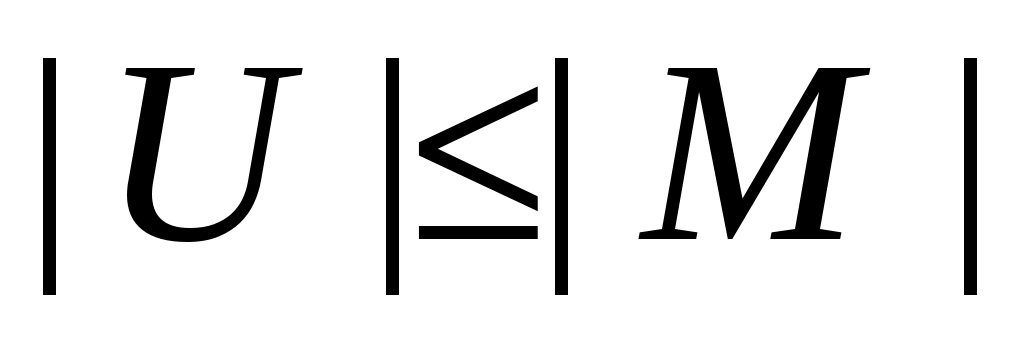 . Очевидно, каждое ребро из множества . Очевидно, каждое ребро из множества  инцидентно не более чем одной вершине из множества инцидентно не более чем одной вершине из множества 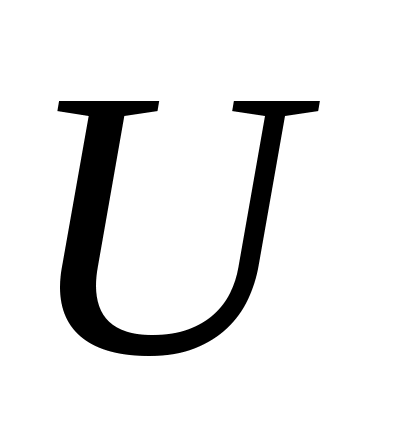 . Покажем, что все вершины из . Покажем, что все вершины из 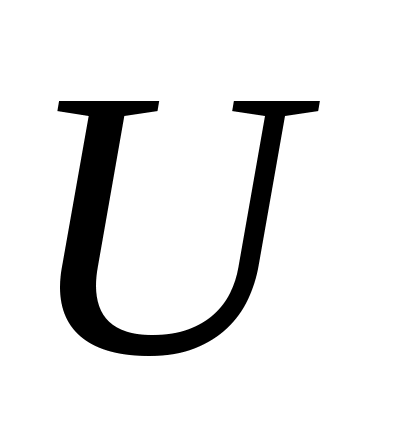 инцидентны какому-то ребру из паросочетания инцидентны какому-то ребру из паросочетания  . Предположим противное, то есть допустим, что в множестве . Предположим противное, то есть допустим, что в множестве 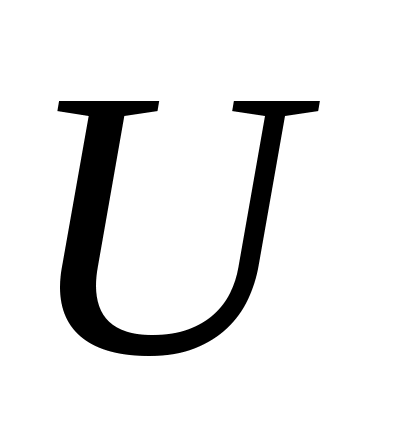 существует ненасыщенная вершина. Очевидно, что эту вершина не принадлежит доли существует ненасыщенная вершина. Очевидно, что эту вершина не принадлежит доли 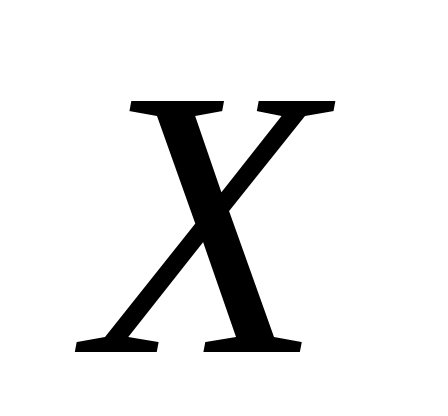 (так как все ненасыщенные вершины доли (так как все ненасыщенные вершины доли 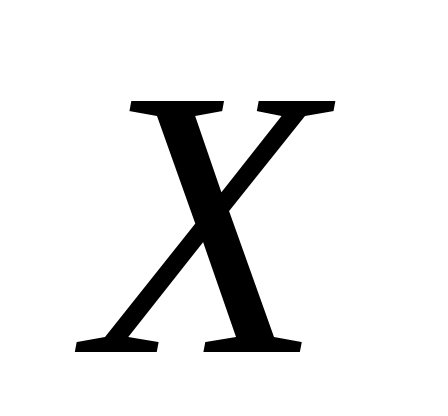 достижимы из себя и, следовательно, принадлежат достижимы из себя и, следовательно, принадлежат 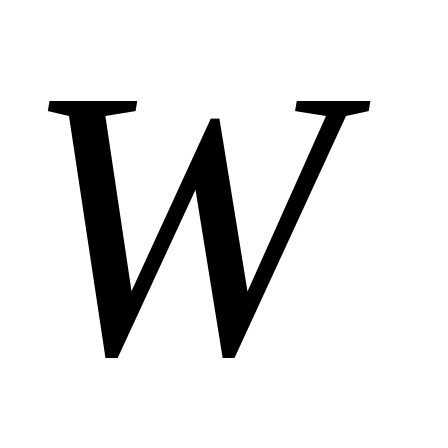 ). Доли ). Доли 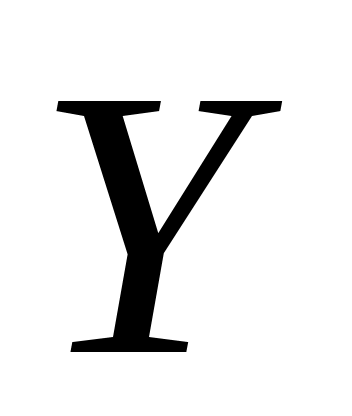 эта вершина принадлежать тоже не может, так как это обозначало бы наличие в эта вершина принадлежать тоже не может, так как это обозначало бы наличие в   -увеличивающей цепи, заканчивающейся в этой вершине. Таким образом, -увеличивающей цепи, заканчивающейся в этой вершине. Таким образом, 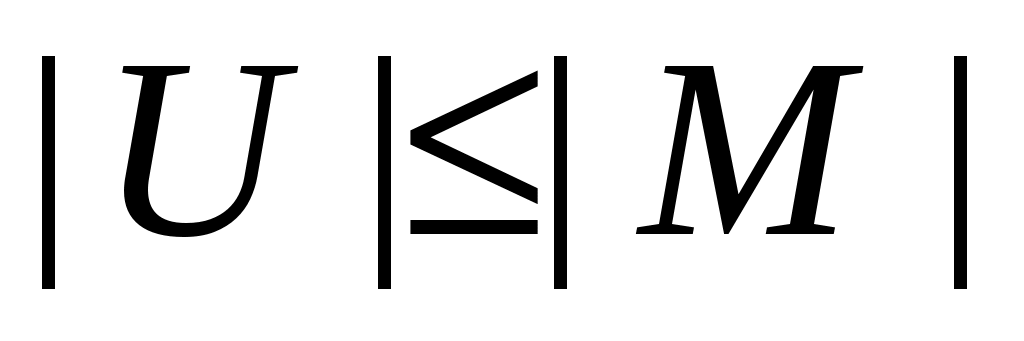 . По лемме 2 получаем, что . По лемме 2 получаем, что 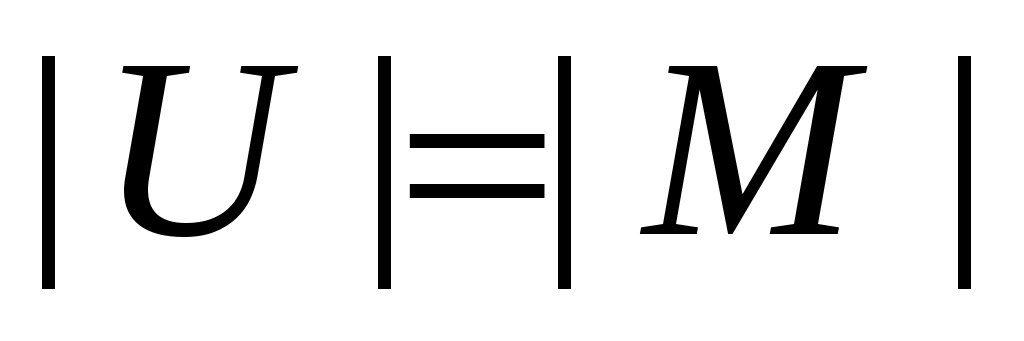 и и 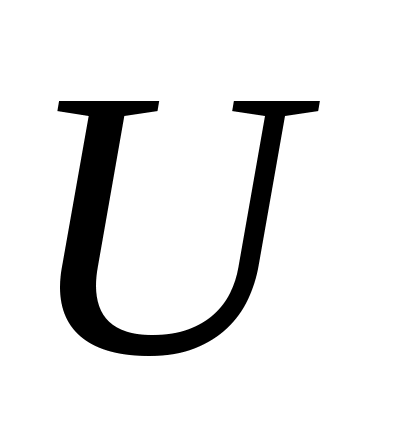 – минимальное вершинное покрытие. – минимальное вершинное покрытие.
Заметим, что в ходе доказательства теоремы 8 доказана теорема 5.
|
|
|
 Скачать 1.13 Mb.
Скачать 1.13 Mb.