§4. Эквивалентность задач: MM и MVC для двудольных графов
Теорема 4 (матричная теорема Кенига). Наименьшее количество вертикальных и/или горизонтальных линий, содержащее все единицы некоторой 0-1 прямоугольной матрицы равно наибольшему количеству попарно независимых единиц.
В теореме 4 подразумевается, что две единицы 0-1 прямоугольной матрицы независимы, если они не находятся на одной вертикали и/или горизонтали.
Теорему 4 мы докажем чуть позже.
Поставим в соответствие прямоугольной матрице двудольный граф, вершинами первой доли которого являются строки данной матрицы, а вершинами второй – столбцы. Каждая единица матрицы порождает одно ребро в графе, концами которого являются строка и столбец, на пересечении которых она расположена. Таким образом, наименьшее количество вертикальных и горизонтальных линий, содержащих все единицы матрицы, соответствует наименьшему вершинному покрытию в построенном графе. В свою очередь наибольшее количество попарно независимых единиц соответствует максимальному паросочетанию. Переформулируем теорему в терминах теории графов.
Теорема 5. В произвольном двудольном графе мощность минимального вершинного покрытия равна мощности наибольшего паросочетания.
Доказательство теоремы 5 будет приведено позже.
Представим, что нам известно не только доказательство теоремы 5, но и способ перехода от минимального вершинного покрытия к максимальному паросочетанию (и наоборот). На рис. 5 показана эквивалентность всех четырех основных задач.
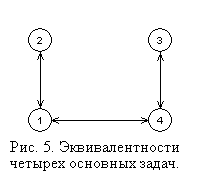
Переход 1-2 осуществляется в силу теоремы 3, 3-4 – в силу теоремы 2, 1-4 – в силу теоремы 5.
§5. Построение максимального паросочетания в двудольном графе
Рассмотрим некоторый граф 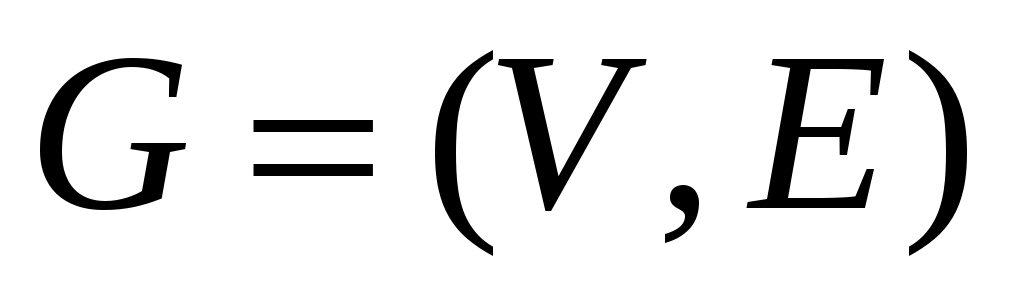 . Пусть . Пусть 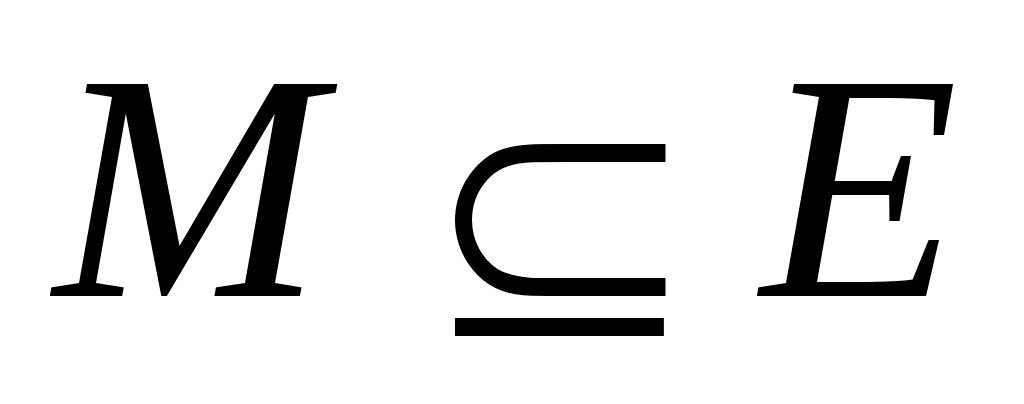 – паросочетание в нем. – паросочетание в нем.
Цепью будем называть последовательность ребер 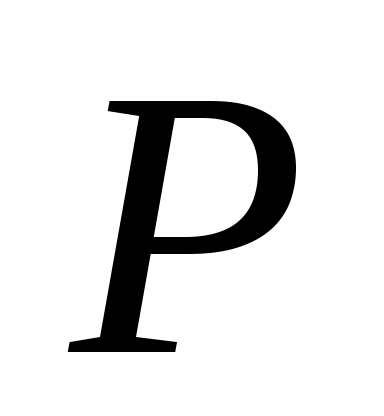 вида вида 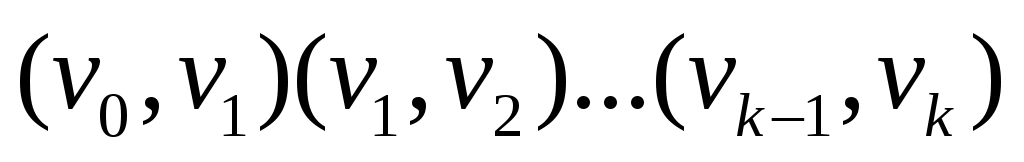 . Число . Число 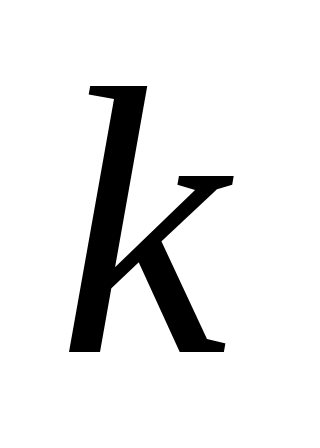 называется длиной цепи называется длиной цепи 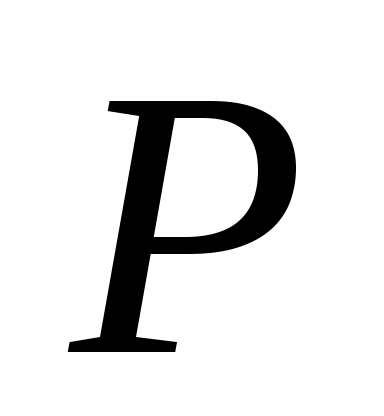 . Иногда цепи будем записывать в сжатом виде, например, . Иногда цепи будем записывать в сжатом виде, например, 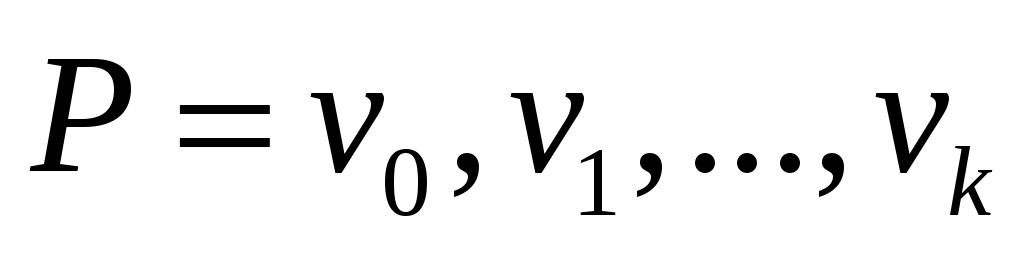 . .
Назовем цепь 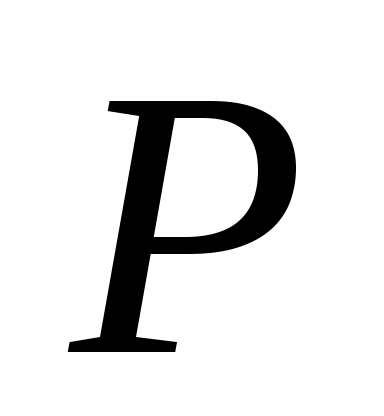 чередующейся относительно паросочетания чередующейся относительно паросочетания  (или (или  -чередующейся), если ребра в последовательности поочередно принадлежат -чередующейся), если ребра в последовательности поочередно принадлежат  и и 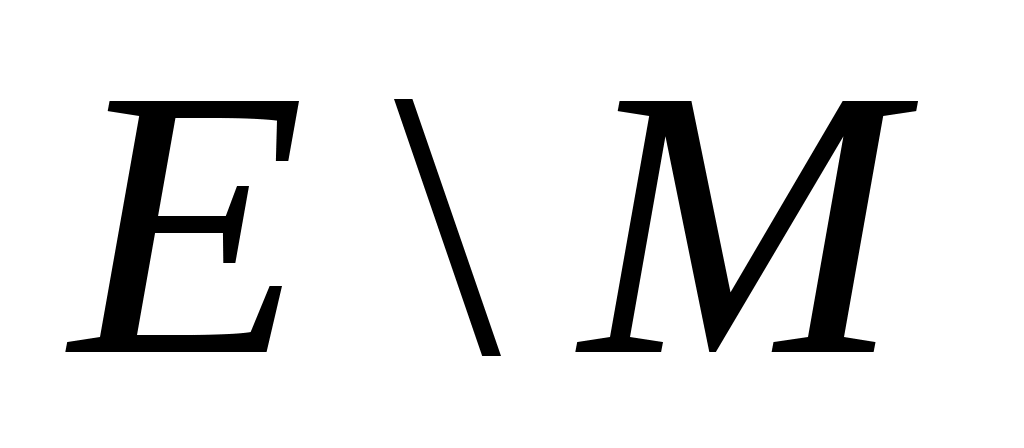 . .
 -чередующаяся цепь называется увеличивающей относительно паросочетания -чередующаяся цепь называется увеличивающей относительно паросочетания  , если ее начальная и конечная вершины ненасыщенны. , если ее начальная и конечная вершины ненасыщенны.
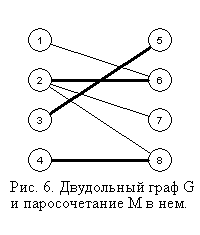
На рис. 6 изображен некоторый двудольный граф 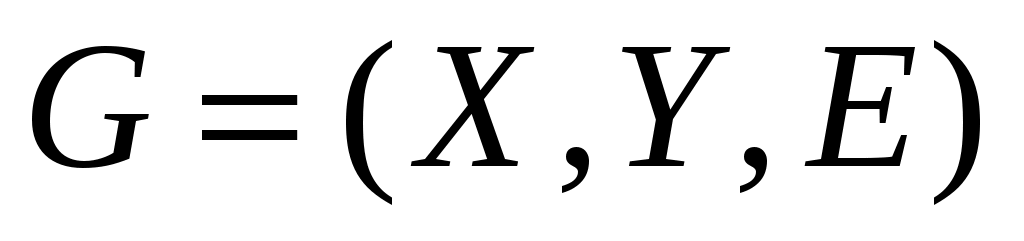 , выделенные ребра обозначают ребра паросочетания , выделенные ребра обозначают ребра паросочетания  . Заметим, что для введеных определений граф . Заметим, что для введеных определений граф 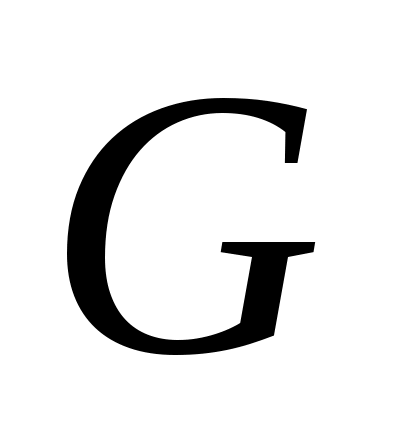 не обязательно должен быть двудольным. Перечислим некоторые не обязательно должен быть двудольным. Перечислим некоторые  -чередующиеся цепи в нем: -чередующиеся цепи в нем: 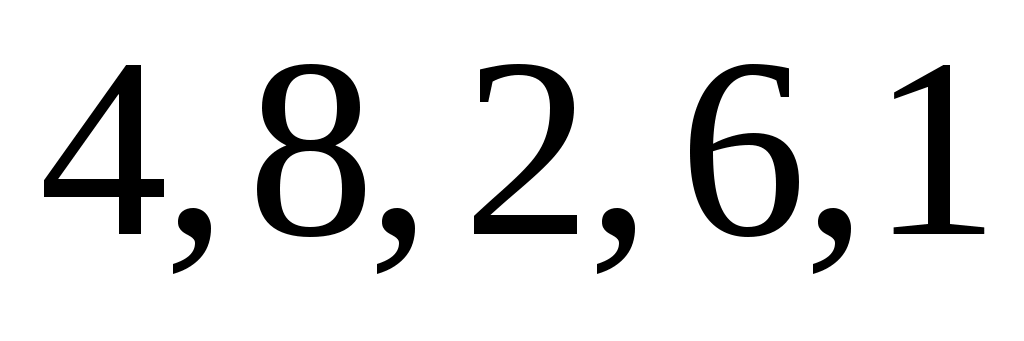 ; ; 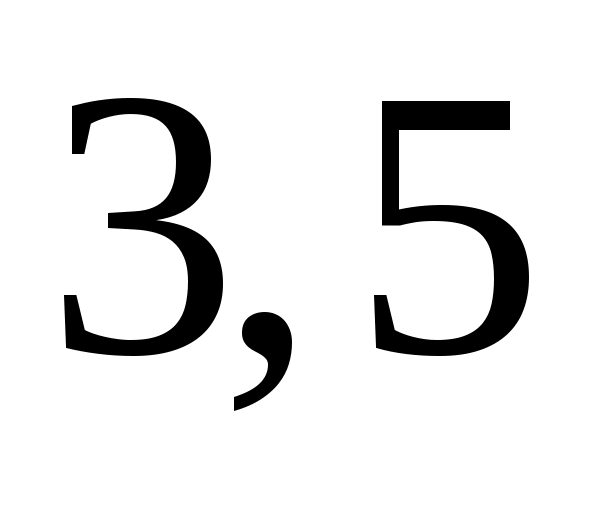 ; ; 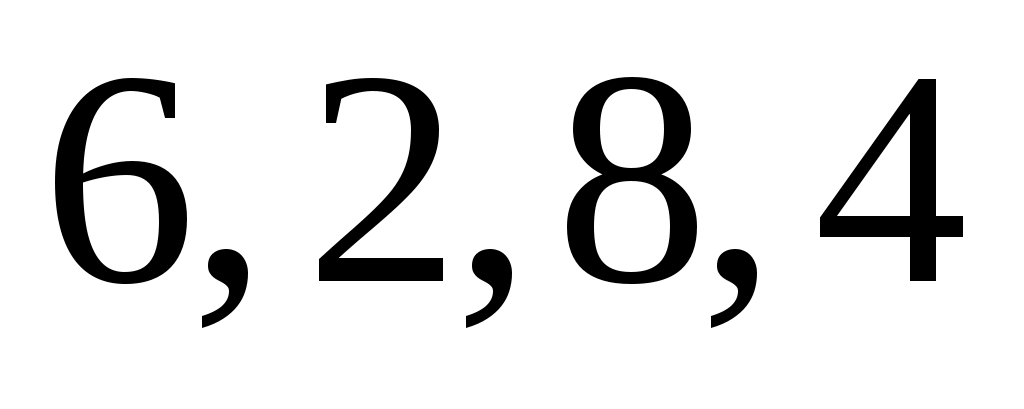 ; ; 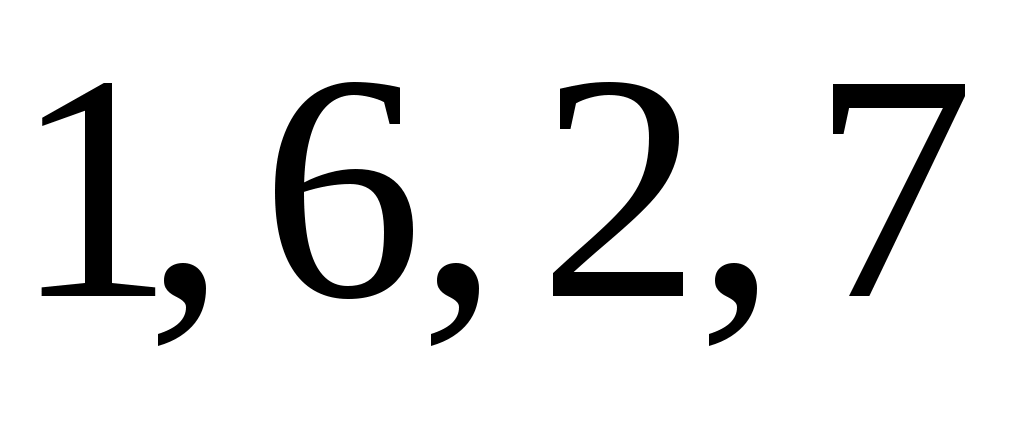 . Заметим, что последняя из них является . Заметим, что последняя из них является  -увеличивающей. -увеличивающей.
Символом  будем пользоваться для обозначения бинарного оператора симметрической разности, т.е. если будем пользоваться для обозначения бинарного оператора симметрической разности, т.е. если 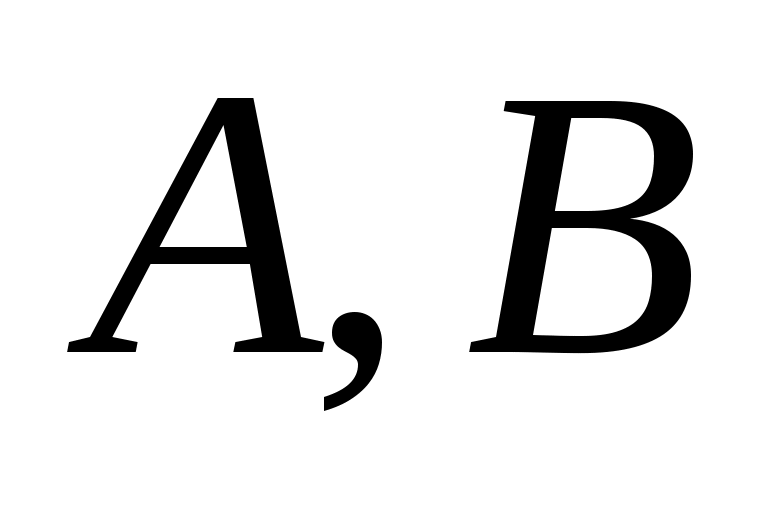 – некоторые множества, то – некоторые множества, то
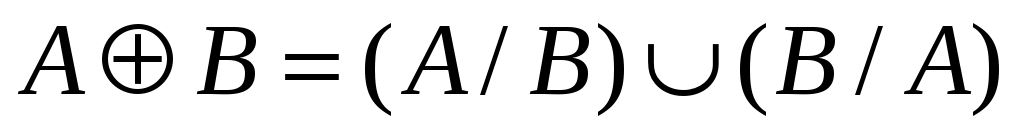 . .
Лемма 1. Пусть 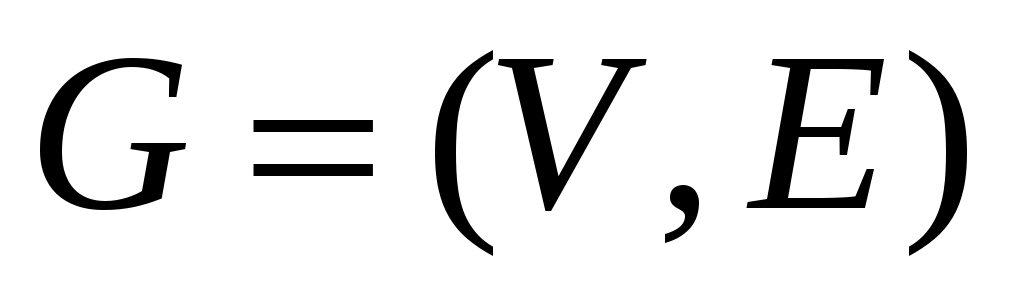 – произвольный неориентированный граф и – произвольный неориентированный граф и 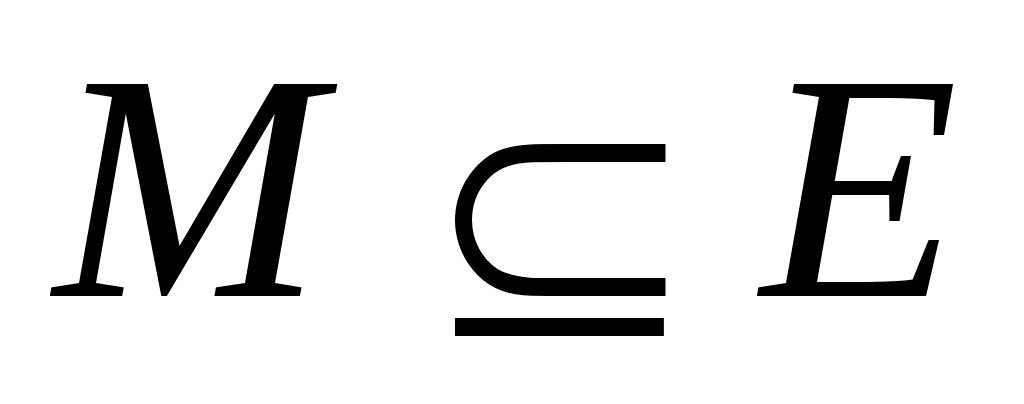 – паросочетание в нем. Тогда если существует – паросочетание в нем. Тогда если существует  -увеличивающая цепь -увеличивающая цепь 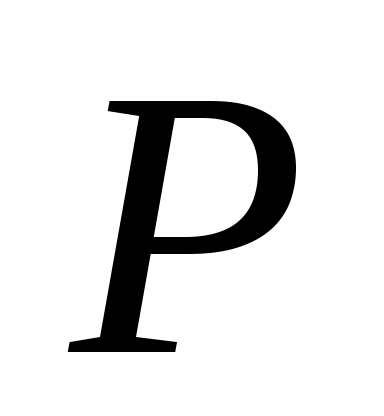 , то , то  – паросочетание в – паросочетание в 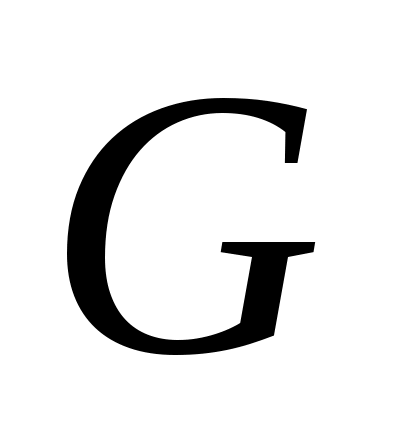 и и 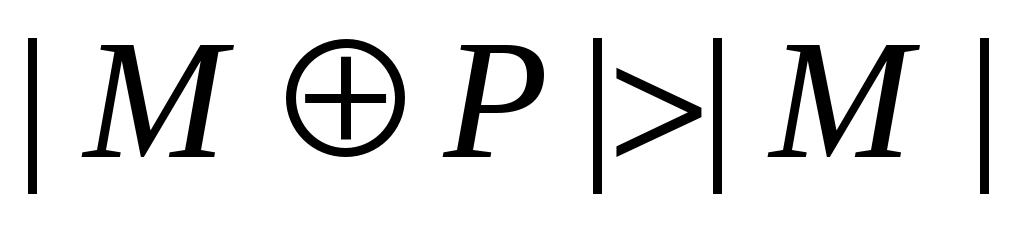 . .
Доказательство. В самом деле, так как 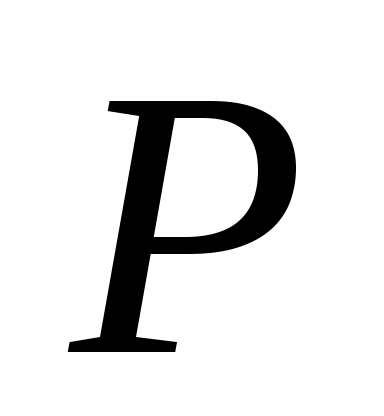 является является  -увеличивающей цепью, то ребра -увеличивающей цепью, то ребра 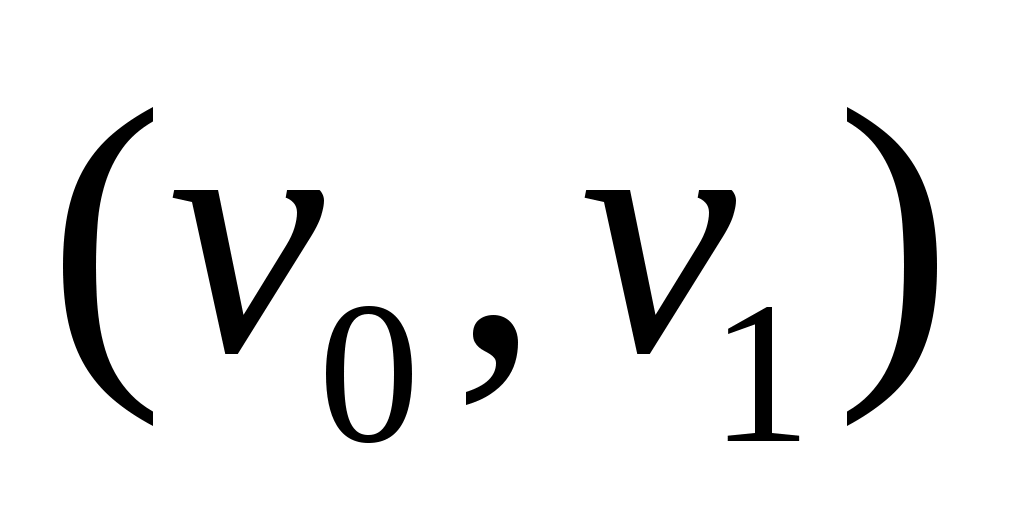 и и 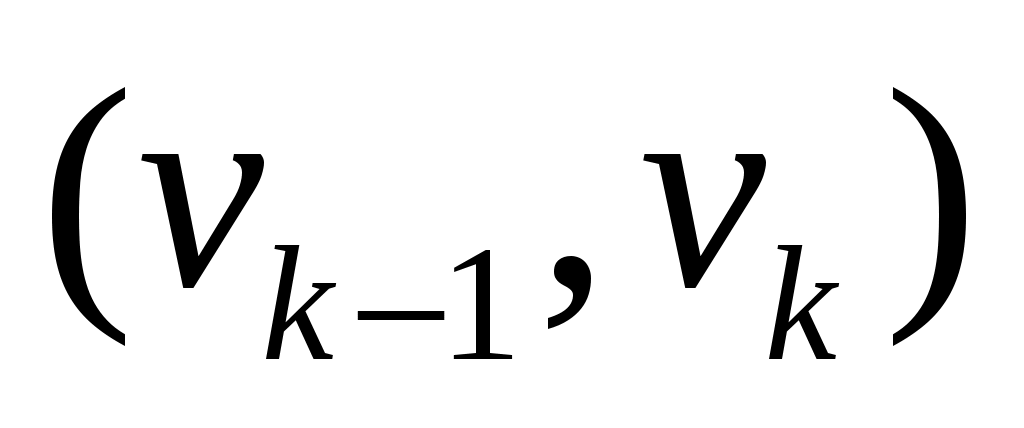 не принадлежат не принадлежат  . Следовательно, . Следовательно, 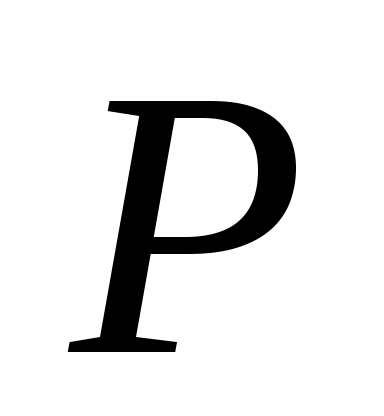 имеет нечетную длину. Таким образом, имеет нечетную длину. Таким образом,  содержит на одно ребро больше, чем содержит на одно ребро больше, чем  . .
Покажем, что  является паросочетанием. Предположим, что некоторая вершина является паросочетанием. Предположим, что некоторая вершина 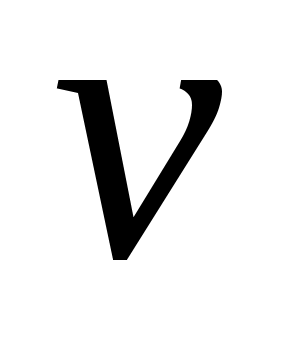 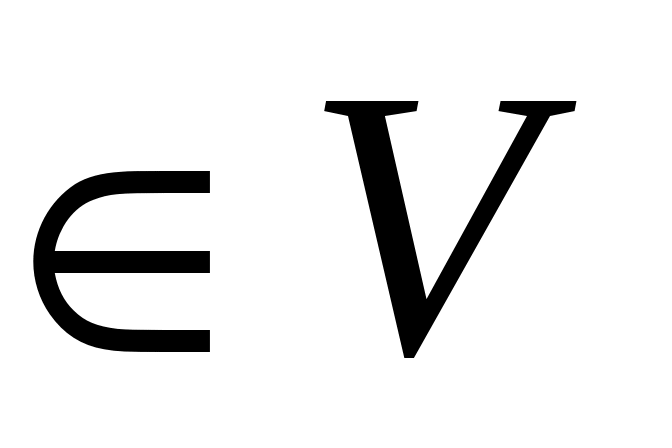 инцидентна более чем одному ребру из инцидентна более чем одному ребру из  . Так как вершины . Так как вершины 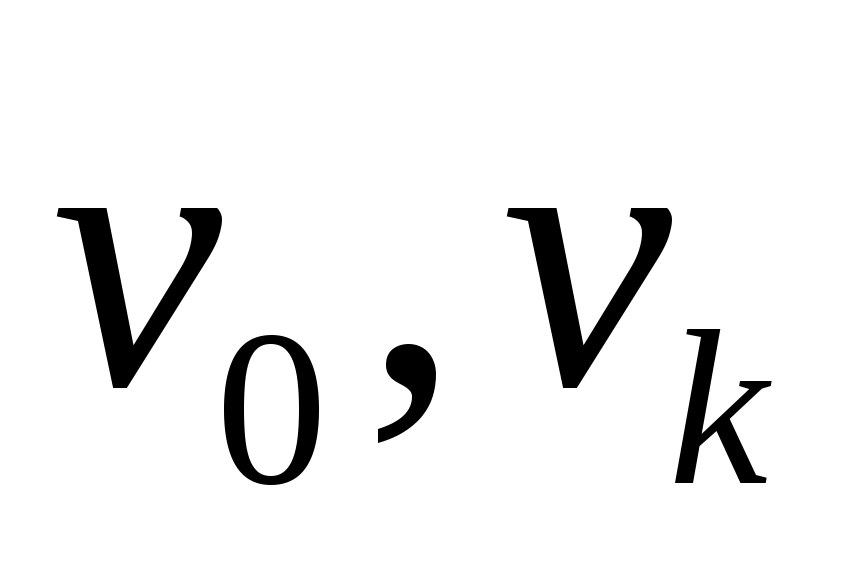 – ненасыщенны паросочетанием – ненасыщенны паросочетанием  , то , то 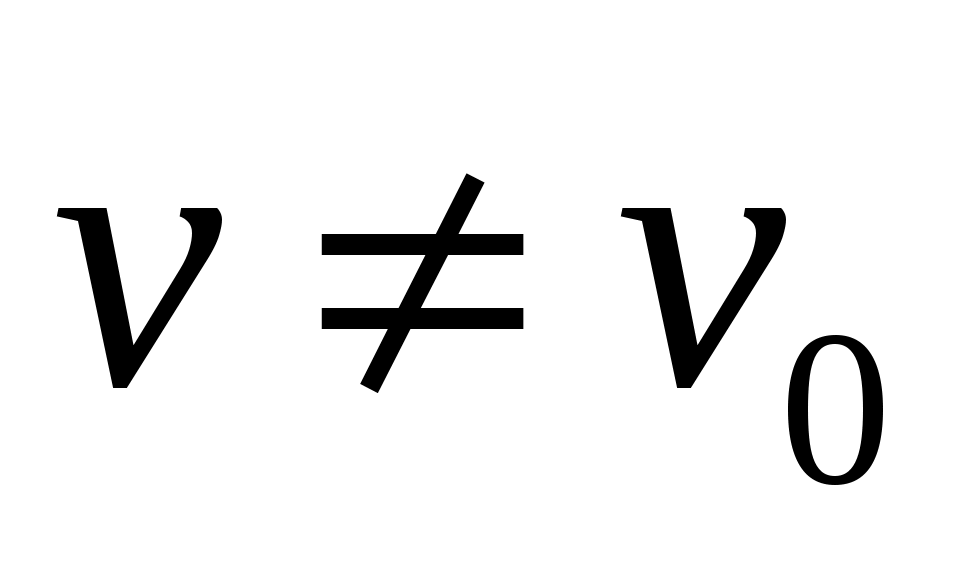 и и 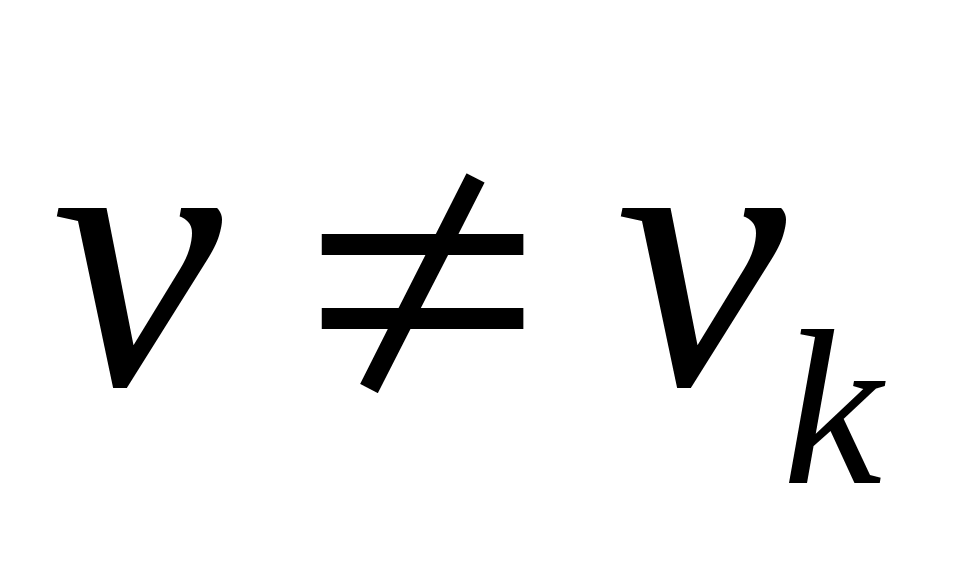 . Значит вершина . Значит вершина 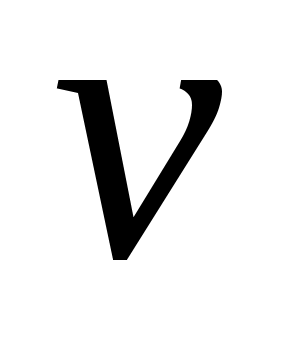 является внутренней вершиной цепи является внутренней вершиной цепи 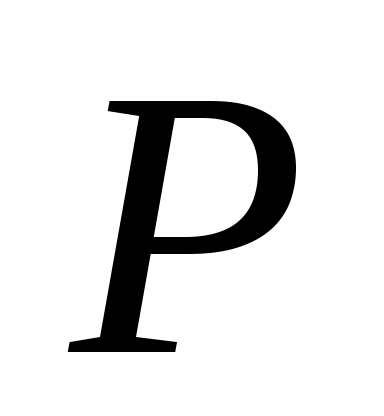 . Из тех ребер множества . Из тех ребер множества  , которые инцидентны , которые инцидентны 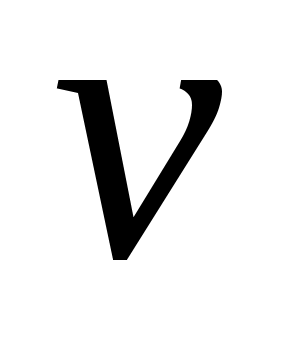 ровно одно принадлежит ровно одно принадлежит 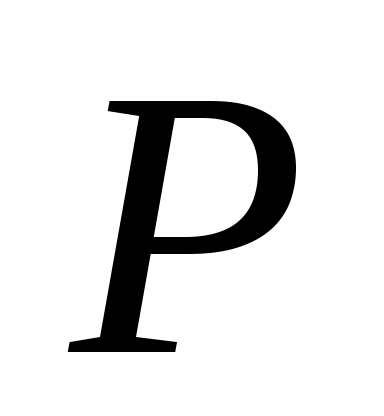 , и не менее одного принадлежит , и не менее одного принадлежит 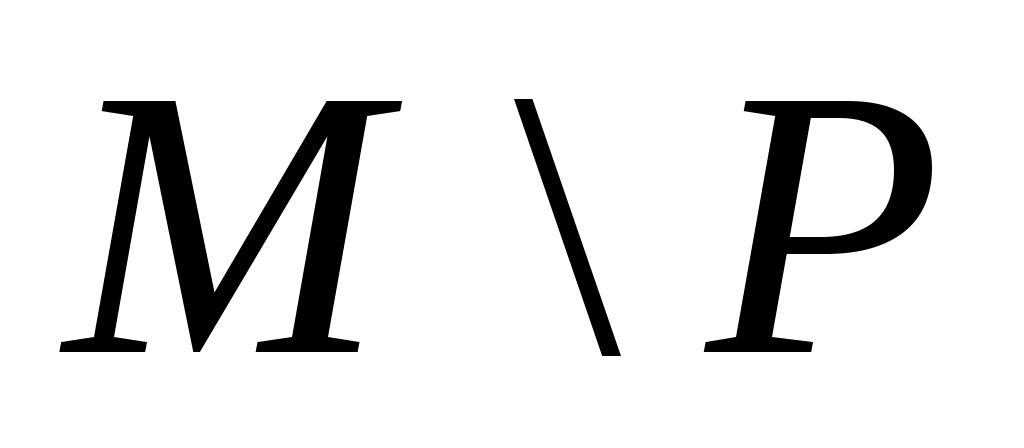 . Так как . Так как 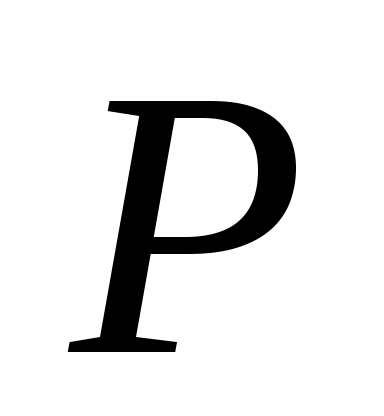 является является  -чередующейся цепью, то существует некоторое ребро из -чередующейся цепью, то существует некоторое ребро из 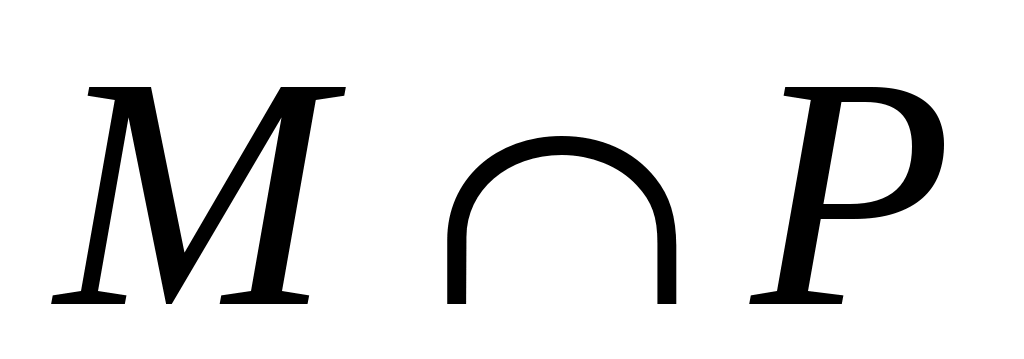 инцидентное инцидентное 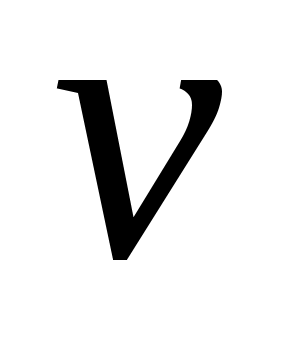 . Таким образом в . Таким образом в  существует два ребра существует два ребра 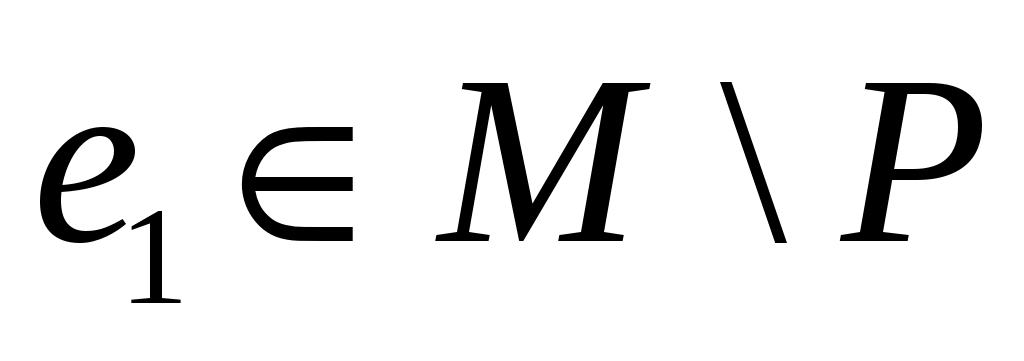 и и 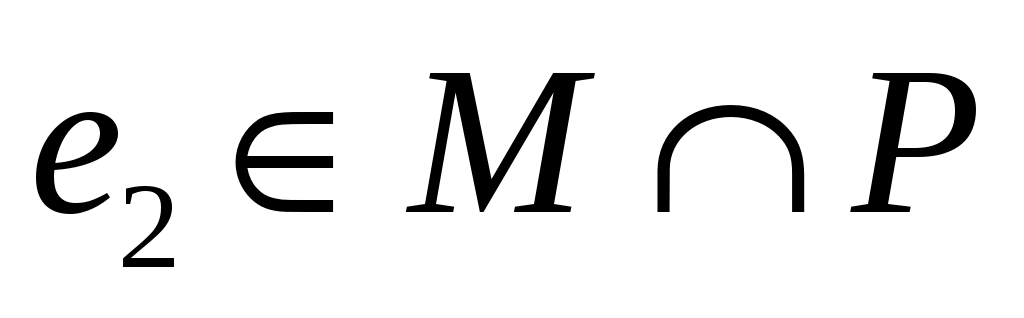 инцидентных инцидентных 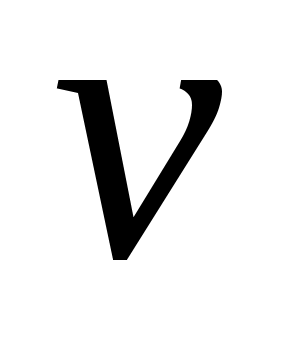 , чего не может быть. , чего не может быть. 
Следующая теорема является ключевой для большинства алгоритмов нахождения максимальных паросочетаний.
Теорема 6 (Берж, [2]). Паросочетание 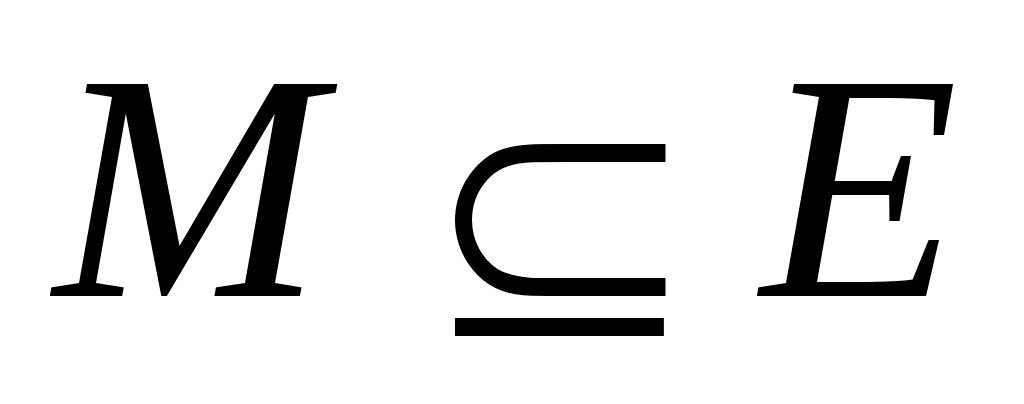 неориентированного графа неориентированного графа 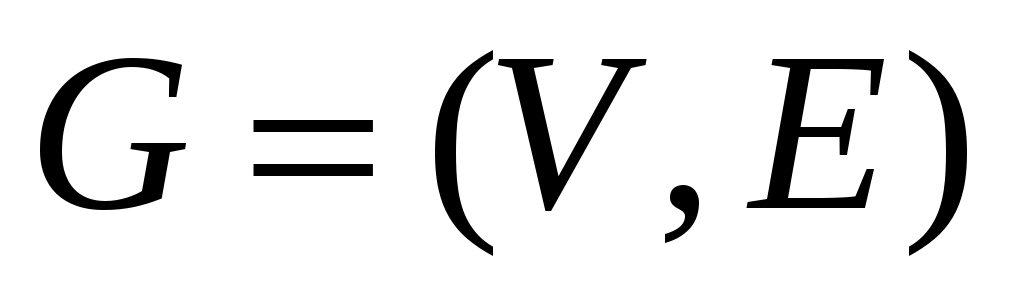 максимально тогда и только тогда, когда не существует максимально тогда и только тогда, когда не существует  -увеличивающих цепей. -увеличивающих цепей.
Доказательство. Из леммы 1 непосредственно следует необходимость отсутствия  -увеличивающих цепей. -увеличивающих цепей.
Докажем достаточность. Пусть  такое паросочетание в такое паросочетание в 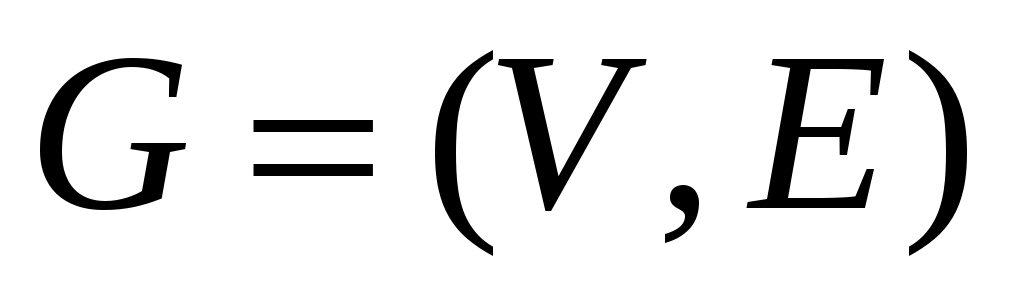 , для которого не существует , для которого не существует  -увеличивающих цепей. Предположим существует максимальное паросочетание -увеличивающих цепей. Предположим существует максимальное паросочетание 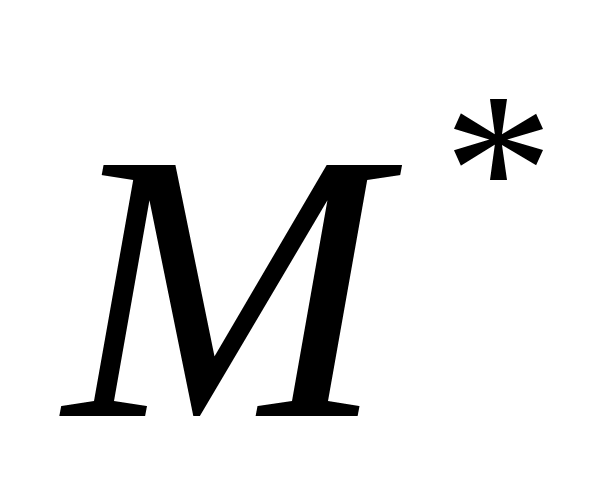 , такое что , такое что  . Рассмотрим граф . Рассмотрим граф 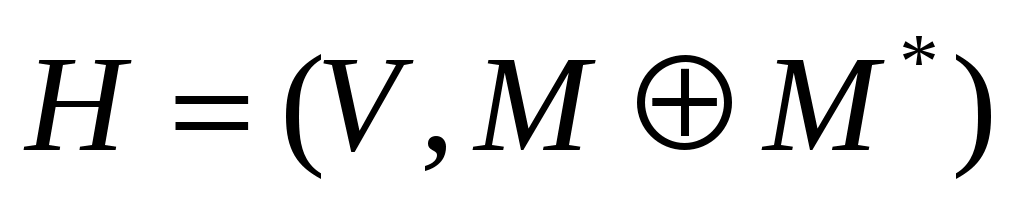 . Очевидно, что степень каждой вершины в . Очевидно, что степень каждой вершины в  не более 2, то есть граф не более 2, то есть граф  является объединением непересекающихся цепей и циклов. Заметим, что любые два ребра графа является объединением непересекающихся цепей и циклов. Заметим, что любые два ребра графа  инцидентных одной вершине таковы, что одно из них принадлежит инцидентных одной вершине таковы, что одно из них принадлежит  , а другое – , а другое – 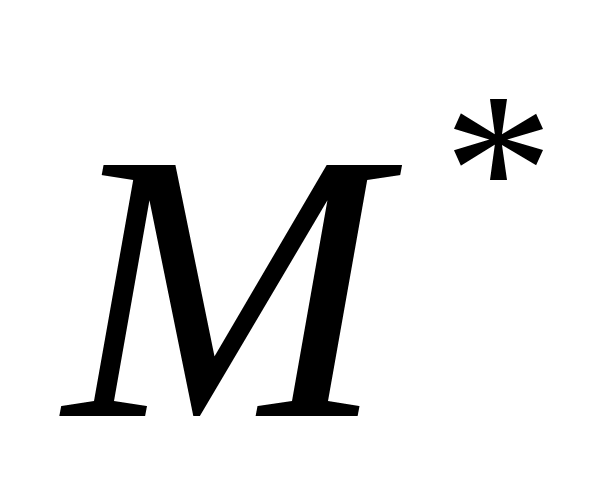 , следовательно, все циклы в графе , следовательно, все циклы в графе  – четные. Все цепи в – четные. Все цепи в  имеют четную длину, так как в противном случае они образовывали бы либо имеют четную длину, так как в противном случае они образовывали бы либо  -увеличивающие цепи, либо -увеличивающие цепи, либо 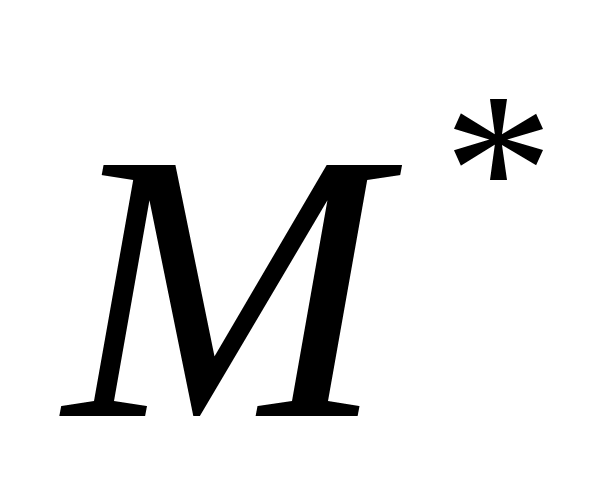 -увеличивающие цепи в графе -увеличивающие цепи в графе 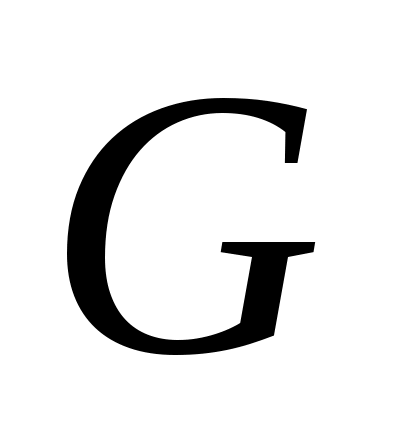 . Таким образом, в графе . Таким образом, в графе  содержится равное количество ребер из паросочетания содержится равное количество ребер из паросочетания  и из паросочетания и из паросочетания 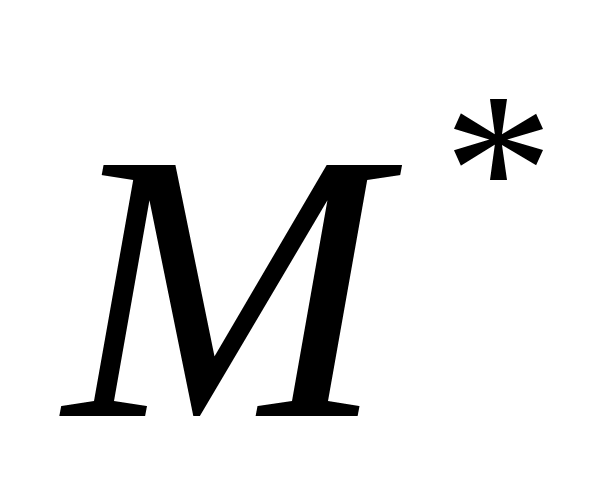 . Тогда . Тогда 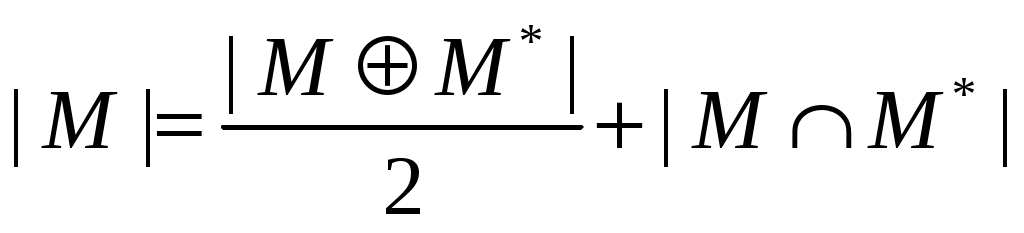 , но , но 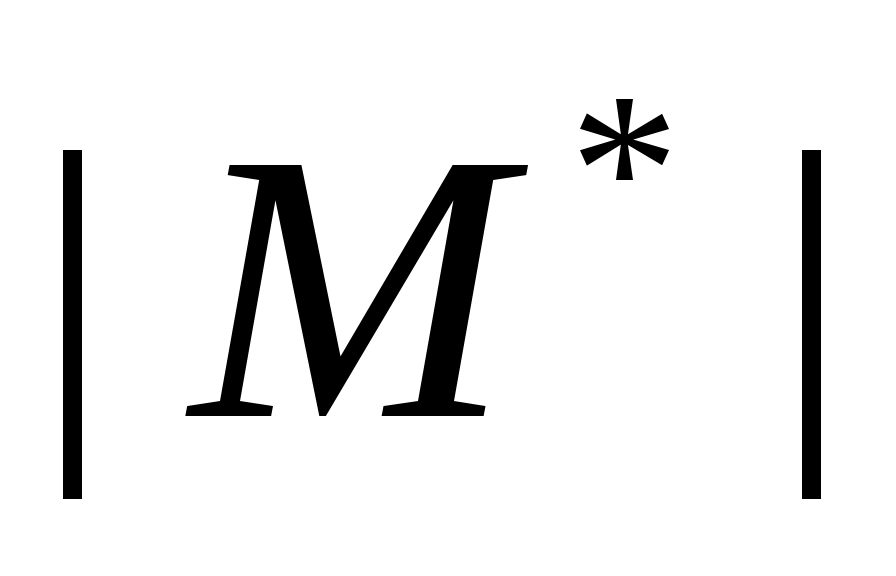 равна этой же величине, следовательно, равна этой же величине, следовательно, 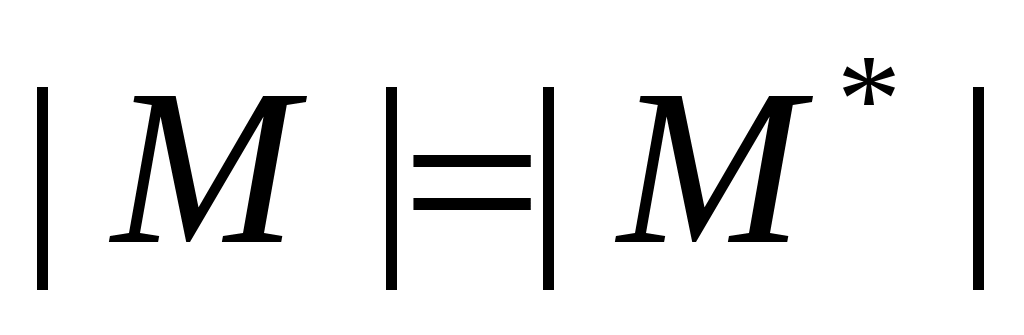 , что противоречит предположению , что противоречит предположению  . . 
Из теоремы 6 непосредственно следует метод нахождения максимального паросочетания.
Алгоритм 1
Вход: неориентированный граф 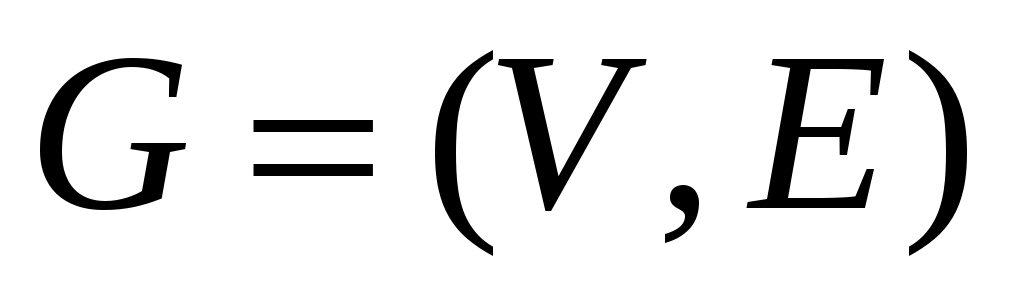 и паросочетание и паросочетание 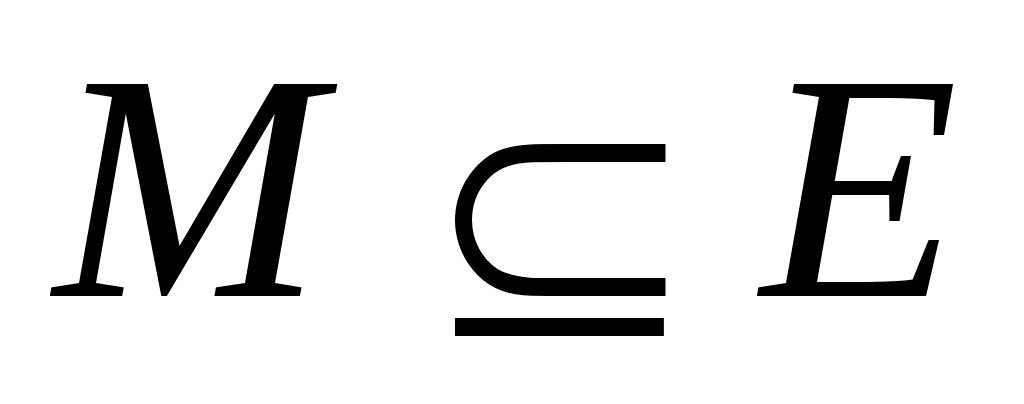 (возможно (возможно  ) )
Выход: максимальное паросочетание 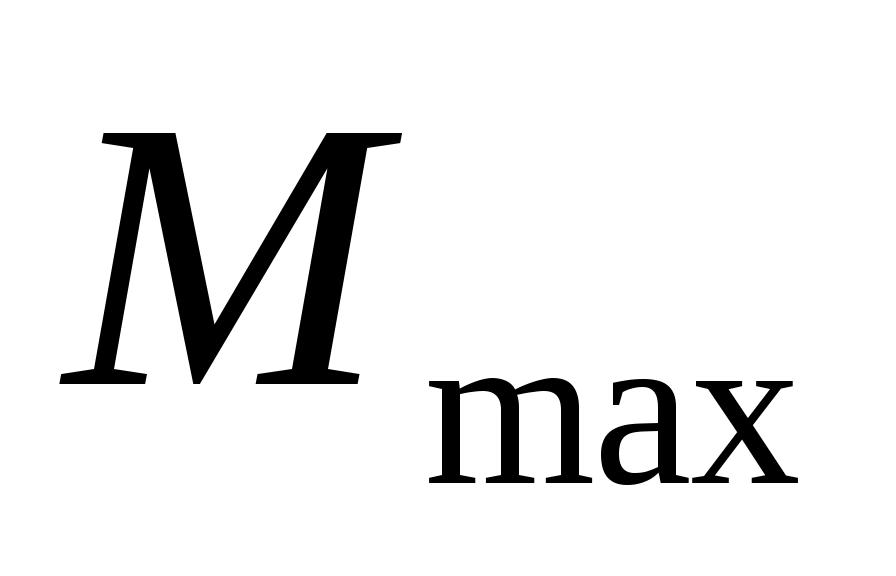
Метод:
01 while существует  -удлиняющая цепь do -удлиняющая цепь do
02 построить такую цепь 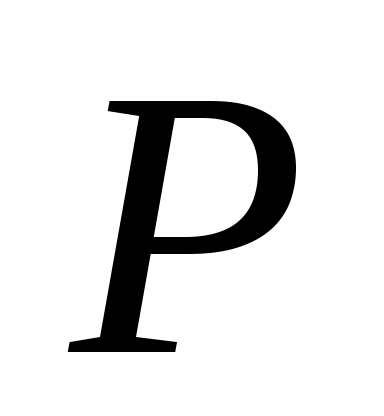
03 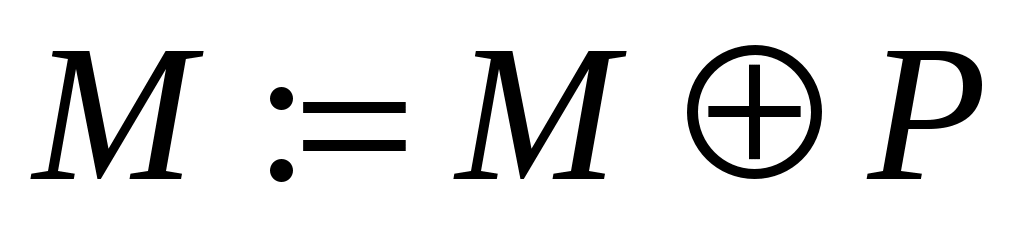
04 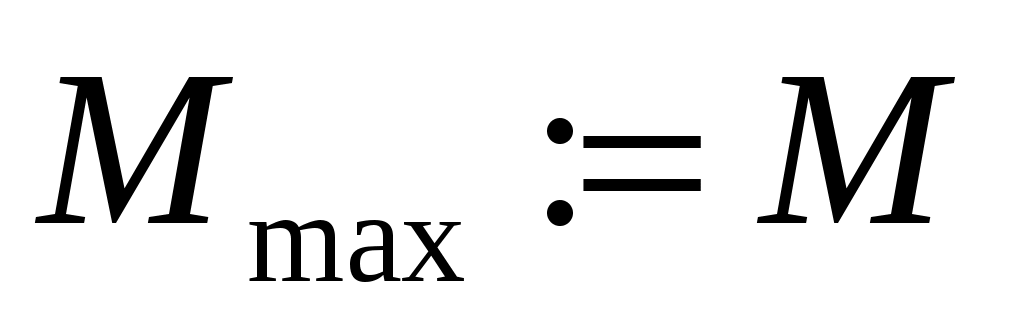
|
Заметим, что алгоритм 1 не является в некотором смысле алгоритмом, так как в нем не детализируется способ нахождения  -удлиняющей цепи. Так же важно отметить, что до настоящего момента мы рассматривали не обязательно двудольные графы и алгоритм 1 верен для графов в общем случае. -удлиняющей цепи. Так же важно отметить, что до настоящего момента мы рассматривали не обязательно двудольные графы и алгоритм 1 верен для графов в общем случае.
Ниже будет считать, что граф 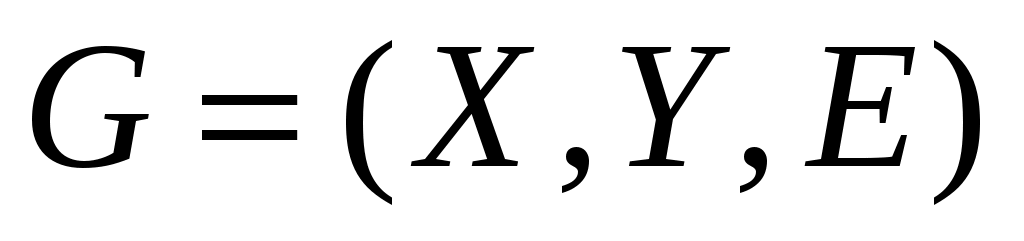 является двудольным. Построим новый ориентированный граф является двудольным. Построим новый ориентированный граф 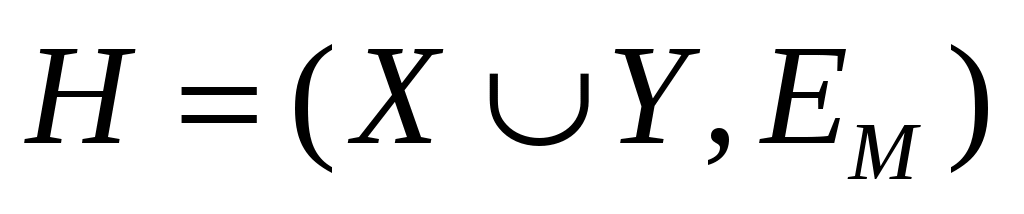 . Множество ориентированных ребер . Множество ориентированных ребер 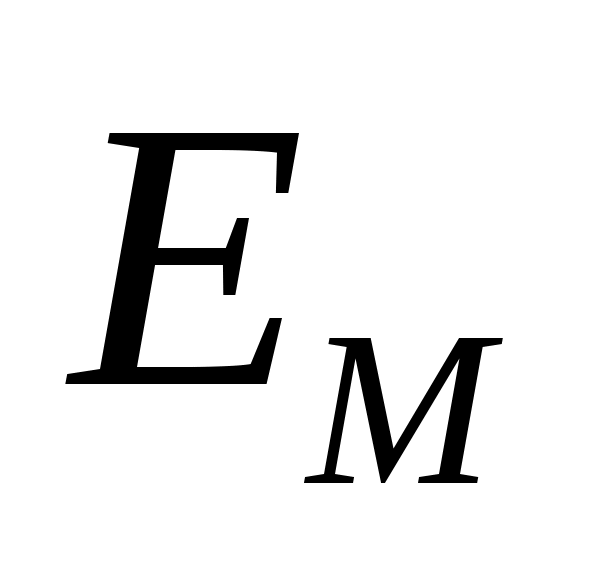 составлено из ребер множества составлено из ребер множества 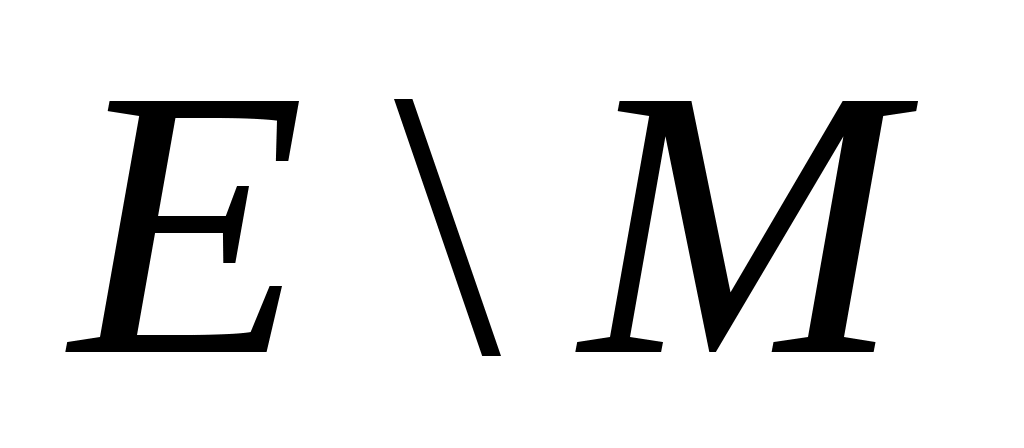 ориентированных от доли ориентированных от доли 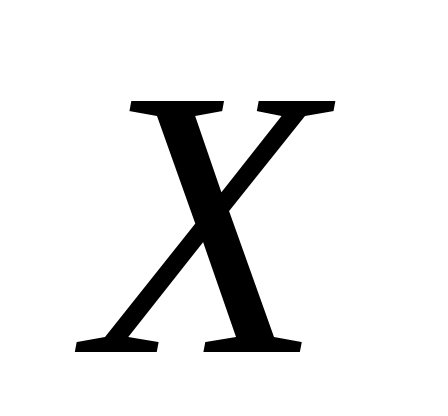 к доли к доли 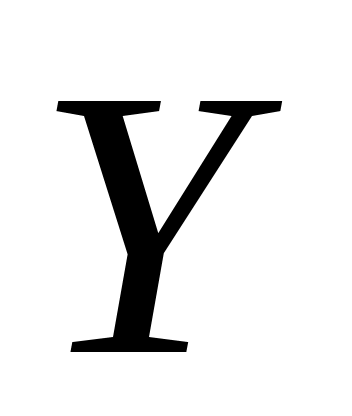 и ребер множества и ребер множества  ориентированных от ориентированных от 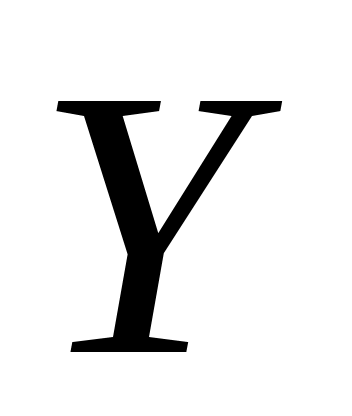 к к 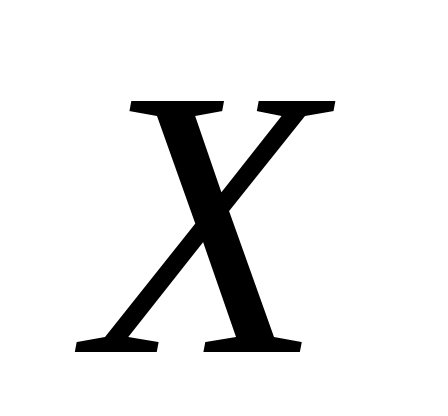 . .
На рис. 7 изображен соответствующий ориентированный граф  , соответствующий двудольному графу на рис. 6. , соответствующий двудольному графу на рис. 6.
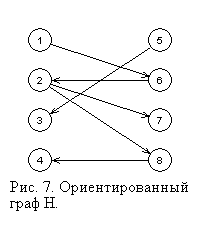
Очевидно следующее утверждение.
Утверждение 1. Если в орграфе  существует ориентированная цепь из ненасыщенной вершины доли существует ориентированная цепь из ненасыщенной вершины доли 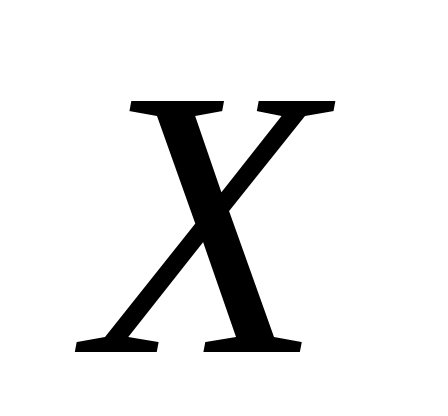 в ненасыщенную вершину доли в ненасыщенную вершину доли 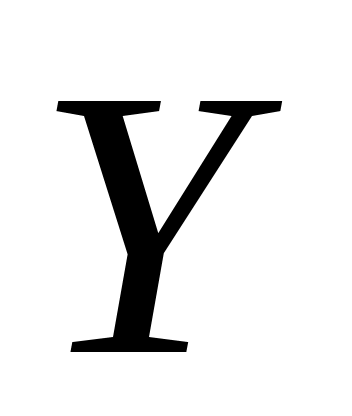 , то такой путь в графе , то такой путь в графе 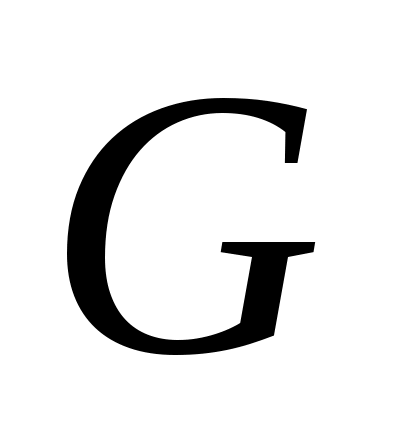 образует образует  -удлиняющую цепь. -удлиняющую цепь.
На рис. 6-7 ненасыщенными являются вершины 1 и 7. В графе  действительно существует цепь из 1 в 7: действительно существует цепь из 1 в 7: 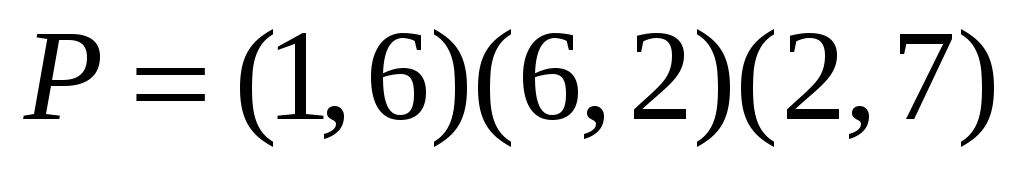 . Следовательно, паросочетание . Следовательно, паросочетание  можно увеличить можно увеличить 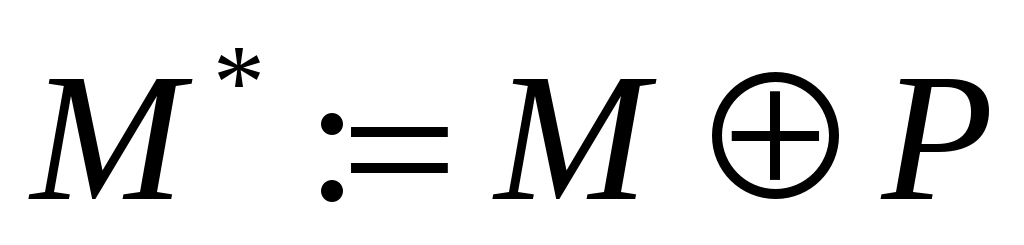 , где , где 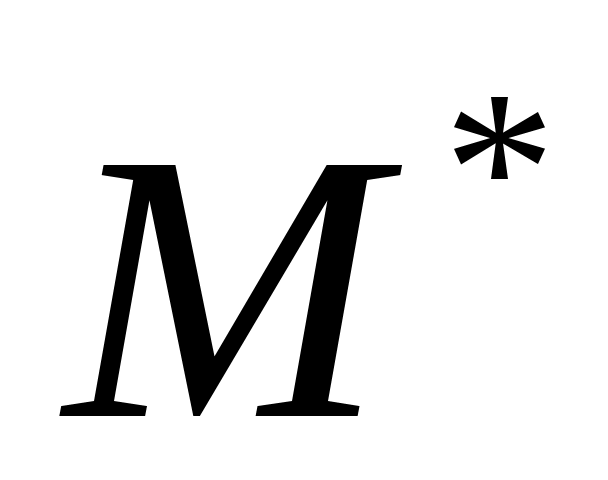 – увеличенное паросочетание. – увеличенное паросочетание.
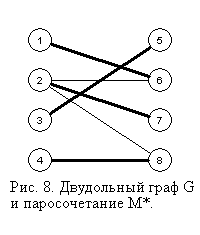
Если теперь по графу 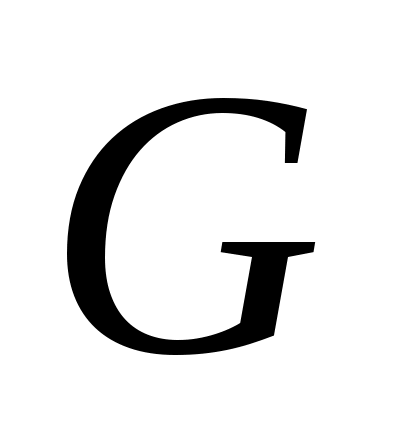 и паросочетанию и паросочетанию 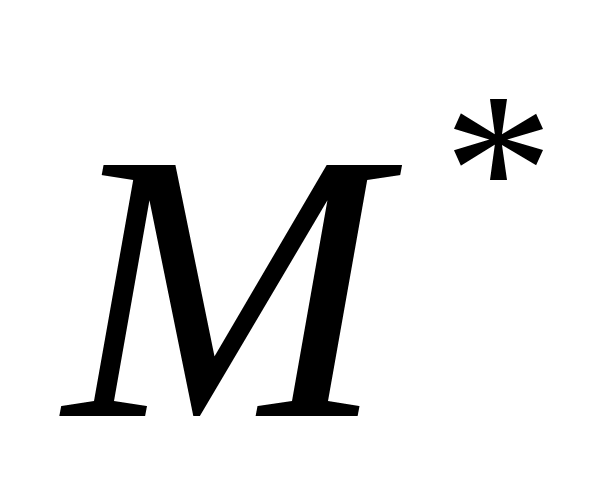 построить новый ориентированный граф построить новый ориентированный граф  , то в этом графе уже не будет ориентированной цепи из ненасыщенной вершины доли , то в этом графе уже не будет ориентированной цепи из ненасыщенной вершины доли 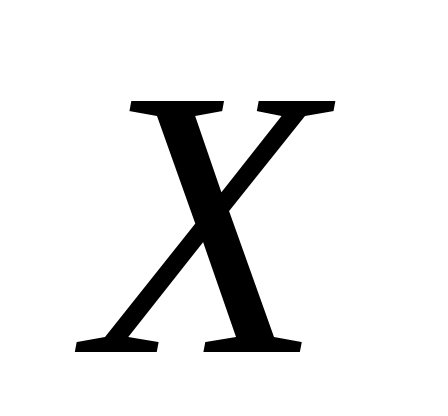 в ненасыщенную вершину доли в ненасыщенную вершину доли 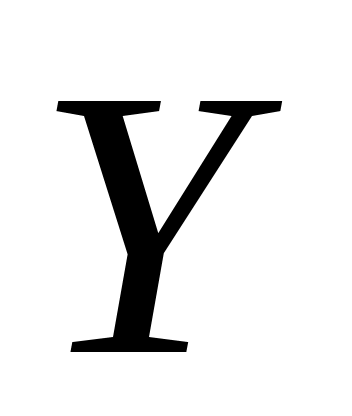 . Следовательно, паросочетание . Следовательно, паросочетание 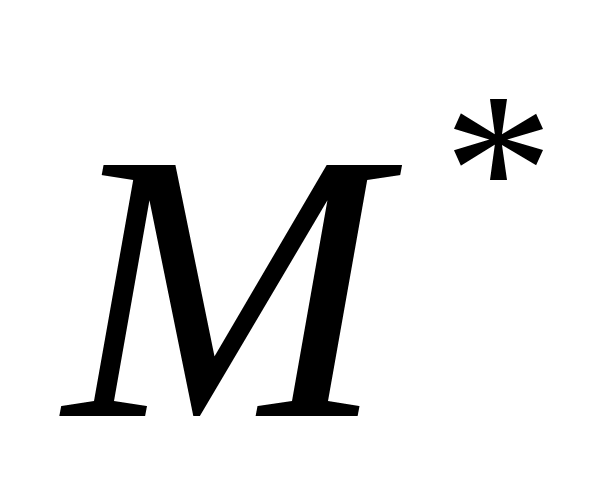 – максимальное. – максимальное.
Эти рассуждения подсказывают метод нахождения  -удлиняющих цепей (или факта их отсутствия). Заметим, что существование пути можно проверять за время -удлиняющих цепей (или факта их отсутствия). Заметим, что существование пути можно проверять за время 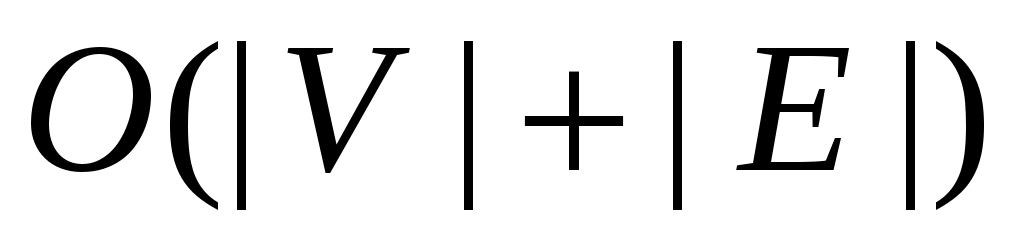 с помощью поиска в ширину или в глубину. с помощью поиска в ширину или в глубину.
Так как количество итерация цикла while алгоритма 1 не превосходит 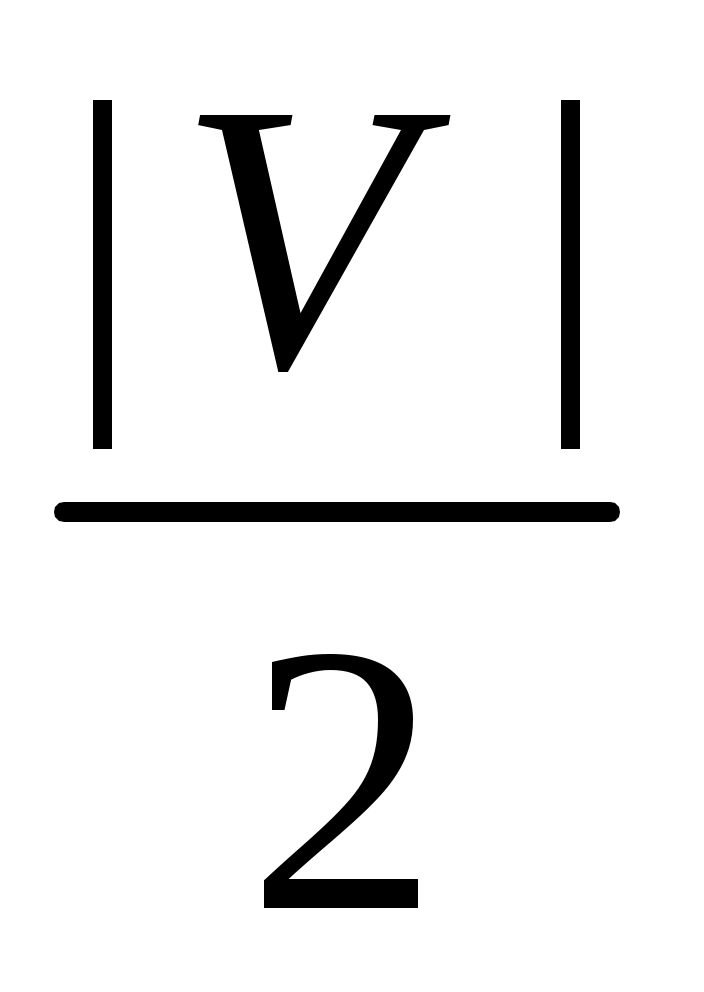 , то сложность алгоритма 1 при использования вышеописанной методики составляет , то сложность алгоритма 1 при использования вышеописанной методики составляет 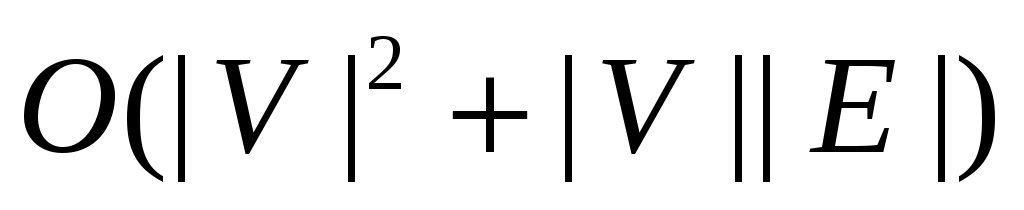 . .
Следующий алгоритм является своеобразной модификацией алгоритма 1.
Алгоритм 2 (алгоритм Куна)
Вход: неориентированный двудольный граф 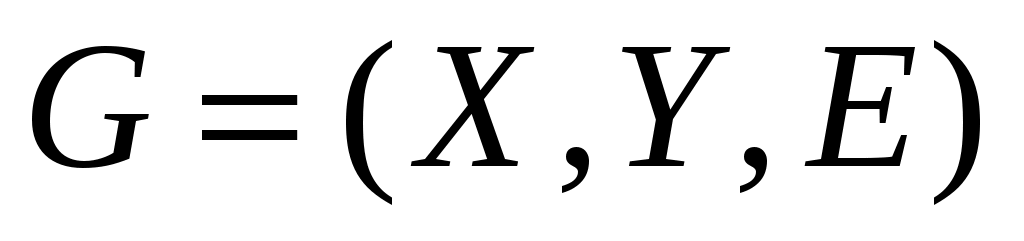
Выход: максимальное паросочетание
Метод:
function MAX_MATCHING_KHUN(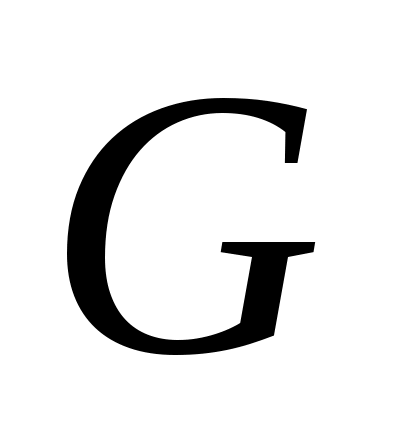 ) )
01 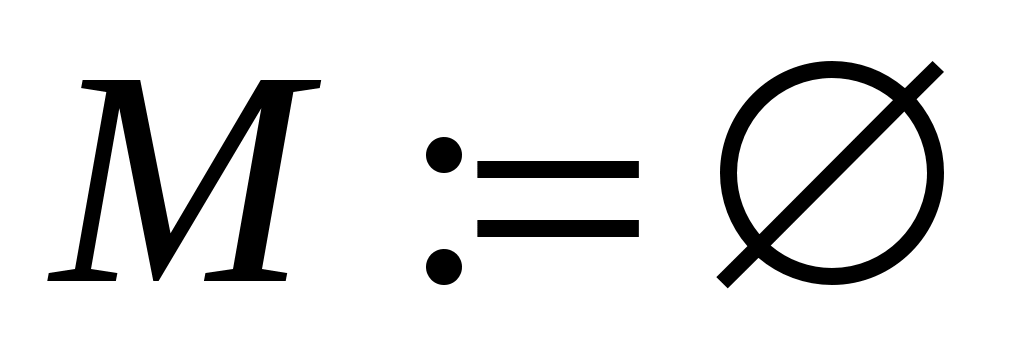
02 for 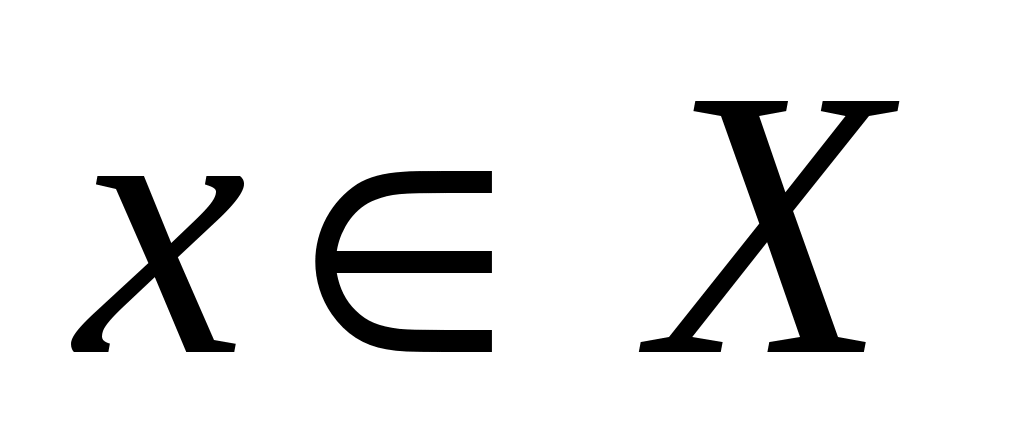 do do
03 Fill(used, FALSE)
04 TRY_KHUN( ) )
05 return 
end
|
Алгоритм 2 в строке 04 использует функцию TRY_KHUN( ). ).
Функция TRY_KHUN( ). ).
Вход: вершина  множества множества 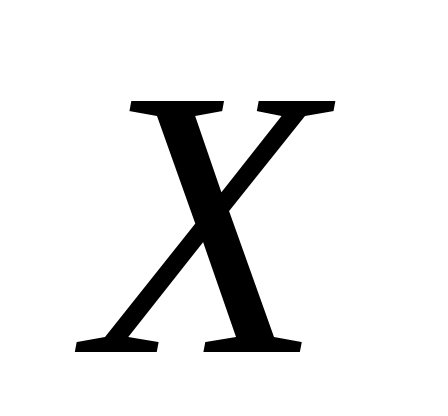
Выход: TRUE или FALSE (найдена ли  -удлиняющая цепь из вершины -удлиняющая цепь из вершины  ) )
Глобальные переменные: двудольный граф 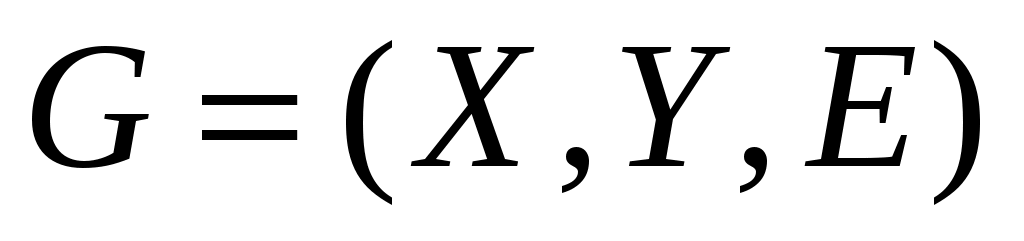 , паросочетание , паросочетание  , булевский массив used, проиндексиванный элементами множества , булевский массив used, проиндексиванный элементами множества 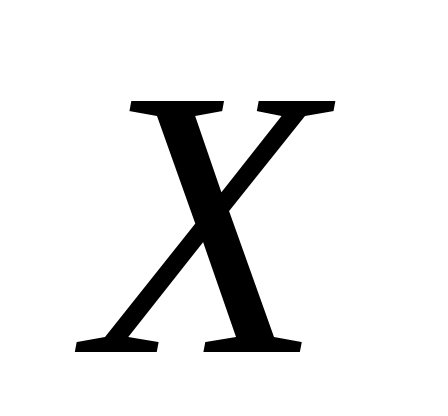
Метод:
function TRY_KHUN( ) )
01 if used[ ] then ] then
02 return FALSE
03 used[ ] := TRUE ] := TRUE
04 for 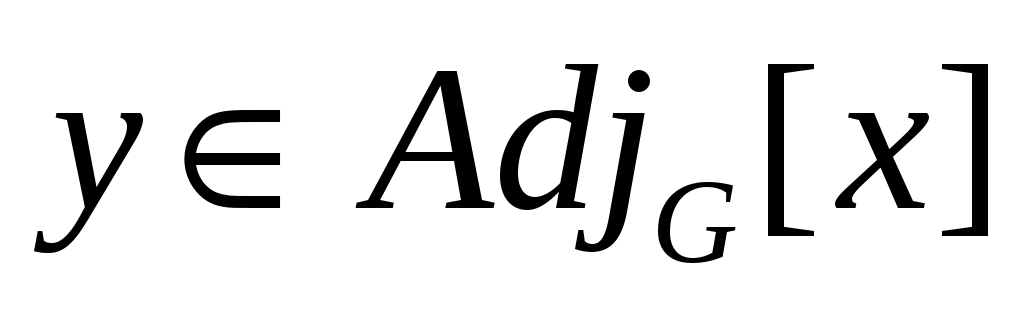 do do
05 if (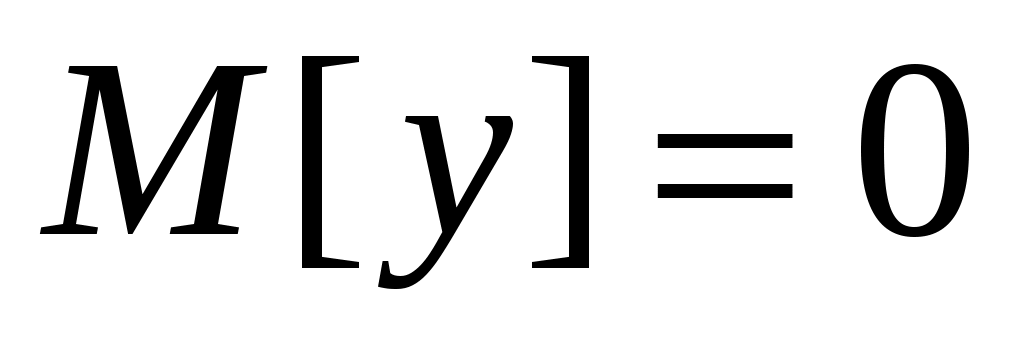 ) or (TRY_KHUN( ) or (TRY_KHUN(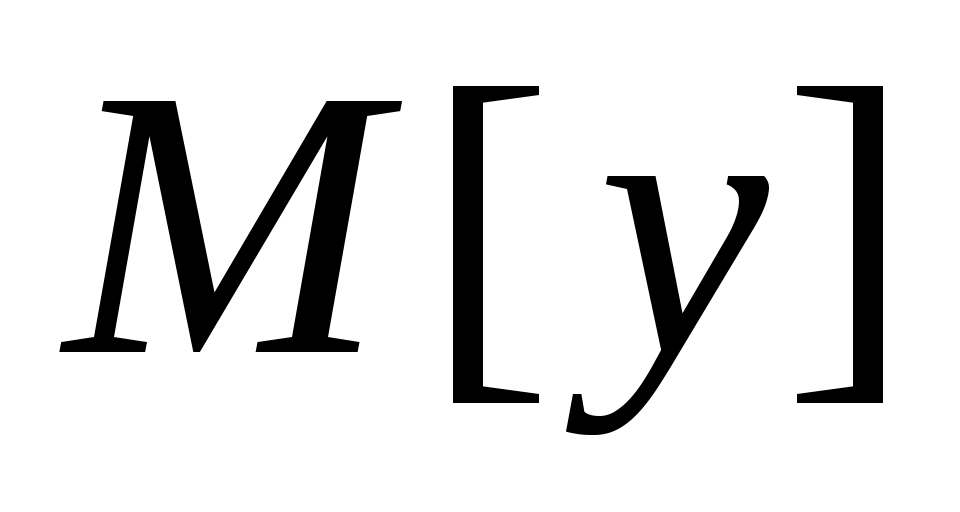 )) then )) then
06 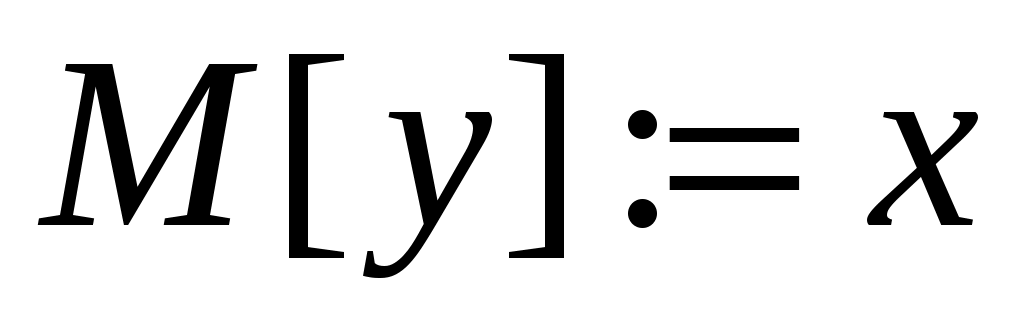
07 return TRUE
08 return FALSE
end
|
В описании функции TRY_KHUN( ) используется, что паросочетание ) используется, что паросочетание  хранится в виде массива, проиндексированного элементами множества хранится в виде массива, проиндексированного элементами множества 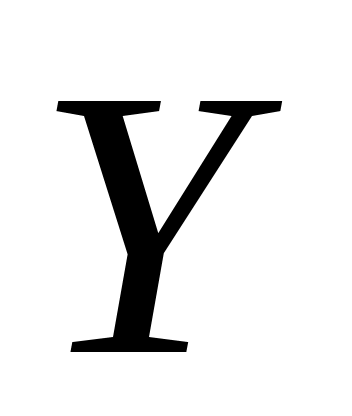 . .
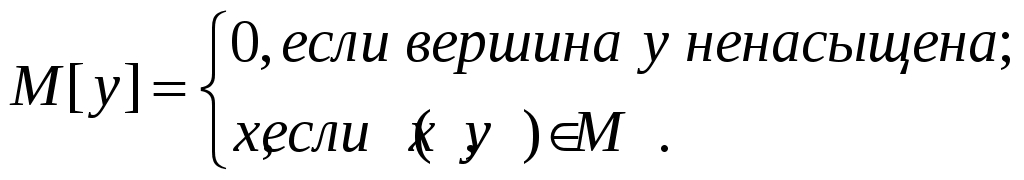
Присвоение в строке 06 обозначает, что ребро 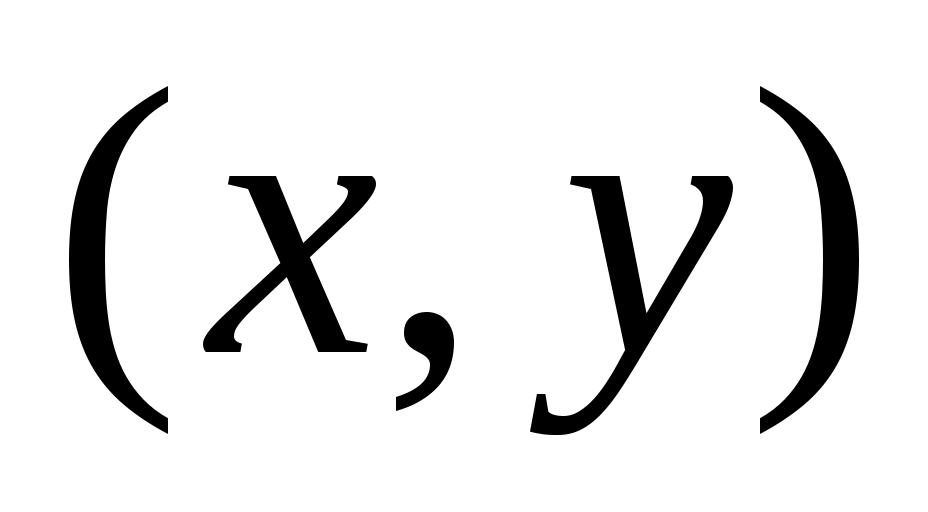 добавляется в добавляется в  (при этом из (при этом из  при необходимости удаляется другое ребро инцидентное при необходимости удаляется другое ребро инцидентное 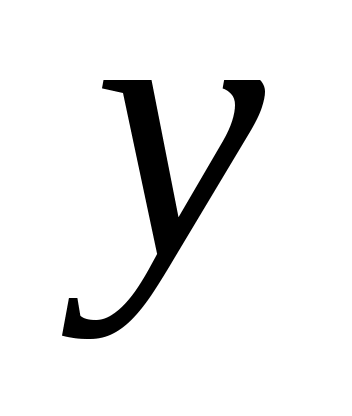 ). Символ ). Символ  в строке 04 обозначает множество вершин смежных с вершиной в строке 04 обозначает множество вершин смежных с вершиной  в графе в графе 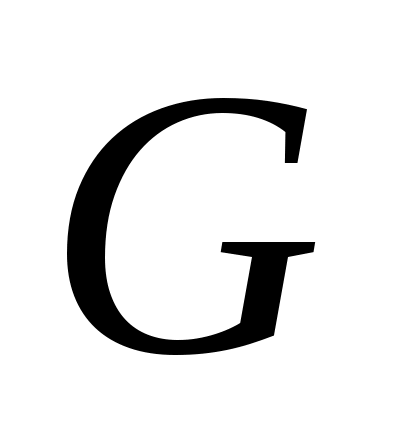 . В строке 05 предполагается, что TRY_KHUN( . В строке 05 предполагается, что TRY_KHUN(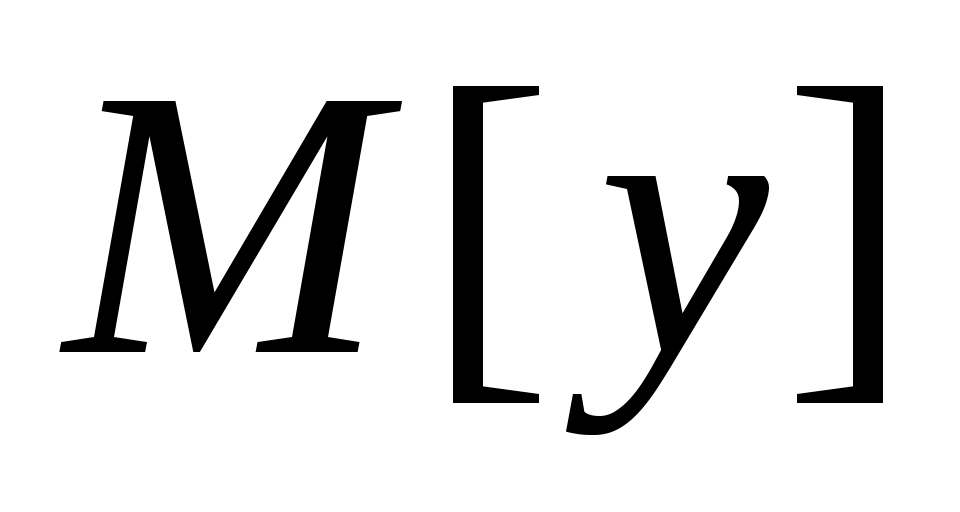 ) не вызывается, если ) не вызывается, если 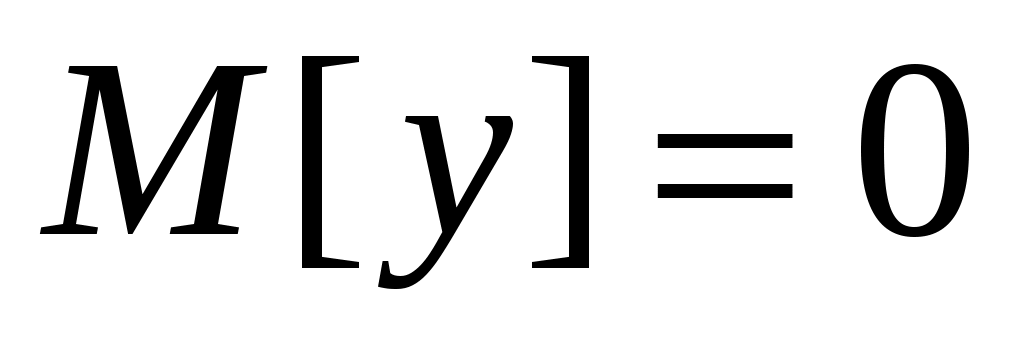 (что соответствует стандартной оптимизации булевских выражений в современных языках программирования). (что соответствует стандартной оптимизации булевских выражений в современных языках программирования).
Теорема 7. Алгоритм 2 – корректен.
Пусть вершины множества 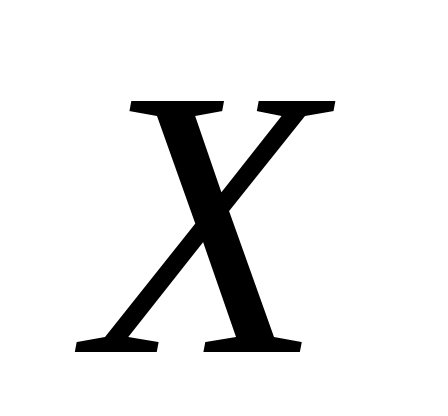 перебираются в порядке перебираются в порядке 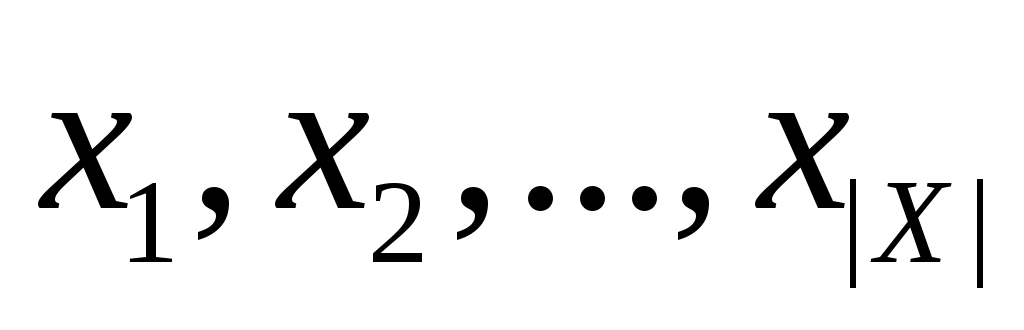 в стоке 02 алгоритма 2. Ниже символом в стоке 02 алгоритма 2. Ниже символом 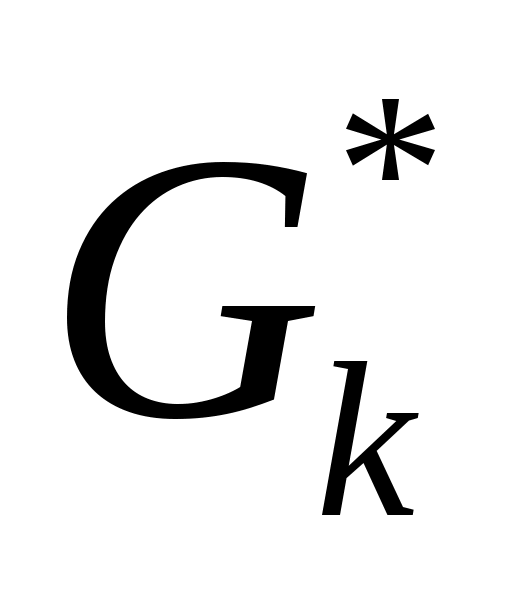 будет обозначать граф будет обозначать граф 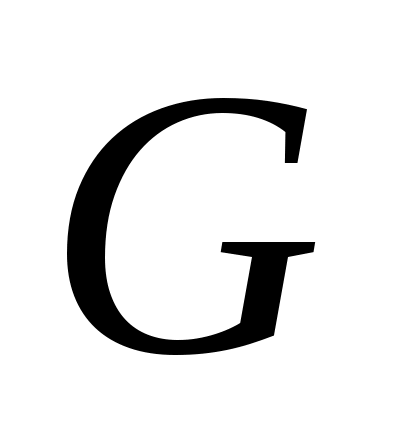 , из которого удалили вершины , из которого удалили вершины 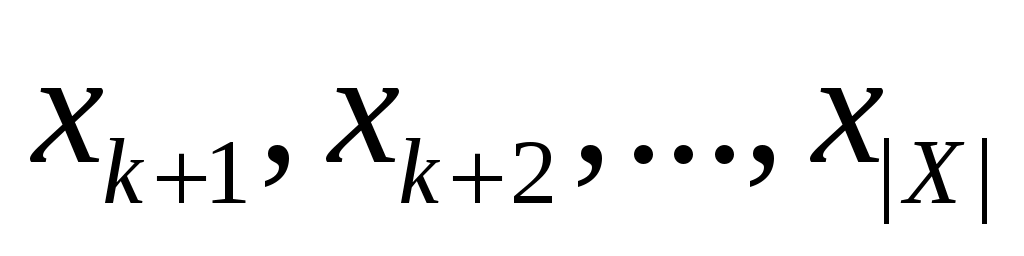 и инцидентные им ребра. и инцидентные им ребра.
Покажем, что выполняется следующий инвариант: после 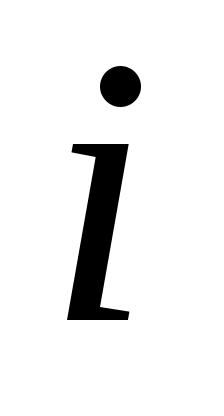 -го выполнения строки 04 алгоритма 2 в -го выполнения строки 04 алгоритма 2 в  содержится максимальное паросочетание для графа содержится максимальное паросочетание для графа 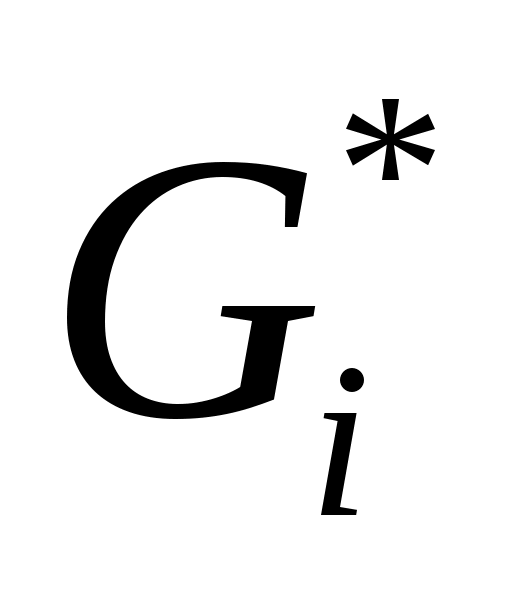 . Докажем это утверждение по индукции. В самом деле, после первой итерации цикла в паросочетании . Докажем это утверждение по индукции. В самом деле, после первой итерации цикла в паросочетании  будет содержаться ребро, если и только если вершина будет содержаться ребро, если и только если вершина 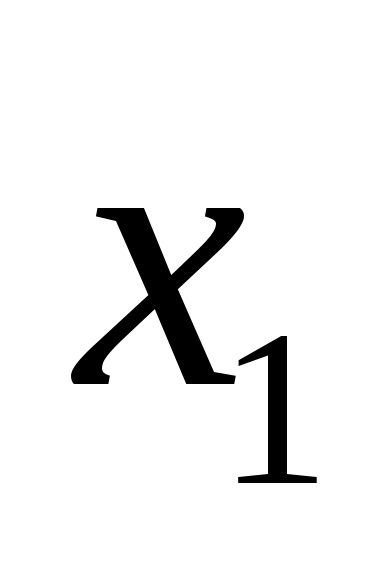 не изолированная. не изолированная.
Заметим, что TRY_KHUN(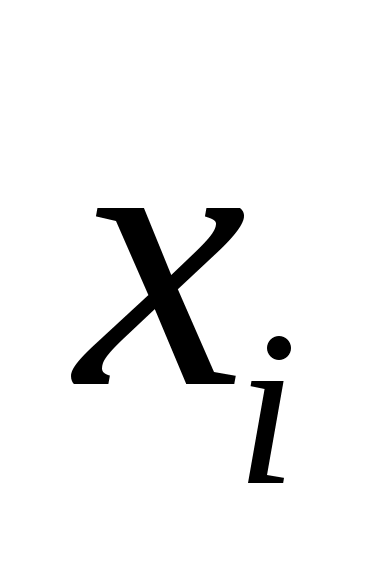 ) фактически пытается найти с помощью поиска в глубину ) фактически пытается найти с помощью поиска в глубину  -удлиняющую цепь из -удлиняющую цепь из 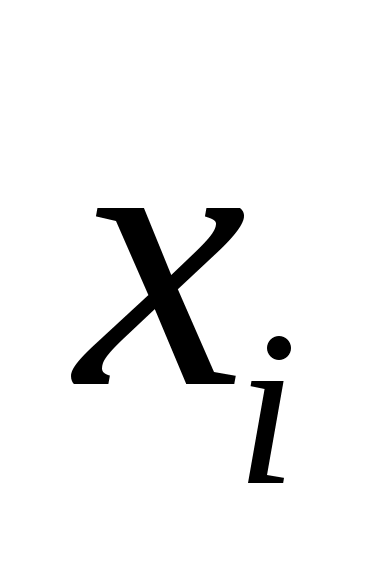 и, в случае успеха, заменяет и, в случае успеха, заменяет  на на  , где , где 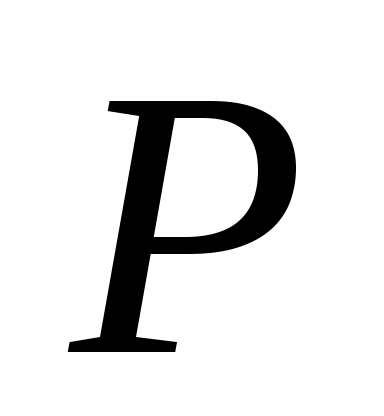 – найденная цепь, и возвращает TRUE. – найденная цепь, и возвращает TRUE.
Рассмотрим 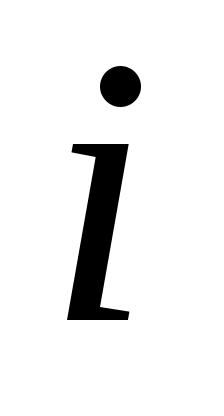 -ую итерацию цикла 02-04. В вызове TRY_KHUN( -ую итерацию цикла 02-04. В вызове TRY_KHUN(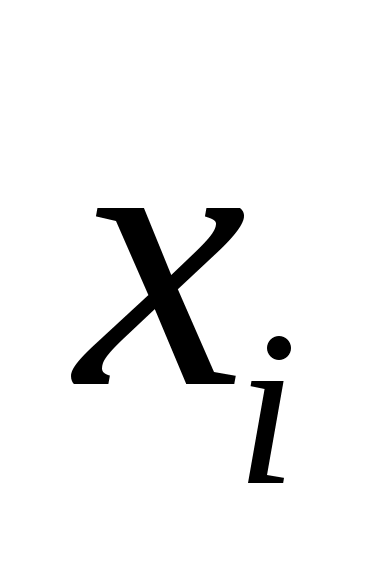 ) все рекурсивные вызовы TRY_KHUN будут только от вершин ) все рекурсивные вызовы TRY_KHUN будут только от вершин 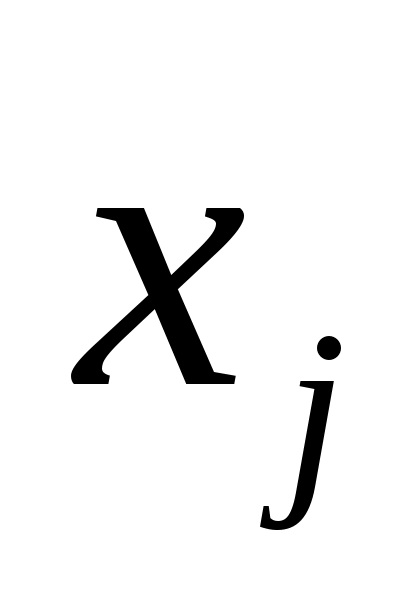 , где , где 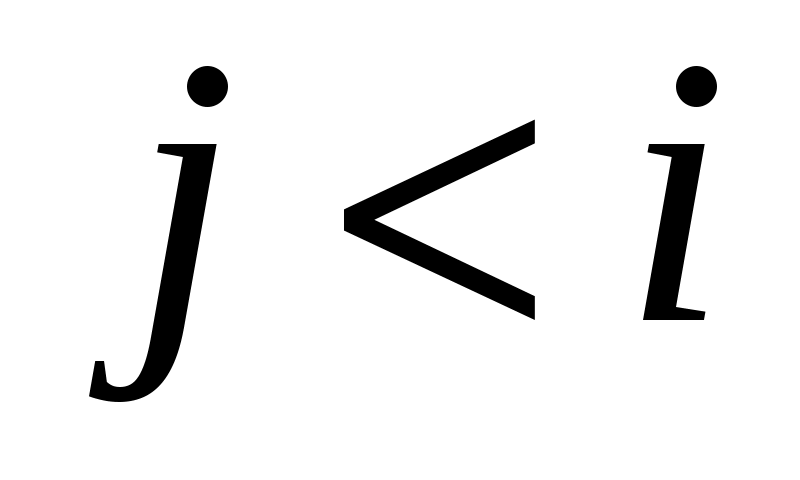 . Максимальное паросочетание для графа . Максимальное паросочетание для графа 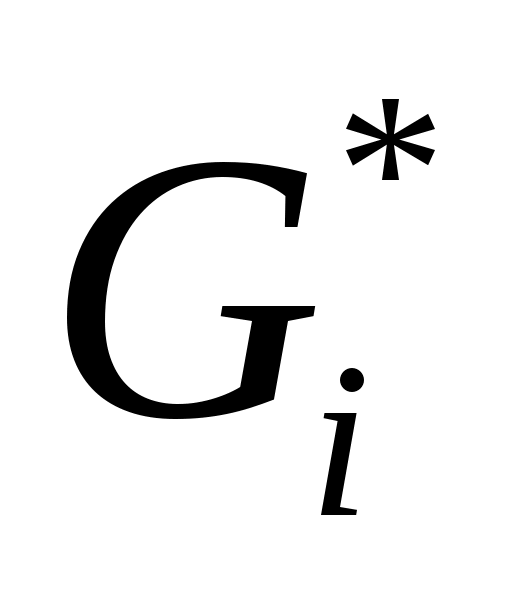 может быть больше, чем для графа может быть больше, чем для графа 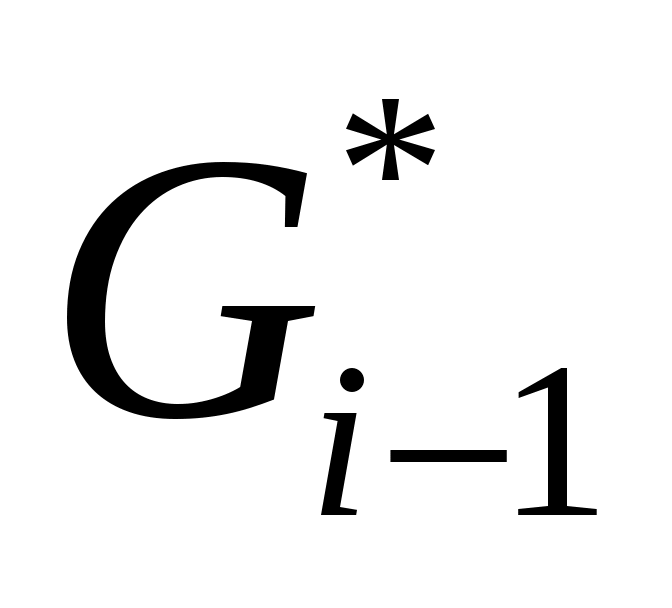 максимум на одно ребро. В этом случае в максимум на одно ребро. В этом случае в 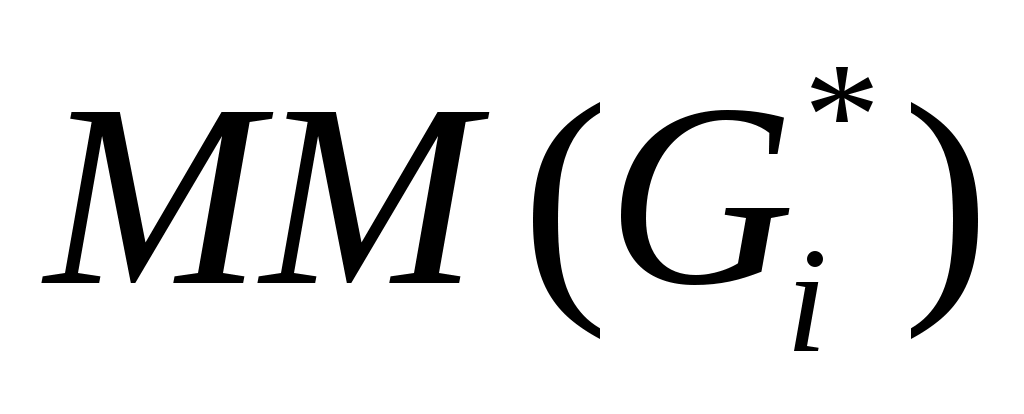 обязательно найдется ребро инцидентное обязательно найдется ребро инцидентное 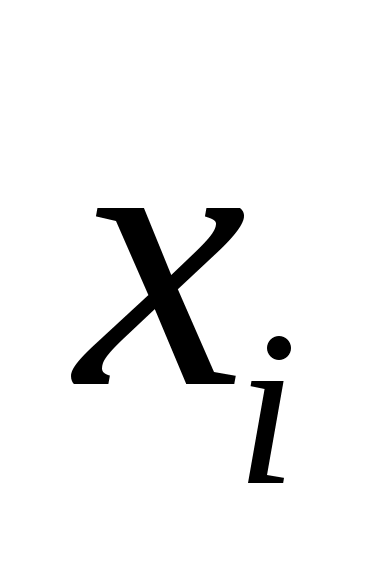 , но так как эта вершина не насыщена паросочетанием , но так как эта вершина не насыщена паросочетанием 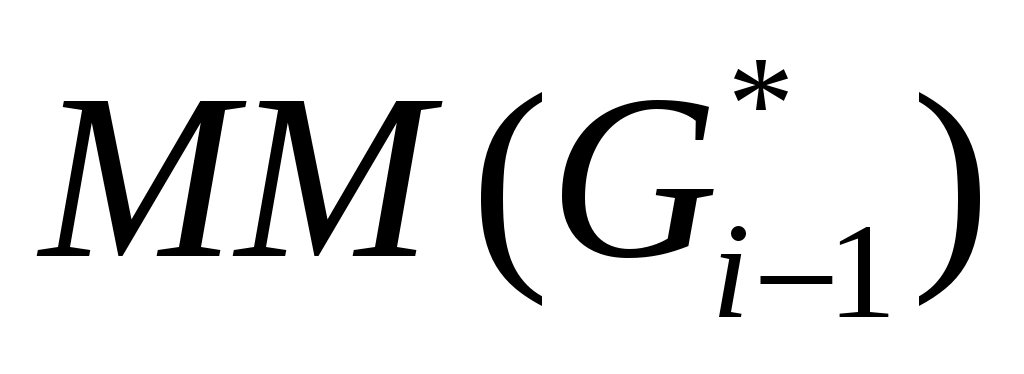 , то чтобы перейти от , то чтобы перейти от 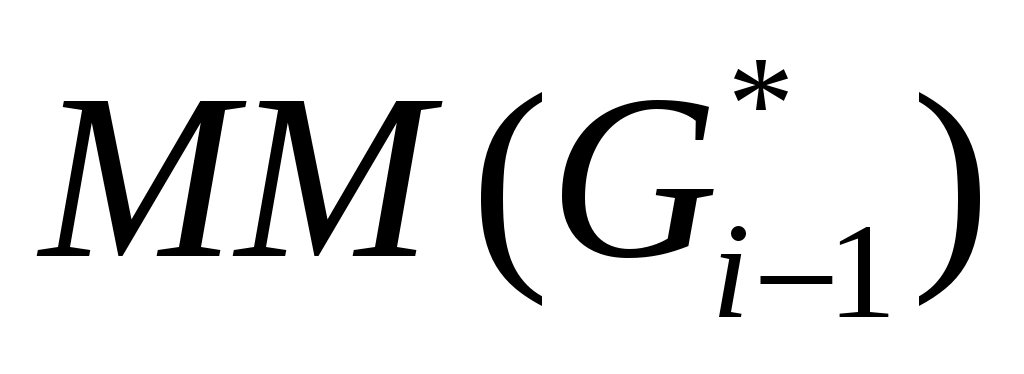 к к 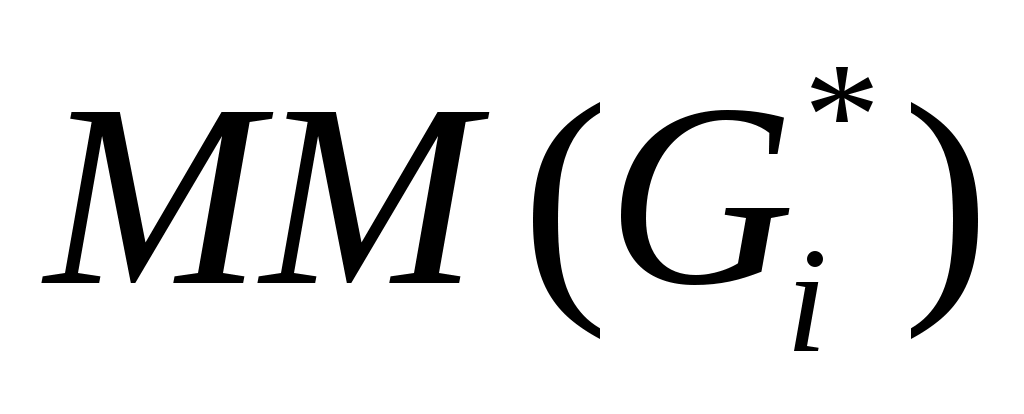 достаточно найти удлиняющую цепочку из вершины достаточно найти удлиняющую цепочку из вершины 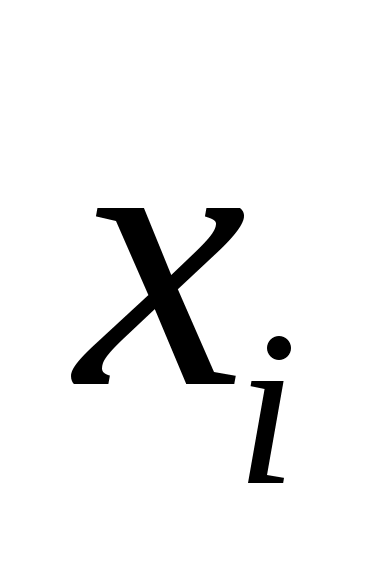 , что и делает TRY_KHUN( , что и делает TRY_KHUN(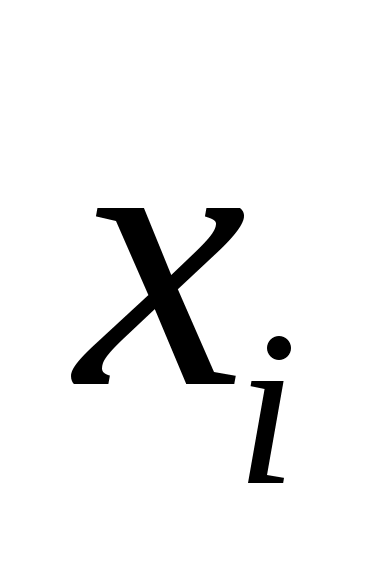 ). Таким образом, в предположении, что инвариант верен на ). Таким образом, в предположении, что инвариант верен на 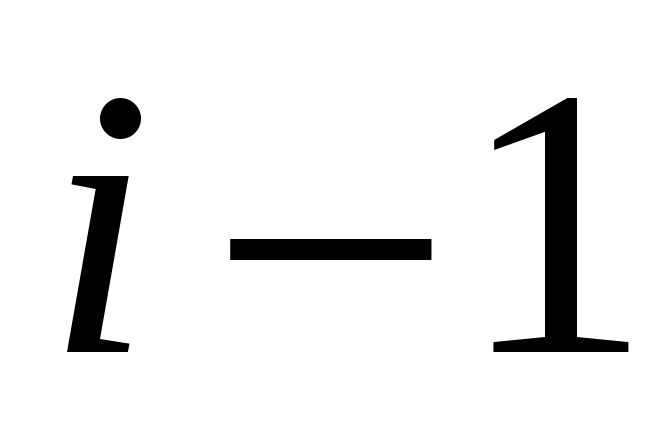 -ой итерации, удалось доказать, что инвариант сохраняется и на -ой итерации, удалось доказать, что инвариант сохраняется и на 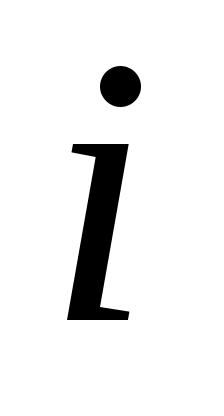 -ой итерации. Значит, инвариант выполняется на любой итерации, то есть в конце алгоритма, так как -ой итерации. Значит, инвариант выполняется на любой итерации, то есть в конце алгоритма, так как 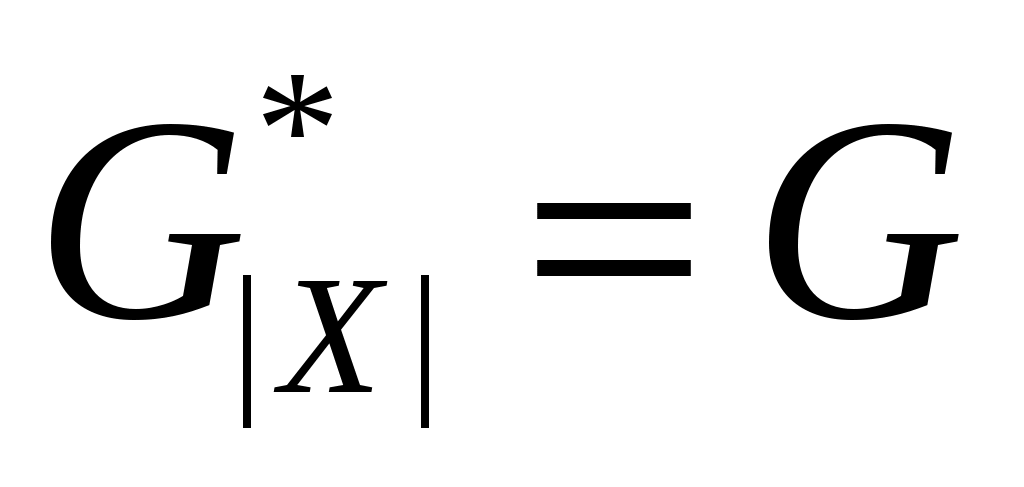 , ,  суть максимальное паросочетание. суть максимальное паросочетание. 
Утверждение 2. Если в процессе алгоритма 2 вершина 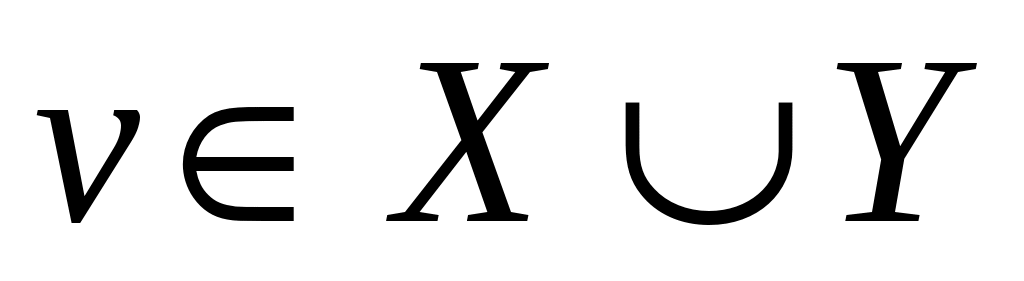 насытилась некоторым промежуточным паросочетанием, то насытилась некоторым промежуточным паросочетанием, то 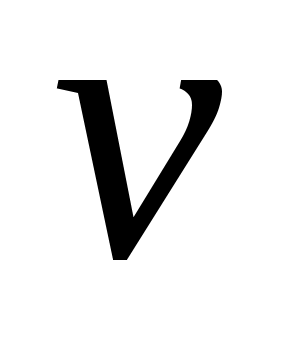 останется насыщенной до конца выполнения алгоритма 2. останется насыщенной до конца выполнения алгоритма 2.
Утверждение 3. Если на 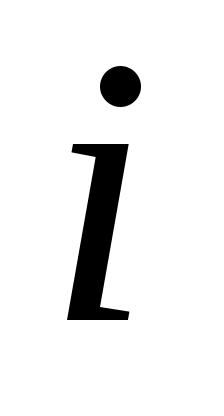 -ой итерации цикла 02-04 алгоритма 2 вершина -ой итерации цикла 02-04 алгоритма 2 вершина 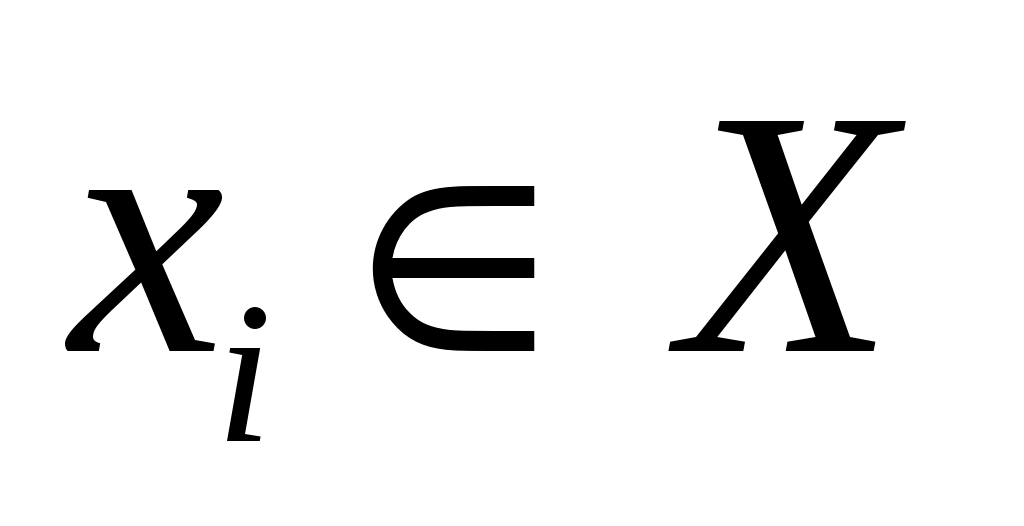 не насытилась в ходе выполнения TRY_KHUN( не насытилась в ходе выполнения TRY_KHUN(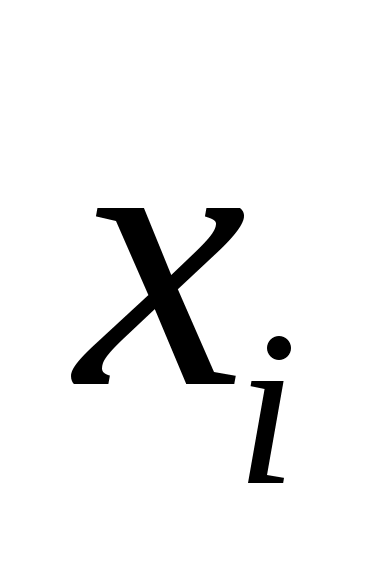 ), то ), то 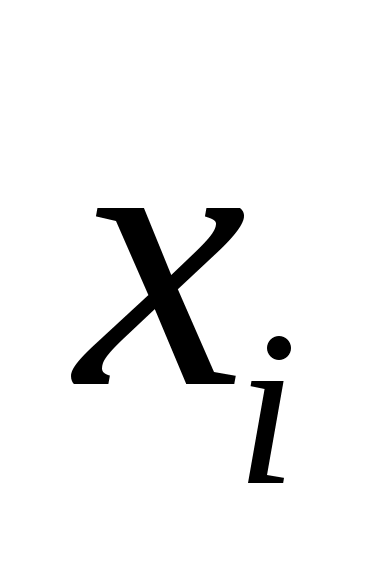 останется ненасыщенной до конца выполнения алгоритма 2. останется ненасыщенной до конца выполнения алгоритма 2.
Сложность алгоритма 2 составляет, очевидно, величину 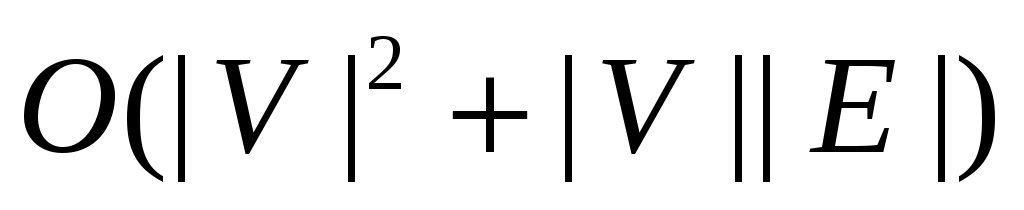 . Можно попытаться оценить его сложность точнее. Предположим . Можно попытаться оценить его сложность точнее. Предположим 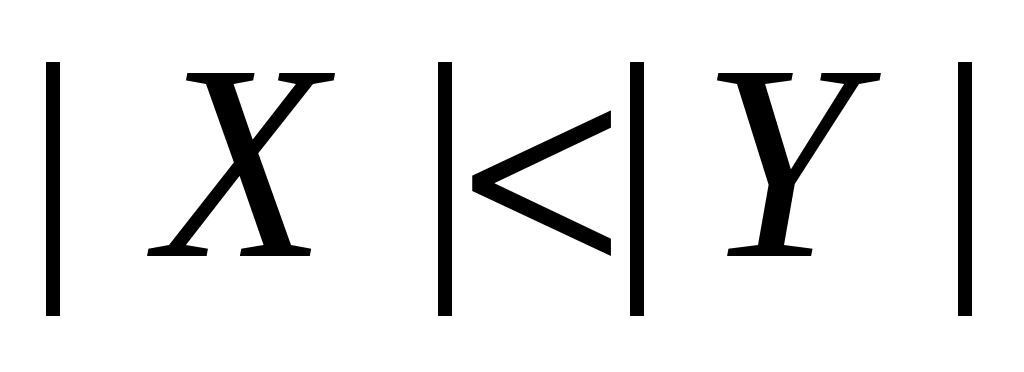 , тогда цикл 02-04 выполнится , тогда цикл 02-04 выполнится 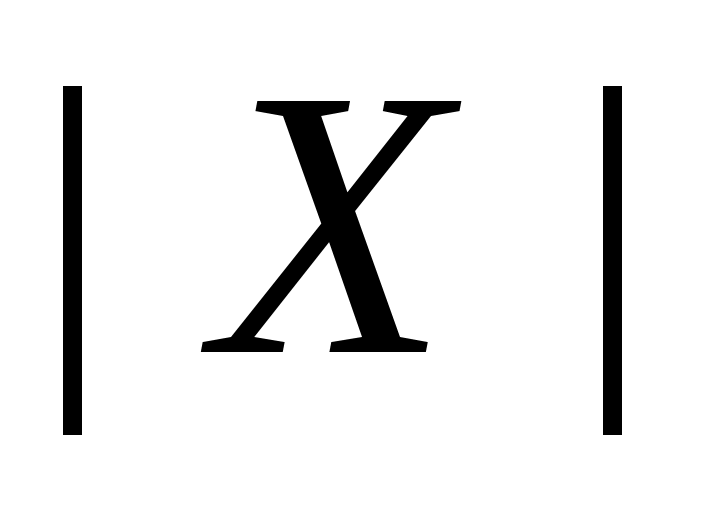 раз. Оценим время работы каждого вызова TRY_KHUN( раз. Оценим время работы каждого вызова TRY_KHUN( ) строки 04. Каждый вызов TRY_KHUN( ) строки 04. Каждый вызов TRY_KHUN( ) (в том числе и рекурсивные вызовы) на первый взгляд работают за ) (в том числе и рекурсивные вызовы) на первый взгляд работают за 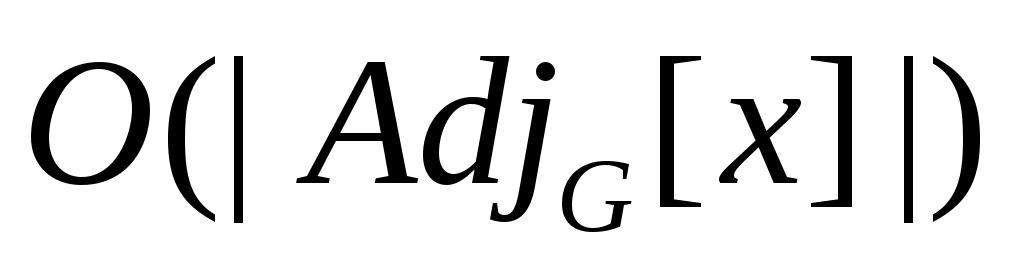 действий (разумеется, имеются в виду те вызовы, которые проходят проверку в строке 01). На самом деле, каждая итерация цикла 04-07 либо соответствует одному ребру из действий (разумеется, имеются в виду те вызовы, которые проходят проверку в строке 01). На самом деле, каждая итерация цикла 04-07 либо соответствует одному ребру из  , либо мгновенно успешно завершает вызов (если , либо мгновенно успешно завершает вызов (если 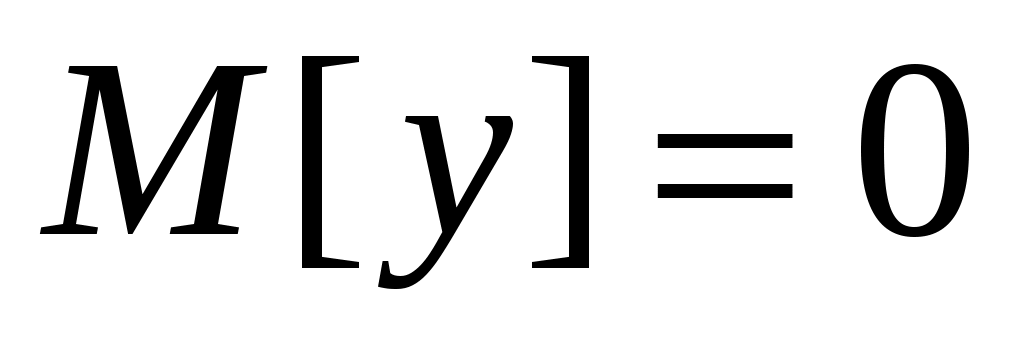 ). Поэтому верно, что каждый вызов TRY_KHUN( ). Поэтому верно, что каждый вызов TRY_KHUN( ) работает за ) работает за 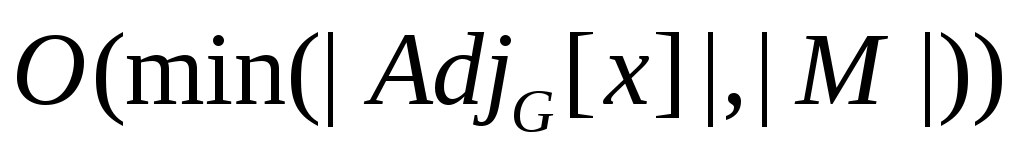 . Так как . Так как  , то один вызов TRY_KHUN( , то один вызов TRY_KHUN(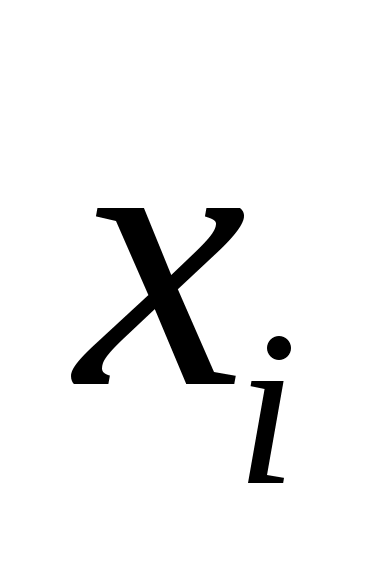 ) (в него включаются все необходимые рекурсивные вызовы) работает за ) (в него включаются все необходимые рекурсивные вызовы) работает за 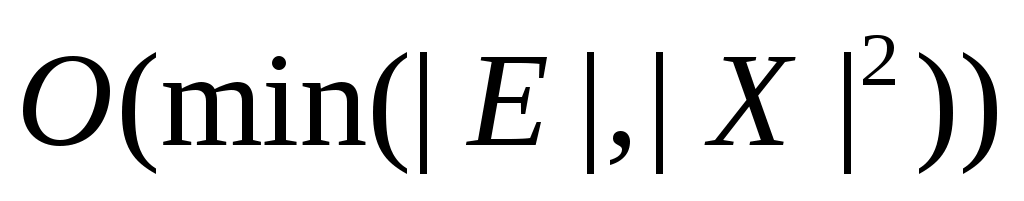 , а, значит, весь алгоритм 2 выполняется за время , а, значит, весь алгоритм 2 выполняется за время 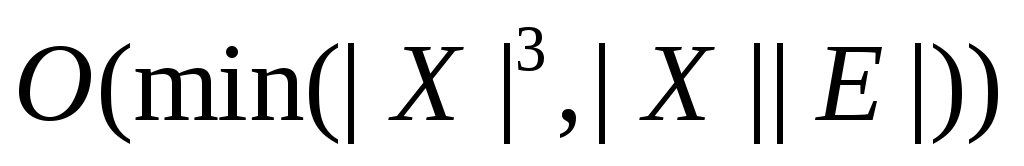 . .
Заметим, что можно очень просто сильно ускорить алгоритм 2 (впрочем, как и алгоритм 1). Если в алгоритме 2 строки 01 и 04 немного изменить, то получим следующий алгоритм.
Алгоритм 3 (модифицированный алгоритм Куна)
Вход: неориентированный двудольный граф 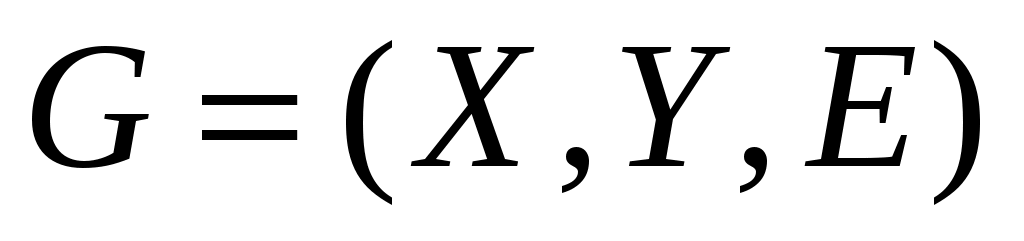
Выход: максимальное паросочетание
Метод:
function MAX_MATCHING_KHUN_MODIFIRED(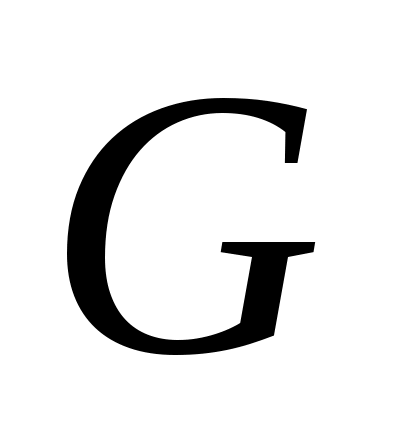 ) )
01(1)  := MAX_MATCHING_HEURISTIC( := MAX_MATCHING_HEURISTIC(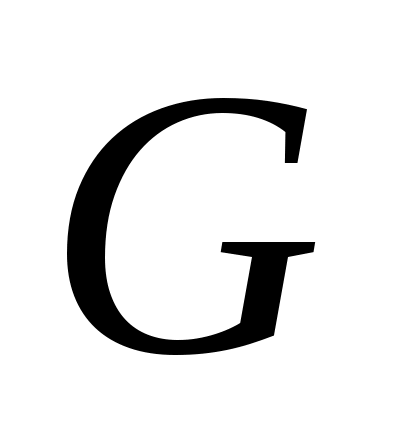 ) )
02 for 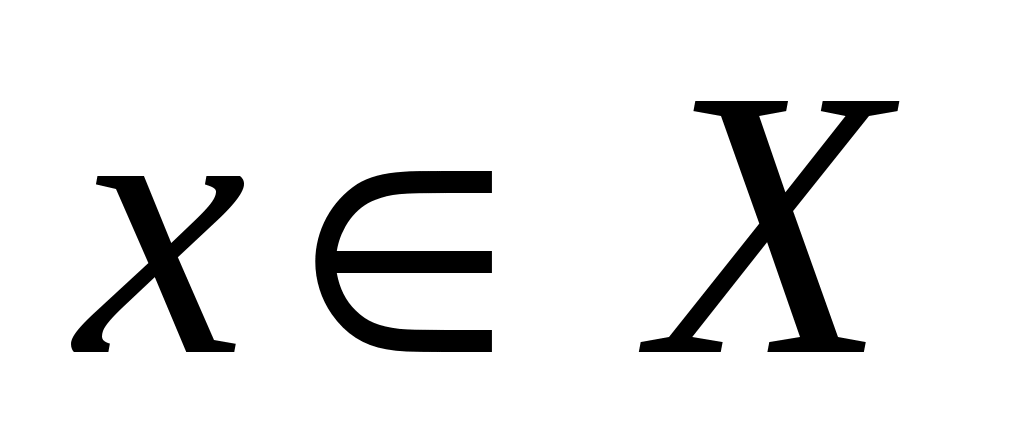 do do
03 Fill(used, FALSE)
04(1) if 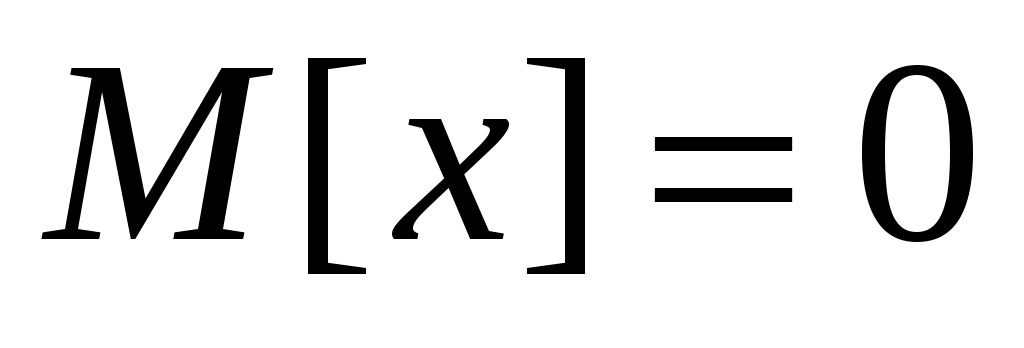 then then
04(2) TRY_KHUN( ) )
05 return 
end
|
Здесь подразумевается, что MAX_MATCHING_HEURISTIC(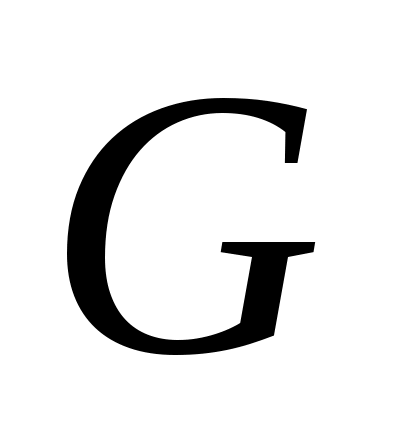 ) возвращает некоторое паросочетание (достаточно большое) найденное некоторым быстро работающим эвристическим методом. Примером такой функции может служить следующая функция. ) возвращает некоторое паросочетание (достаточно большое) найденное некоторым быстро работающим эвристическим методом. Примером такой функции может служить следующая функция.
Алгоритм 4 (эвристический алгоритм нахождения максимального паросочетания)
Вход: неориентированный двудольный граф 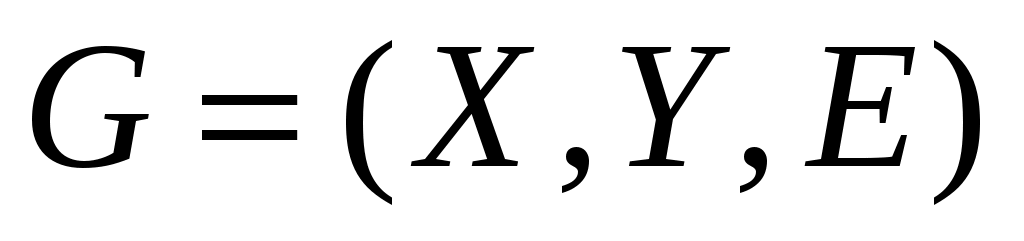
Выход: некоторое паросочетание
Метод:
function MAX_MATCHING_HEURISTIC(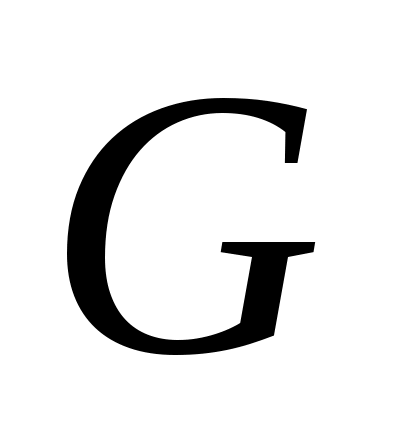 ) )
01  := := 
02 while в графе 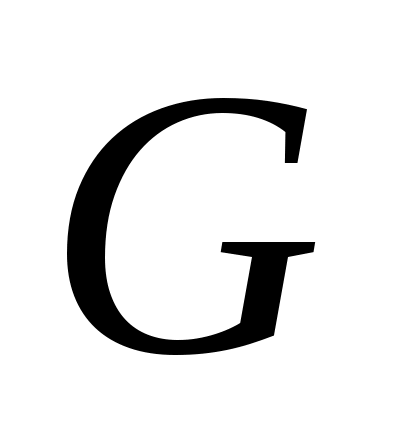 есть хотя бы одно ребро do есть хотя бы одно ребро do
03 найти неизолированную вершину 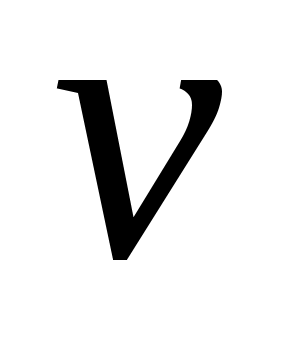
наименьшей степени
04 найти любое ребро 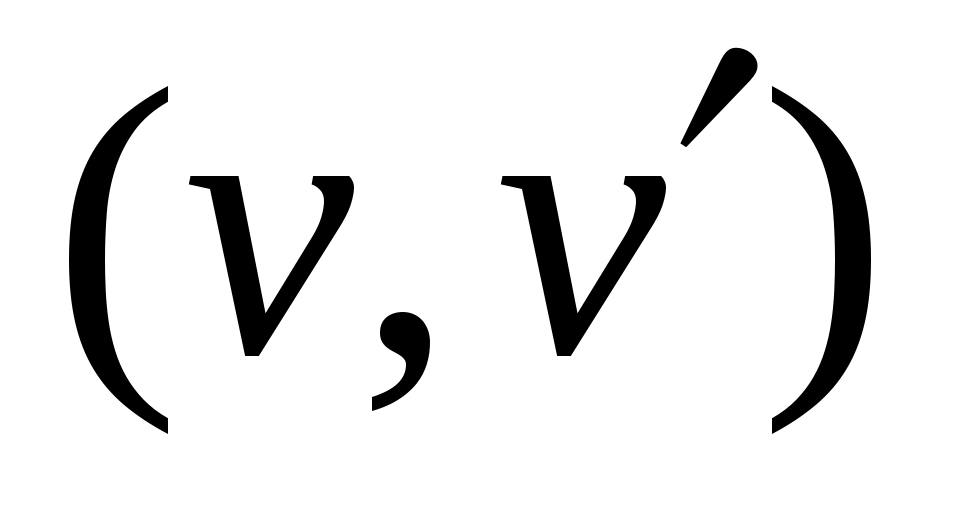 в графе в графе 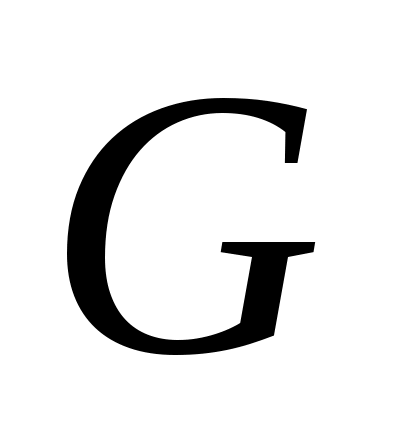
05  := := 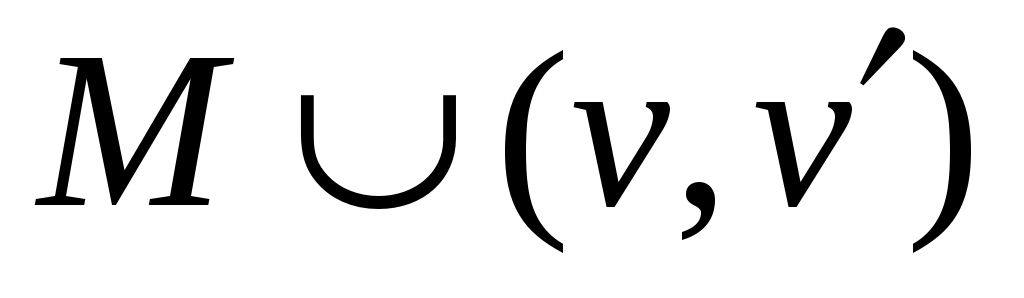
06 удалить из 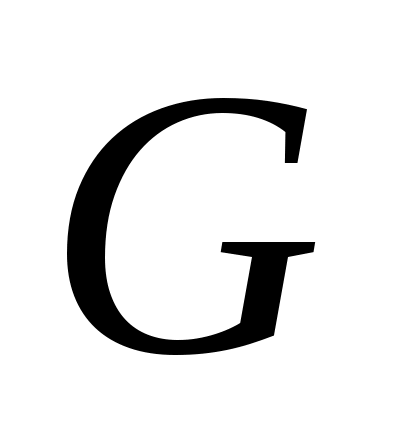 вершины вершины 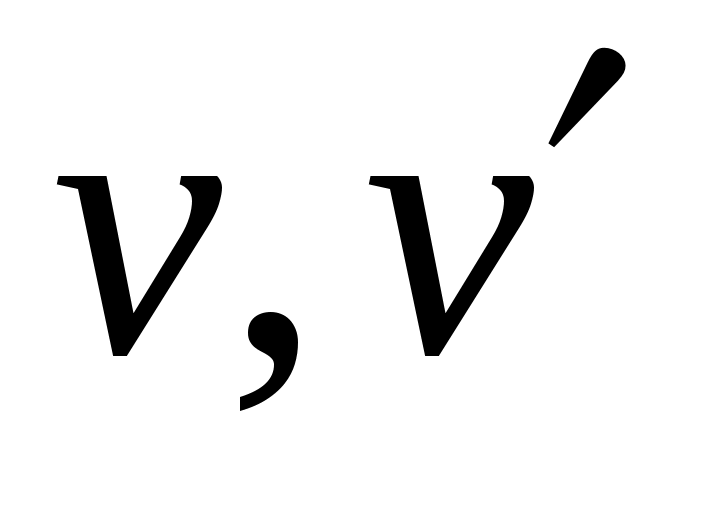
вместе с инцидентными ребрами
07 return 
end
|
Этот эвристический метод при использовании приведенной матрицы смежности легко реализовать за время 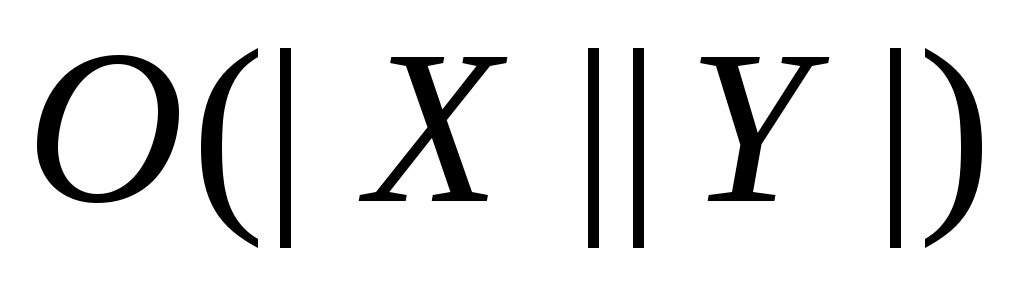 . На самом деле, его можно реализовать значительно эффективнее. Заметим, что алгоритм 4 дает отличные результаты на случайных графах и некоторых графах специального вида. . На самом деле, его можно реализовать значительно эффективнее. Заметим, что алгоритм 4 дает отличные результаты на случайных графах и некоторых графах специального вида.
На этом мы заканчиваем изучение вопросов связанных с алгоритмами построения максимального паросочетания, обойдя наиболее быстрый известный алгоритм Хопкрофта-Карпа, асимптотическая временная сложность которого составляет 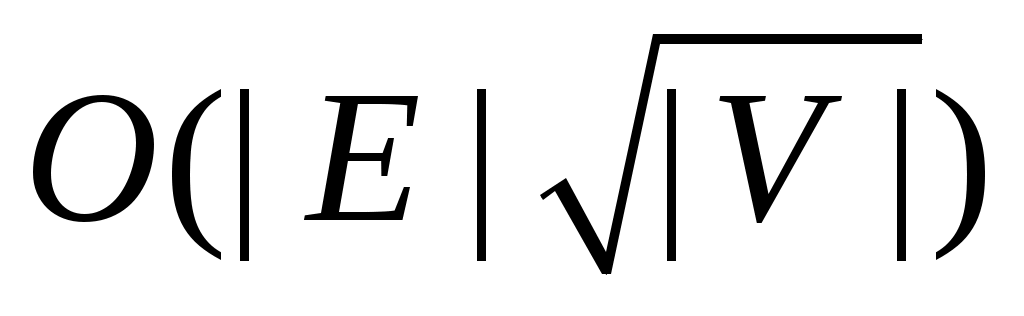 . .
|
 Скачать 1.13 Mb.
Скачать 1.13 Mb.



