техническая механика зачет. Механика. Основные законы классической механики
 Скачать 55.17 Kb. Скачать 55.17 Kb.
|
|
§ 3. Основные законы классической механики Классической механикой называется механика, построенная на трёх основных законах Галилея-Ньютона. Эти законы представляют собой результат обобщения выводов из многочисленных опытов и вековых наблюдений над движением тел. Практика подтверждает правильность следствий, вытекающих из этих законов. Построенные на основании законов классической механики сооружения прочны: машины работают, приборы действуют, корабли плавают, самолёты летают. Это служит неоспоримым доказательством правильности тех положений и законов механики, на основании которых они рассчитывались, доказательством того, что законы механики отражают объективные, не зависящие от сознания людей, процессы природы и, следовательно, сами являются объективными законами. Однако под законами механики нельзя понимать какие-то непреложные “вечные” истины. В силу несовершенства человеческого опыта они являются для нас лишь только определённым приближением к абсолютной истине. Положение диалектического материализма о том, что всякая настоящая наука содержит истины, лишь приближающиеся в соответствии с общим прогрессом к абсолютному познанию, остаётся, конечно, правильным и по отношению к механике. Успехи физики в начале нашего века показали, что законы классической механики не имеют неоспоримой ранее всеобщности и не применимы к движению макро частиц и к движению тел со скоростями, близкими к скорости света. Однако для целей обычной практики классическая механика (изучение основ которой и составляет содержание данного курса) полностью сохранила свое значение. Мы ограничимся пока рассмотрением двух (первого и третьего) основных законов механики и только в мере, необходимой для усвоения понятия о силе и изучение статики. В последнем разделе курса – динамике – мы дополним рассмотрение этих законов и подробно остановимся на втором основном законе механики, лежащем в основе динамики, но не имеющего отношения к статике. Первый закон (закон инерции). Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействия со стороны других тел не заставит его изменить это состояние. Тот факт, что тело при отсутствии действия на него со стороны других тел сохраняет состояние равномерного прямолинейного движения, противоречит, на первый взгляд, повседневному опыту и был открыт лишь в XVII веке Галилеем. Мы наблюдаем, что всякое тело, как будто бы предоставленное самому себе, постепенно уменьшает свою скорость и , наконец, останавливается. Однако, если глубже присмотреться к этому явлению, то станет ясным, что это кажущееся противоречие закону объясняется влиянием на движение данного тела других тел: трением тела о поверхность, по которой оно движется, сопротивлением воздуха и т. п. Они-то и замедляют движение тела. Если принять меры к уменьшению этих влияний(сопротивлений движению), то замедление будет меньшим и движение будет больше приближаться к равномерному. Отсюда можно заключить, что если бы нам удалость совершенно устранить все сопротивления движению тела, то скорость его не изменилась бы ни по направлению (следовательно, движение было бы прямолинейным), ни по численному значению (следовательно, движение было бы равномерным) . Для того чтобы поставить тело в такие условия, его нужно было изолировать, то есть так удалить от всех остальных материальных тел, чтобы на его движении не сказывалось их влияние. 1 Взаимодействие материальных тел, в результате которых происходит изменение скорости этих тел или их деформация, называется механическими. Мера механического действия на данное тело со стороны других тел, характеризующая величину и направление этого действия, называется силой, приложенной к данному телу. Практически нельзя, конечно, осуществить тело, совершенно изолированное от воздействия на него окружающих тел, то есть действия сил. Никаким способом нельзя полностью устранить силы сопротивления движению тела. Поэтому практически для поддержания движения тела к нему действительно нужно приложить силу. Если эта сила будет меньше силы сопротивления, то движение тела будет замедляться и тело остановится. Если она будет больше силы сопротивления, то скорость тела будет увеличиваться. Если же величина будет как раз равна величине силы сопротивления (а направление противоположно), то скорость тела будет сохраняться неизменной. В этом случае говорят, что приложенные к телу силы взаимно уравновешиваются или, видно, не влияют на движение тела, и, следовательно, их можно не учитывать при определении движения тела. Из сказанного можно сделать следующее: всякое тело, находящееся под действием взаимно уравновешенных сил, сохраняет свою скорость неизменной (в частности, сохраняет состояние покоя). Подобное тело можно рассматривать как тело, к которому силы не приложены вообще. Справедливо и обратное положение. Если какое-либо тело движется с неизменной скоростью, то все действующие на него силы взаимно уравновешиваются. Напротив, в случае изменения скорости тела можно утверждать, что действующие на него силы не находятся в равновесии. Сохранение телом состояния своего движения (численного значения и направления своей скорости и, в частности, состояния покоя) неизменным при отсутствии действия на него сил (или при их равновесии) называется инерцией тела. Отсюда и закон, устанавливающий это свойство всякого материального тела, получил название закона инерции. В древности считали покой естественным состоянием материи, полагая, что всякое тело, будучи выведено из состояния покоя, стремится к нему возвратиться. В переводе с латинского слово “инерция” означает косность, бездействие. Ясно, что в механике настоящее время это слово надо понимать иначе. Смысл понятия “инерция тела” простой и очевидный: движение тела не может измениться “само по себе”, без действия сил. Но достаточно приложить к любому телу любую, даже ничтожную малую силу, как оно тотчас же начнет изменять свою скорость и это изменение будет происходить все время, пока на тело действует сила. Третий закон (закон равенства действий и противодействия). Силы, с которыми действуют друг на друга два тела, всегда равны по численному значению и направлены по одной прямой в противоположные стороны. Все тела в природе находятся во взаимной связи и, следовательно, воздействуют друг на друга. Согласно третьему закону, действия тел друг на друга не бывают односторонними. Так, если тело притягивается к Земле, то оно само с такой же силой притягивает с себе Землю. Если тело испытывает сопротивление среды, то оно само с такой же силой действует на среду, вызывая в ней перемещение её частиц. При трении тела о плоскость одинаково трутся обе соприкасающиеся поверхности. Называя одну какую-либо их этих сил действием, другую мы считаем противодействием. Нужно твёрдо усвоить, что в природе не бывает одностороннего движения сил, а есть только взаимодействие тел. Все силы – силы парные. Поэтому, если мы и употребляем 2 часто такое выражение, как “к телу приложена сила”, то его надо понимать в том смысле, что с данной силой действует на рассматриваемое тело некоторое другое тело. При этом на последнее, в своею очередь, непременно действует данное тело с силой, равной первой по численному значению и противоположной по направлению. Интересуясь движением одного какого-либо тела, мы лишь оставляем в стороне вопрос о его обратном действии на другие тела, служащие источником приложенных к данному телу сил. Силы взаимодействия двух тел, хотя они и равны по численному значению и направлены по одной прямой в противоположные стороны, не уравновешивают друг друга, та как они приложены не к одному, а к двум различным телам. Если бы действие и противодействие уравновешивались, то никогда нельзя было бы давлением одного тела привести в движение другое, что, очевидно, неверно. Равенство “действия” и “противодействия” о котором говорится в третьем законе, нельзя смешивать с равенством их результатов. Результат действия какой-либо силы на тело определяется не только её величиной, но и совокупностью целого ряда обстоятельств: массой тела, его упругими свойствами и наличием других сил, действующих на данное тело. При столкновении, скажем, океанского парохода со шлюпкой, действия их друг на друга будут совершенно одинаковыми, результат же этих действий, конечно, будет различным. § 4. Понятие силы Понятие силы возникает из повседневного опыта. С первых же шагов своей жизни человек приобретает ощущение мускульного усилия, необходимого для того, чтоб поднять его, изменить его скорость и т. п. По аналогии с этим ощущением мы и называем силой всякое действие одного тела на другое, в результате которого тело изменяет свое механическое состояние. В окружающей нас действительности мы встречаемся с различными силами: силой тяжести, силой притяжения и отталкивания наэлектризованных и намагниченных тел, силой трения, силой давления одного тела на другое и т. д. Вопрос, почему возникают те или иные силы, являются предметом различных отделов физики, в теоретической же механике интересуются лишь их механическим эффектом, то есть производимым силами изменением механического состояния данного тела. Если изменения механического состояния тела выражается в изменении его скорости, то мы имеем, как иногда говорят, динамическое проявление силы. Так, например, под влиянием силы тяжести тело, брошенное вертикально вверх, постепенно уменьшает свою скорость и, наоборот, падающее тело увеличивает свою скорость. Если тело брошено под углом к горизонту, то под действием той же силы скорость тела изменяется и по численному значению и по направлению (тело в пустоте движется по параболе). Если же изменение механического состояния тела выражается не в изменении его скорости, а в деформации, то мы имеем, как говорят, статическое проявление силы. Так, например, силы тяжести тела не изменяет его движения, если тело лежит на столе. В этом случае тело взаимодействует ещё и со столом и сила тяжести тела, тянущая его вниз, уравновешивается силой сопротивления стола. Очевидно, что подобное действие стола на тело мы могли бы заметить мускульным усилием, поддерживая тело в том же положении рукой. Чем больше будет вес тела, а следовательно, и давление на руку, тем большее усилие потребуется от нас для его поддержания. Так как действие стола на лежащее на нём тело одинаково с действием нашего мускульного усилия, то по аналогии мы должны будем сказать, что с увеличением 3 силы давления на стол будет увеличиваться и сила противодействия стола. Вспомним, что абсолютно твёрдых тел не существует. Всякое реальное твёрдое тело в той или иной степени подобно пружине. Под действием внешних сил тело деформируется и в нём, как и в пружине, возникают силы упругости, сопротивляющиеся изменению его формы. Поведению стола легко дать объяснение, если заменить его мысленно пружиной. Чем больше давление тела, тем больше деформация крышки стола, тем больше возникающее в ней, как и в деформированной (сжатой) пружине, силы упругости, а следовательно, и обратное давление стола (пружины) на тело. Тело, производящее давление, в свою очередь также всегда деформируется. Представление об этом можно составить себе по отчётливому изменению поверхности руки при нажатии ею на что-либо, хотя бы на стол, и заметному напряжению при этом мускулов вследствие их сокращения. Установленные из опыта, из наблюдений за движением реальных физических тел, основные законы механики распространяются в теоретической механике и абсолютно твёрдые тела. Но ясно, например, что нарисованная выше картина взаимодействия стола и лежащего на нём тела теряет свой физический смысл, если стол считать абсолютно твёрдым. Такой стол не будет деформироваться вообще, а следовательно, и не может “реагировать” на изменение производимого на него давления. В применении к абсолютно твёрдым телам силы, возникающие при их непосредственном соприкосновении, становится такими же условными (но не произвольными) абстрактными понятиями , как и само абсолютно твёрдое тело. Как известно из опыта, действие силы на тело определяется следующими тремя элементами: 1) точкой приложения силы, 2) направлением силы и 3) численным значением (модулем) силы. Точкой приложения силы называется та материальная частица силы, к которой сила непосредственно приложена. Заметим, что понятие точки приложения силы условно, так как приложить силу в одной геометрической точке (не имеющей размеров) практически невозможно. Силы, которые мы в задачах механики рассматриваем как силы, сосредоточенные в одной точке, по существу представляют собой равнодействующую некоторой совокупности сил, действующих на все точки данной части поверхности или данного объема тела. Направление силы есть направление того прямолинейного движения, которого данная силы сообщила бы точке ее приложения, если бы эта частица тела свободно и находилась до этого в покое. Так, например, сила тяжести тела направлена вертикально вниз, ибо по этому направлению подают все тела при отсутствии действия на них других тел. Прямая, по которой направлена сила, называется линией действия силы. Численное значение (модуль) силы находится путём её сравнения с некоторой другой силой, принимаемой за единицу. Приборы, служащие для статического сравнения и измерения сил, называются динамометрами (силомерами). Примером простейшего динамометра служат обыкновенные пружинные весы. Принцип действия такого динамометра основан на том, что до известных пределов деформация (растяжение) пружины пропорциональна силе, её вызывающей и исчезает до прекращения действия силы. За единицу илы в наиболее распространённой пока в практике так называемой технической системе единиц принимается килограмм (сокращённо кг), то есть вес народного эталона, приблизительно (с весьма большой точностью) равный весу одного кубического дециметра чистой воды при 4ºС над уровнем моря и на широте 45º. 4 В настоящее время у нас в СССР (и в России) и в ряде других стран вводится так называемая “Международная система единиц ” являющаяся универсальной системой единиц , охватывающей все отрасли науки, техники и народного хозяйства. В международной системе единиц за единиц силы принимается сила, называемая ньютоном (сокращённо - µ). Для сравнения ньютона со старой единицей силы – килограммом – заметим, что 1 кг = 9,80665 µ ≈ 9,81 µ или 1µ = 0, 101971 кг ≈ 0, 102 кг Нетрудно запомнить, что ньютон примерно в 10 раз меньше силы в 1 кг. Выбор новой международной единицы силы основан на так называемой динамической определении силы, почему и обоснование этого выбора мы дадим в динамике. §5. Скалярные и векторные величины Различают два ряда физических величин, существенно отличающихся друг от друга. Одни величины, как температура, время, масса, плотность, площадь, объём и т. д. вполне характеризуются – при выбранной единице меры – алгебраическими или арифметическими числами. Чтобы характеризовать, скажем, в некоторый момент времени температуру воздуха в данном месте, достаточно измерить её, например, в градусах Цельсия. Полученное число (положительное или отрицательное) даёт значение температуры. Величины, вполне определяемые одним своим численным значением, называются скалярными величинами или просто скалярными. Для характеристики же других величин указания одного их численного значения недостаточно, нужно знать ещё и их направление. Величины, определяемые не только своим численным значением, но и направлением в пространстве, называются векторными величинами или просто векторными. К векторам относится не только сила, но и ряд других механических величин: скорость, ускорение и т. д. Всякая векторная величина графически изображается прямолинейным отрезком АВ, длина которогов выбранном масштабе советует численному значению вектора, а направление совпадает с направлением вектора. На чертеже это направление указывается стрелкой. Численная величина вектора называется его модулем. Модуль вектора есть положительная скалярная величина, то есть выражается арифметическим числом. Концы А и В отрезка АВ), изображающего вектор, называются соответственно началом и концом вектора АВ. Так как действия над векторами существенно отличаются от действий над скалярными величинами, то для отличия мы будем все векторные величины обозначать одной жирной буквой, например Р, или одной буквой обычного шрифта (светло буквой), но с чёрточкой сверху, например Р. Иногда вектор обозначается двумя светлыми буквами с чёрточкой сверху, например АВ. При этом первая буква обозначает начало вектора, а вторая – его конец. Модуль вектора мы будем обозначать той же буквой, что и вектор, но светлой, или теми же двумя буквами, но без чёрточки. Так, например, буквой Р мы будем обозначать модуль вектора Р, буквами АВ – модуль вектора АВ. Различают между собой три типа векторных величин (векторов). Векторы, связанные – векторы, начало которых связно с определённой точкой пространства, то есть векторы, имеющие определённую точку приложения. Векторы скользящие – векторы, за начало которых может быть принята любая. 5 точка, лежащая на некоторой прямой, имеющей направление данного вектора (линии его действия). Таким образом, скользящие векторы можно переносить вдоль их линий. Векторы свободные – векторы, за начало которых может быть принята любая точка пространства, то есть векторы, не связанные с определённой линией действия. Два свободных вектора называются равными, если они имеют одинаковые модули и одинаковые направления (то есть, если они параллельны и направлены в одну сторону). Так, например, векторы a и bт – равные векторы. Векторы же a и c, хотя они и имеют одинаковые модули, не равны, так как направления их различаются. В ромбе ABCD: AB=BC и BC=AD, но AB≠AD и AB≠DC. Равные векторы обычно не различают между собой обозначаю одинаково. Важно заметить, что в силу нельзя рассматривать как свободный вектор, ибо точку приложения силы нельзя выбрать произвольно. Над силами, так же как и над другими векторами, модно производить различного рода математические операции. Правила этих операций мы будем излагать в тех местах нашего курса, где это будет необходимо для понимания соответствующих положений механики и лишь в требуемом для этого объёме. В заключении данного параграфа скажем ещё несколько слов о масштабах вектора. Всякую векторную величину, как говорилось выше, принято графически изображать в виде прямолинейного отрезка определённой длины и определённого направления. Длина этого отрезка должна в каком-то масштабе отражать численное значение (модуль) вектора, природа и размеренность которого может быть любой. Поэтому обычный чертёжный масштаб для изображения векторов, вообще говоря, не применим. Если какая-нибудь векторная величина Q изображается на чертеже отрезком длины l, то масштабом µ этой величины будет: µ= 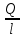 Из этой формулы следует, что размеренность масштаба вектора получается делением размеренности модуля (Q) вектора на размеренность длины (l). Масштаб µ обычно снабжается индексом, указывающим, к какой величине он относится. Если, например, требуется графически изобразить силу Р=200кг отрезком длины l=10мм, то масштаб силы будет равен 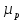 =20 кг/мм, для скорости v=20м/сек, изображаемой отрезком l=10мм, масштабом будет =20 кг/мм, для скорости v=20м/сек, изображаемой отрезком l=10мм, масштабом будет  =2 =2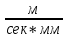 и т.п. и т.п.6 РАЗДЕЛ I СТАТИКА ГЛАВА I ВВЕДЕНИЕ В СТАТИКУ §6. Предмет и аксисом статики Статикой, как уже говорилось во введении, называется раздел теоретической механики, изучающий правила сложения сил и условия равновесия материальных тел, то есть те условия, при которых приложенные к телу силы не изменяют его движения. В этом случае абсолютно твёрдое тело как бы не испытывает на себе никакого действия и, следовательно, движется по инерции. Таким образом, под равновесием тела надо понимать, вообще, его движение по инерции, а не только состояние покоя. В основании статики, помимо первого и третьего основных законов классической механики, лежит ещё несколько подтверждаемых многовековой практикой положений , называемых аксиомами статики. Опираясь на них, логическим путём строятся все остальные положения статики. Условимся предварительно о следующих определениях. Совокупность сил, действующих на данное тело, называется системой сил. Силы, входящие в состав данной системы, называются составляющими этой системы. Если система сил такова, что под действием свободное тело не изменяет своего равномерного движения или, в частности, продолжает оставаться в покое, то такая система сил называется уравновешенной системой. Про силы такой системы говорят, что они находятся в равновесии. Под “свободным” телом понимается тело, не скреплённое с другими телами, то есть тело, которому можно сообщить любое перемещение в пространстве. Правила этих операций мы будем излагать в тех местах нашего курса, где это будет необходимо для понимания соответствующих положений механики и лишь в требуемом для этого объёме. Сила, которая будучи присоединена к некоторой системе сил, действующих на тело, приводит систему к равновесию, называется уравновешивающей данной системе сил. Очевидно, что в уравновешенной системе каждая из сил является уравновешивающей по отношению ко всем остальным Две системы сил называются эквивалентными, если они оказывают одинаковое механическое действие на одно и то же свободное твёрдое тело. Одна сила, эквивалентная данной системе сил, называется равнодействующей этой системы. Силы, действующие на данное тело со стороны других тел, называется внешними силами. Силы взаимодействия между частицами данного тела называются внутренними силами. Первая аксиома. Абсолютно твёрдое тело находящееся в равновесии под действием двух сил тогда и только тогда, когда эти силы равны по модулю и направлены по одной прямой в противоположные стороны. Необходимо иметь ввиду, что данная аксиома, как и все вообще положения статики, безоговорочно применима только к абсолютно твёрдому телу. При применении же её к реальным деформируемым телам необходимо учитывать особенности этих сил. Если например мы приложим две равные по модулю и противоположные по направлению 7 силы 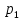 и и 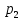 к концам гибкой нити, то она будет находится в равновесии только при сборе приложения этих сил, показанном на (когда нить растягивается). к концам гибкой нити, то она будет находится в равновесии только при сборе приложения этих сил, показанном на (когда нить растягивается).При способе же приложения этих сил, показанном на (нить сжимается),нить сомнётся и не будет находиться в равновесии. Если же вместо нити мы возьмём твёрдый стержень, то в обоих случаях, изображённый на, он будет находиться в равновесии. Вторая аксиома. Не нарушая действия данной системы сил на абсолютно твёрдое тело, можно добавить к этой системе сил или отнять от неё любую уравновешенную систему сил. Другими словами, присоединяя к данной системе сил, действующих на твёрдое тело, любую уравновешенную систему сил, мы получаем систему, эквивалентную данной. Наоборот, если в состав данной системы входит несколько сил, образующих в отдельности уравновешенную группу, то можно отбросить такую группу сил. оставшаяся система эквивалента данной. Следствие первое. Всякую силу, приложенную в какой-либо точке абсолютно твёрдого тела, можно, не изменяя её действия, переносить в любую другую точку, лежащую на линии действия этой силы. Доказательство. Пусть на тело действует сила Р, приложенная в точке А. Возьмём на линии действия какую-нибудь произвольную току В и приложим к ней две силы 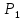 и и 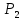 , численно равные силе Р (так что модули их Р= , численно равные силе Р (так что модули их Р=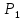 = =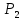 ) и действующие по одной с ней прямой АВ в противоположные стороны. Силы, ) и действующие по одной с ней прямой АВ в противоположные стороны. Силы, 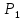 и и 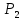 численно равны и направленны противоположно. По первой аксиоме статики они взаимно уравновешиваются; следовательно, на основании второй аксиомы от их присоединения состояние абсолютно твёрдого тело не изменится. Но силы Р и численно равны и направленны противоположно. По первой аксиоме статики они взаимно уравновешиваются; следовательно, на основании второй аксиомы от их присоединения состояние абсолютно твёрдого тело не изменится. Но силы Р и 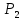 также взаимно уравновешиваются (на основании первой аксиомы), и их поэтому можно отбросить, не изменяя состояния абсолютно твёрдого тела остаётся лишь одна также взаимно уравновешиваются (на основании первой аксиомы), и их поэтому можно отбросить, не изменяя состояния абсолютно твёрдого тела остаётся лишь одна 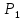 ,равная данной силе Р и лежащая на линии её действия. Так точка приложения силы ,равная данной силе Р и лежащая на линии её действия. Так точка приложения силы 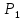 (точка В) была выбрана на линии действия данной силы произвольно, то следствие доказано. (точка В) была выбрана на линии действия данной силы произвольно, то следствие доказано.Мы видим, что для абсолютно твёрдого тела точка приложения перестаёт быть существенным элементом силы, её заменяет линия действия силы. Вспоминая сказанное и типах векторов, можно заметить, что по отношению к абсолютно твёрдому телу сила является скользящим вектором. Таким образом, действие силы на абсолютно твёрдое тело определяется следующими элементами 1) модулем, 2)линией действия и 3)направлением силы по линии её действия. Конечно в каждом отдельном случае можно приписать силе и некую точку приложения, но эта точка всегда может быть заменена другой точкой, лежащей на линии действия силы. Необходимо заметить, что присоединение и отбрасывание уравновешенных сил, так же как и перенос силы вдоль линии её действия, изменяет картину распределения внутренних сил в теле. Так, например, изменение расположения сил, приложенных к концам стержня, может быть получено путём переноса сил 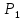 и и 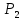 вдоль их линий действия в соответственно противоположные концы стержня. Ясно, что такой перенос с случае деформируемого стержня существенно изменяет его внутреннее состояние, так как в первом случае м=стержень растягивается, а во втором – сжимается. вдоль их линий действия в соответственно противоположные концы стержня. Ясно, что такой перенос с случае деформируемого стержня существенно изменяет его внутреннее состояние, так как в первом случае м=стержень растягивается, а во втором – сжимается.В применении к реальным физическим телам данными приёмами можно пользоваться только тогда, когда рассматривается лишь внешнее действие сил на данное тело, то есть когда определяется лишь общие условия равновесия этого тела. При рассмотрении этих условий мы принимаем тело на абсолютно твёрдое и внутренние силы можно вообще не принимать во внимание. В самом деле, по закону равенства действия и противодействия любые две частицы тела действуют друг на друга с силами, равными по модулю и 8 направленными по одной прямой в противоположны стороны. Следовательно, в своей совокупности эти силы всегда представляют уравновешенную систему и в случае абсолютно твёрдого тела и их можно отбросить. Так как в статике рассматривается равновесие именно абсолютно твёрдых тел, то в дальнейшей под силами, действующими на тело, мы всегда будем понимать только внешние силы (если не будет сделано специальной оговорки). Следствие второе. Равнодействующая и уравновешивающаяся силы равны по модулю и направлены по одной прямой в противоположные стороны. Доказательство. Положим, что сила R есть равнодействующая сил 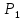 , , 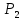 … …  . Приложим по линии действия равнодействующей равную ей по модулю, но направленную в противоположную сторону силу . Приложим по линии действия равнодействующей равную ей по модулю, но направленную в противоположную сторону силу 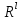 . Как силы, равные по модулю и противоположно направленные, силы R и . Как силы, равные по модулю и противоположно направленные, силы R и 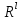 взаимно уравновешиваются. Не нарушая составляющими, то есть эквивалентной ей системой сил взаимно уравновешиваются. Не нарушая составляющими, то есть эквивалентной ей системой сил 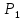 , ,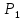 … …  . .Так как по условию сила 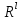 равна по модулю и направлена противоположно силе R, то требуемое положение доказано. Из данного следствия вытекает, что нахождение сил, уравновешивающей данную систему сил, можно свести к определению равнодействующей этой системы. равна по модулю и направлена противоположно силе R, то требуемое положение доказано. Из данного следствия вытекает, что нахождение сил, уравновешивающей данную систему сил, можно свести к определению равнодействующей этой системы.Третья аксиома. Равнодействующая двух сил, приложенных в одной точке, приложена в той же точке и изображается диагонально параллелограмма, построенного на данных силах, как на сторонах. Параллелограмм, построенный на данных силах, называется параллелограммом сил, а сам способ нахождения равнодействующей путём построения параллелограмма называется правилом параллелограмма. Сложение сил, как и других векторных величин, по правилу параллелограмма называют их геометрическим (векторным) сложением. Геометрическое сложение сил, как сложение любых векторов, обозначается обычным знаком сложения (+), стоящим между жирными буквами (или буквами с чёрточками над ними), обозначающими силы. Если обозначить через R равнодействующую двух сил 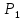 и и 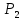 , приложенных к одной точке О тела, то на основании данной аксиомы имеем: , приложенных к одной точке О тела, то на основании данной аксиомы имеем:R= 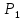 + + Нужно заметить, что понятие геометрической суммы сил, вообще говоря, не тождественно понятию равнодействующей. В случаях, когда силы приложены к различным точкам тела, геометрическая сумма сил, как мы увидим дальше, не вполне определяет их равнодействующую. Более того, в отдельных случаях система сил может и не иметь равно действие вовсе. Третья аксиома статики говорит о равнодействующей двух сил, приложенных в одной точке. Если две силы приложены в различных точках тела, но линии их действия пресекаются, то, пользуясь следствием 1, мы можем перенести обе силы в точку пересечения их линий действия и затем сложить по правилу параллелограмма. Если линии действия сил пересекаются где-либо вне тела, то перенося обе силы в их точку пересечения и определив равнодействующую, нужно затем перенести её по линии действия в одну из точек тела. Четвёртая аксиома (принцип отвердевания). Если нетвёрдое тело находится в равновесии, то это равновесие не нарушится и в том случае, если тело станет абсолютно твёрдым. Аксиома очевидна, так как превращение находящегося в равновесии тела (то есть тела с подвижными частицами) в абсолютно твёрдое тело (то есть с неподвижными частицами) может только ещё более ограничивать возможные движения тела, только ещё более 9 закреплять равновесие тела, а не нарушать его. Принцип отвердевания позволяет применять к любому нетвёрдому телу и к любой изменяемой конструкции условия равновесия, устанавливаемые статикой для абсолютно твёрдого тела. Эти условия являются необходимыми условиями равновесия и для нетвёрдых тел, но не всегда достаточными. Как мы уже говорили выше, для равновесия гибкой нити недостаточно того, чтобы приложенные к её концам силы были равны по модулю и направлены по одной прямой в противоположны стороны, нужно ещё чтобы они растягивали нить, а не сжимали. Таким образом, учёт деформаций, возникающих в реальном теле под действием приложенных к нему сил, лишь дополняет результаты, полученные в механике абсолютно твёрдого тела, но не уничтожает их. § 7. Связи и реакции связей. При решении большинства задач механики приходится иметь дело с телами несвободными, то есть с такими, которые соприкасаются или скреплены с другими телами, благодаря чему становятся невозможными те или иные перемещения данного тела. Если тело несвободно, то говорят, что на него наложены связи. Связями называются тела, ограничивающие свободу перемещения данного тела. Так, как для, лежащего на столе, связью является стол, для вала, лежащего в подшипниках, связями являются подшипники, для лестницы, приставленной к стене, связями являются стена и пол. Если под действием приложенных к нему сил тело будет давить на связь, то связь, в свою очередь, будет действовать на данное тело. Сила, с которой связь действует на тело, препятствуя его перемещению в том или ином направлении, называется силой реакции (противодействия) этой связи. По закону равенства действия и противодействия сила реакции связи равна по модулю силе давления на связь и направлена в сторону, противоположную этой силе, то есть в сторону, противоположную той, куда данная связь препятствует перемещаться телу. Реакции связей существует только тогда, когда данное тело действует на связи; как только прекращается это действие, перестают действовать и реакции. В этом отличие сил реакций от так называемых активных сил, модуль и направление которых не зависит от других действующих на тело сил. Активными силами являются все силы, не являющиеся силами реакции связей. Задачи на равновесие несвободных тел решаются в статике на основании следующего очевидного обстоятельства: всякое несвободное тело можно рассматривать как свободное, если мысленно освободить его от связей и заменить их действие на тело силами реакций этих связей (принцип освобождаемости или аксиома связей). Необходимо всегда помнить, что, освобождаясь от связей, наложенных на данное несвободное тело, и рассматривая приложенные к телу силы, нужно обязательно включить в их число и силы реакций отброшенных связей. Ввиду исключительной важности для решения практических задач умения находить реакции связей выясним их основные типы. Простейшая связь осуществляется поверхностью другого тела, препятствующей движению данного тела в определённом направлении. Эта поверхность может быть шероховатой или идеально гладкой, не создающей трения; в последнем случае связь называется идеальной. Рассмотрением таких идеальных связей мы 10 пока и ограничимся. Как мы уже говорили, направление реакции связи всегда противоположно тому направлению, по которому данная связь мешает перемещаться телу. Так как абсолютно гладкая поверхность не препятствует скольжению по ней поверхности тела и препятствует лишь перемещению, направленному по нормали к этим поверхностям в точке их соприкосновения, то её реакция R направлена по этой нормали. Величина реакции равна давлению, производимому телом на поверхность, и зависит от активных сил, приложенных к телу. Итак, гладкая поверхность всегда даёт одну нормальную реакцию, то есть реакцию, направленную по общей нормали к поверхности данного тела и к поверхности связи в их точке касания. Проведение общей нормали в точке соприкосновения двух поверхностей обычно затруднений не представляет. Замети, что понятие об общей нормали теряет смысл в тех случаях, когда поверхность данного тела или поверхность связи имеет в месте касания заострение. Реакция связи должна быть направлена в этом случае по нормали к той поверхности, для которой её проведение является задачей определённой. Например, к гладкому брусу АВ, опирающемуся к точке А на пол и в точке В на столб, приложены реакции пола 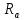 и столба и столба 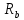 . Если бы это реакции были направлены как-нибудь иначе, то их всегда можно было бы разложить на составляющие. Но так как гладкие поверхности не препятствуют скольжению по ним, то составляющие . Если бы это реакции были направлены как-нибудь иначе, то их всегда можно было бы разложить на составляющие. Но так как гладкие поверхности не препятствуют скольжению по ним, то составляющие 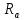 и и 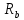 быть не может. быть не может.В некоторых случаях, однако, направление реакции связи заранее не может быть указано и определение его является задачей более сложной. Такова, например, весьма распространённая связь, осуществлённая при помощи неподвижного цилиндрического шарнира. На неподвижны цилиндрический болт-палец надевается втулка. Втулка имеет цилиндрическое отверстие, диаметр которого несколько больше диаметра болта. Тело, жёстко скреплённое с втулкой, очевидно, может только вращаться вокруг оси шарнира, перпендикулярной к плоскости. Во многих случаях можно пренебречь трением в шарнире (между поверхностями пальца и втулки). В таком шарнире (называемом “идеальным”) нет препятствий ни для поворота втулки вокруг оси болта, ни для её перемещения вдоль этой оси. Идеальный шарнир препятствует лишь перемещению втулки в направлении нормали к поверхностям, его реакция может быть направленной только по этой нормали (по радиусу болта). Но, так как втулка в зависимости от её расположения и приложенных к ней сил может прижиматься к любой точке болта, то указать заранее направление реакции неподвижного цилиндрического шарнира (даже если он “идеальный”) нельзя. Единство, что может утверждать (если пренебречь трением в шарнире), это то, что реакция неподвижного цилиндрического шарнира всегда направлена по нормалям к его поверхности, то есть что реакция лежит в плоскости, перпендикулярной к оси шарнира и имеет радиальное направление. Для определения реакции связи в тех случаях, её направление оказывается неопределённым, очень часто полезно заменить искомую реакцию двумя составляющими реакциями, неизвестными уже только по величине. Линии действия составляющих реакций могут быть выбраны при этом произвольно, но чаще всего неизвестную реакцию разлагают на горизонтальную и вертикальную составляющие. Например, реакции неподвижного шарнира или упора А удобно разложить на горизонтальную 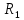 и вертикальную и вертикальную 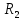 составляющие. В обоих случаях можно считать, что связь А (шарнир или упор) препятствует телу перемещаться как в горизонтальном, так и в вертикальном составляющие. В обоих случаях можно считать, что связь А (шарнир или упор) препятствует телу перемещаться как в горизонтальном, так и в вертикальном 11 направлениях. После того как будет найдены модуль и направление каждой из составляющих реакций, может быть (при необходимости) найдена и полная реакция связи, как равнодействующая её составляющих. Заметим, что, разлагая реакцию на составляющие (в данных примерах на горизонтальную и вертикальную), можно не заботиться о правильности выбора направления по намеченным линиям их действия (вправо или влево, вверх или вниз). В случае, если в действительности та или иная составляющая должна быть направленной в сторону противоположную взятой нами, то мы будем получать для неё в ответе отрицательное значение. Неподвижный шарнир представляет собой так называемую шарнирно-неподвижную опору. Такая опора часто схематически изображается двумя стержнями, соединёнными между собой на одном конце общим шарниров А, ось которого, очевидно, будет неподвижной. Реакция такой опоры проходит через ось шарнира, но неизвестна как по модулю, так и по направлению и , следовательно, характеризуется двумя неизвестными элементами. Определение модуля и направления реакции шарнирно-неподвижной опоры можно, как было сказано выше, заменить определением модулей двух составляющих этой реакции. Наличие шарнирно-неподвижной опоры двух стержней как раз и указывает на неизвестность двух элементов реакции данной связи. Мы говорили до сих пор о связях, осуществлённых абсолютно гладкими поверхностями. Эти связи препятствуют перемещению тел только в направлении, перпендикулярном к поверхности, и характеризуются одной нормальной реакцией. Негладкая поверхность не только препятствует перемещению, нарушающему связь, но и затрудняет перемещение по самой поверхности. Следовательно, реакция негладкой поверхности имеет две составляющие: одну – нормальную к поверхности, и другую – лежащую в плоскости скольжений (в общем касательно плоскости к поверхности тела и опорной поверхности) и направленную в сторону, противоположную той, в которую двигают (или стремятся сдвинуть) тело приложенные к нему активные силы. Первая составляющая является нормальной реакцией, вторая носит название силы трения. Следовательно, негладкие опорные поверхности отличаются тем, что для них приходится дополнительно учитывать силу трения. О том, как это делается, мы будем говорить дальше, в главе о трении, а сейчас отметим только, что хотя идеально гладких поверхностей, а следовательно, и идеальных связей в действительности не существует, но во многих случаях практики величина силы трения может быть настолько малой, что можно пренебречь ею и практически считать связи идеальными. Примером такой связи является часто применяемая опора на катках. Подвижность катка настолько велика и, следовательно, сила трения настолько мала, что можно считать данную связь препятствующей лишь перемещению, перпендикулярному к опорной плоскости, почему она и характеризуется всегда лишь одной нормальной реакцией. Опора на катках не препятствует перемещению оси шарнира параллельно опорной плоскости и представляет собой так называемую шарнирно-подвижную опору. Такая опора часто схематически изображается одним стержнем, с шарнирами по концам. Реакция подобной опоры проходит через ось шарнира и направлена по нормали к опорной поверхности. наличие опоры одного стержня указывает на неизвестность лишь одного элемента реакции шарнирно-подвижной опоры – её модуля. Все рассмотренные нами до сих пор связи осуществлялись путём непосредственного соприкосновения поверхностей тел. Связью другого типа является связь, осуществлённая через промежуточные тела. Такой случай мы имеем, например, при подвешивании тела 12 посредством гибкой нити или цепи. Пусть к концу А нити АВ, другой конец которой непосредственно прикреплён к крюку В, подвешен груз весом G. По закону равенства действия и противодействия реакция нити 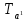 направлена вертикально вверх и численно равна весу груза G. Нетрудно сообразить, что к крюку В от нити приложены реакция нити направлена вертикально вверх и численно равна весу груза G. Нетрудно сообразить, что к крюку В от нити приложены реакция нити 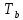 (равная по модулю G), если пренебречь весом нити; ей соответствует реакция крюка (равная по модулю G), если пренебречь весом нити; ей соответствует реакция крюка 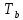 . Важно заметить, что нить оказывает равные по величине, но противоположные по направлению действия тела, с которыми она соприкасается своими концами, то есть, что . Важно заметить, что нить оказывает равные по величине, но противоположные по направлению действия тела, с которыми она соприкасается своими концами, то есть, что 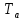 = =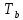 , если, разумеется, пренебречь весом нити. Модуль этой силы называют натяжением нити. , если, разумеется, пренебречь весом нити. Модуль этой силы называют натяжением нити.Если груз весом G подвешен на нитях, то в точке А будет приложены сила G, равная по модулю весу груза и растягивающая нити АВ и АС. Реакция этих нитей 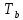 и и  , численно равные натяжениям, будут направлены вдоль нитей. , численно равные натяжениям, будут направлены вдоль нитей.Нити могут быть без изменения направлений реакций заменены твёрдыми стержнями при условии их невесомости и соединения посредством идеальных шарниров. Вследствие отсутствия трения в идеальных шарнирах приложенные к концам стержней силы всегда окажутся направленными вдоль этих стержней. Эти силы будут только растягивать или сжимать стержни. В самом деле, как мы знаем, идеальный шарнир характеризуется только одной нормальной реакцией. Но две силы, приложенные к стержню в его концах, могут уравновешиваться только тогда, когда они равны по величине, направлены противоположно и действуют по одной прямой, соединяющей их точки приложения. Следовательно, реакции невесомых шарнирно закреплённых и нагруженных по концам стержней всегда направлены вдоль прямой, соединяющей центры шарниров. Подобным же образом, очевидно, будут направлены и реакции шарнирно закреплённых стержней, подпирающих тело. 13 |
