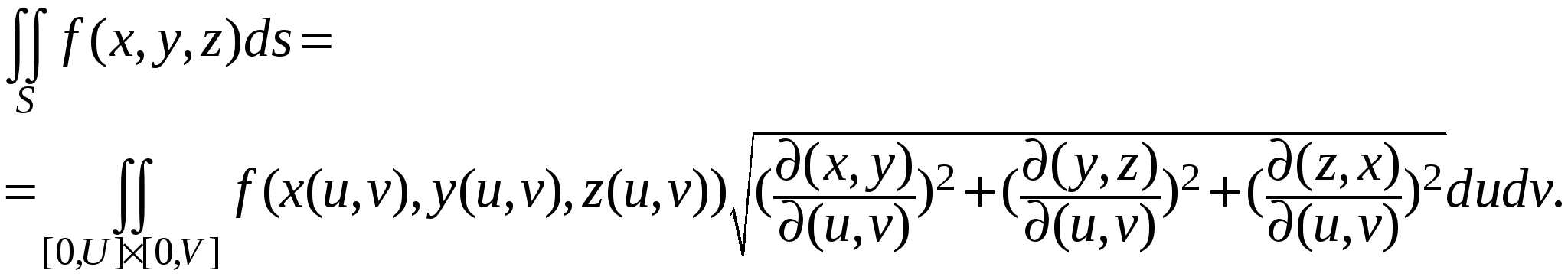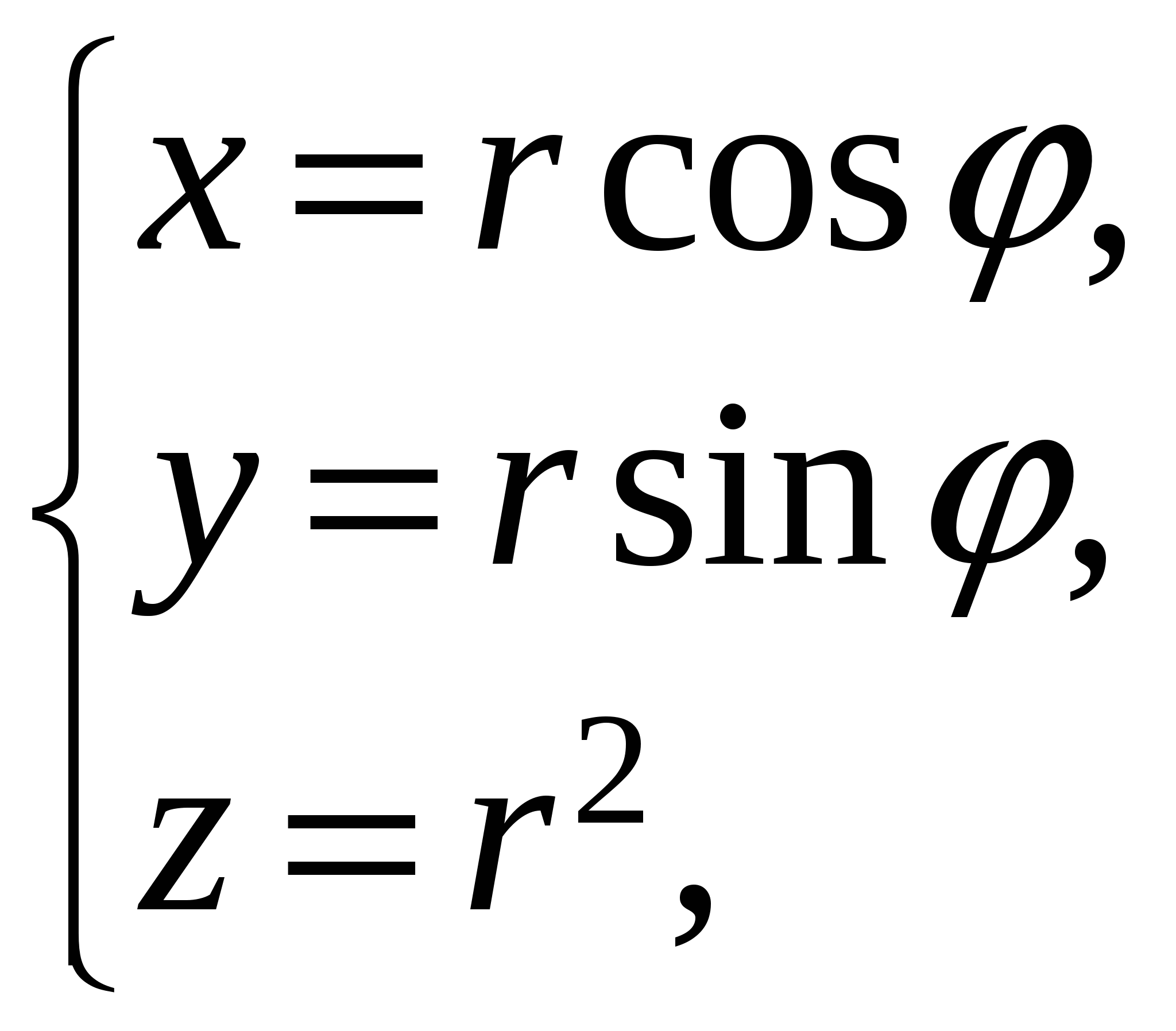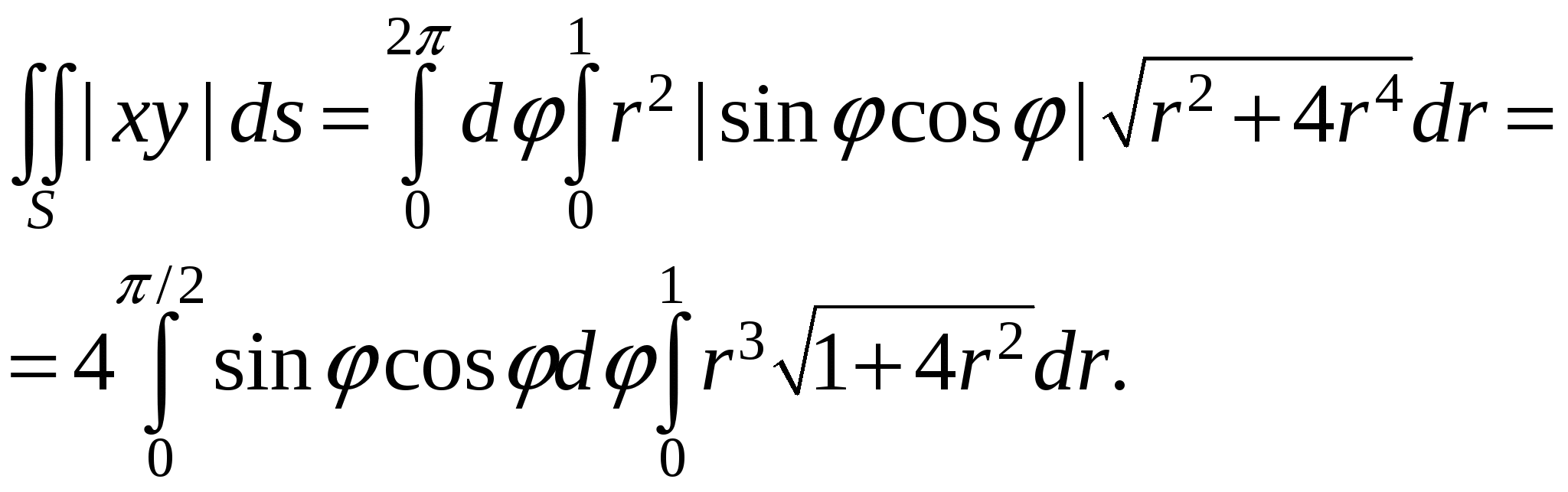Вычислить 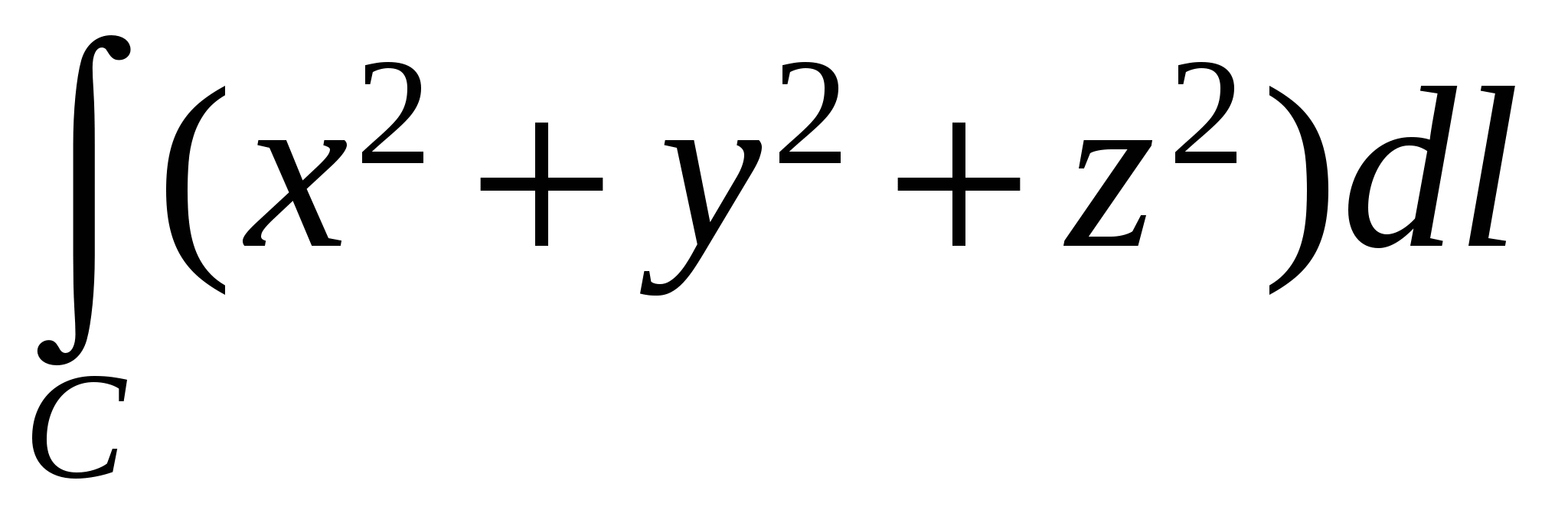 , где C – часть винтовой линии , где C – часть винтовой линии 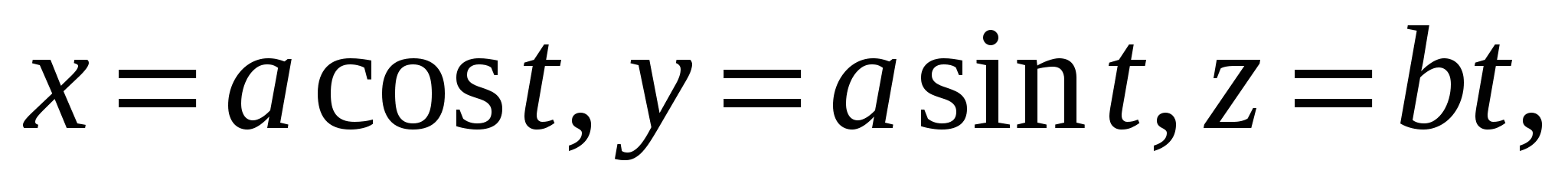 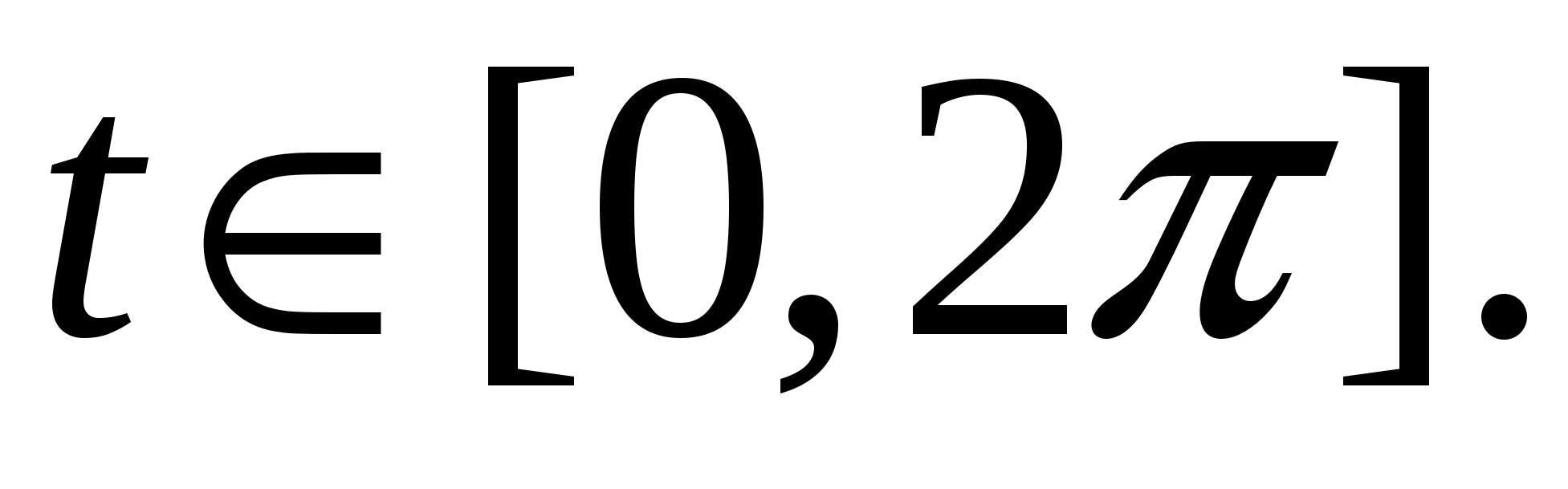
3. Найти массу дуги кривой 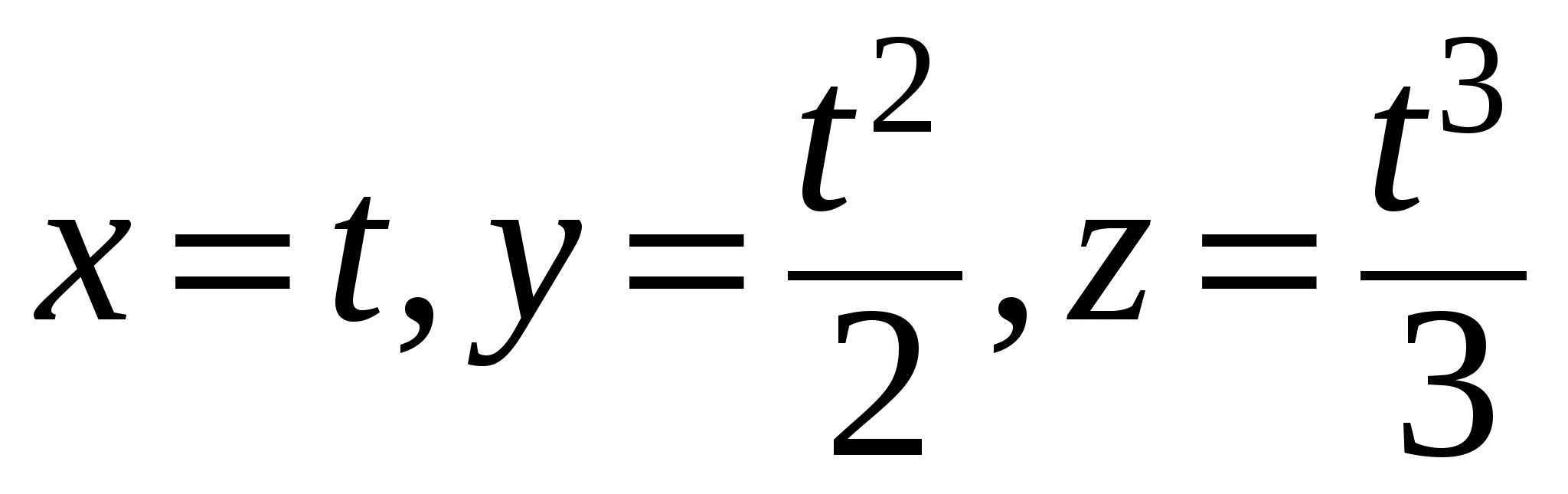 , , 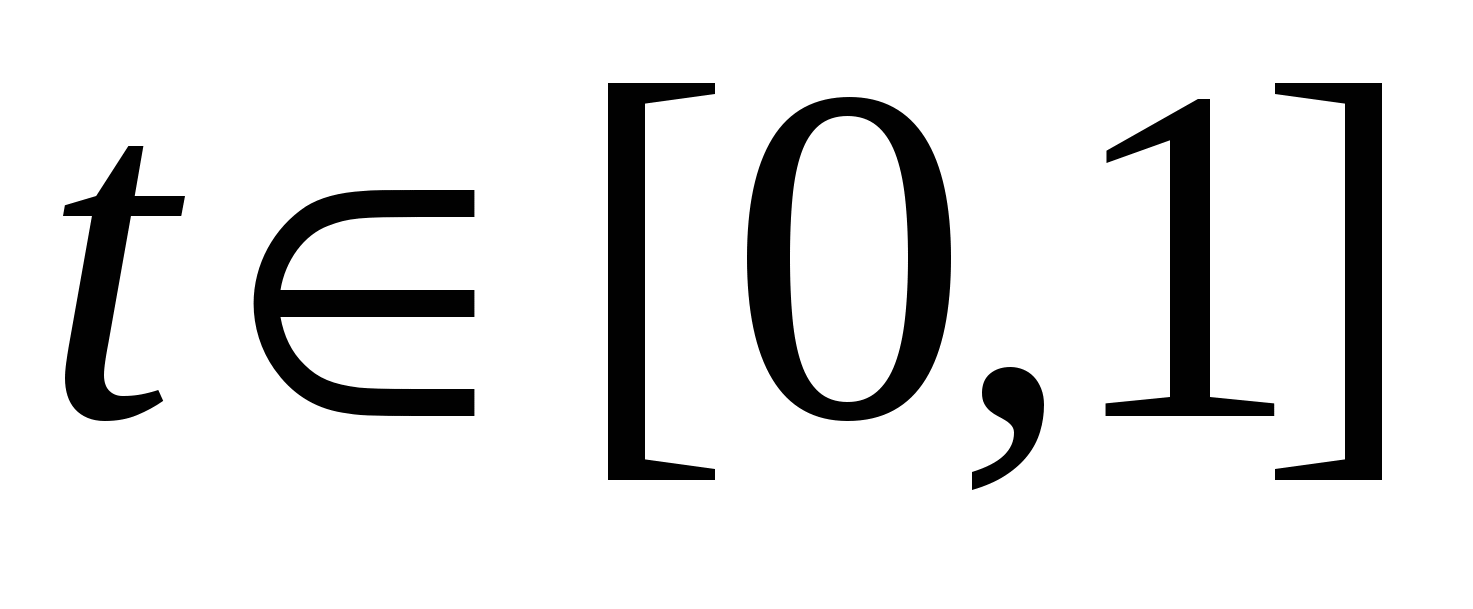 , плотность которой меняется по закону , плотность которой меняется по закону 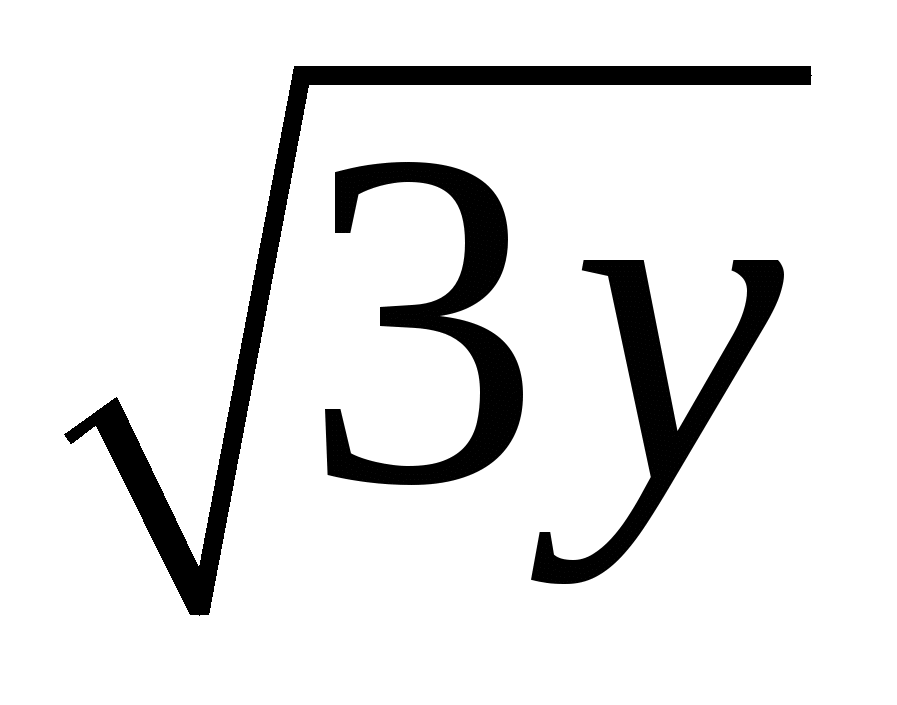 . .
2. Криволинейный интеграл второго рода.
Задача о вычислении работы силы вдоль кривой.
Пусть С – спрямляемая кривая в пространстве XYZ с заданным направлением движения по ней. В каждой точке кривой задан вектор силы
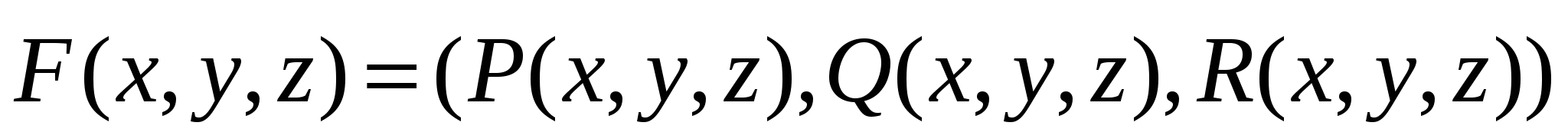 . .
Следует вычислить работу силы 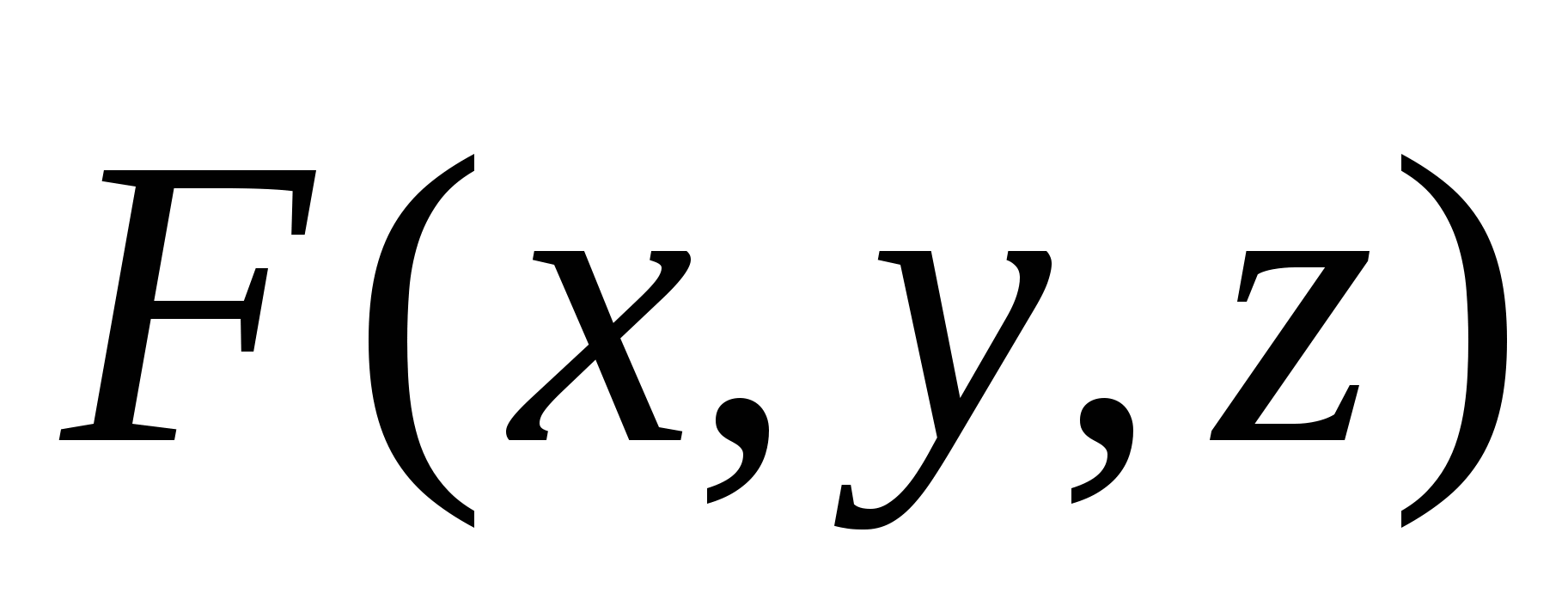 вдоль кривой C. вдоль кривой C.
Если бы кривая была прямолинейным направленным отрезком  , а сила , а сила 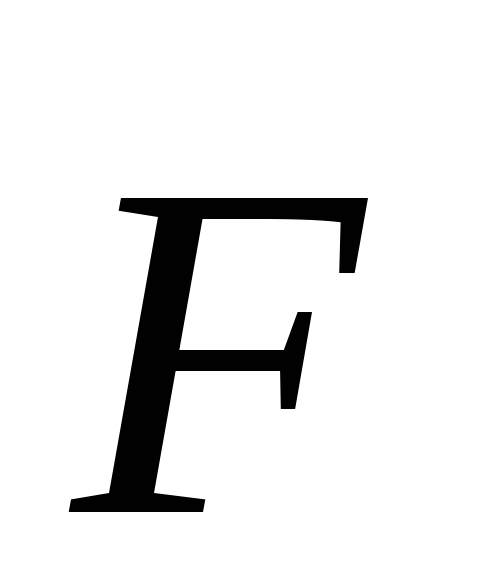 была постоянной вдоль всего этого отрезка, работу мы вычислили бы с помощью скалярного произведения по формуле была постоянной вдоль всего этого отрезка, работу мы вычислили бы с помощью скалярного произведения по формуле 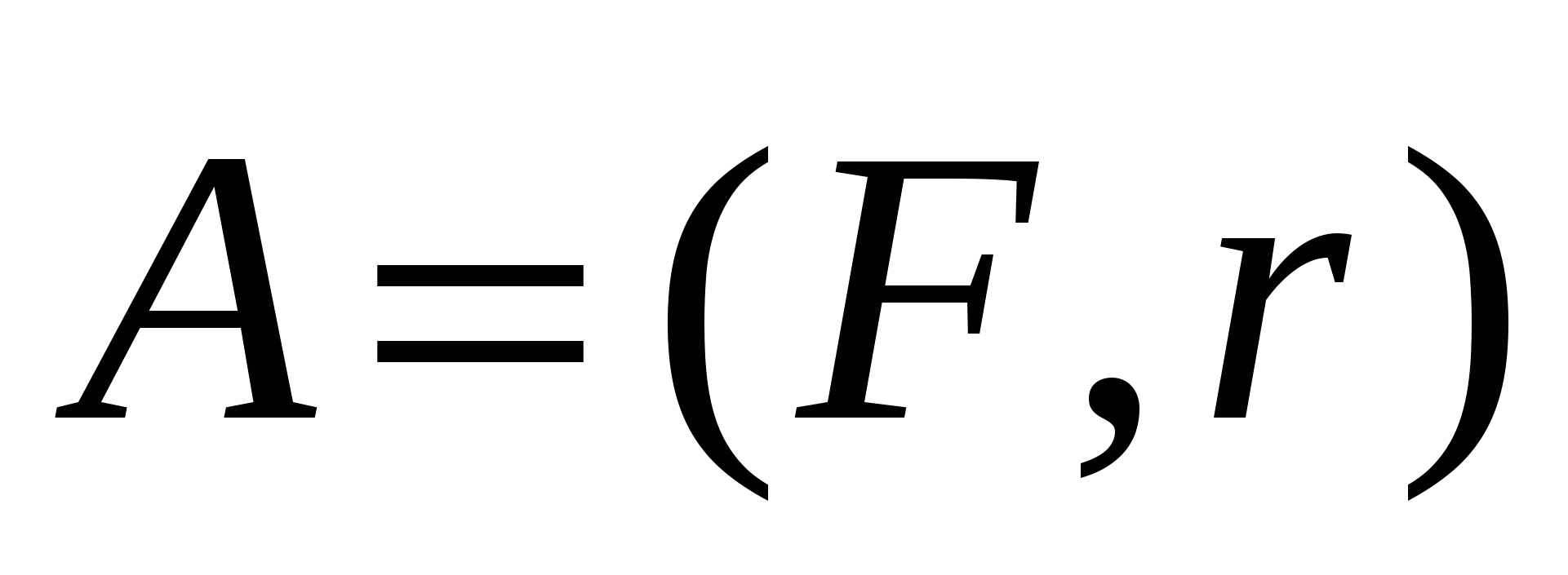 . .
Будем полагать компоненты вектора силы 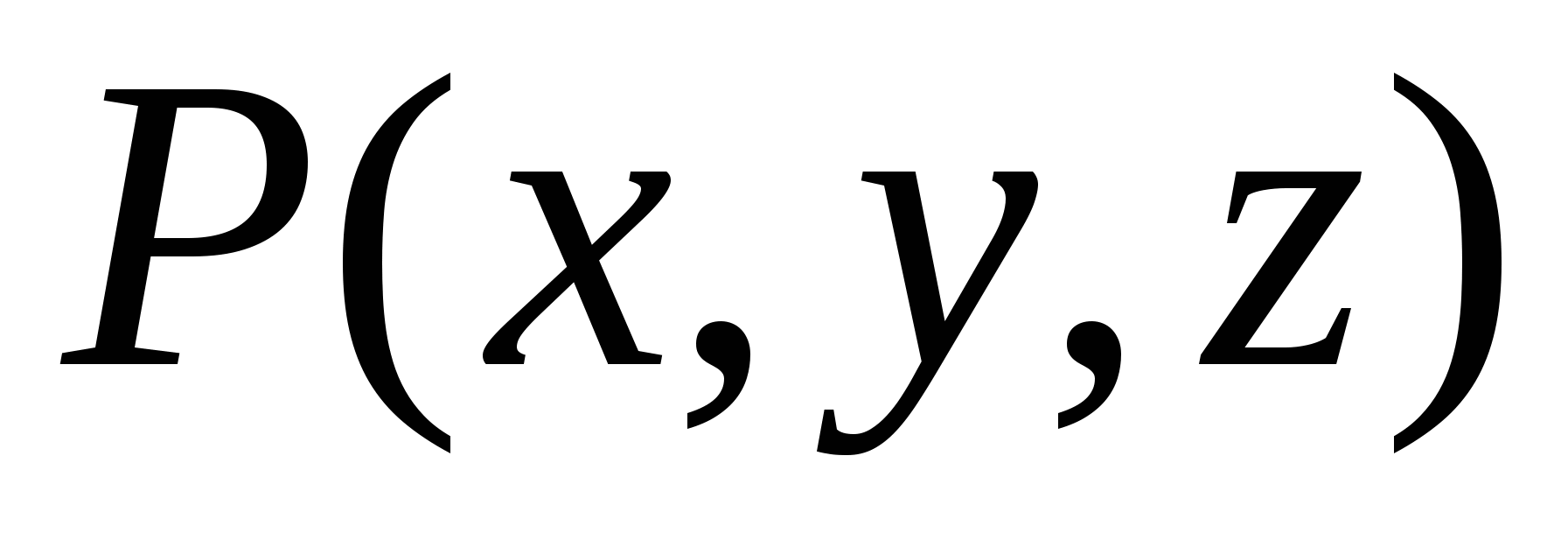 , , 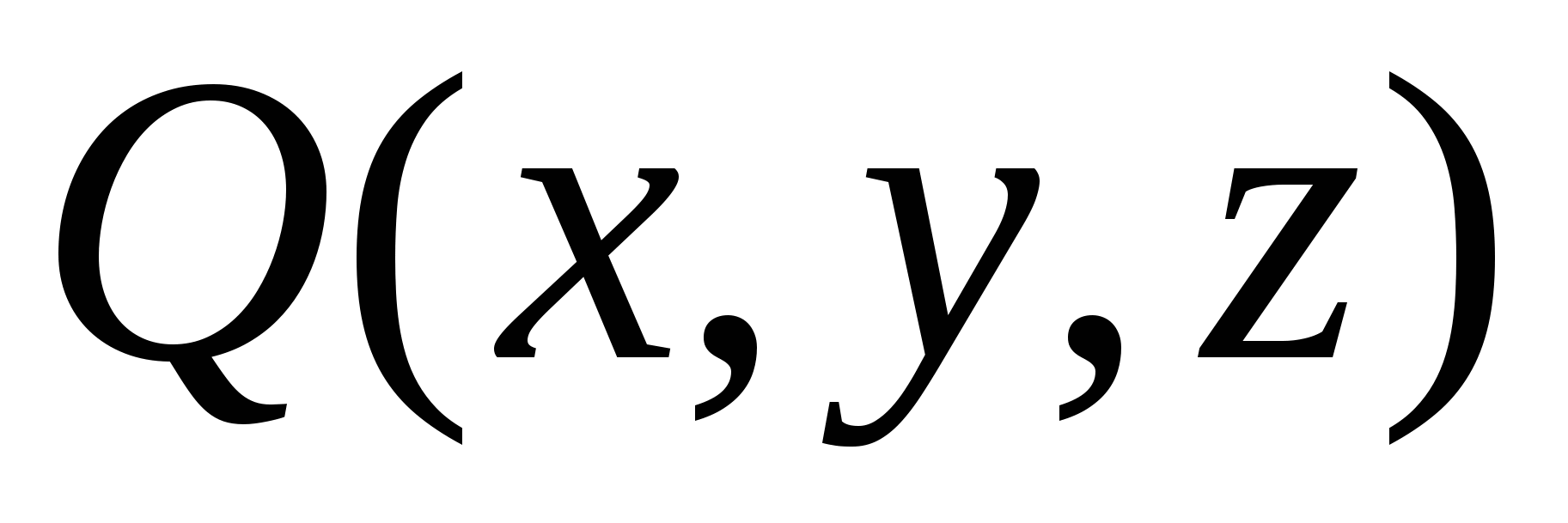 , , 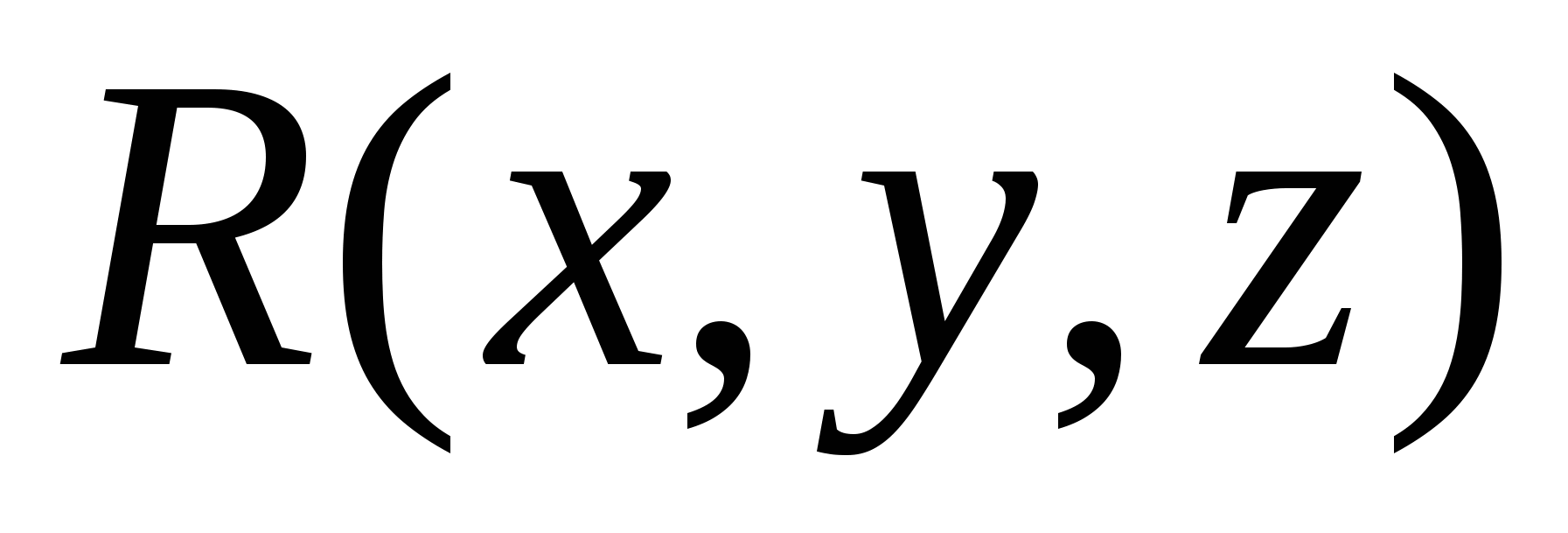 непрерывными на C функциями. Будем считать кривую C гладкой, то есть такой, что в каждой точке кривой существует касательная к кривой в этой точке, а при разбиении кривой точками на дуговые фрагменты и при измельчении такого разбиения хорда, соединяющая концы дугового фрагмента, становится сколь угодно близкой к соответствующему дуговому фрагменту. непрерывными на C функциями. Будем считать кривую C гладкой, то есть такой, что в каждой точке кривой существует касательная к кривой в этой точке, а при разбиении кривой точками на дуговые фрагменты и при измельчении такого разбиения хорда, соединяющая концы дугового фрагмента, становится сколь угодно близкой к соответствующему дуговому фрагменту.
Для вычисления работы силы вдоль кривой разобьем кривую C на n фрагментов точками с координатами 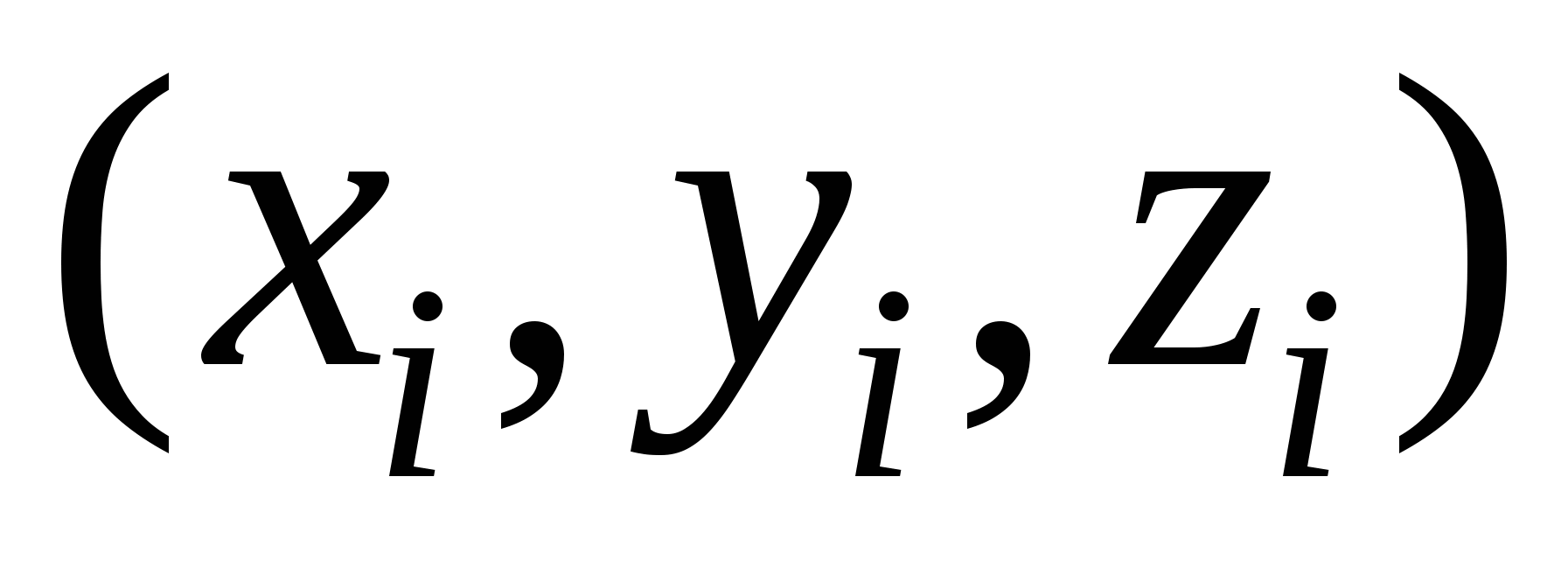 так, что при движении в заданном направлении по кривой параметр i растет. Выберем на i-м дуговом фрагменте точку с координатами так, что при движении в заданном направлении по кривой параметр i растет. Выберем на i-м дуговом фрагменте точку с координатами 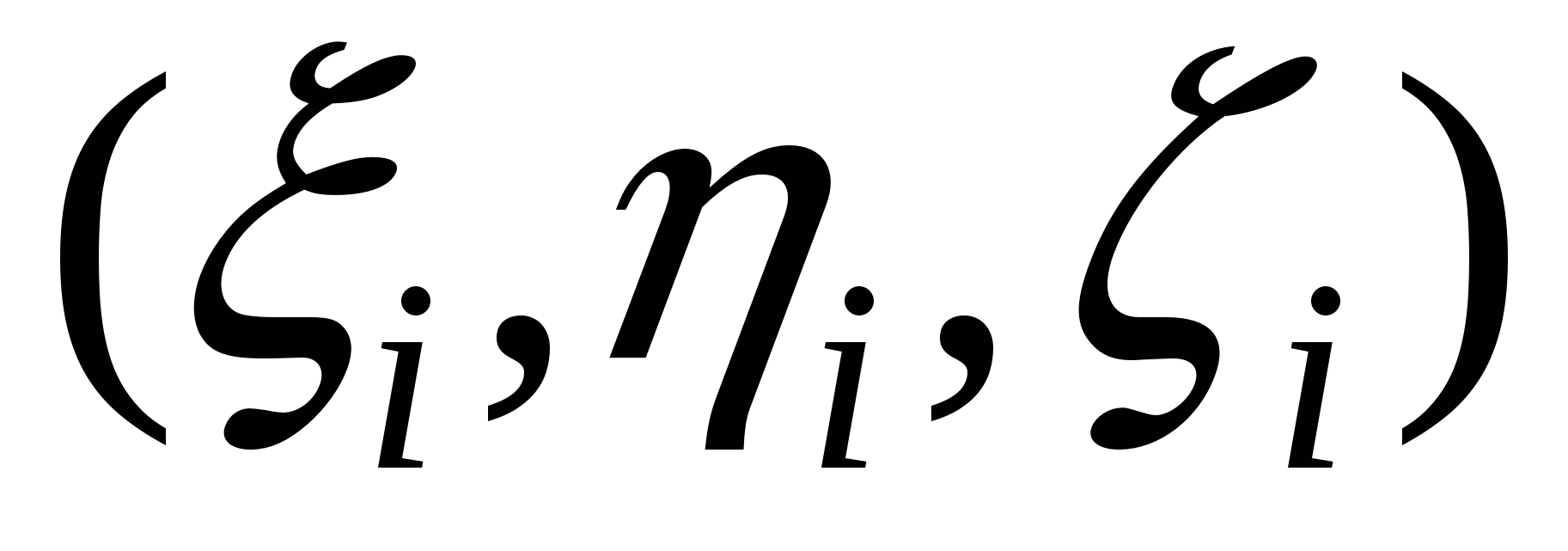 . При измельчении разбиения кривой вектор силы на i-м дуговом фрагменте мало отличается от вектора . При измельчении разбиения кривой вектор силы на i-м дуговом фрагменте мало отличается от вектора 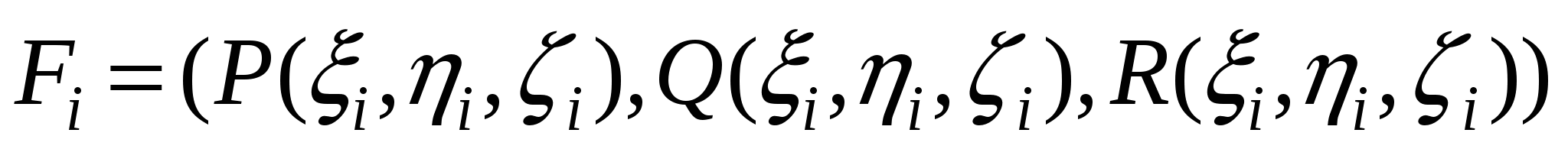 вследствие непрерывности компонент вектора силы. В свою очередь, путь вдоль i-го дугового фрагмента от точки с координатами вследствие непрерывности компонент вектора силы. В свою очередь, путь вдоль i-го дугового фрагмента от точки с координатами 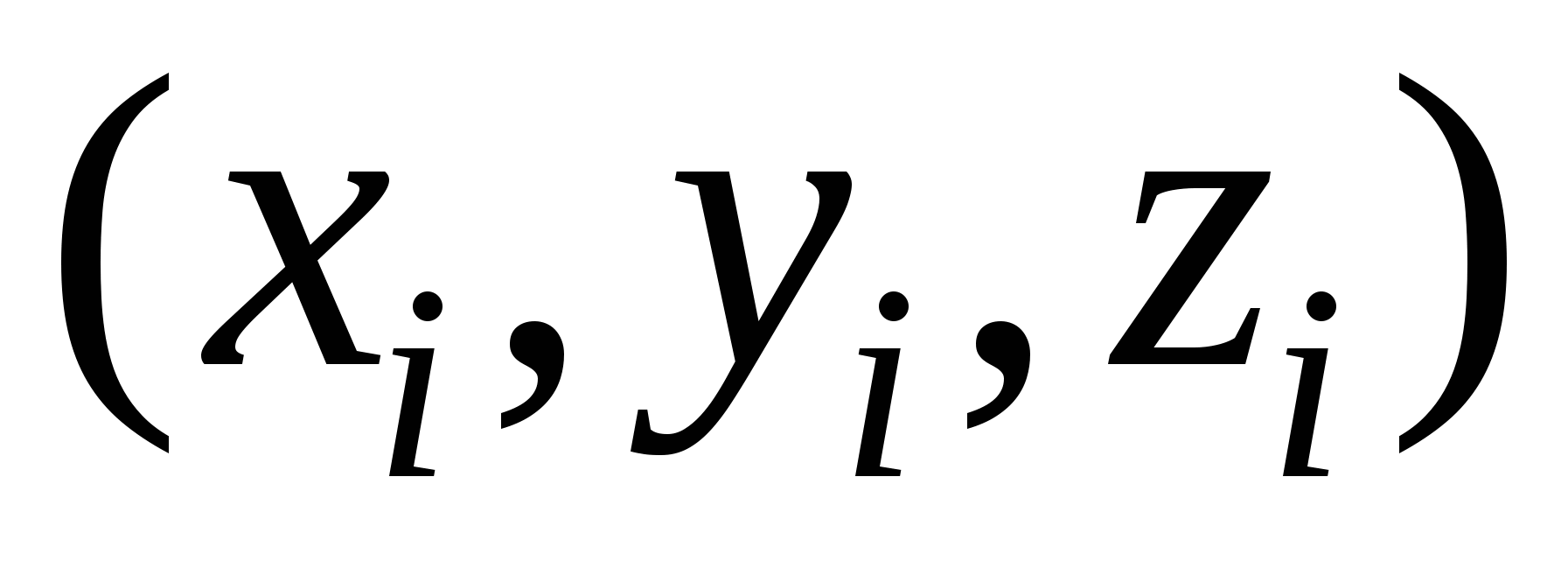 к точке с координатами к точке с координатами 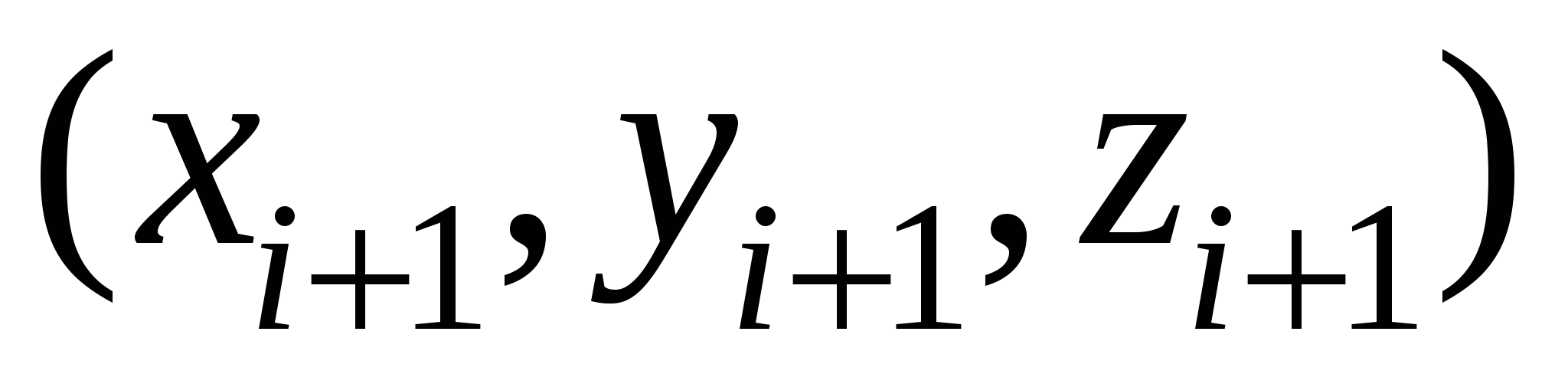 при измельчении разбиения мало отличается от пути вдоль соответствующей хорды. Прямолинейный путь вдоль хорды задается вектором при измельчении разбиения мало отличается от пути вдоль соответствующей хорды. Прямолинейный путь вдоль хорды задается вектором 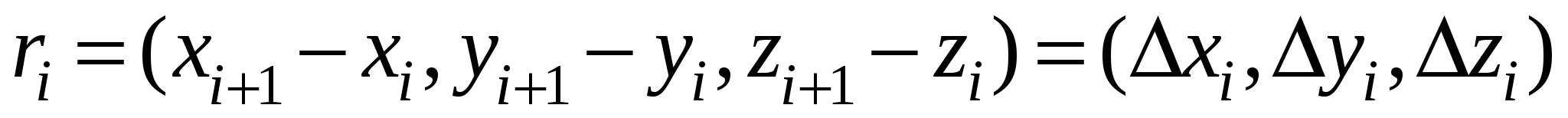 , причем измельчение разбиения равносильно стремлению к нулю компонент вектора , причем измельчение разбиения равносильно стремлению к нулю компонент вектора 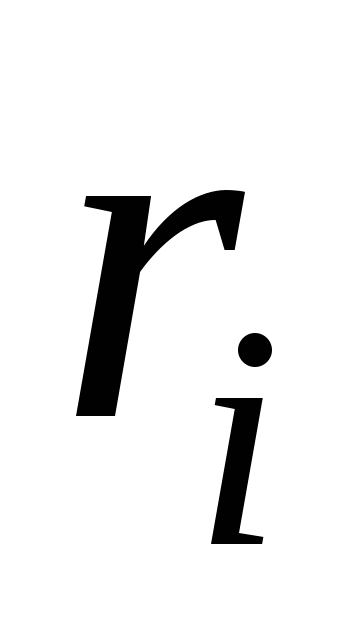 . Таким образом, работа силы вдоль i-го дугового фрагмента близка к значению . Таким образом, работа силы вдоль i-го дугового фрагмента близка к значению 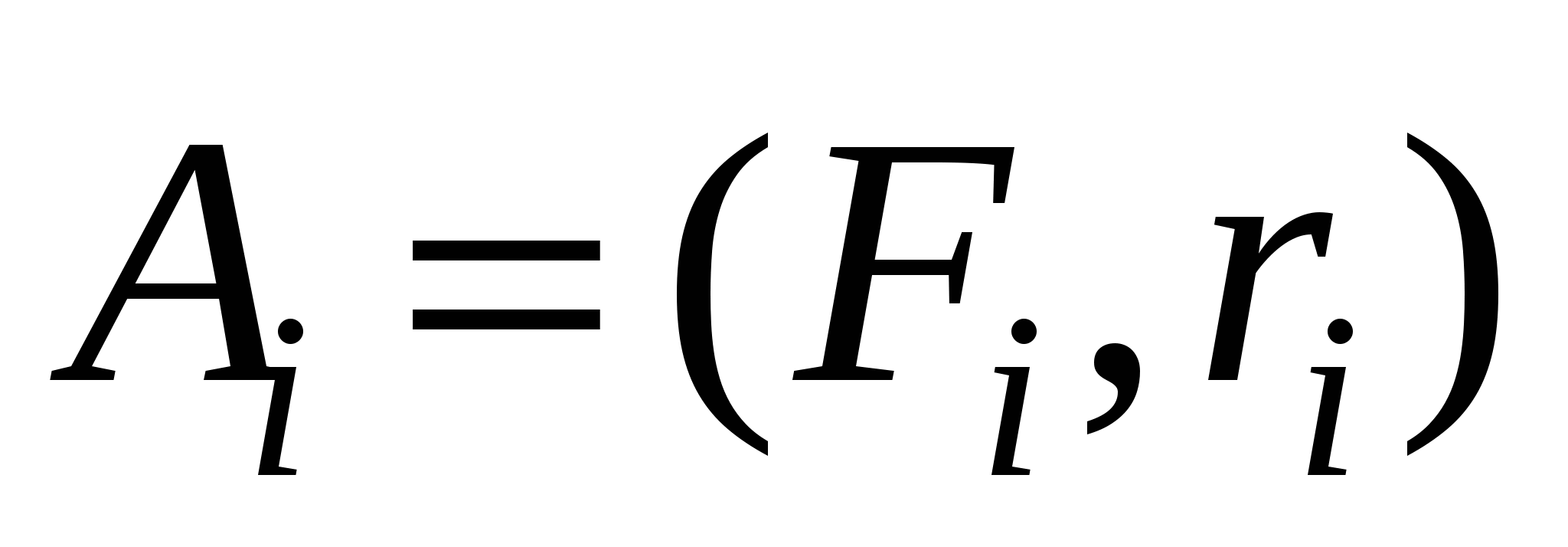 , и это значение тем точнее, чем мельче разбиение кривой C. , и это значение тем точнее, чем мельче разбиение кривой C.
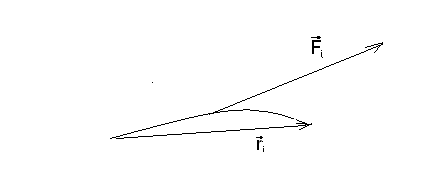
Работу вдоль всей кривой C мы получим, если просуммируем значения работы на всех дуговых фрагментах кривой C, измельчая разбиение и увеличивая одновременно количество дуговых фрагментов:
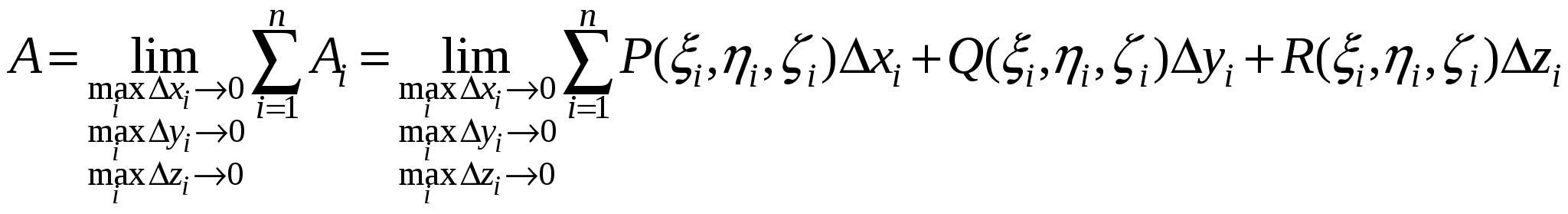 . .
Переходя от предела интегральных сумм к интегралу, имеем
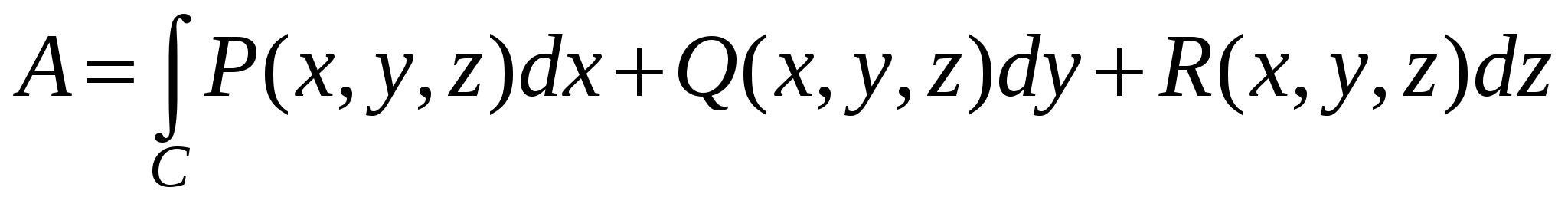 . .
Интеграл в правой части последнего выражения называется криволинейным интегралом второго рода или криволинейным интегралом по координатам. Этот интеграл вычисляют только вдоль ориентированных кривых – то есть, кривых, на которых задано направление. Заметим, что, если мы сменим направление движения вдоль кривой C на противоположное, а значит, заменим при вычислении  вектор вектор 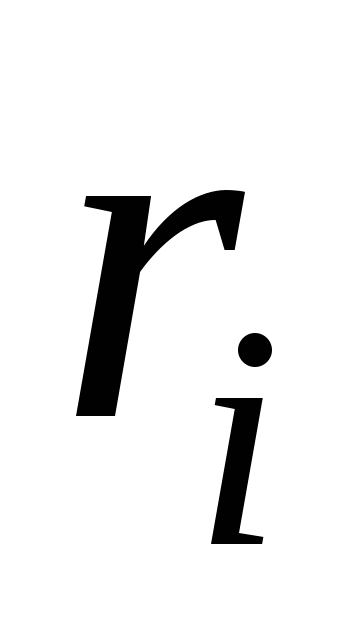 на вектор на вектор 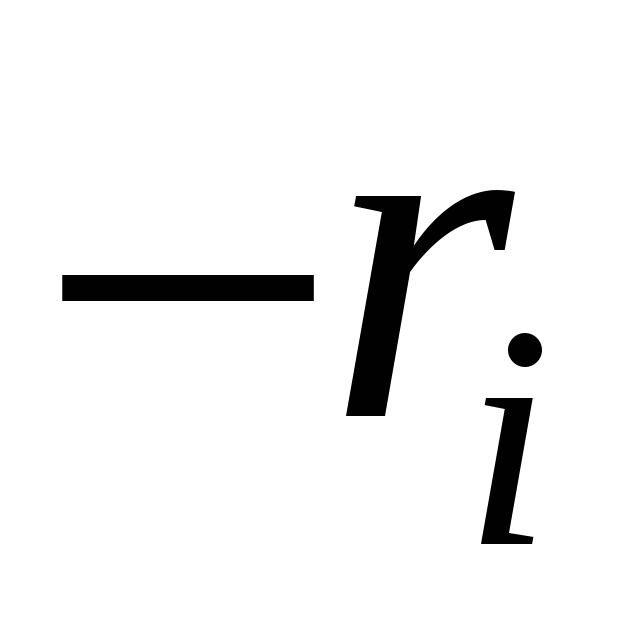 , то получим замену знака , то получим замену знака  на противоположный знак. Поэтому при задании криволинейного интеграла второго рода обязательно задают направление движения по кривой интегрирования. на противоположный знак. Поэтому при задании криволинейного интеграла второго рода обязательно задают направление движения по кривой интегрирования.
Как и интеграл по отрезку, криволинейный интеграл по непрерывной кривой, состоящей из нескольких фрагментов, равен сумме криволинейных интегралов по этим фрагментам. Поэтому можно рассматривать криволинейный интеграл и по кусочно-гладкой кривой, то есть, непрерывной кривой, состоящей из конечного числа гладких фрагментов.
В случае, когда кривая C замкнута, символ интеграла обычно несколько изменяют, добавляя пересекающий его кружок: 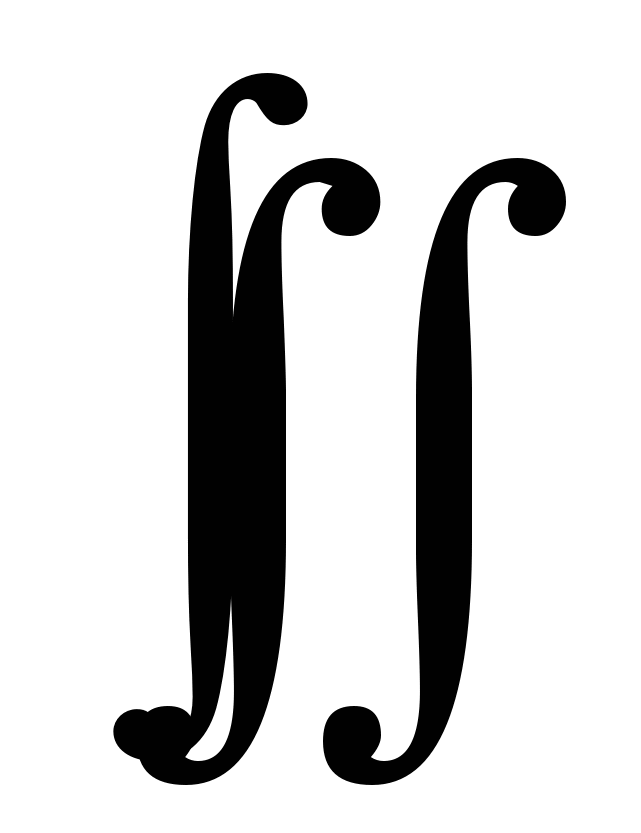 . .
Способ вычисления криволинейного интеграла второго рода.
Пусть требуется вычислить 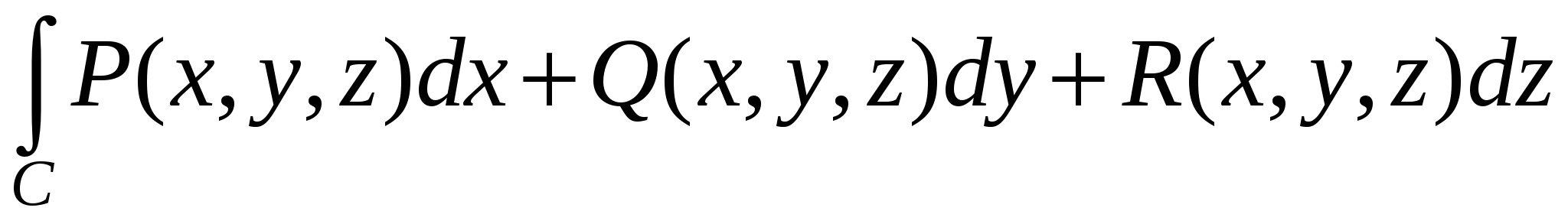 . .
Кривая C задана параметрически: 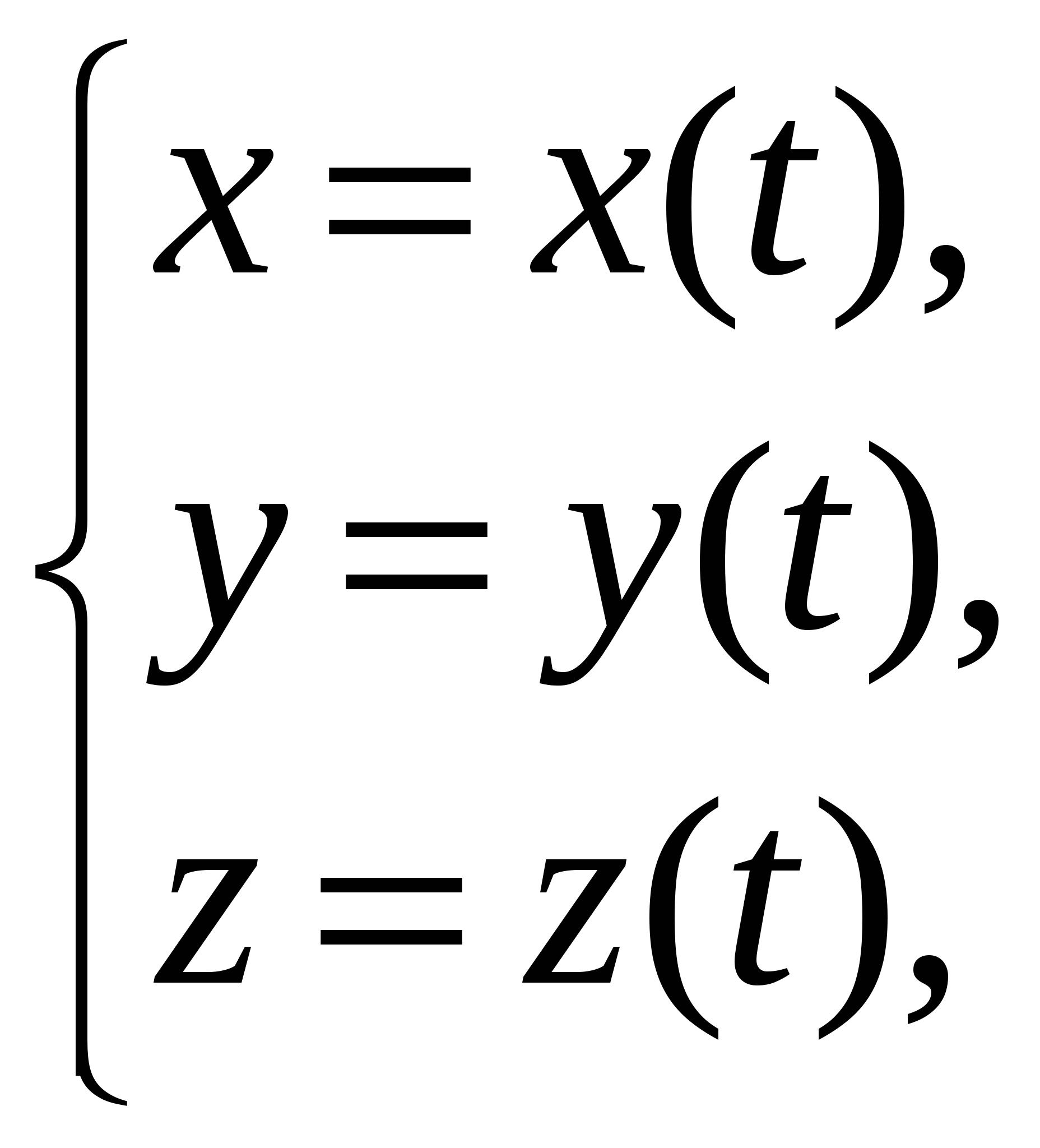 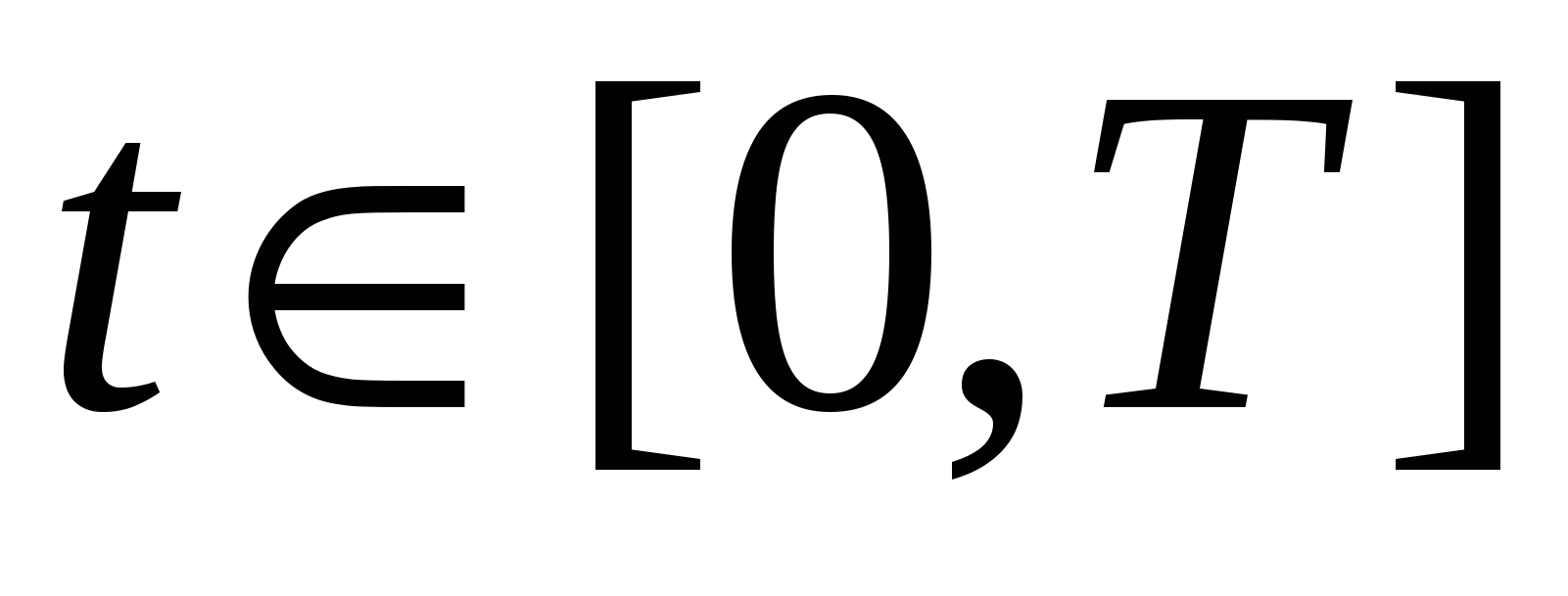 , где функции , где функции 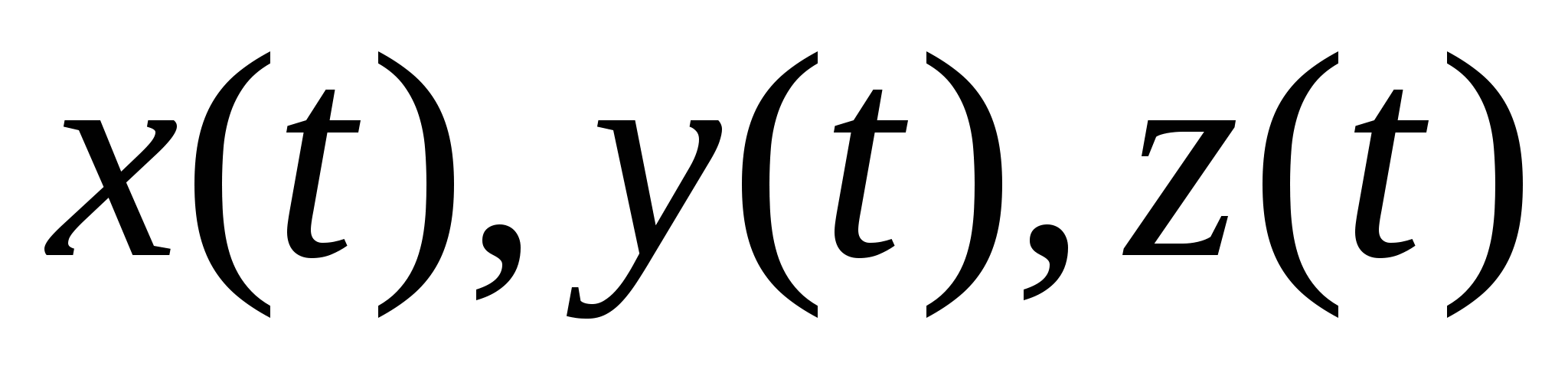 имеют непрерывные на отрезке имеют непрерывные на отрезке 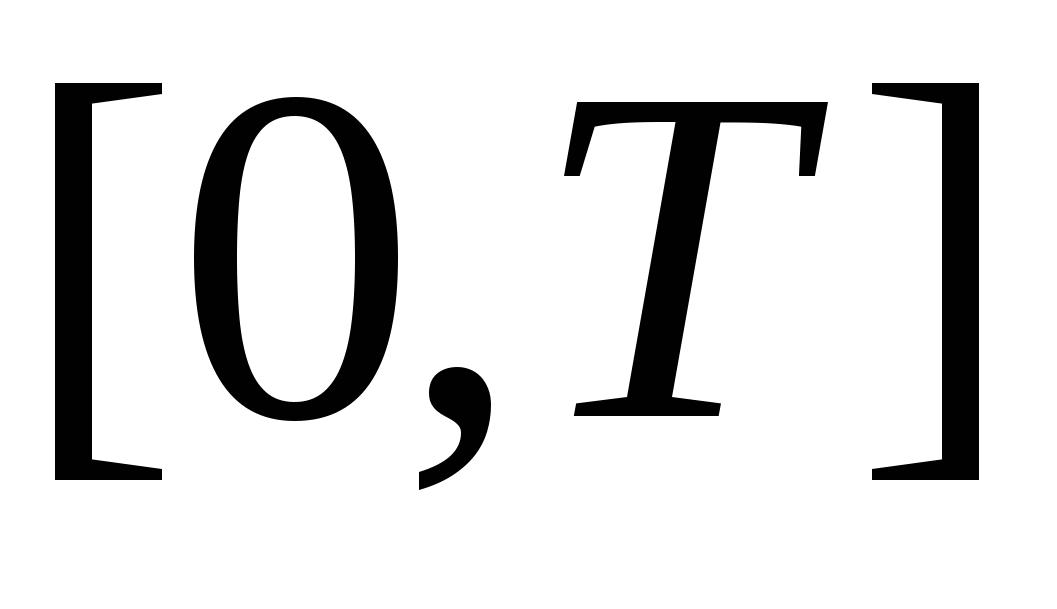 производные. Точки разбиения кривой C на фрагменты задают разбиение отрезка значений параметра производные. Точки разбиения кривой C на фрагменты задают разбиение отрезка значений параметра 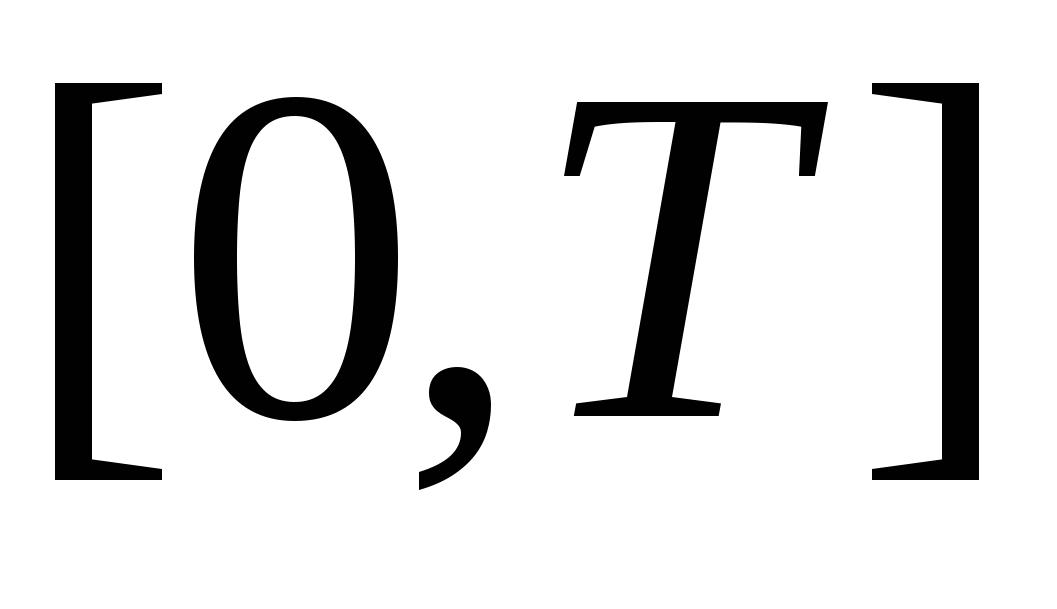 на отрезки на отрезки 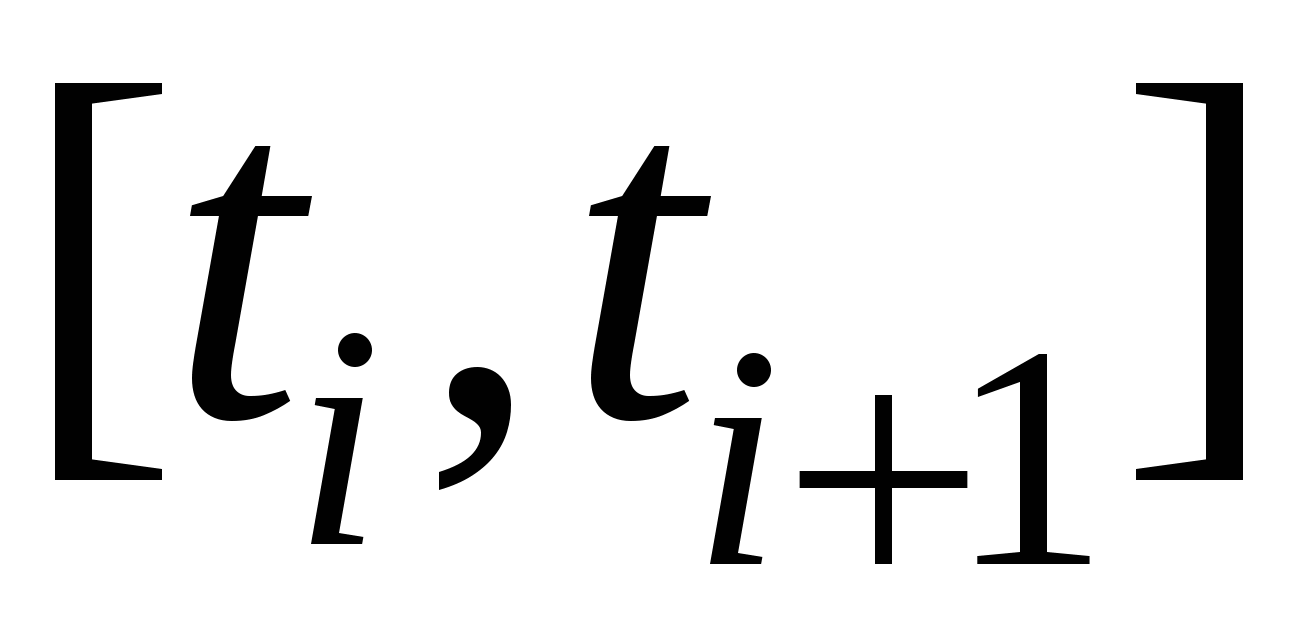 , , 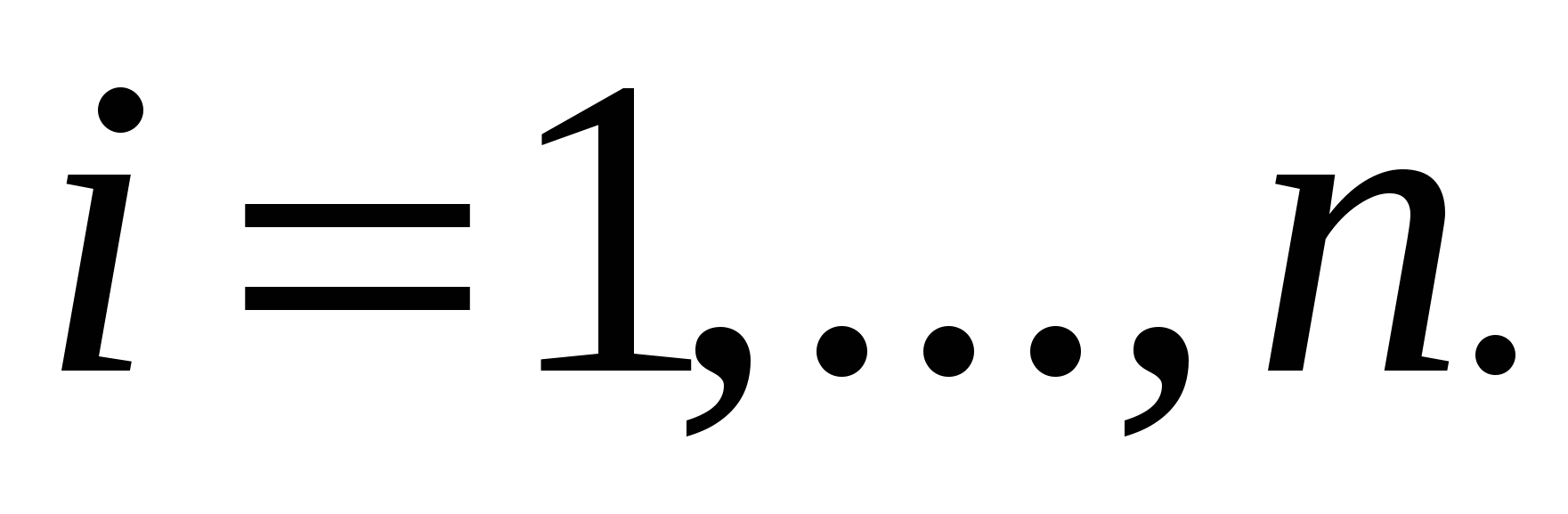 Найдем на i-м отрезке точку Найдем на i-м отрезке точку 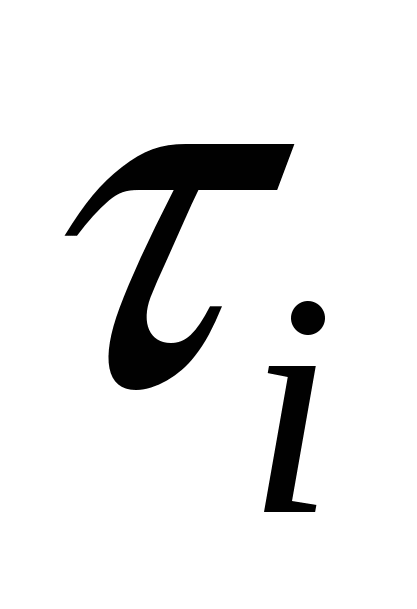 такую, что такую, что 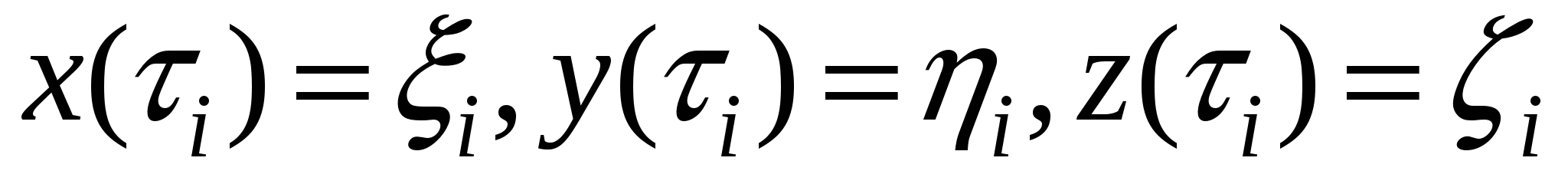 , где , где 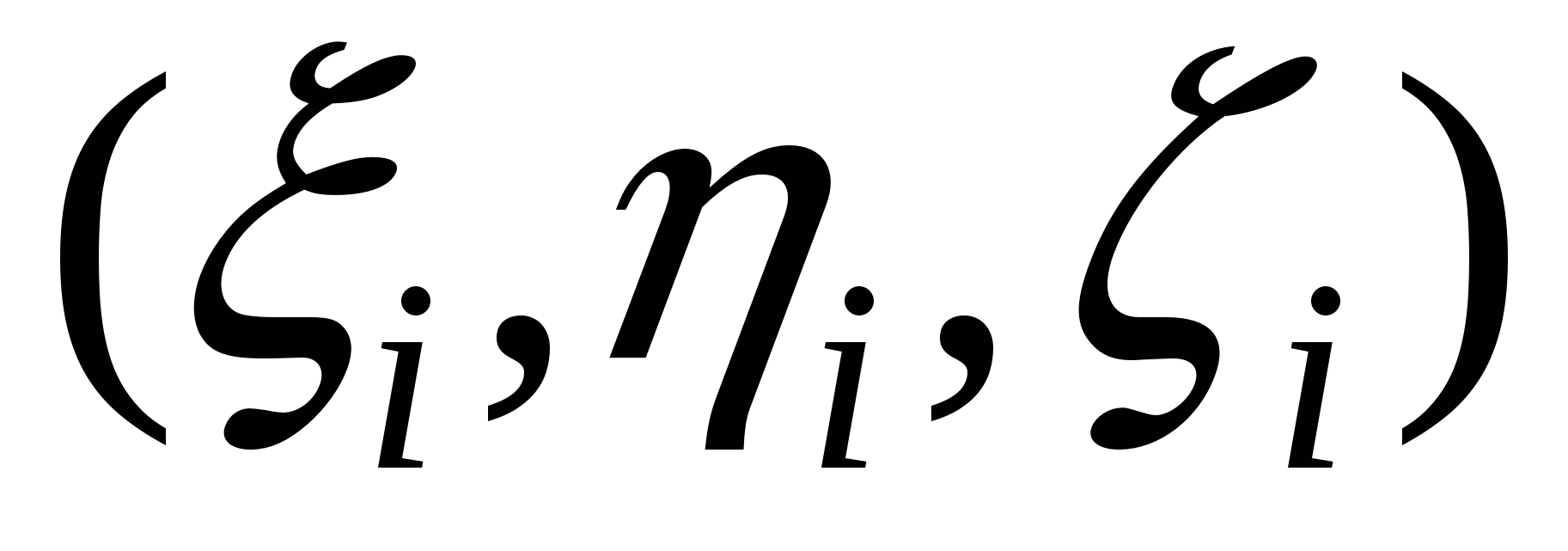 – координаты выбранной точки на i-м фрагменте кривой. Заменим в представлении интегральной суммы – координаты выбранной точки на i-м фрагменте кривой. Заменим в представлении интегральной суммы
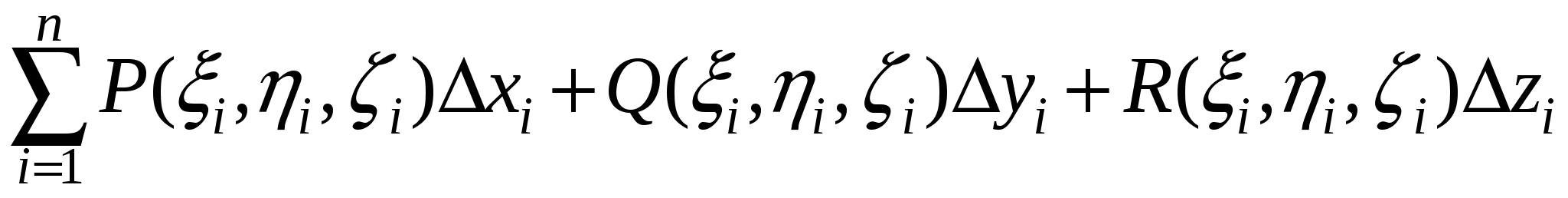
приращение 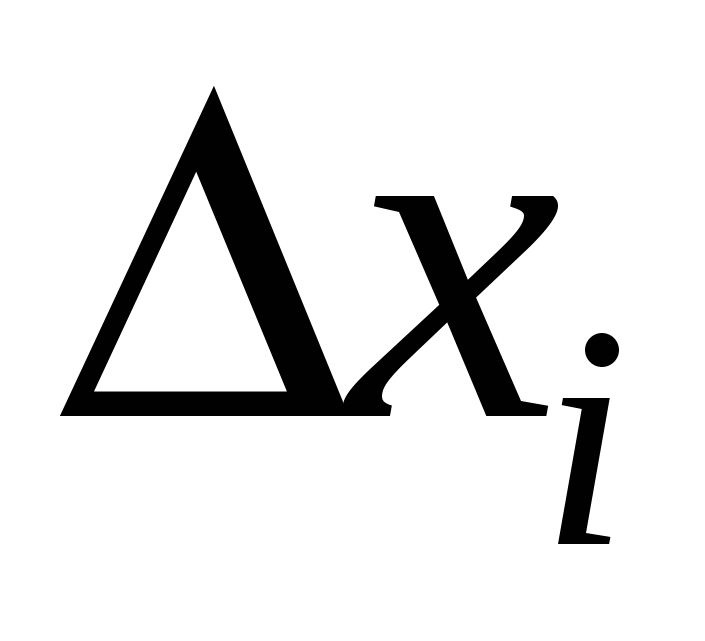 на на 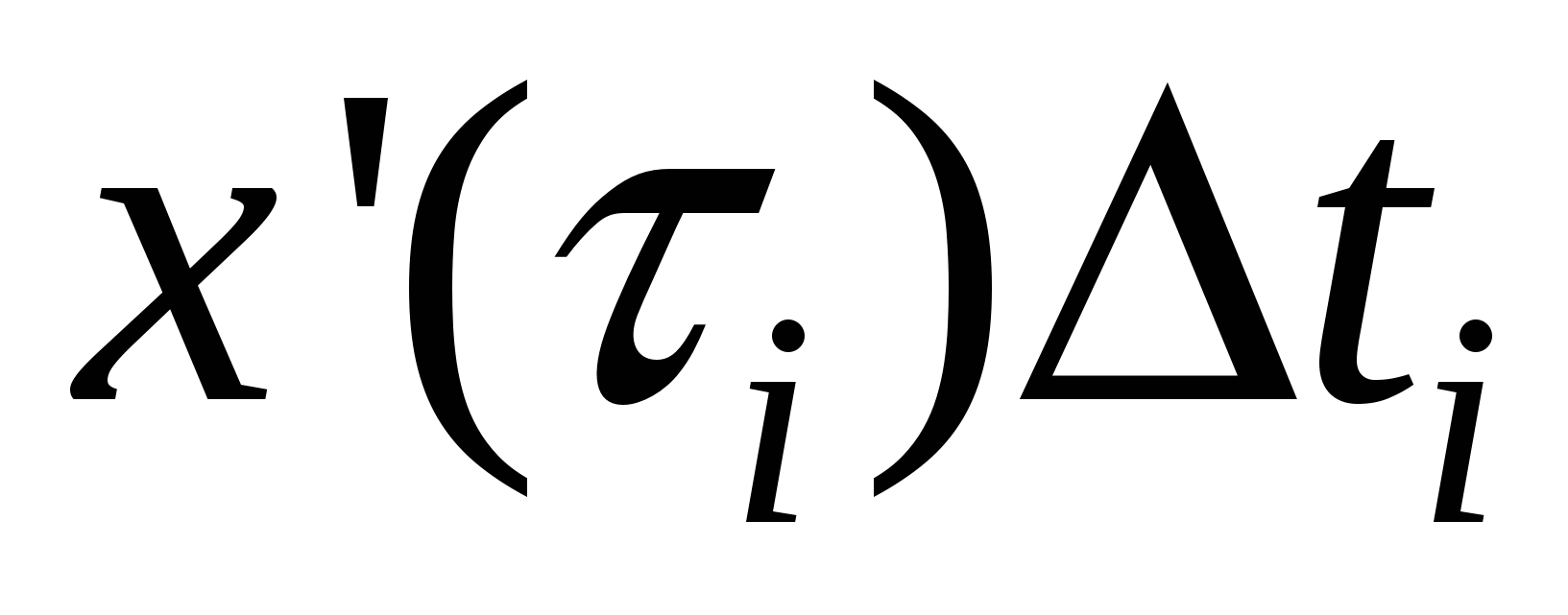 , приращение , приращение 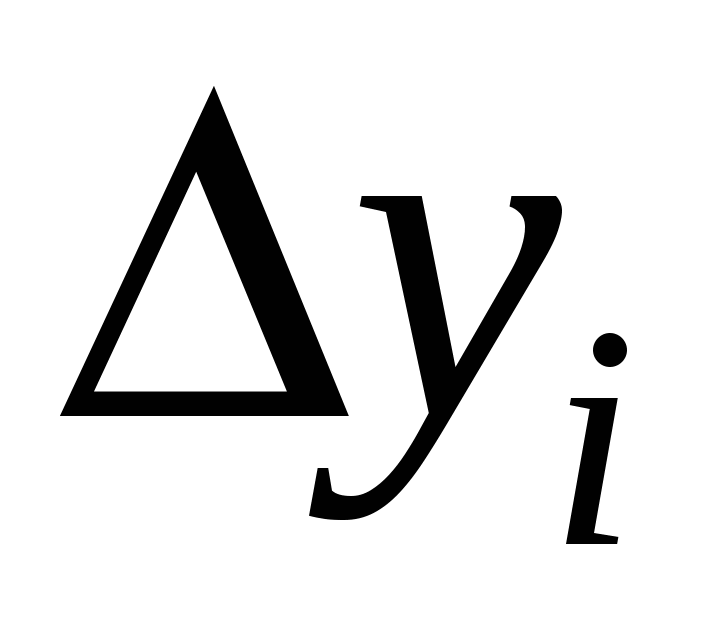 на на 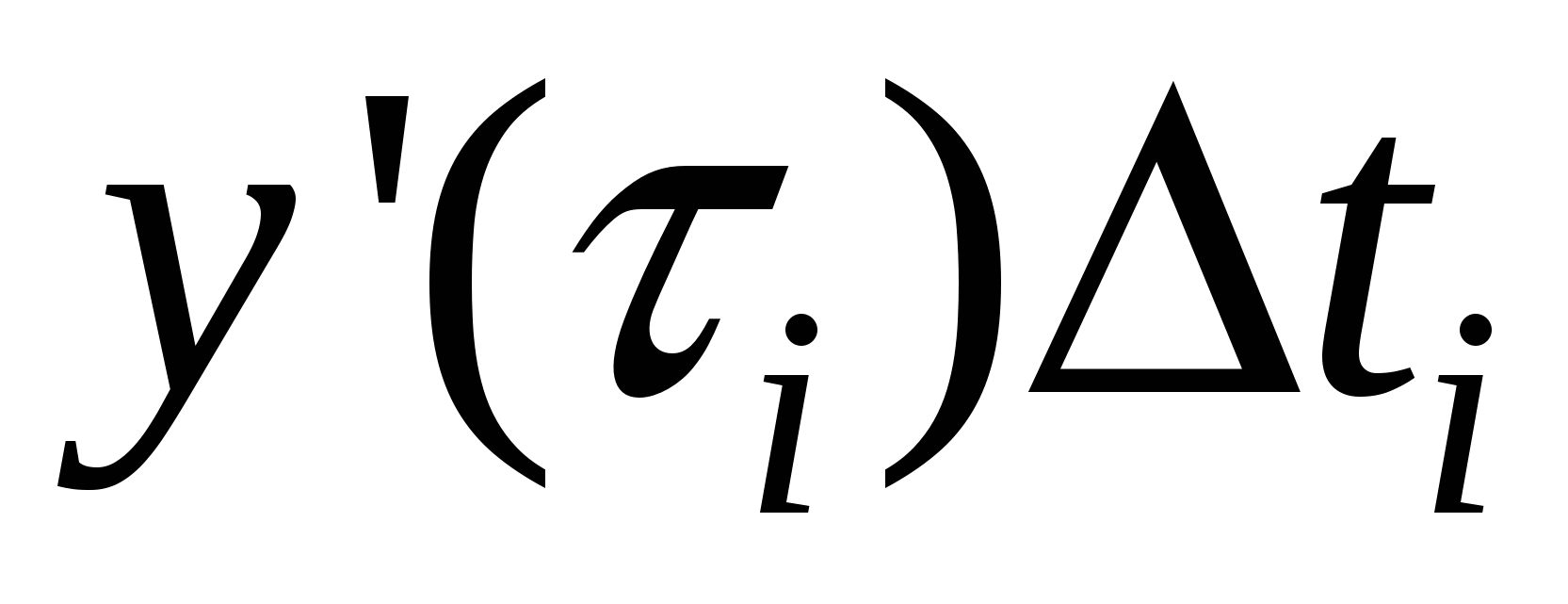 , приращение , приращение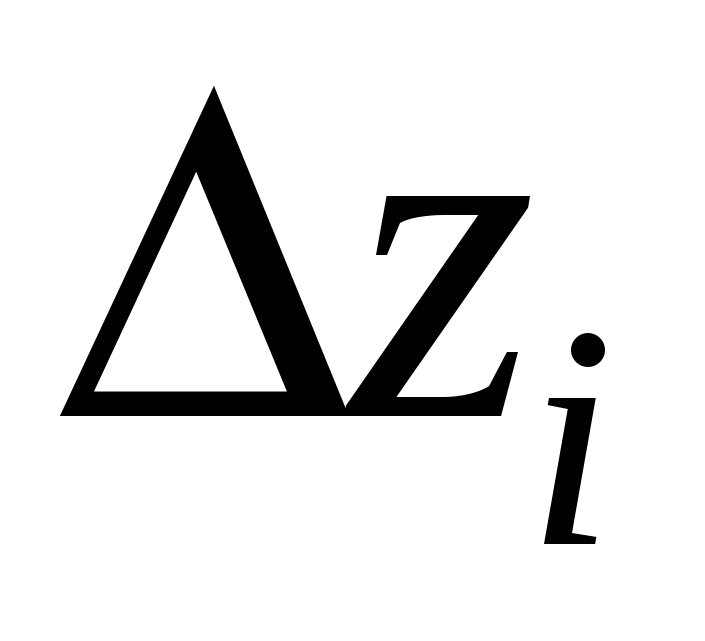 на на 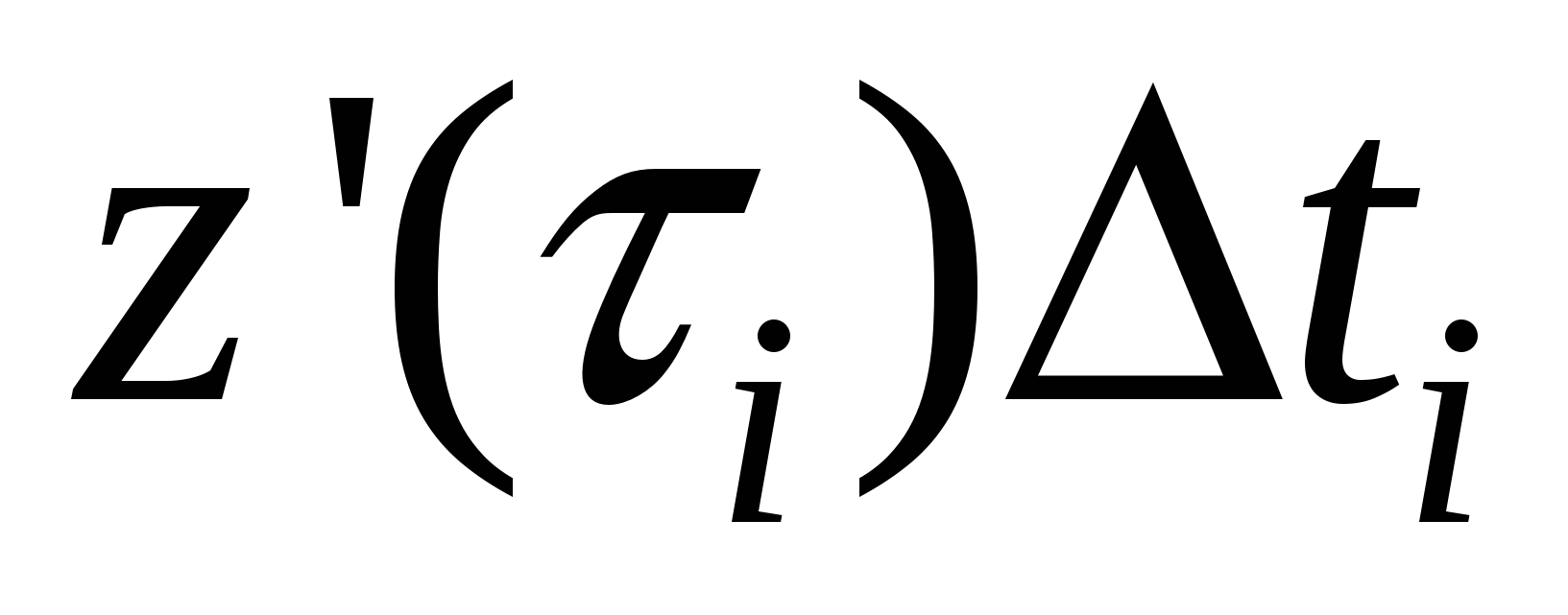 , где , где 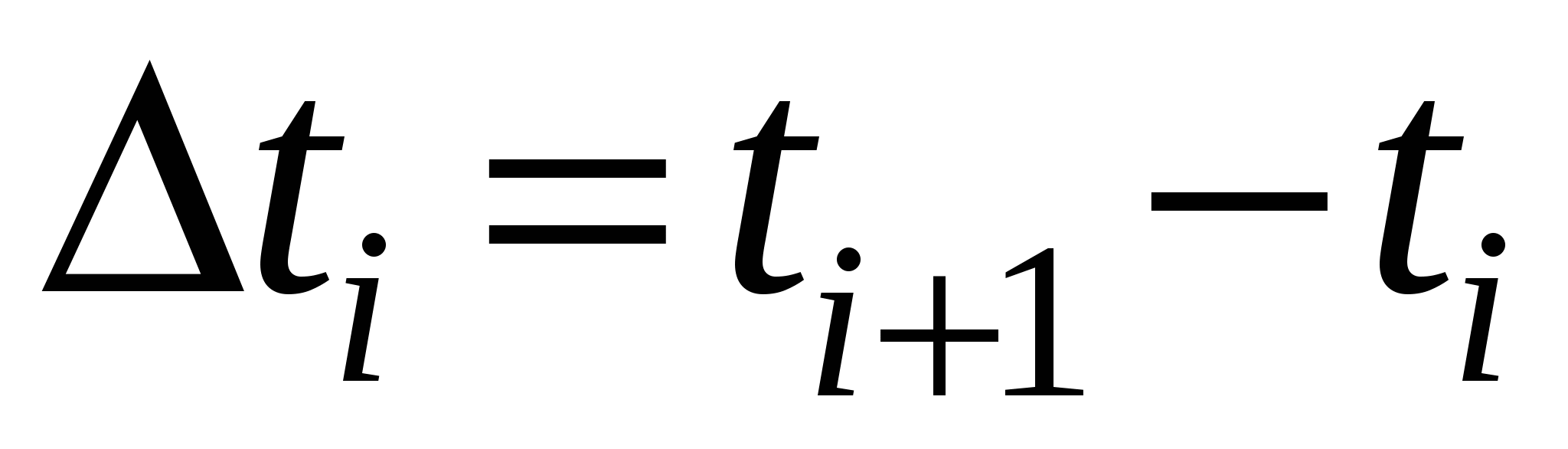 . Это возможно в силу непрерывности функций . Это возможно в силу непрерывности функций 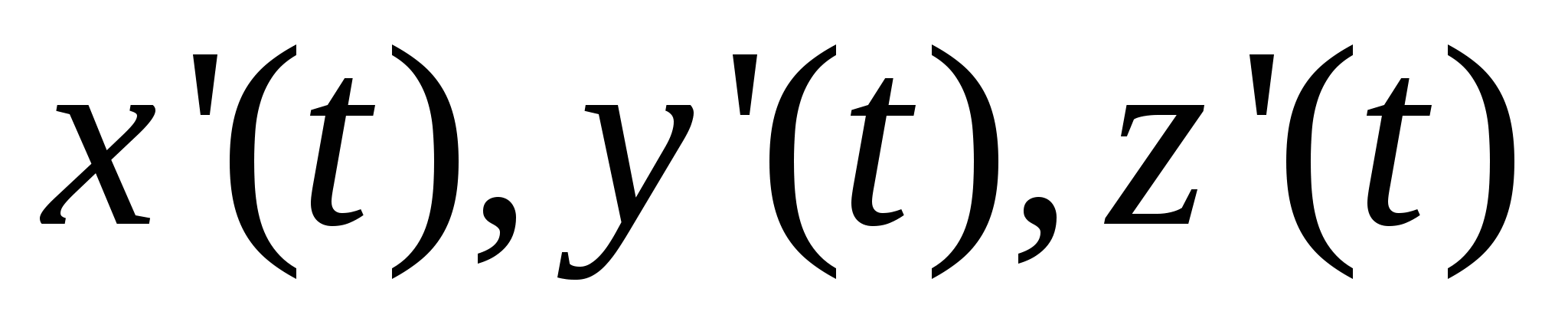 и стремления и стремления 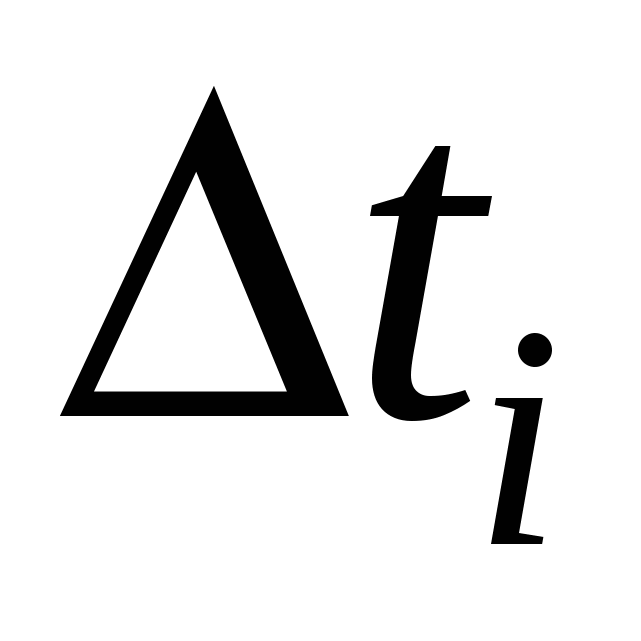 к нулю при измельчении разбиения. Мы имеем интегральную сумму для отрезка к нулю при измельчении разбиения. Мы имеем интегральную сумму для отрезка 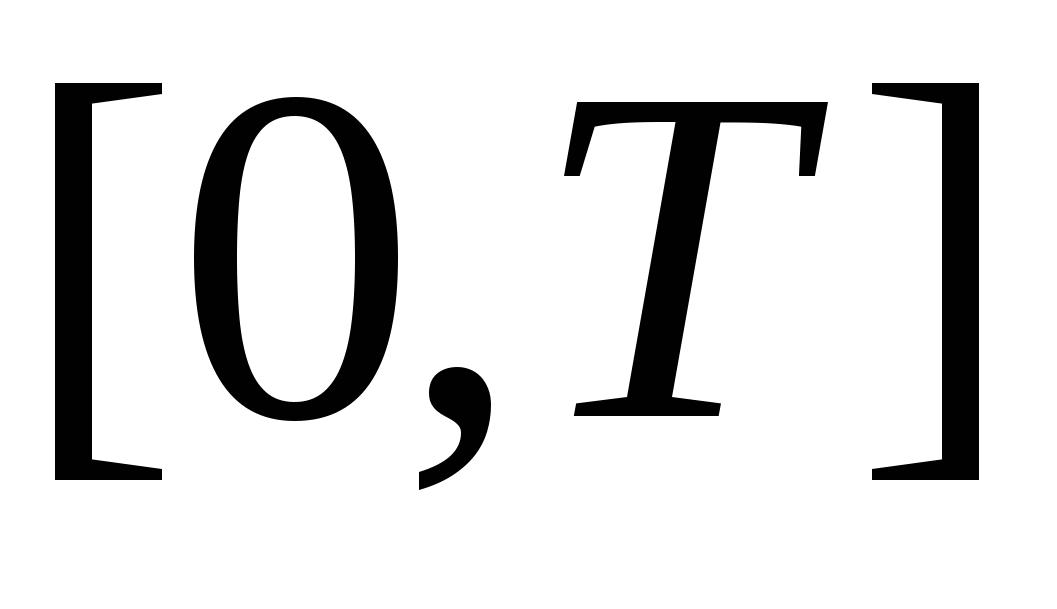 : : 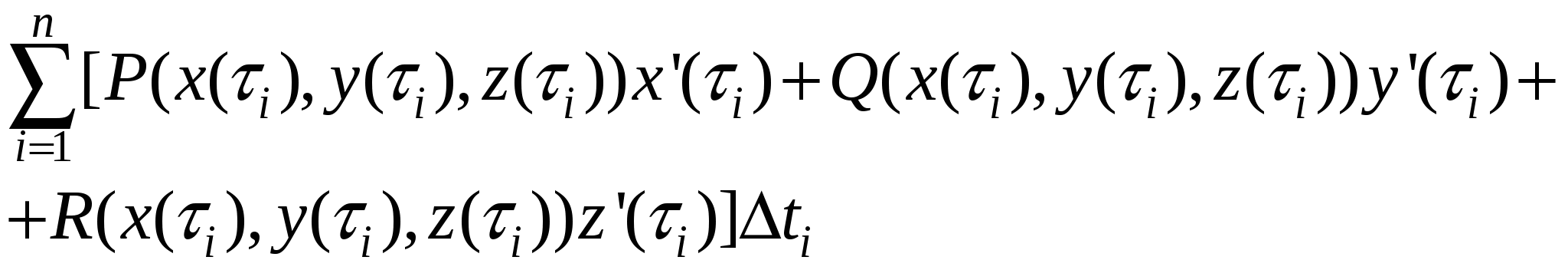 . .
Переходя к пределу при 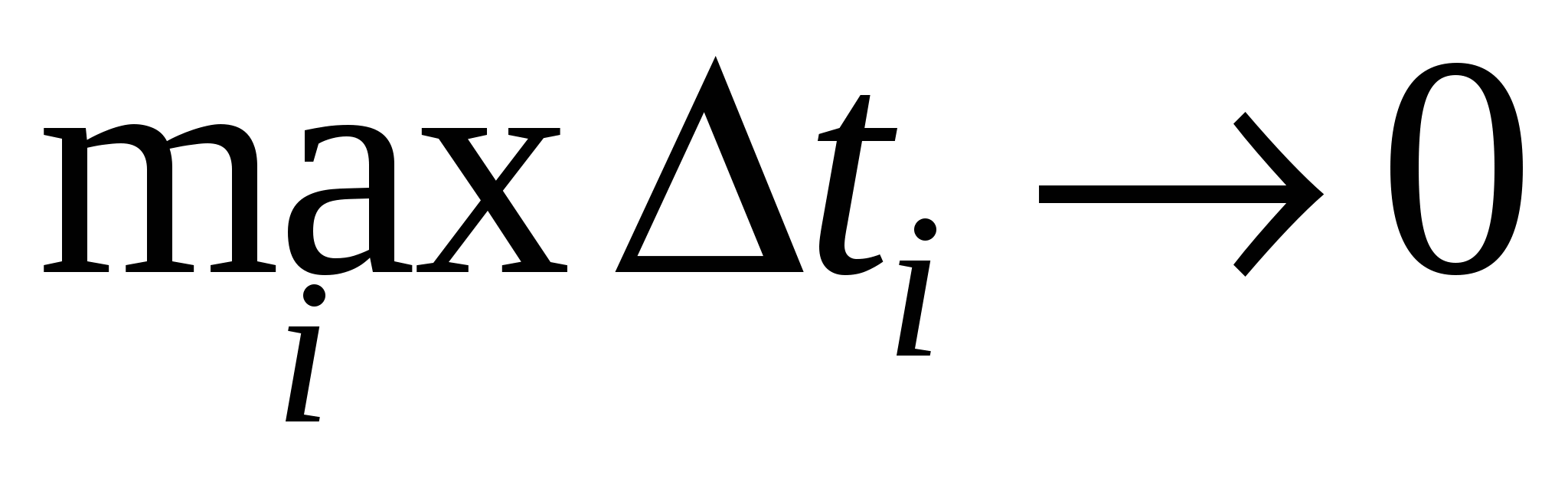 , получим , получим
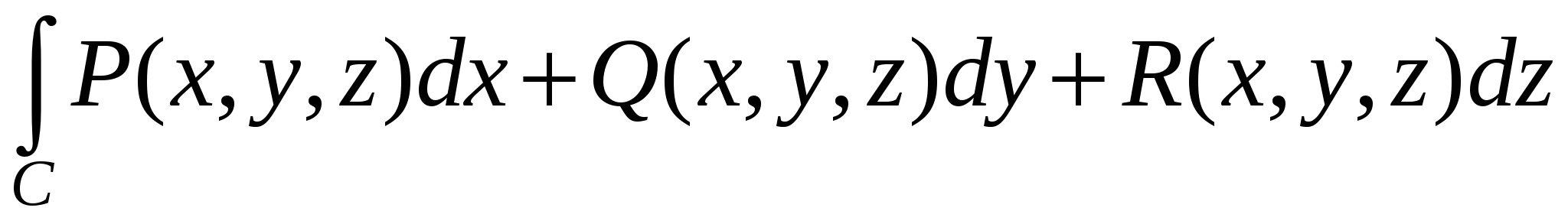 = = 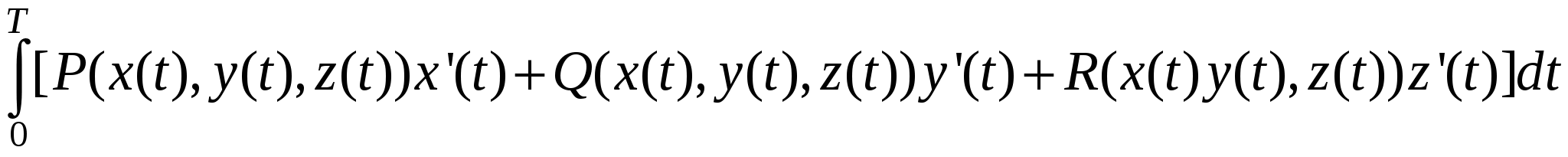 . .
П р и м е р ы.
Вычислить 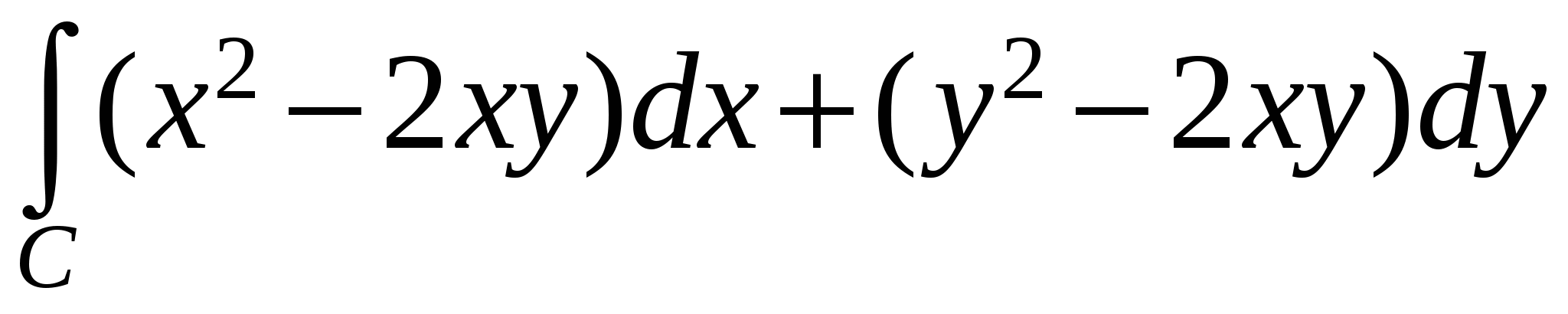 , где C – парабола , где C – парабола 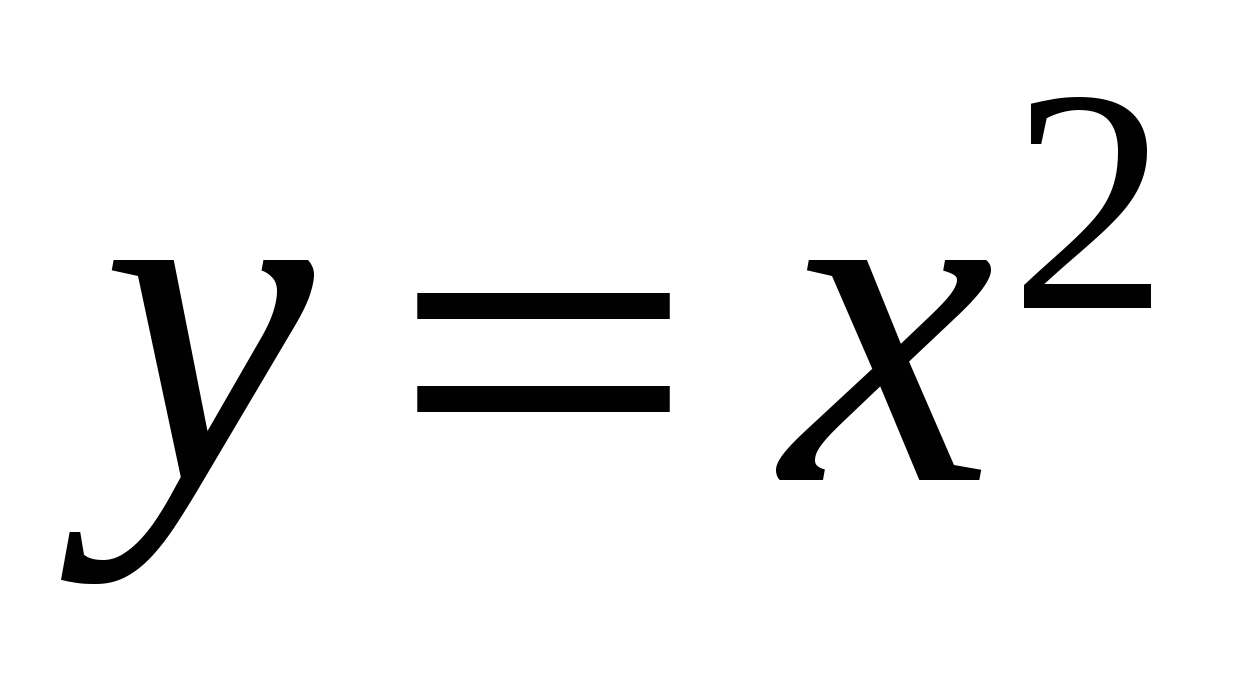 , , 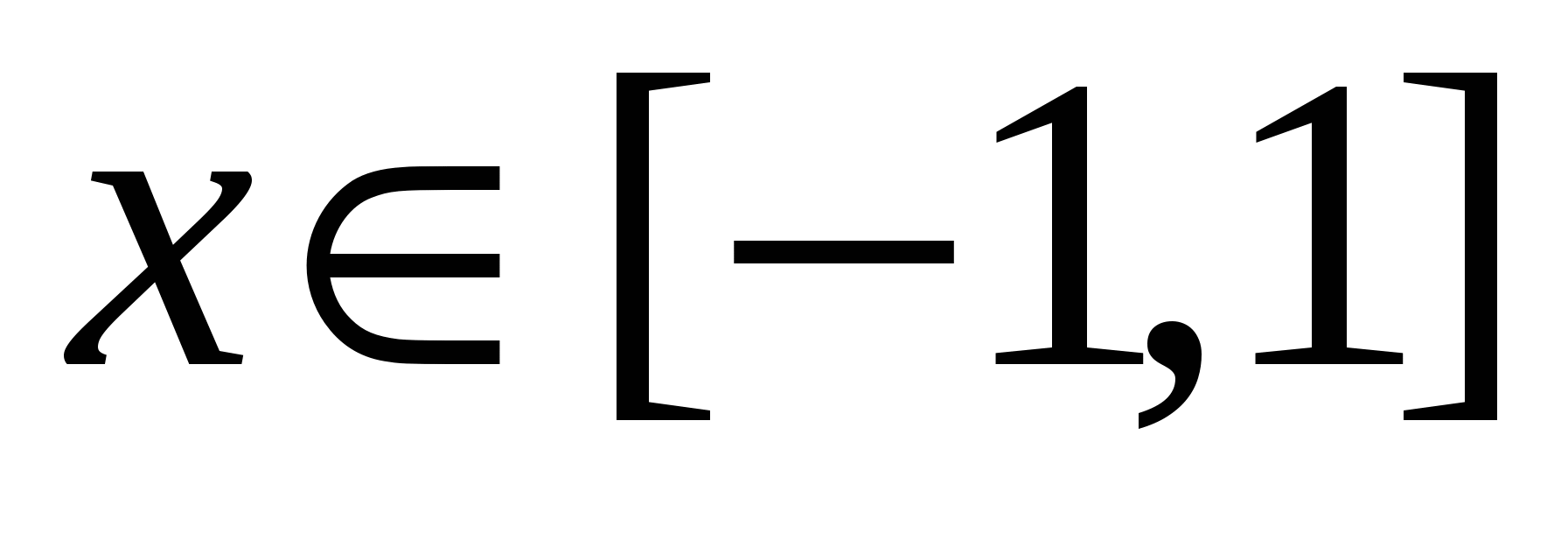 , в плоскости XY, пробегаемая в направлении возрастания , в плоскости XY, пробегаемая в направлении возрастания 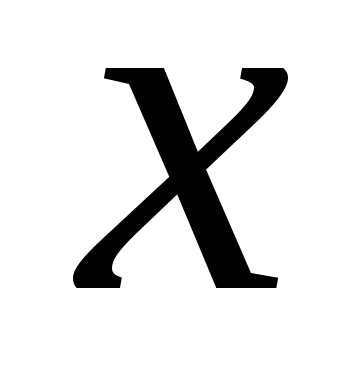 . .
Р е ш е н и е. В качестве параметра для уравнения кривой C можно выбрать переменную x. То есть, параметрическое уравнение кривой имеет вид 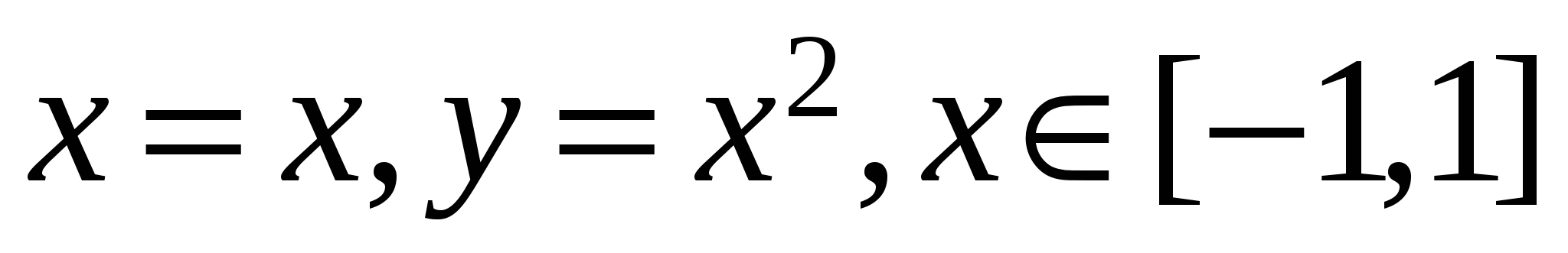 . Поскольку кривая находится в плоскости XY, имеем . Поскольку кривая находится в плоскости XY, имеем 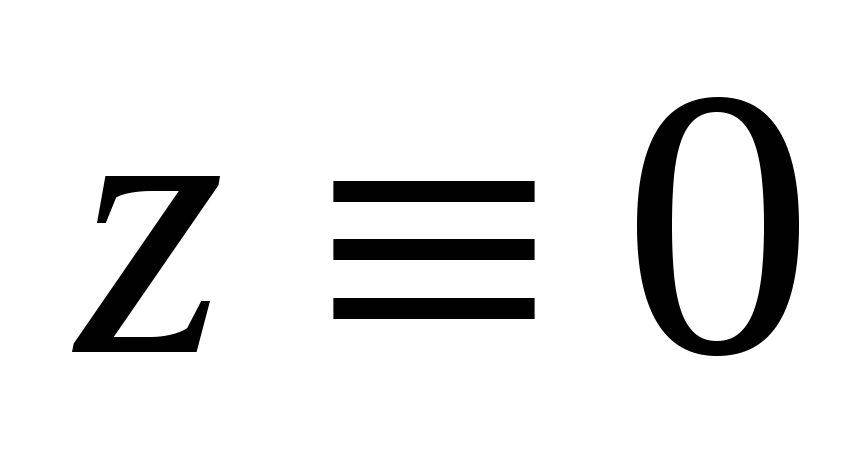 . Поэтому в соответствии с формулой для вычисления криволинейного интеграла второго рода . Поэтому в соответствии с формулой для вычисления криволинейного интеграла второго рода
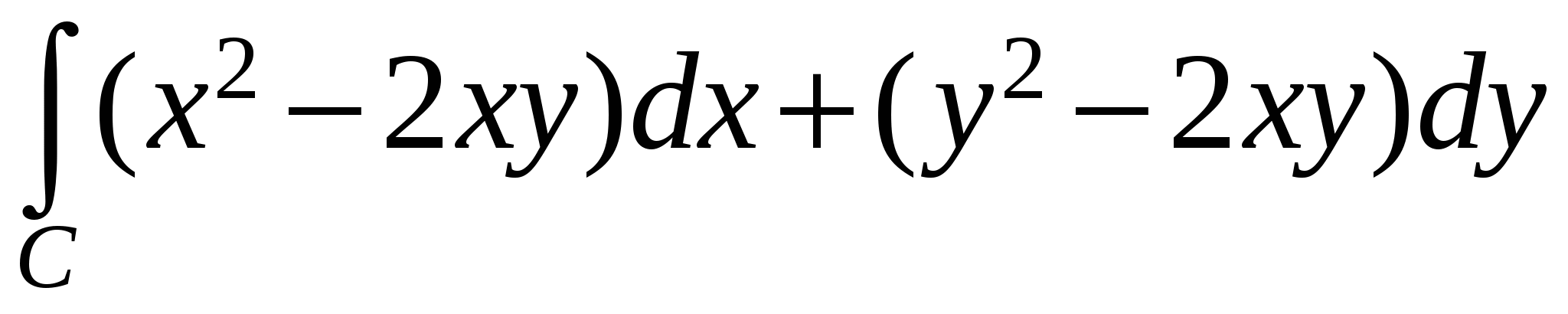 = =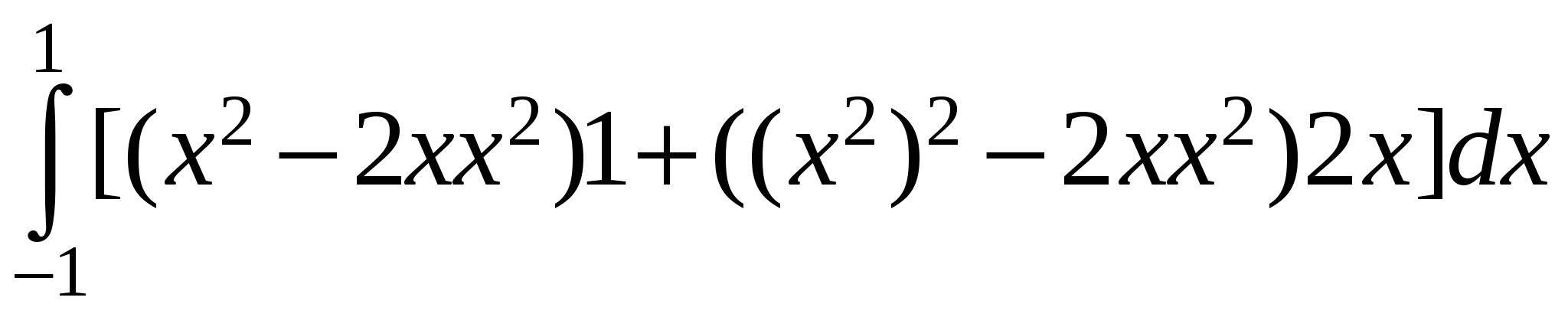 = = = =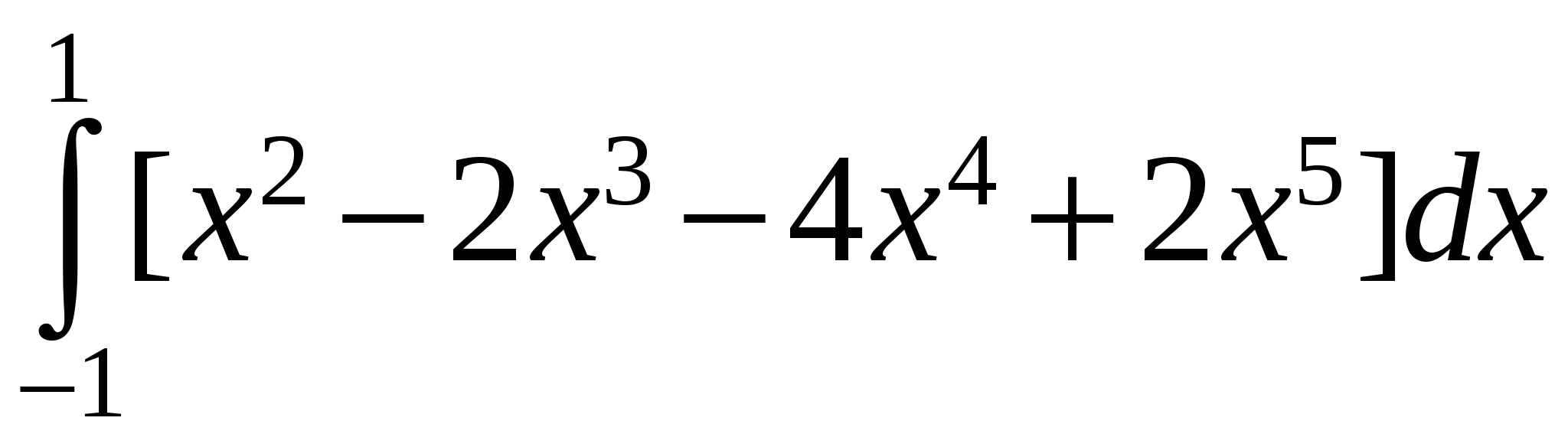 = =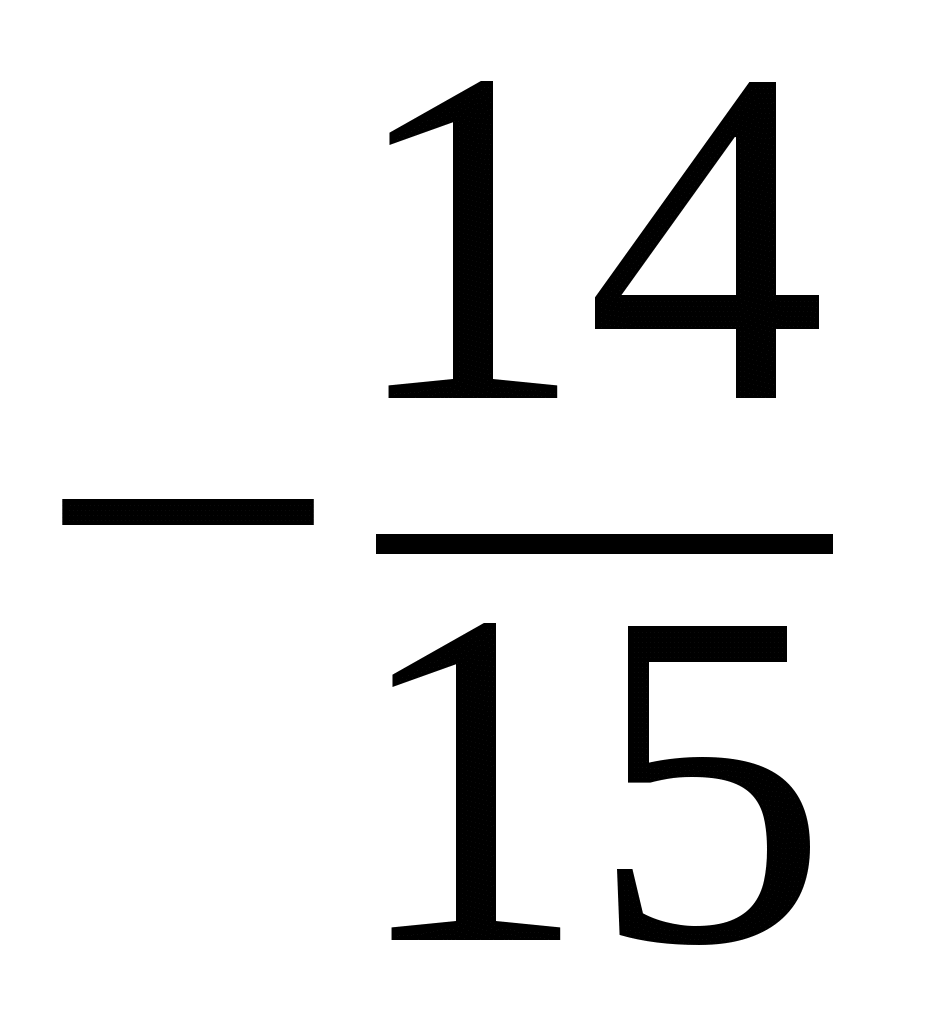 . .
Вычислить 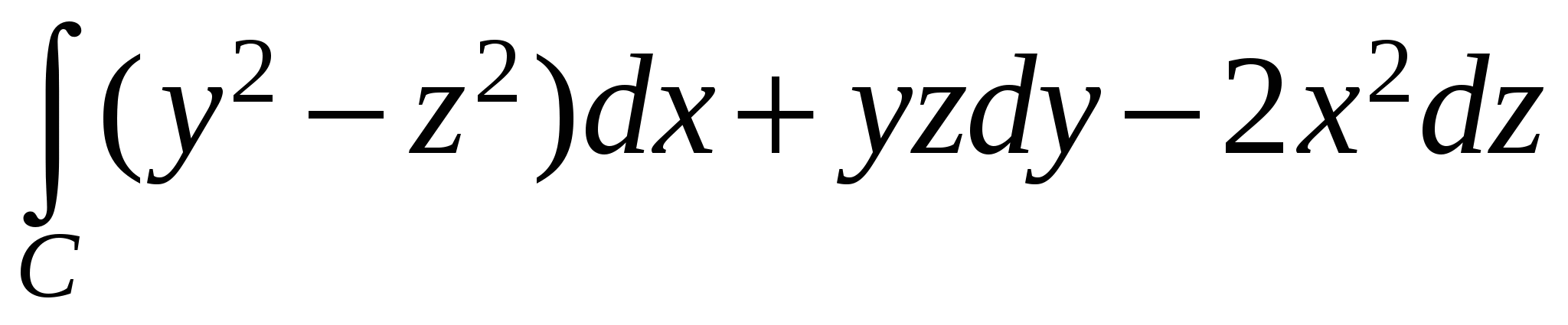 , где C – кривая , где C – кривая 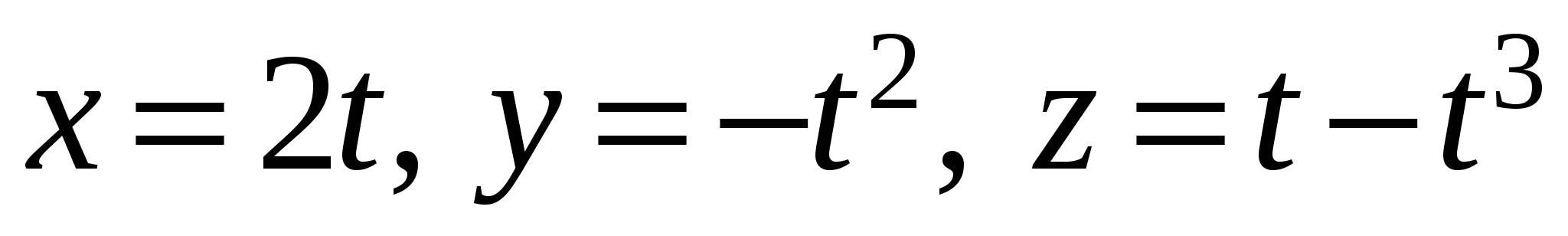 , , 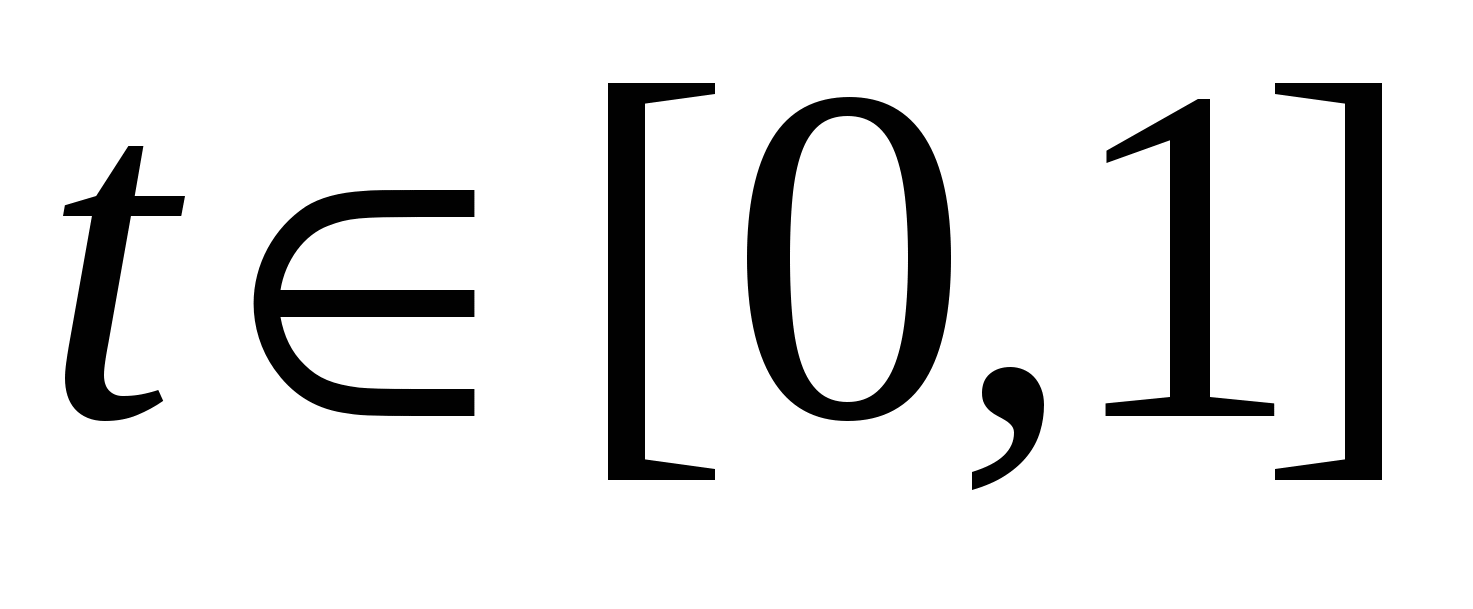 , пробегаемая в направлении возрастания параметра. , пробегаемая в направлении возрастания параметра.
3. Вычислить 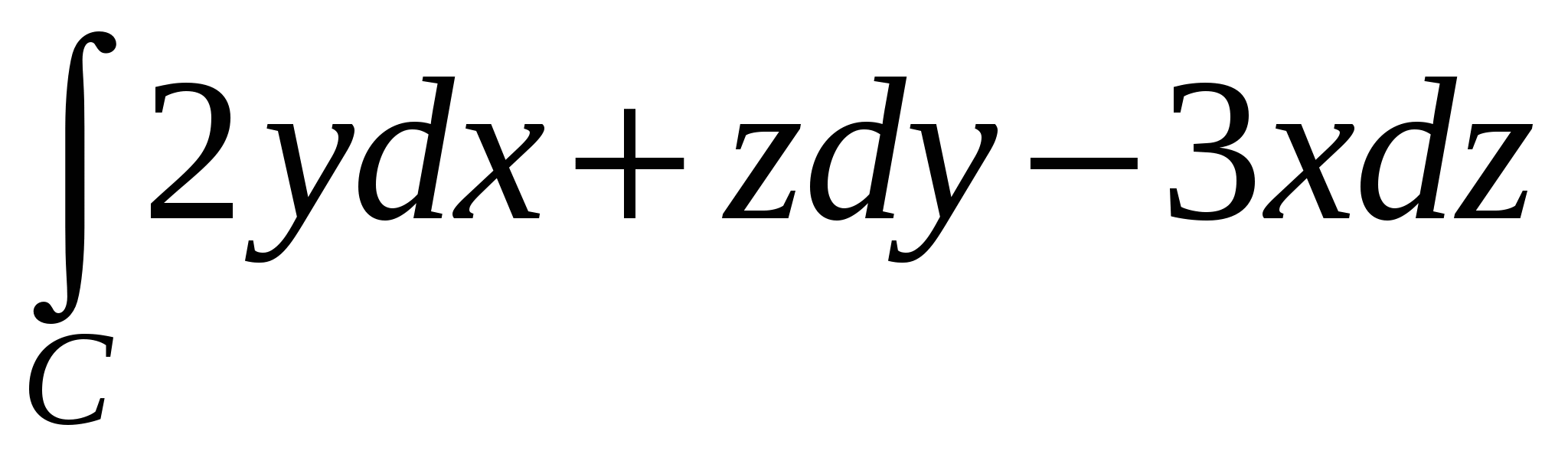 , где C – часть винтовой линии , где C – часть винтовой линии 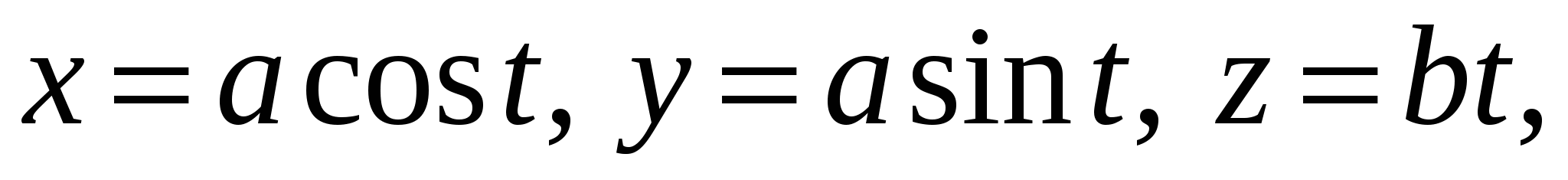 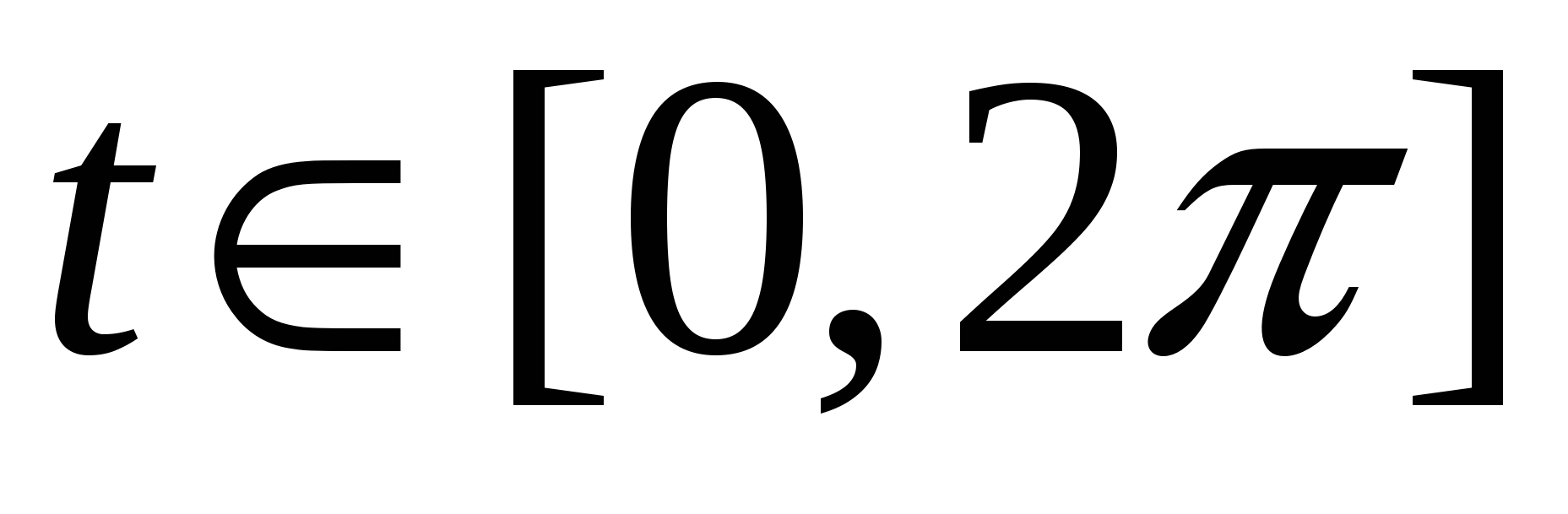 , пробегаемая в направлении возрастания параметра. , пробегаемая в направлении возрастания параметра.
Связь между криволинейным интегралом второго рода вдоль замкнутой кривой на плоскости и двойным интегралом. Формула Грина.
Пусть C – кусочно-гладкая замкнутая кривая, ограничивающая область D. На кривой C задано такое направление, что при движении в этом направлении область D остается слева. Функции 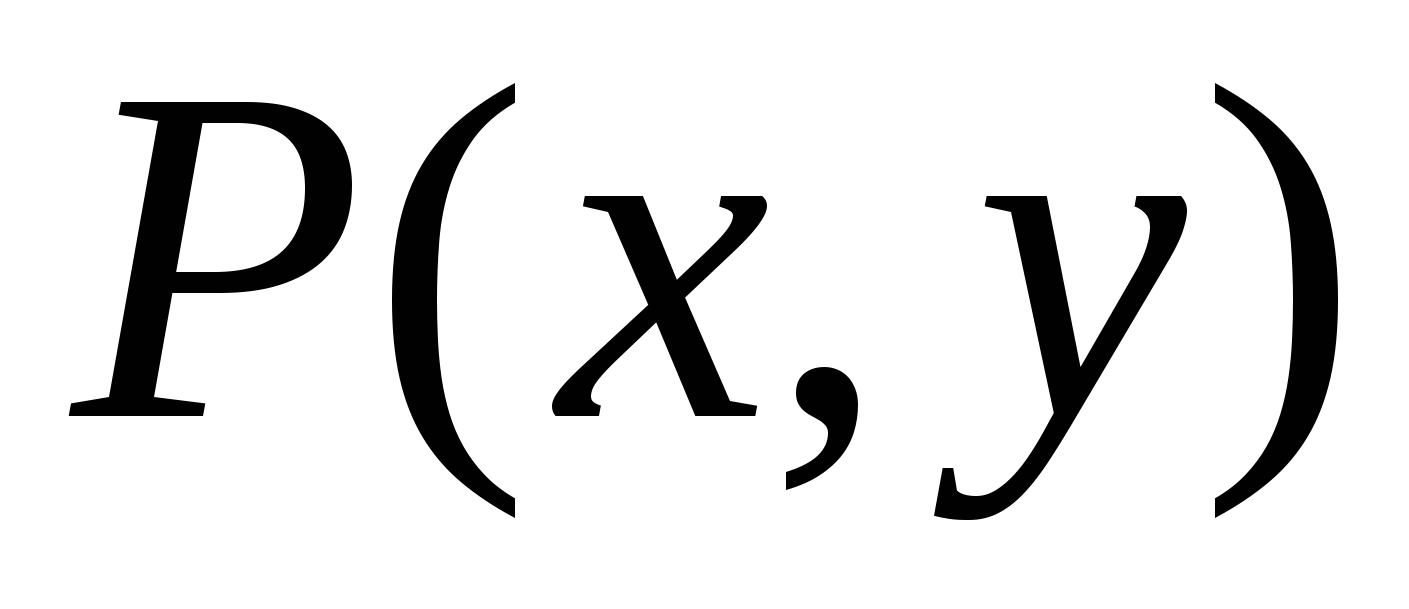 и и 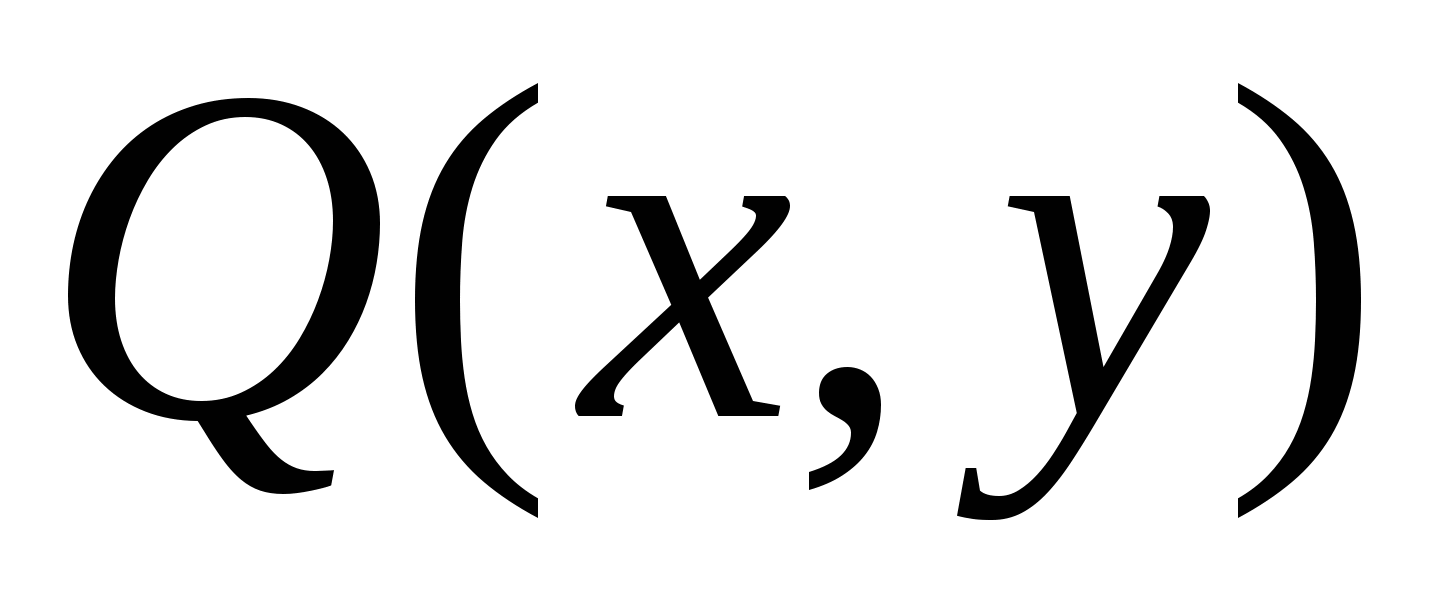 непрерывны в области D вплоть до ее границы, кроме того, функции непрерывны в области D вплоть до ее границы, кроме того, функции 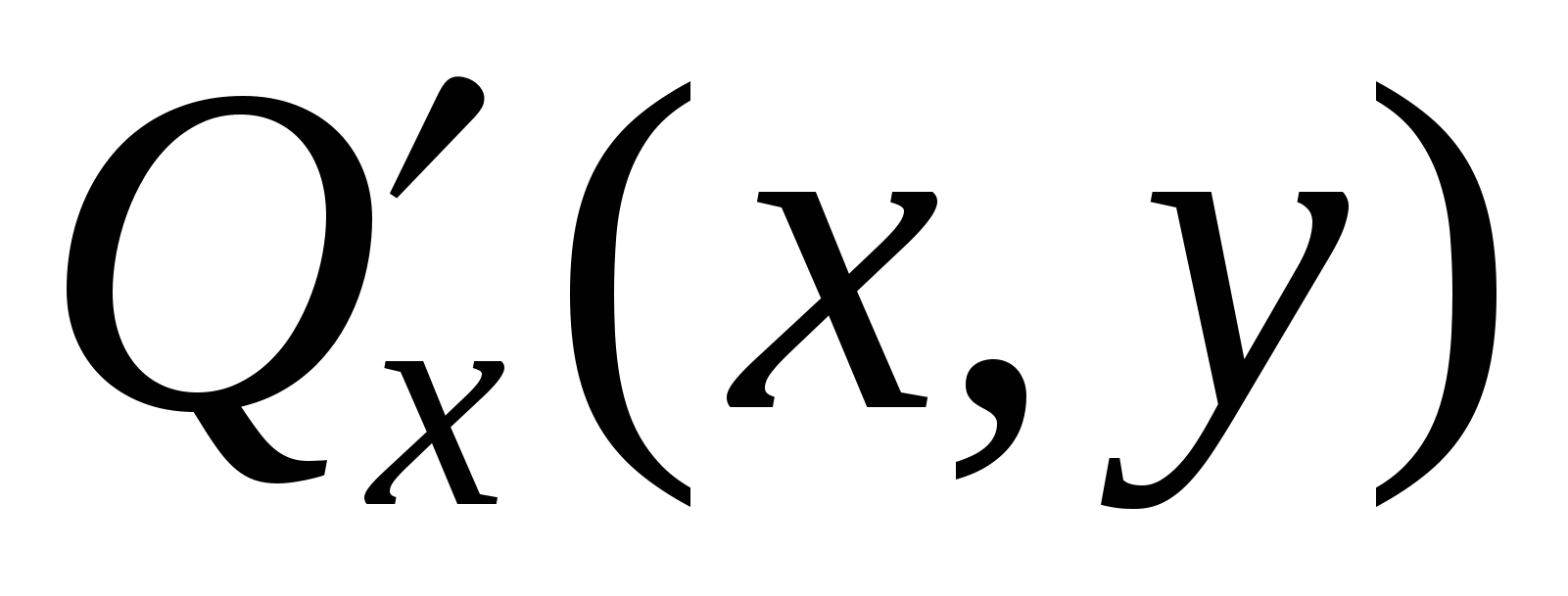 и и 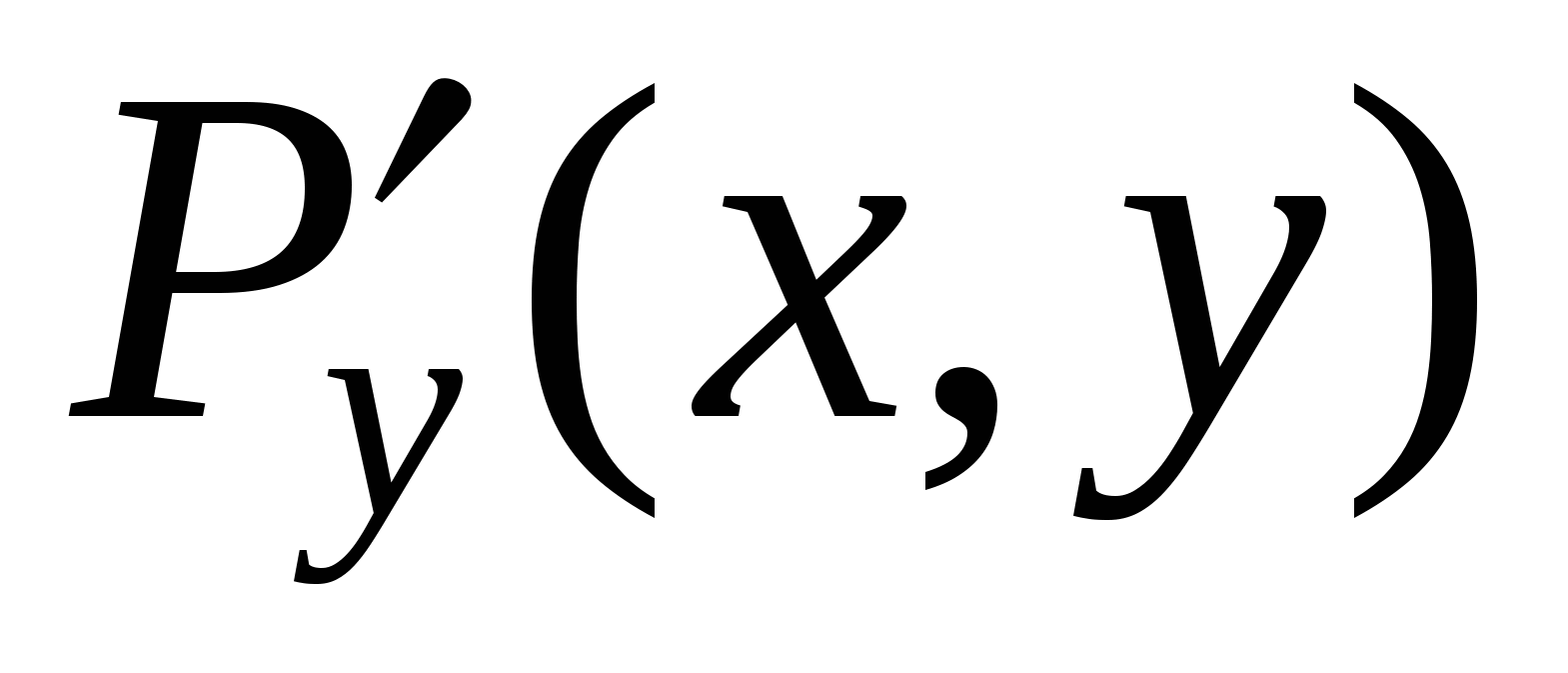 также непрерывны в D вплоть до границы. Тогда справедлива формула Грина также непрерывны в D вплоть до границы. Тогда справедлива формула Грина
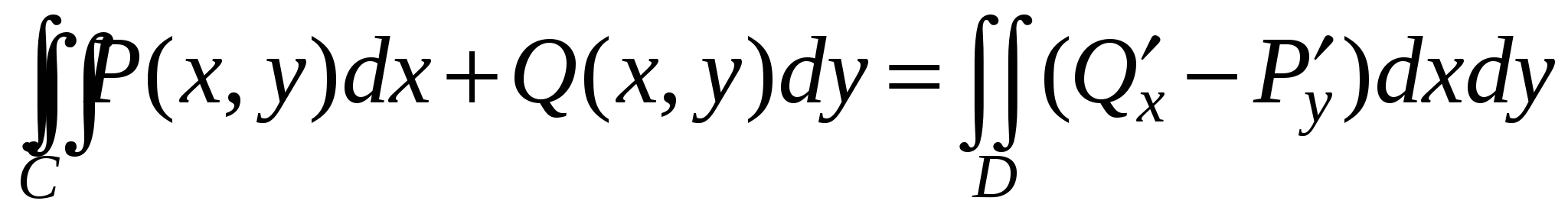 . (ФГ) . (ФГ)
1. Докажем формулу Грина сначала для случая, когда область D выпукла в направлении координатных осей, то есть, любые прямые, параллельные осям координат и пересекающие область D, пересекают ее границу либо не более, чем в двух точках, либо по отрезку прямой.
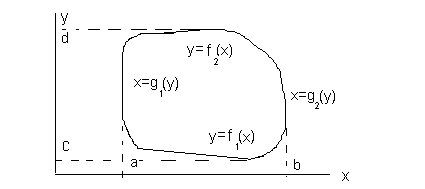
Обозначим, как это показано на рисунке, проекции области D на координатные оси 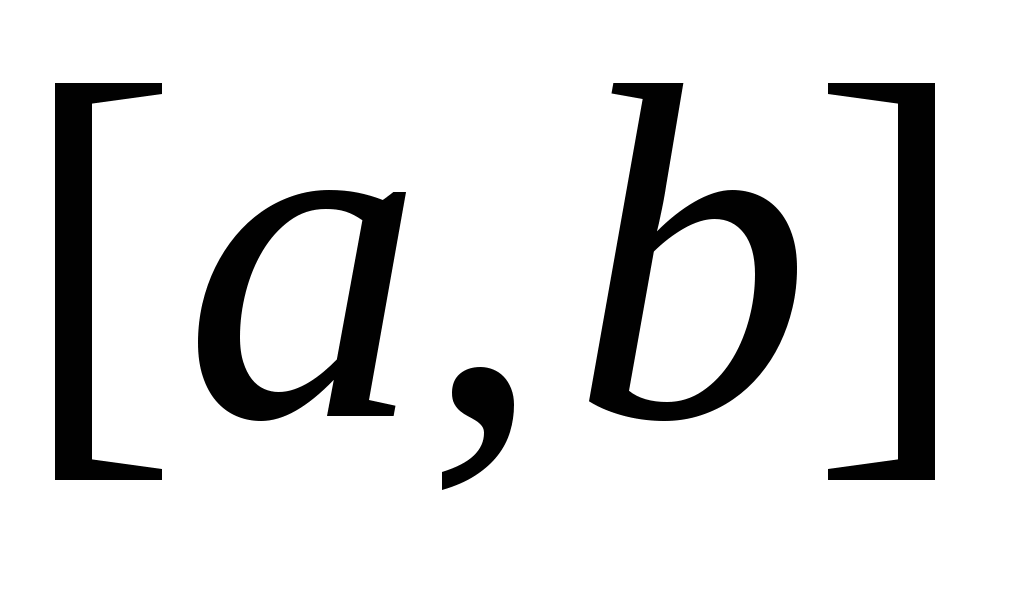 и и 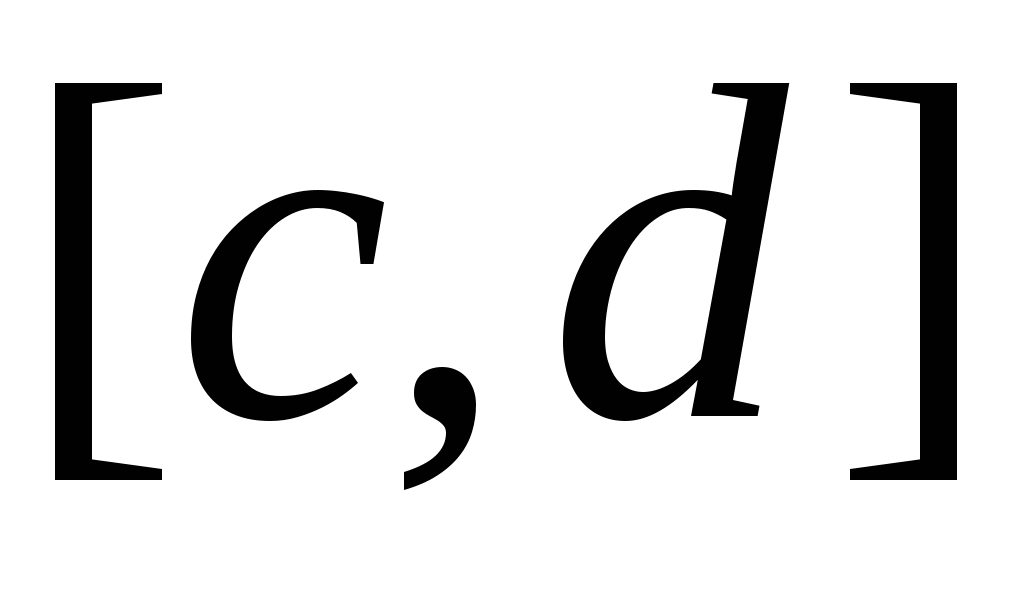 . Запишем уравнения фрагментов кривой C, однозначно проецирующихся на . Запишем уравнения фрагментов кривой C, однозначно проецирующихся на 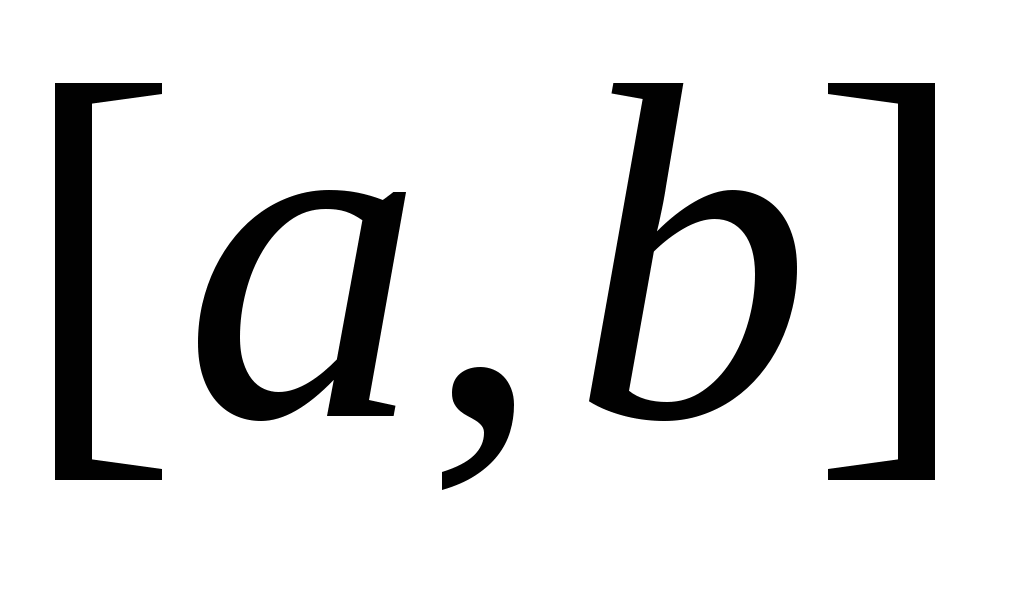 , в виде , в виде 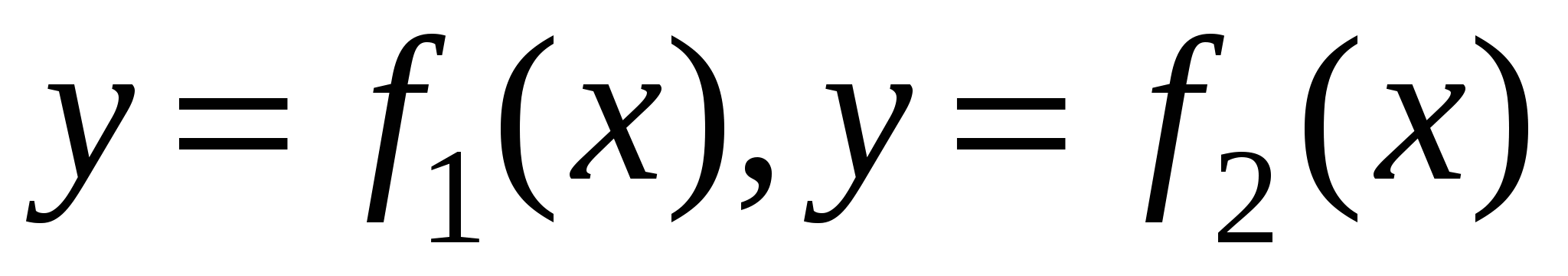 . Запишем уравнения фрагментов кривой C, однозначно проецирующихся на . Запишем уравнения фрагментов кривой C, однозначно проецирующихся на 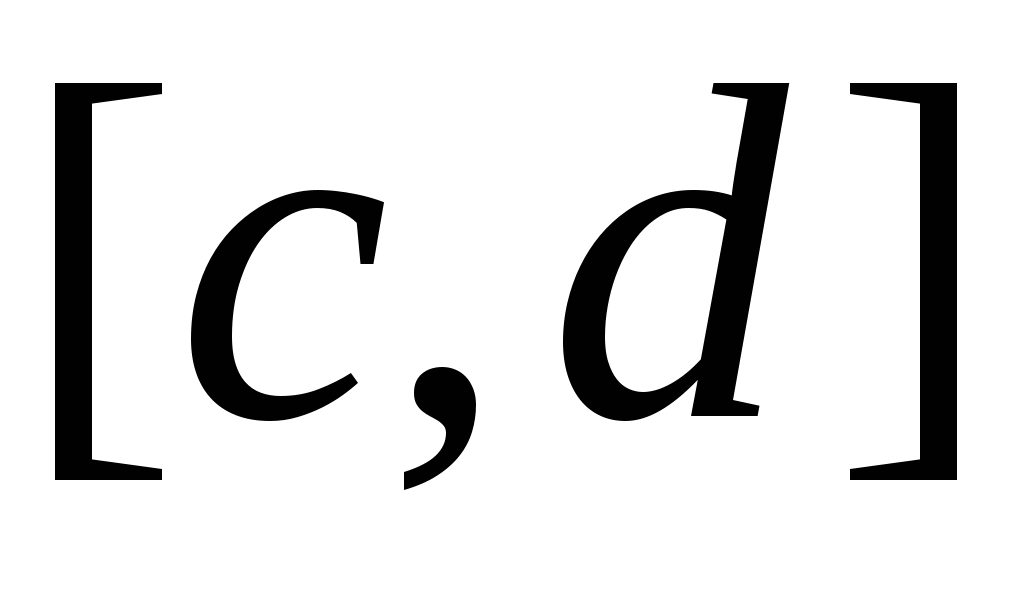 , в виде , в виде 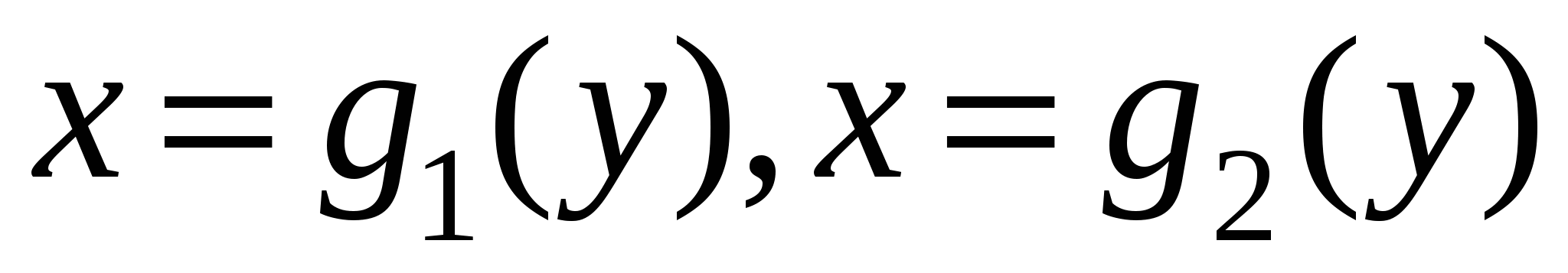 . .
Сосчитаем сначала интеграл 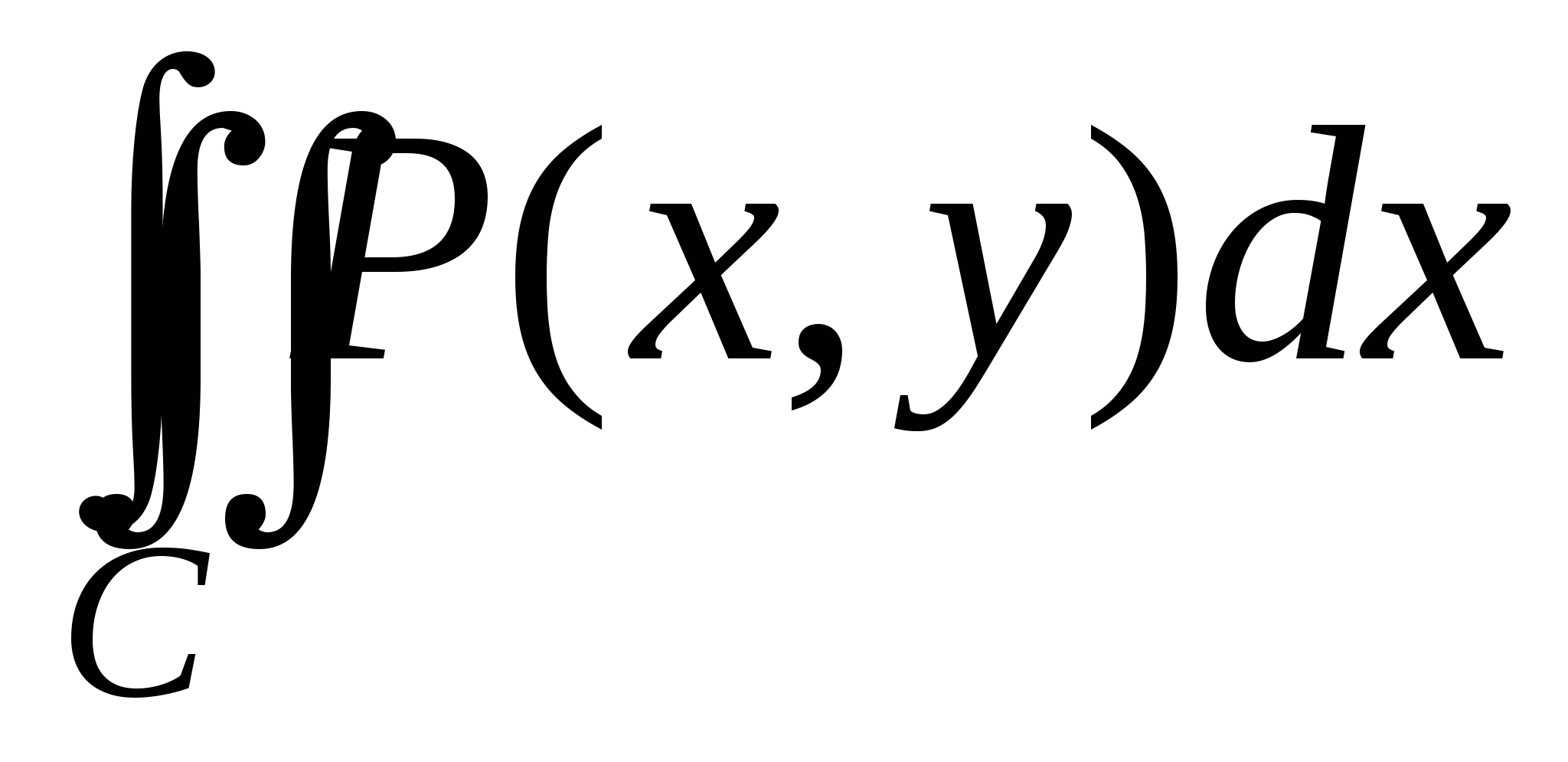 . Представим его в виде суммы криволинейных интегралов по двум фрагментам, однозначно проецирующимся на отрезок . Представим его в виде суммы криволинейных интегралов по двум фрагментам, однозначно проецирующимся на отрезок 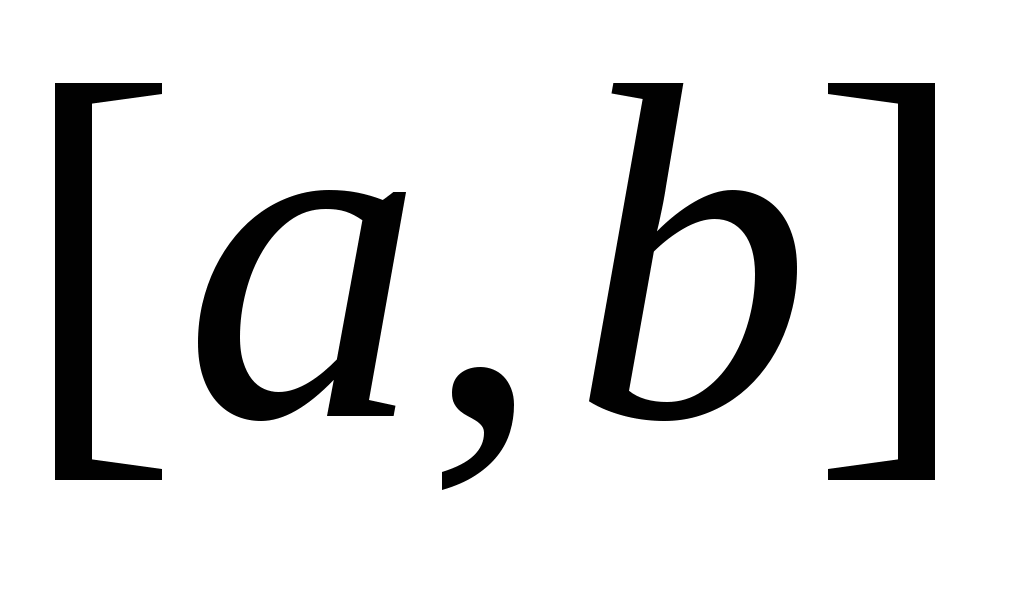 . Если на C есть еще и отрезок, параллельный оси OY, то рассматриваемый интеграл по этому отрезку равен нулю, так как . Если на C есть еще и отрезок, параллельный оси OY, то рассматриваемый интеграл по этому отрезку равен нулю, так как 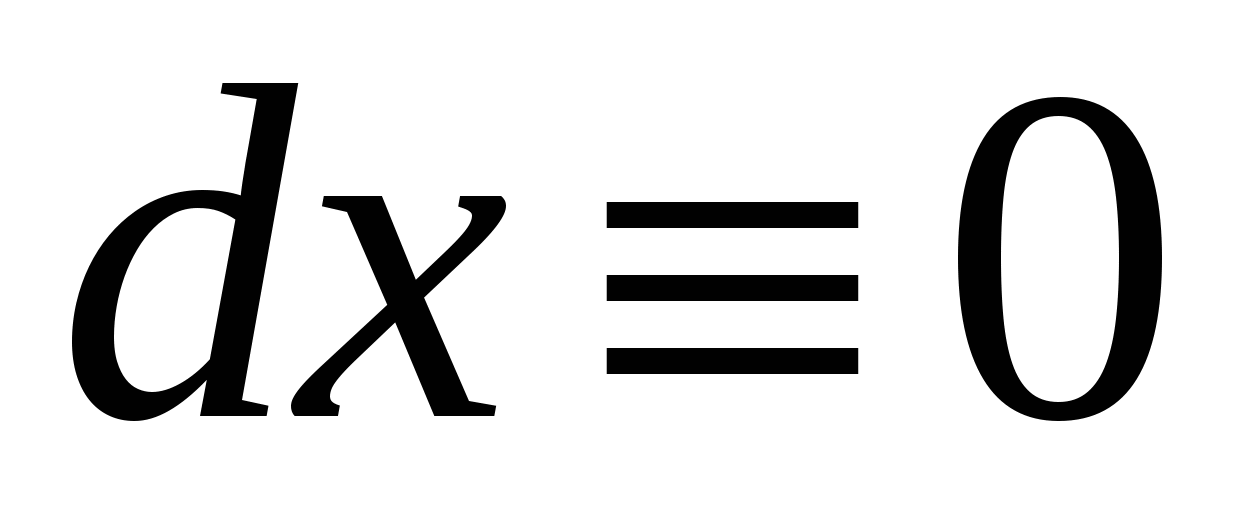 . На первом фрагменте мы получим параметризацию . На первом фрагменте мы получим параметризацию 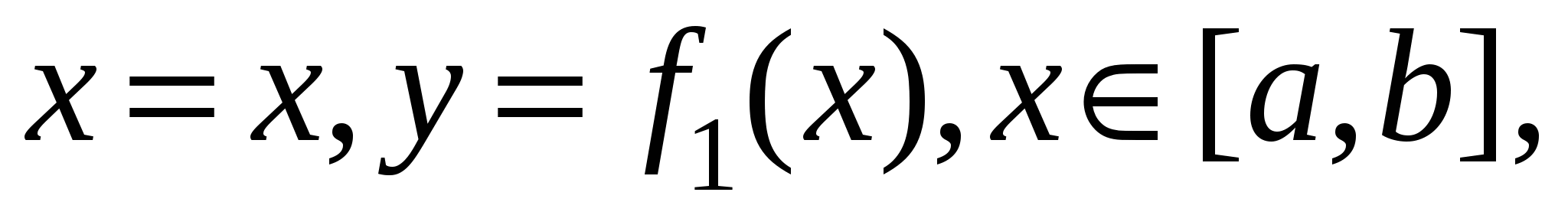 причем в соответствии с заданием направления движения параметр причем в соответствии с заданием направления движения параметр 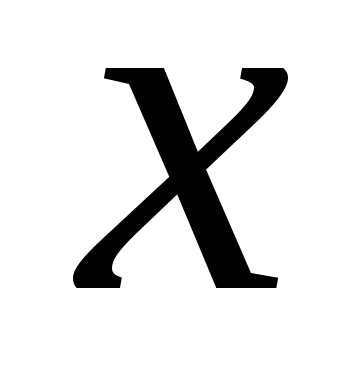 должен возрастать, когда мы движемся по этому фрагменту в заданном направлении. На втором фрагменте имеем параметризацию должен возрастать, когда мы движемся по этому фрагменту в заданном направлении. На втором фрагменте имеем параметризацию 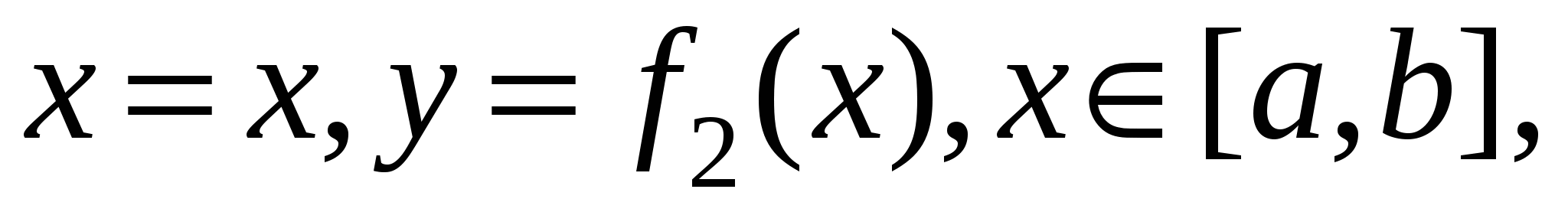 причем параметр причем параметр 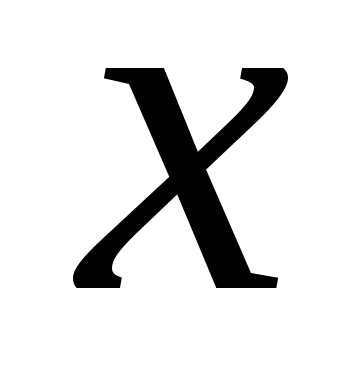 убывает, когда мы движемся по второму фрагменту в заданном направлении. Таким образом, убывает, когда мы движемся по второму фрагменту в заданном направлении. Таким образом,
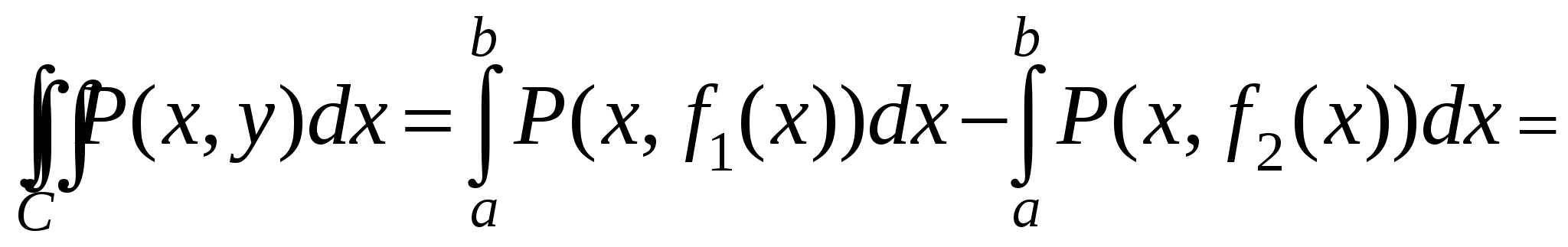 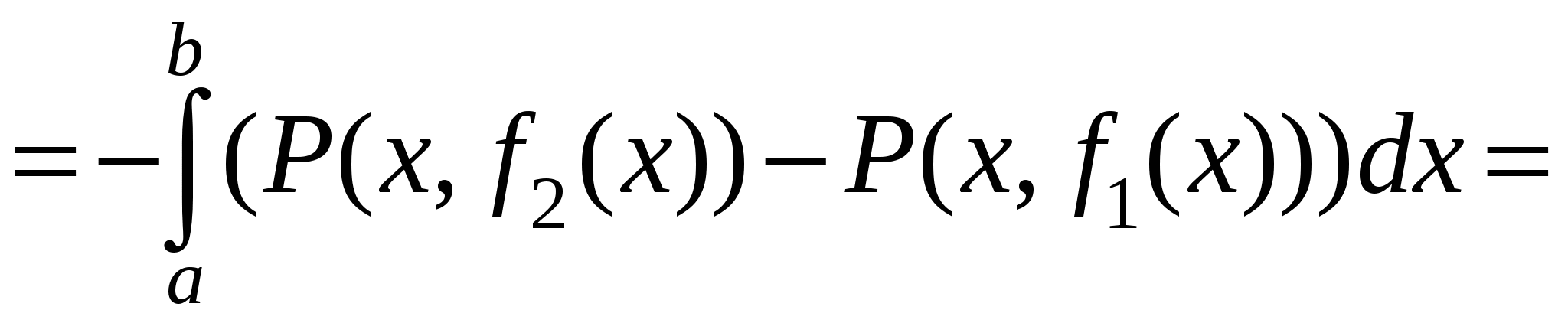
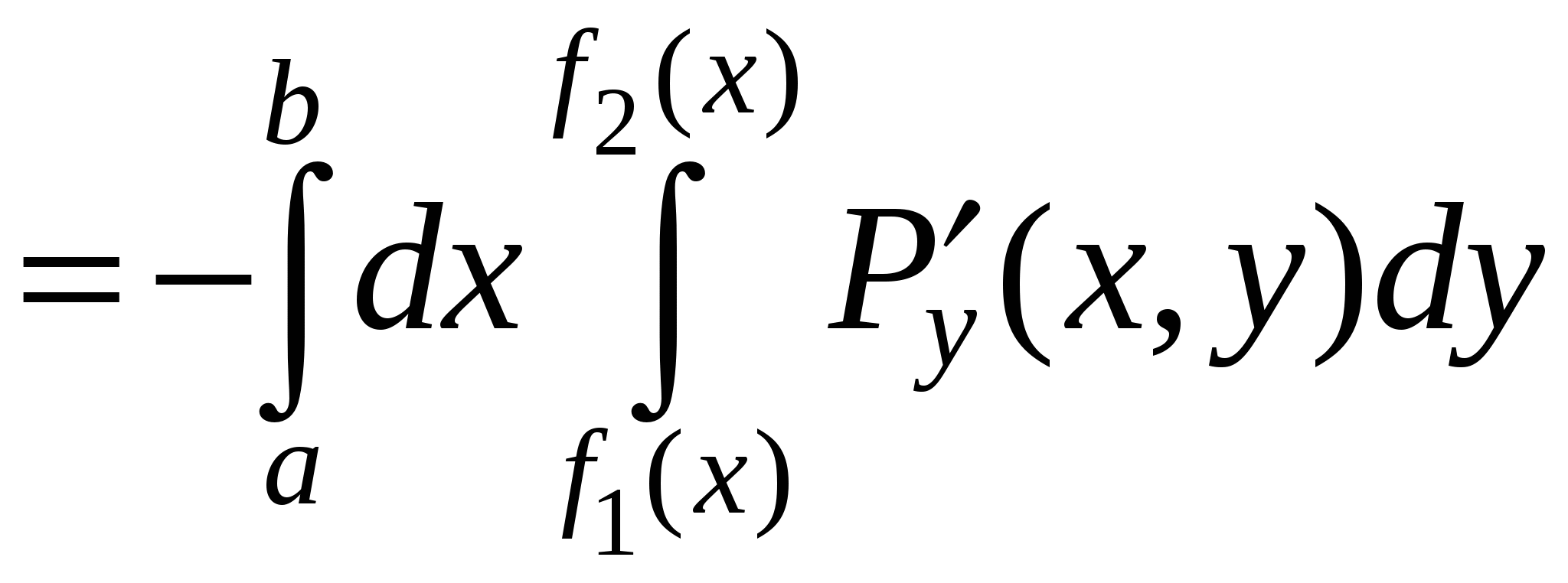 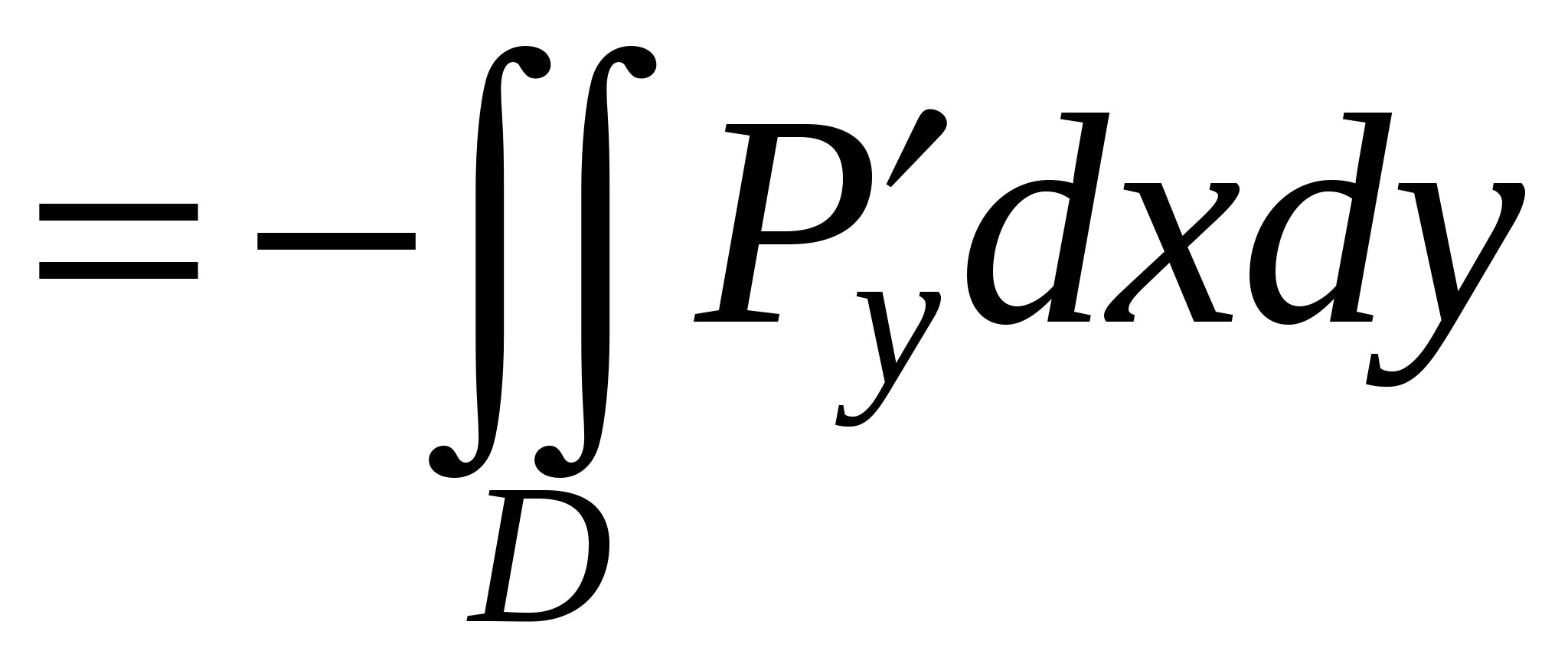 . .
Для того, чтобы сосчитать интеграл 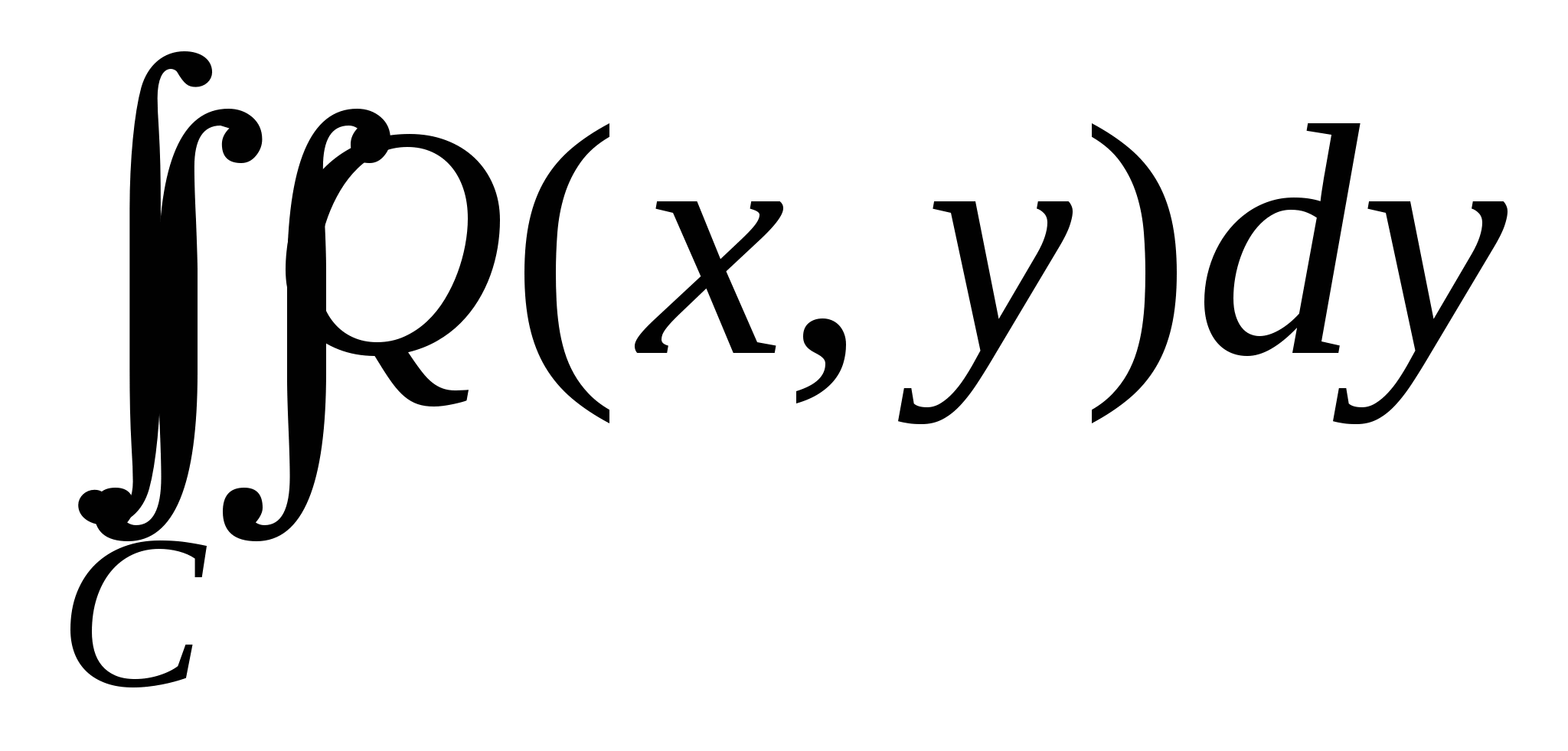 , разобьем С на фрагменты, однозначно проецирующиеся на отрезок , разобьем С на фрагменты, однозначно проецирующиеся на отрезок 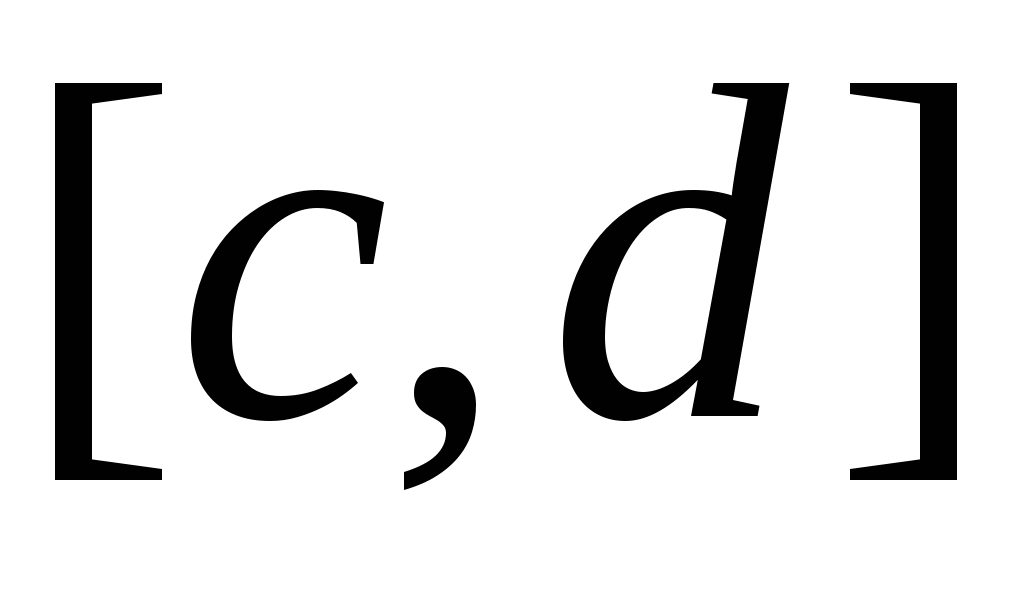 . В случае, когда на C есть отрезок, параллельный OX, то на нем . В случае, когда на C есть отрезок, параллельный OX, то на нем 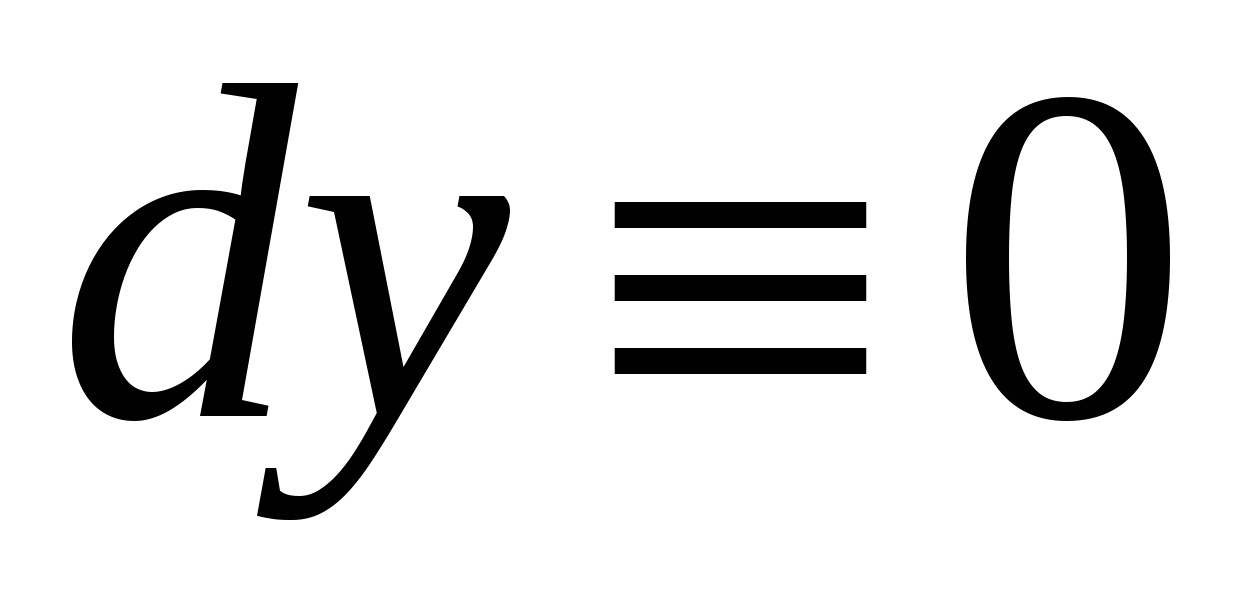 , и значит рассматриваемый интеграл вдоль этого отрезка обращается в ноль. На первом фрагменте введем параметризацию , и значит рассматриваемый интеграл вдоль этого отрезка обращается в ноль. На первом фрагменте введем параметризацию 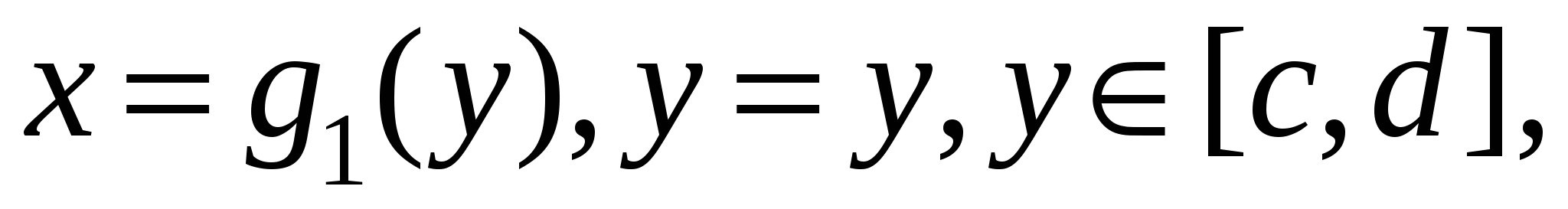 причем при заданном направлении движения параметр причем при заданном направлении движения параметр 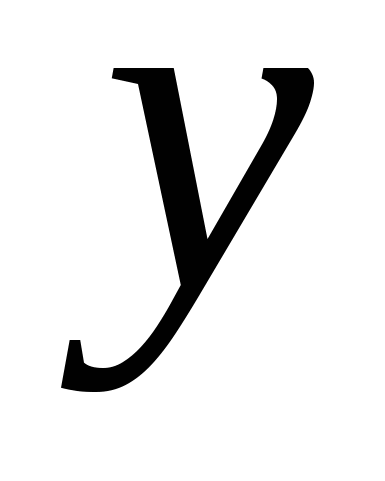 должен убывать при проходе по этому фрагменту. На втором фрагменте параметризация должен убывать при проходе по этому фрагменту. На втором фрагменте параметризация 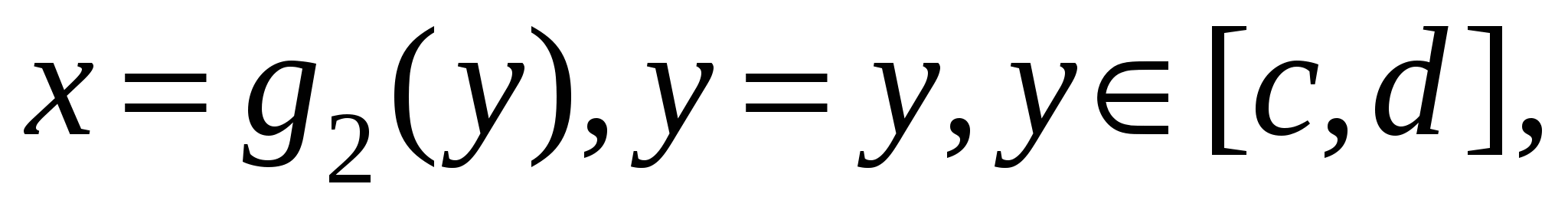 и параметр и параметр 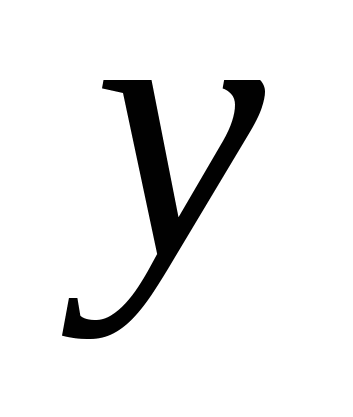 возрастает при проходе по фрагменту в заданном направлении. Следовательно, возрастает при проходе по фрагменту в заданном направлении. Следовательно,
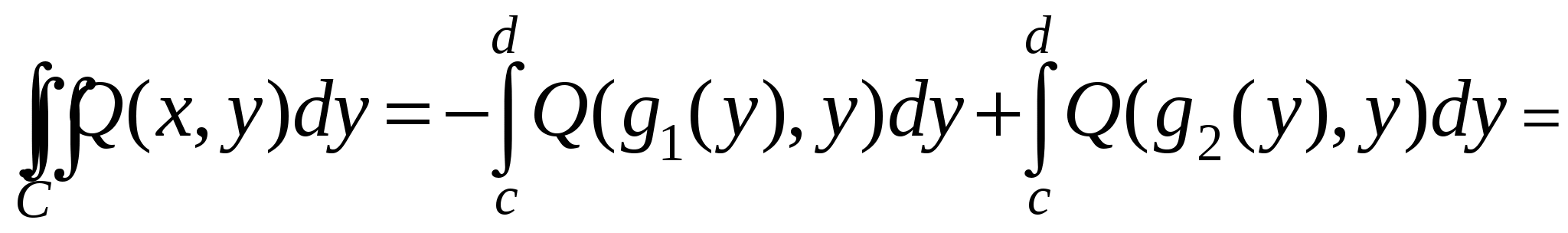 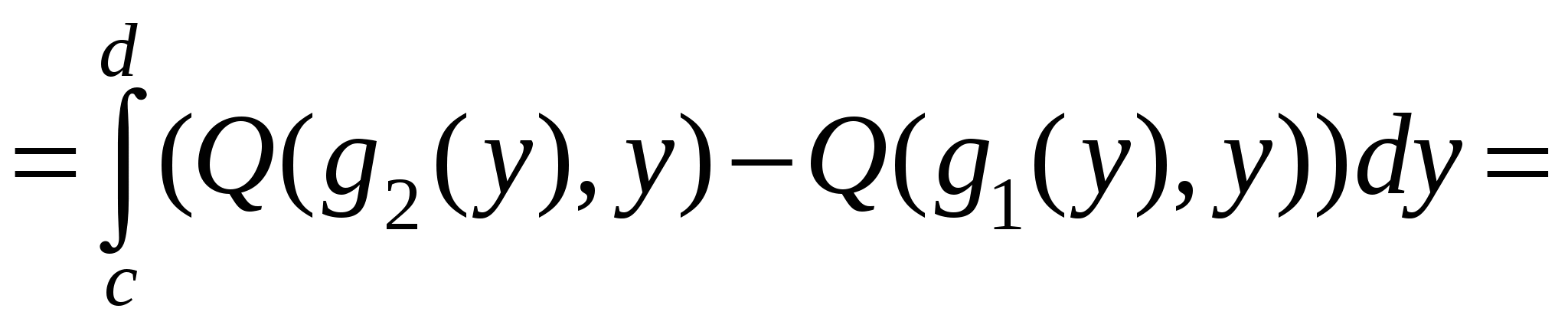
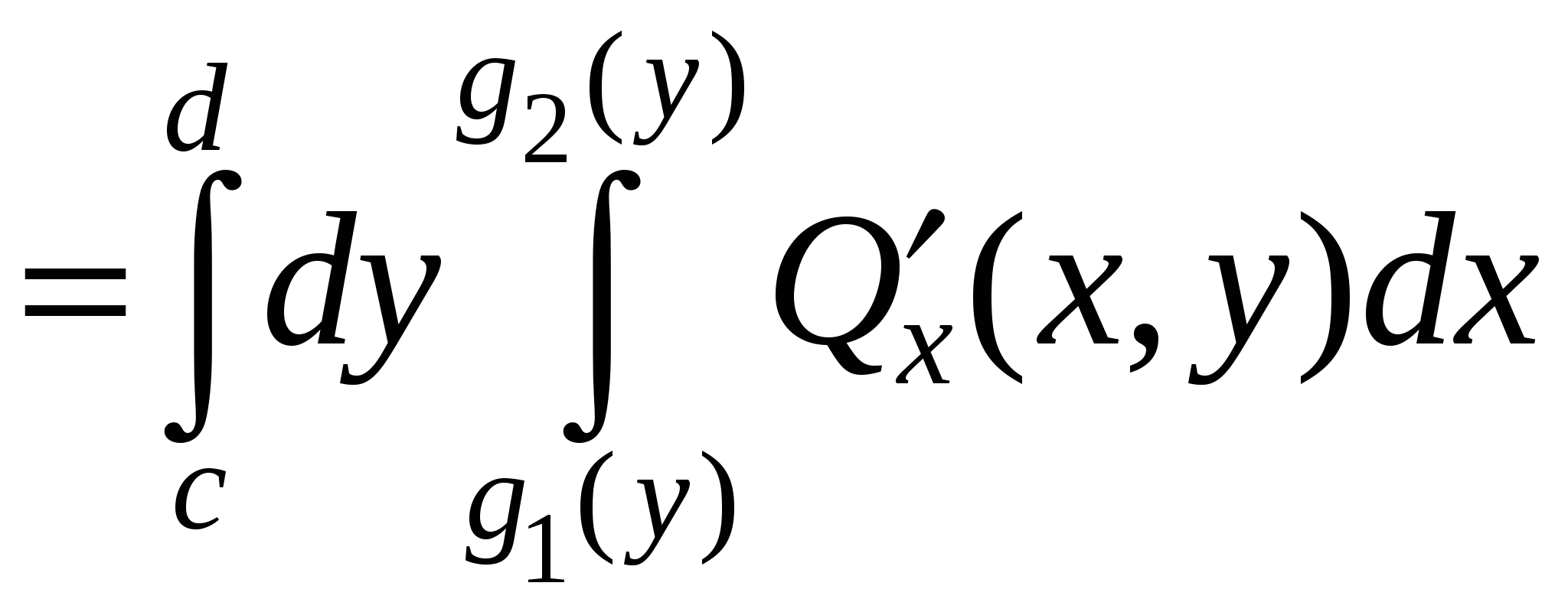 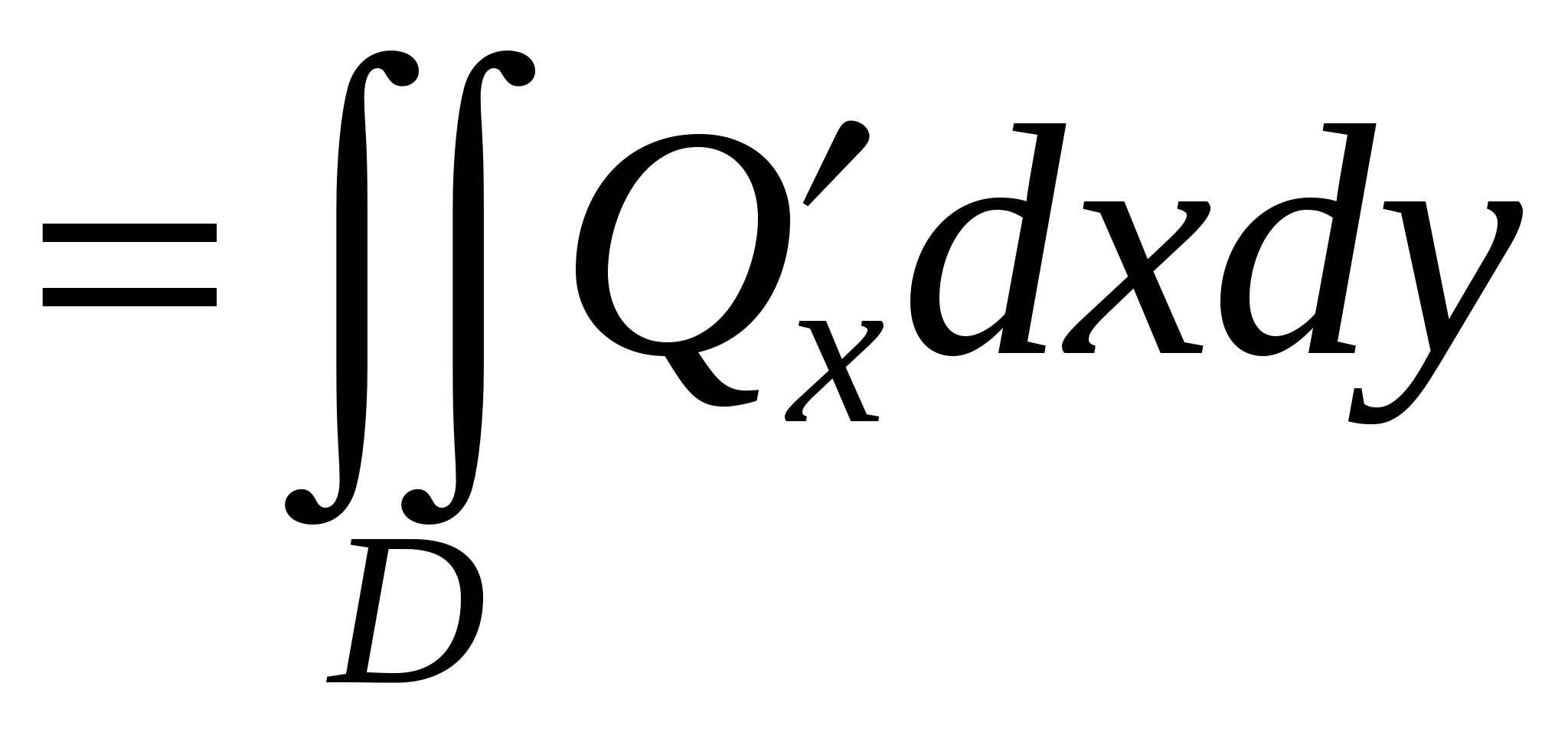 . .
Суммируя, получим формулу Грина для областей указанного вида.
2. Для доказательства справедливости формулы Грина для области D общего вида разобьем область D на конечное число областей 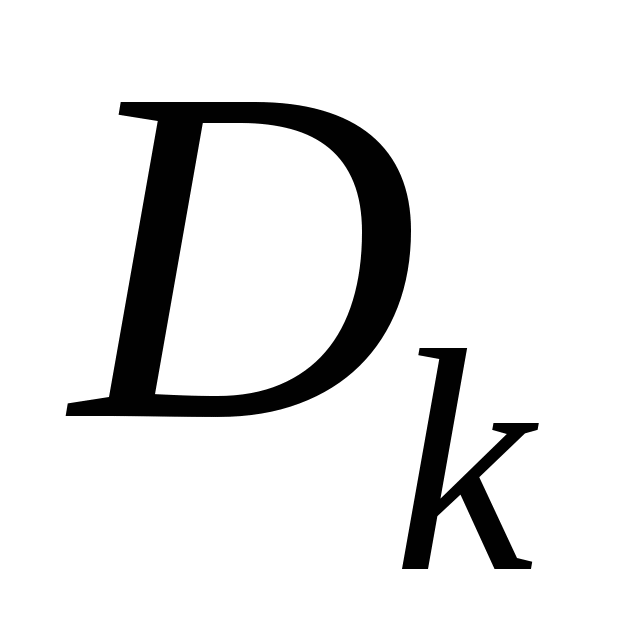 , , 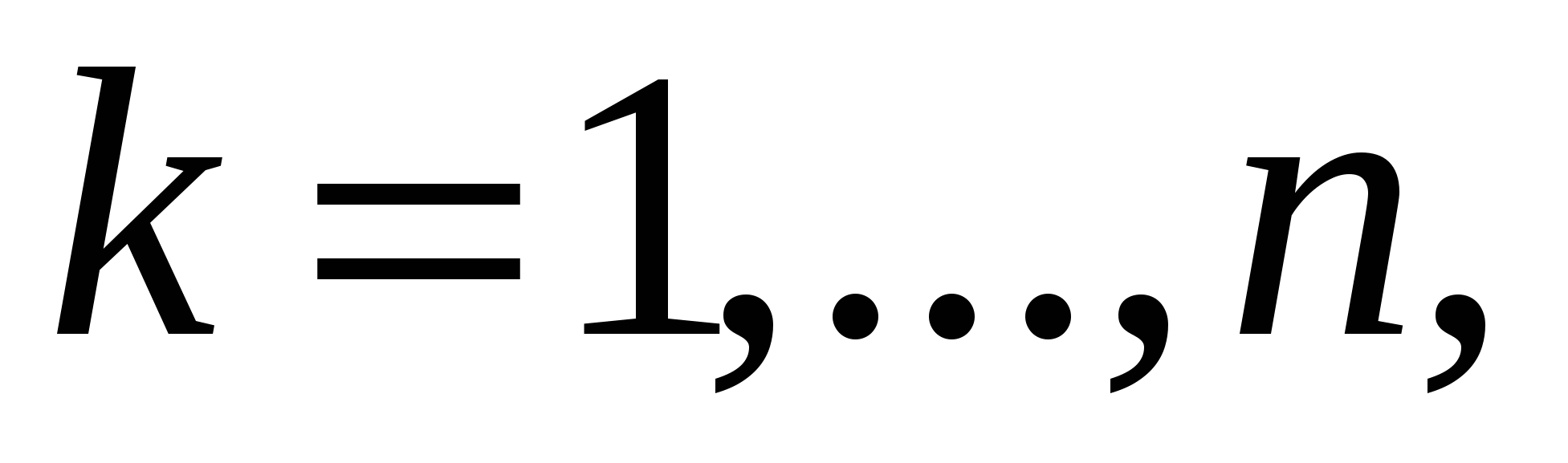 рассмотренного выше вида проведением прямых, параллельных осям OX и OY. рассмотренного выше вида проведением прямых, параллельных осям OX и OY.
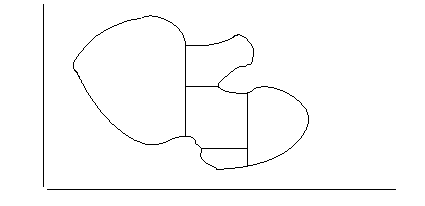
Границы полученных таким образом областей 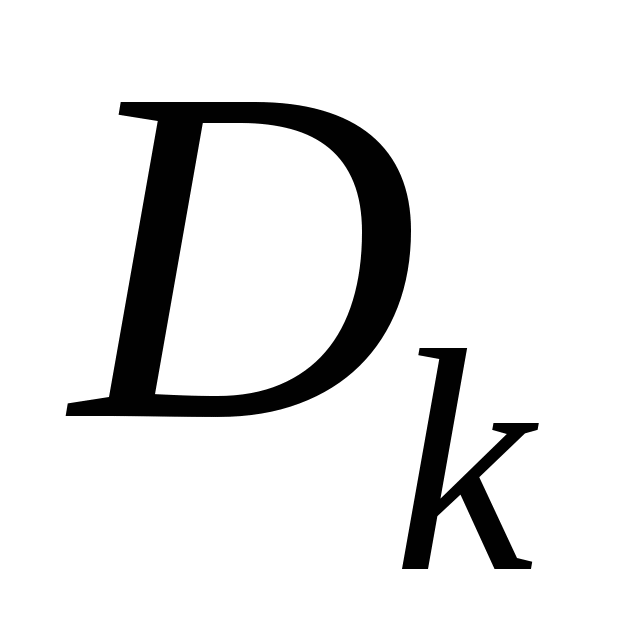 , , 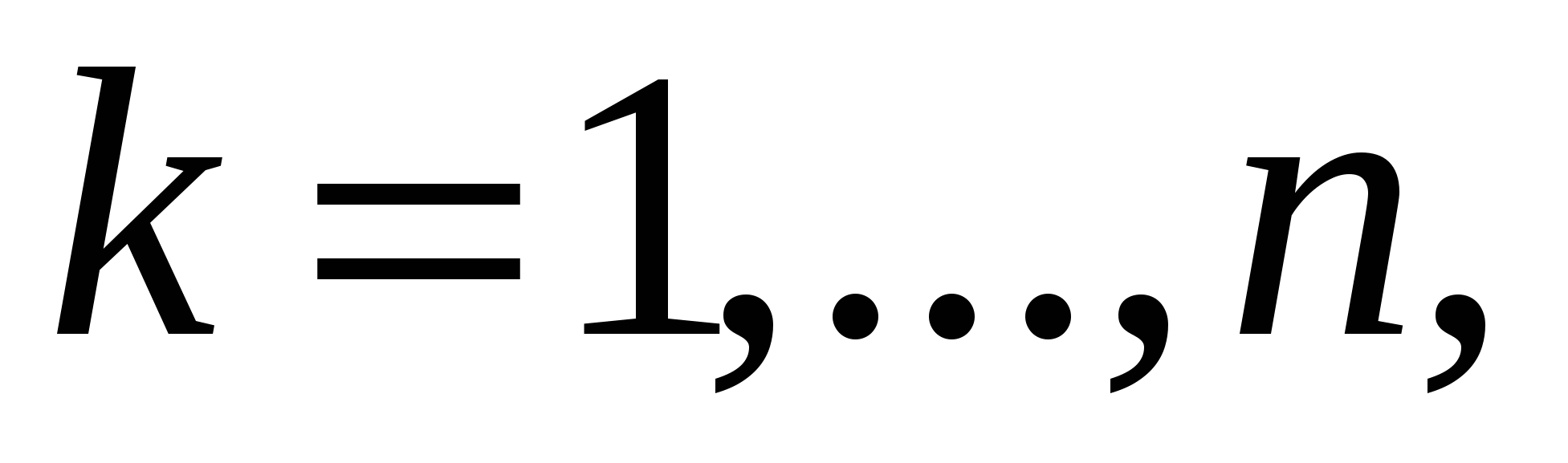 состоят из фрагментов кривой C и из отрезков, параллельных координатным осям. Заметим, что при последовательном обходе границ состоят из фрагментов кривой C и из отрезков, параллельных координатным осям. Заметим, что при последовательном обходе границ 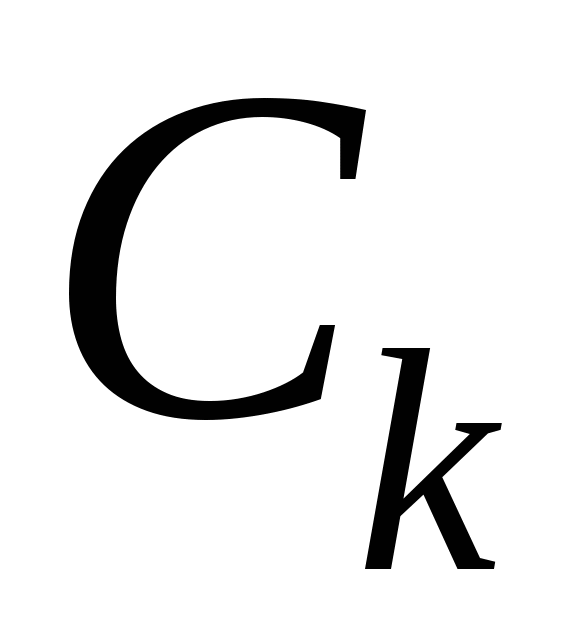 , , 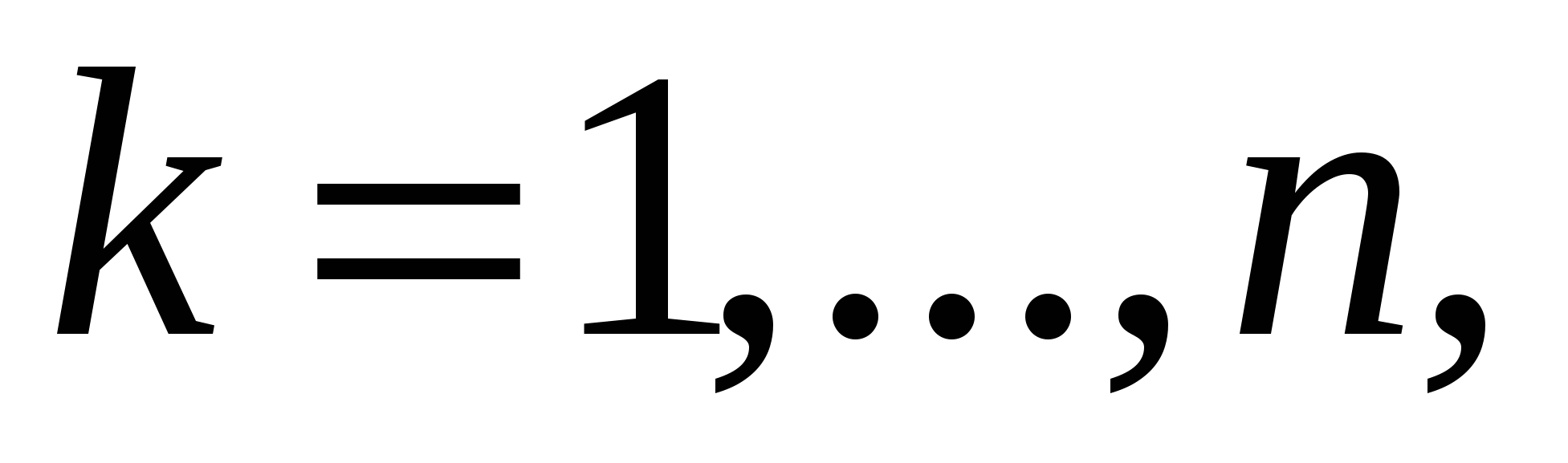 всех полученных областей всех полученных областей 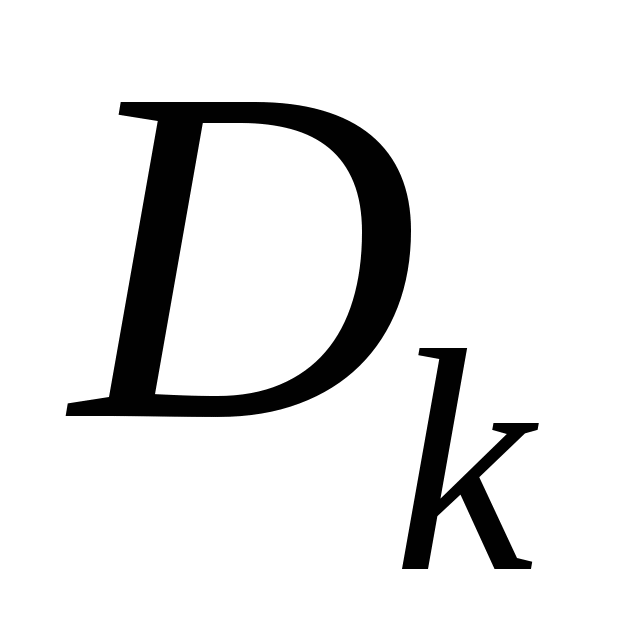 , так, чтобы область , так, чтобы область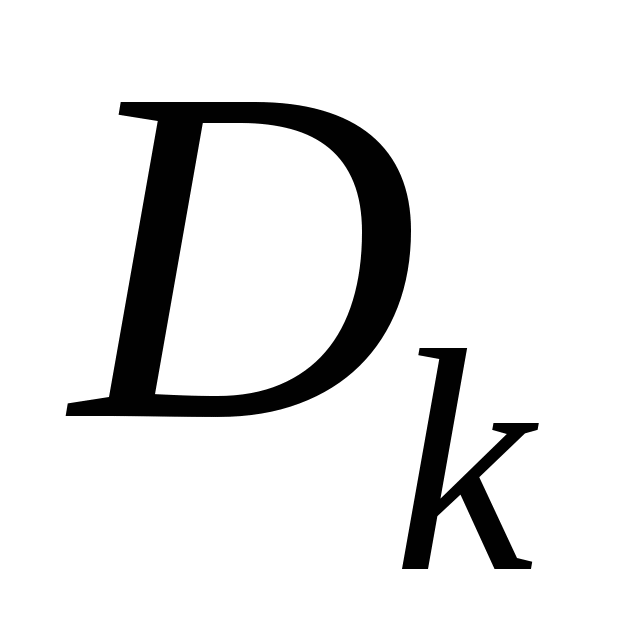 находилась слева, каждый из отрезков, параллельных координатным осям, образовавшихся при разрезании D, проходится дважды: в ту и в другую стороны. Значит, при вычислении криволинейного интеграла находилась слева, каждый из отрезков, параллельных координатным осям, образовавшихся при разрезании D, проходится дважды: в ту и в другую стороны. Значит, при вычислении криволинейного интеграла 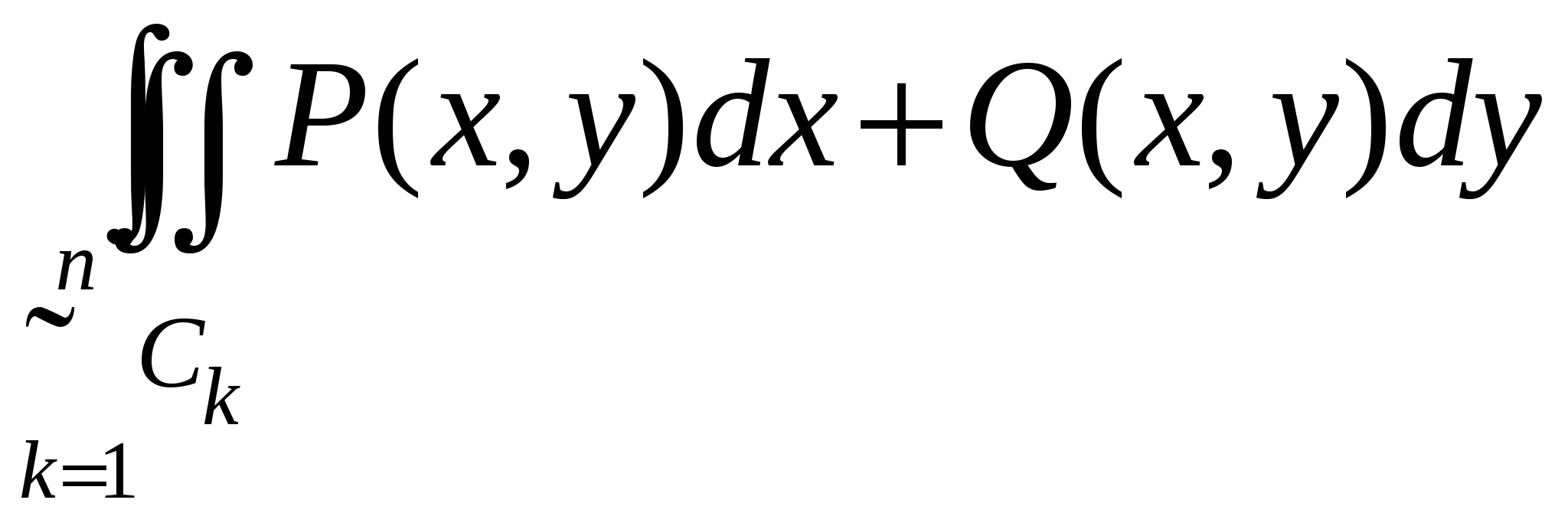 мы получим взаимное уничтожение интегралов вдоль прямолинейных отрезков внутри D. мы получим взаимное уничтожение интегралов вдоль прямолинейных отрезков внутри D.
Следовательно, применяя к каждой из областей 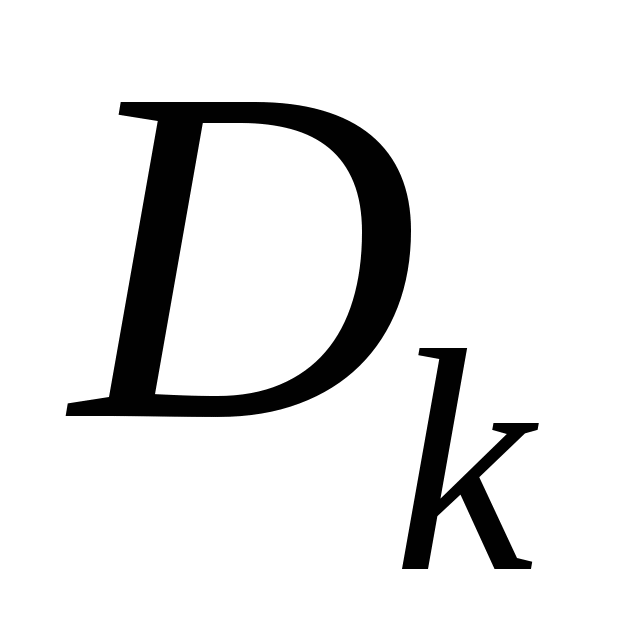 , , 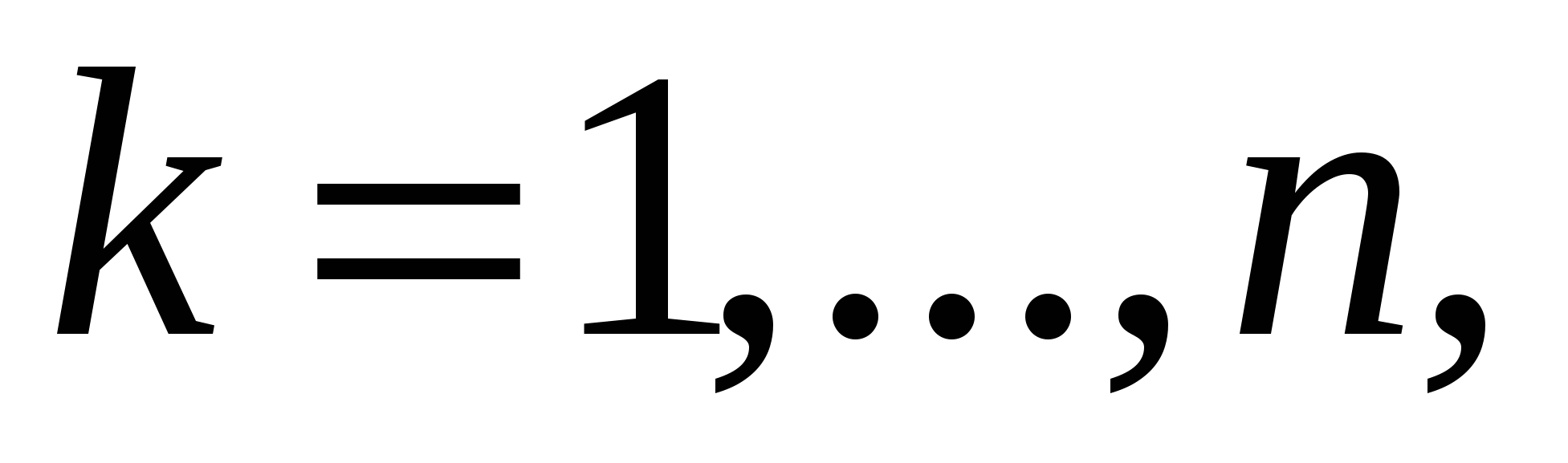 формулу Грина, получим формулу Грина, получим
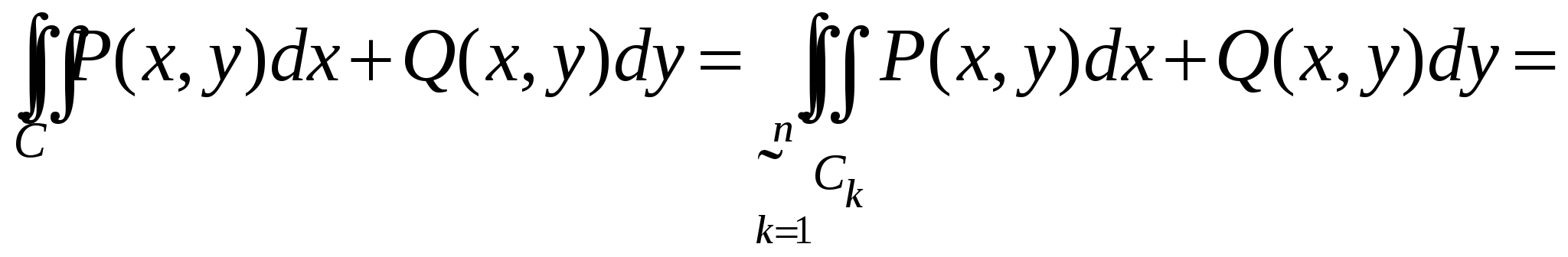 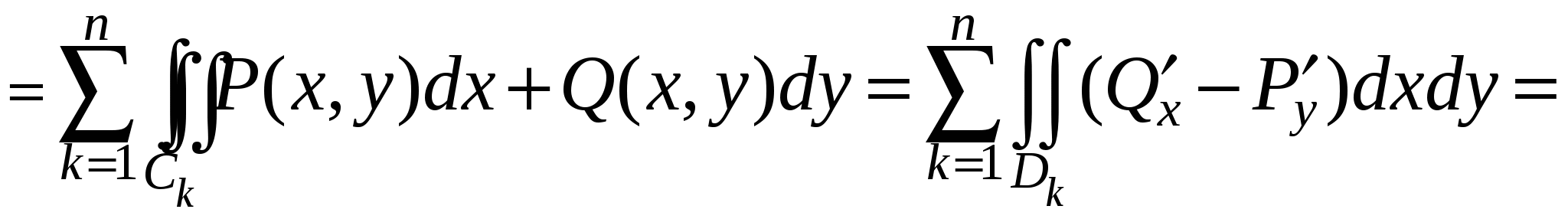 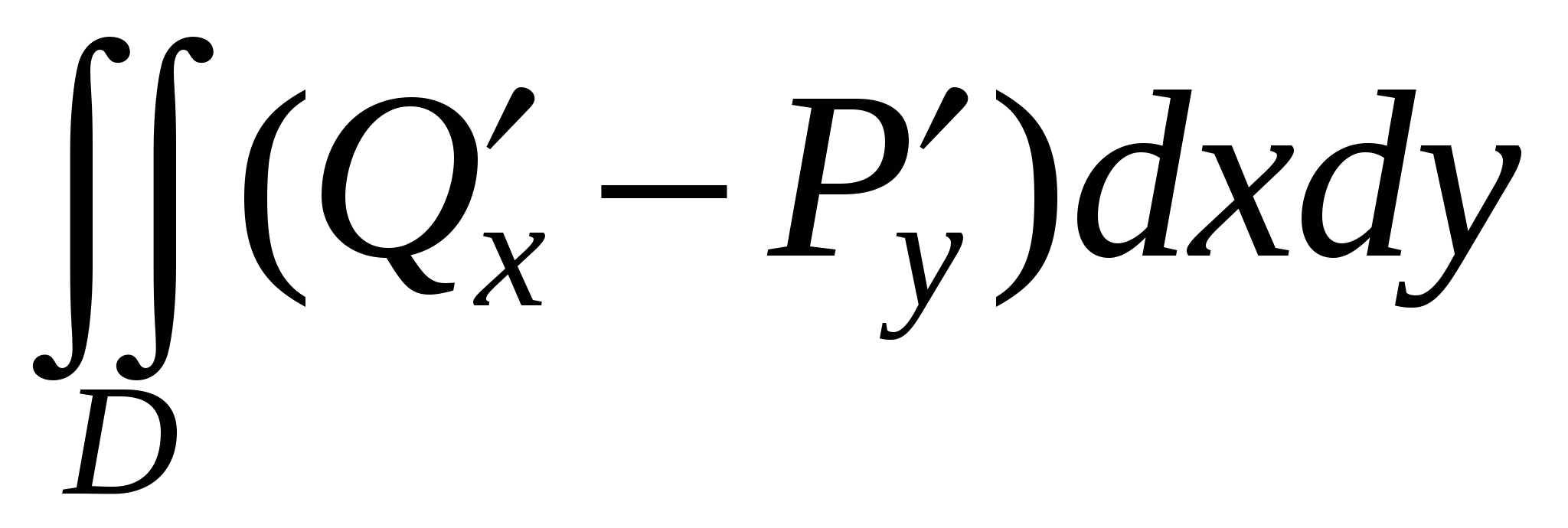 . .
Условие независимости криволинейного интеграла второго рода от пути интегрирования на плоскости.
В общем случае криволинейный интеграл  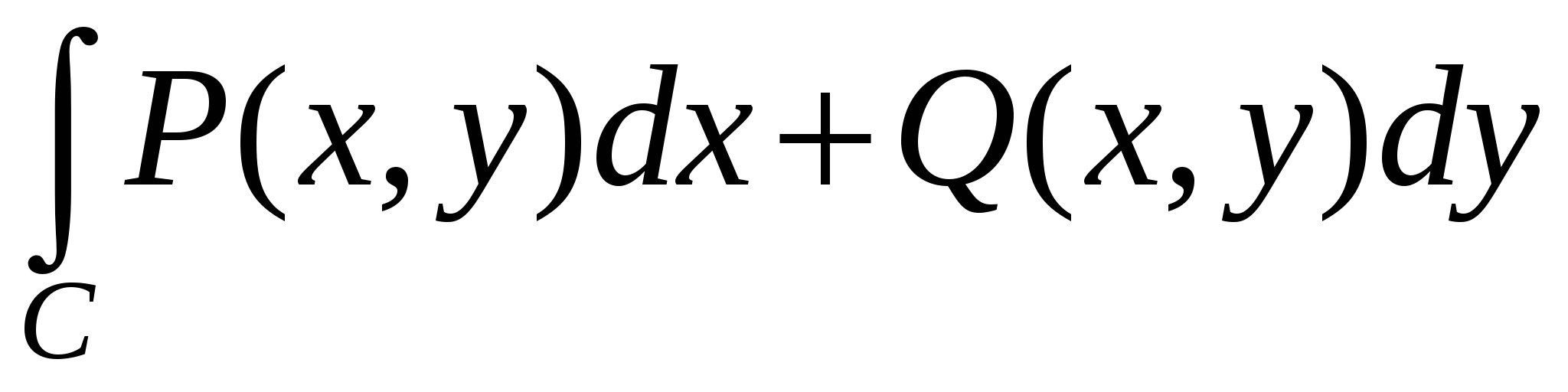 , где кривая C соединяет точки A и B на плоскости XY, зависит от пути C. Выясним, каким условиям должны удовлетворять функции , где кривая C соединяет точки A и B на плоскости XY, зависит от пути C. Выясним, каким условиям должны удовлетворять функции 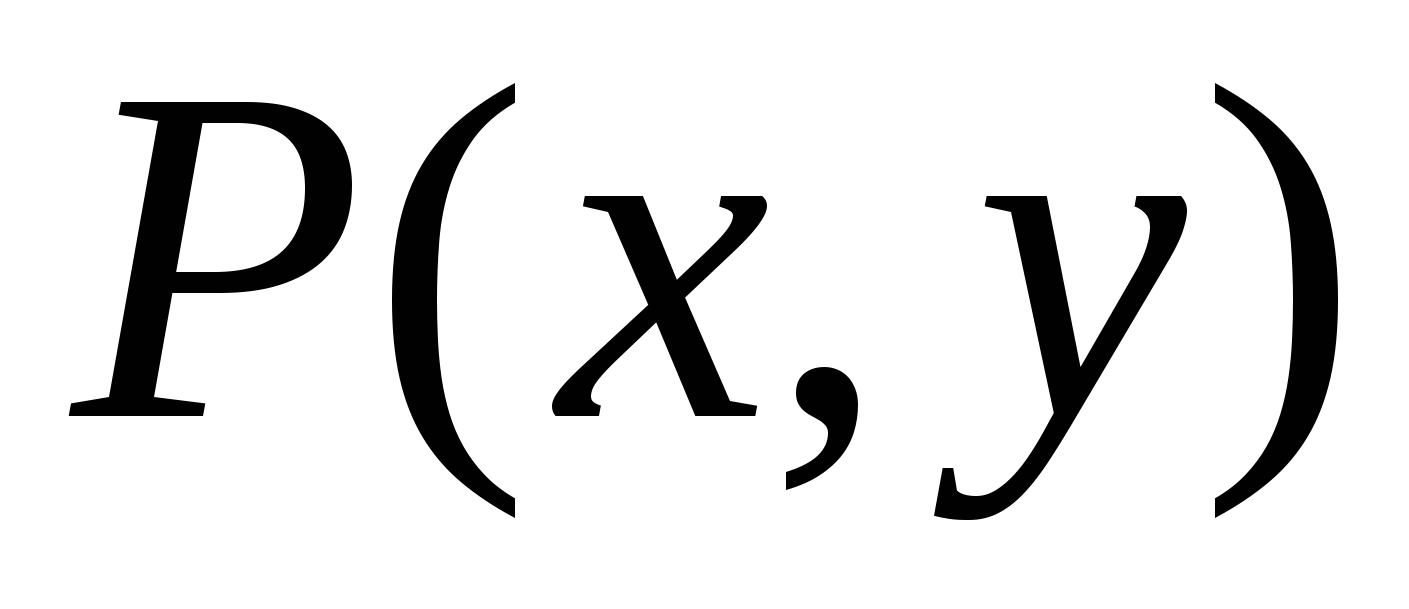 и и 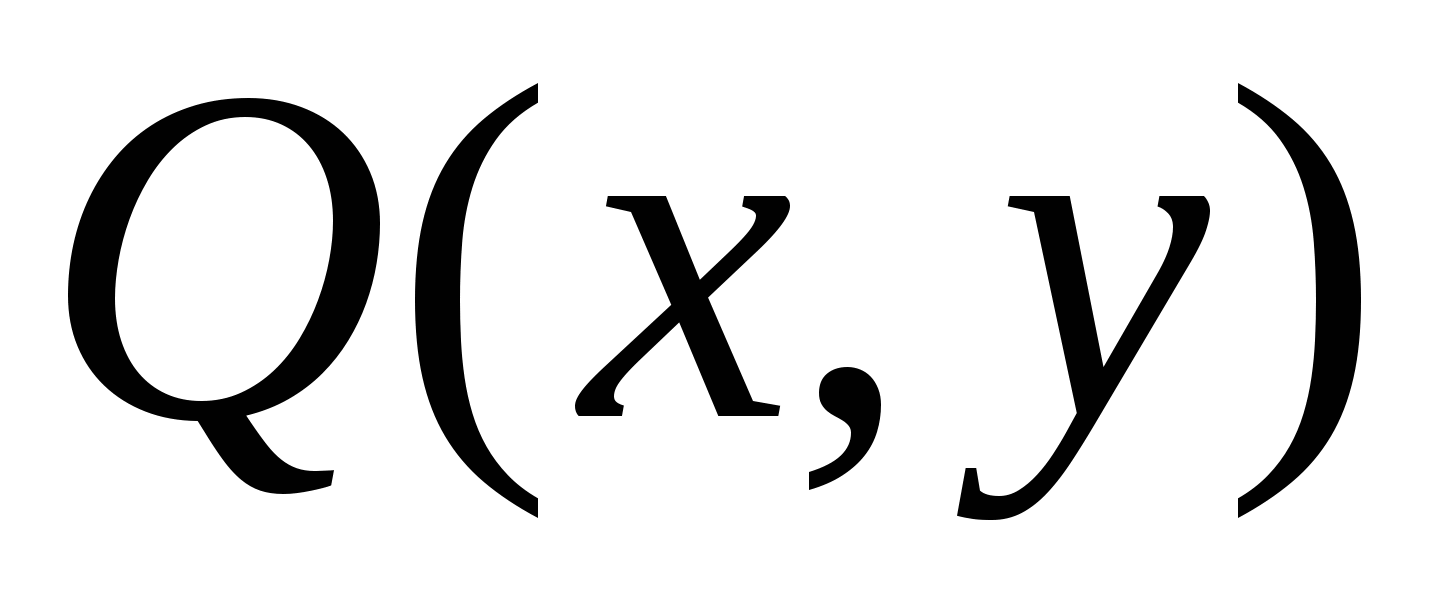 в области в области  , чтобы результат интегрирования по любой кривой, лежащей внутри , чтобы результат интегрирования по любой кривой, лежащей внутри  , и соединяющей две фиксированные точки, был одинаковым. , и соединяющей две фиксированные точки, был одинаковым.
Очевидно, что условие независимости результата интегрирования криволинейного интеграла по кривой, соединяющей две фиксированные точки области, от формы этой кривой равносильно условию равенства нулю интеграла по любой замкнутой кривой, лежащей в этой области. Действительно, обозначим через 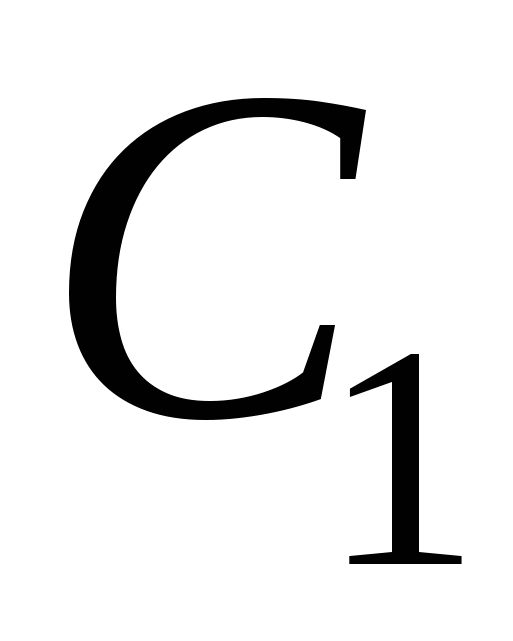 и и 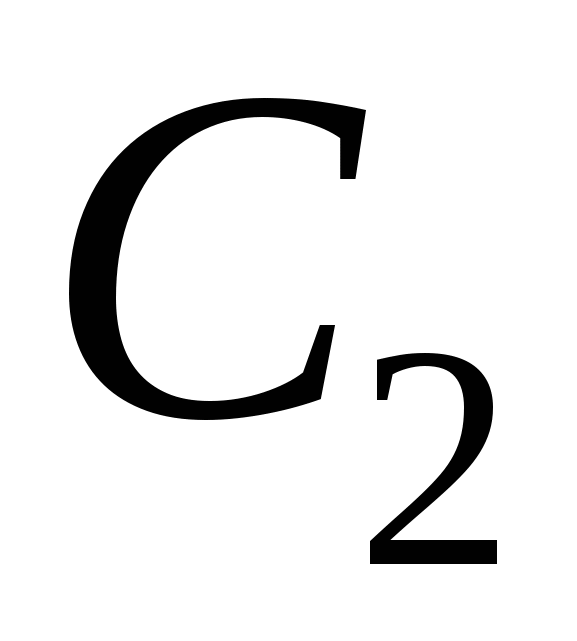 две кривые, лежащие в две кривые, лежащие в  , с общими начальной и конечной точками. Тогда кривая , с общими начальной и конечной точками. Тогда кривая 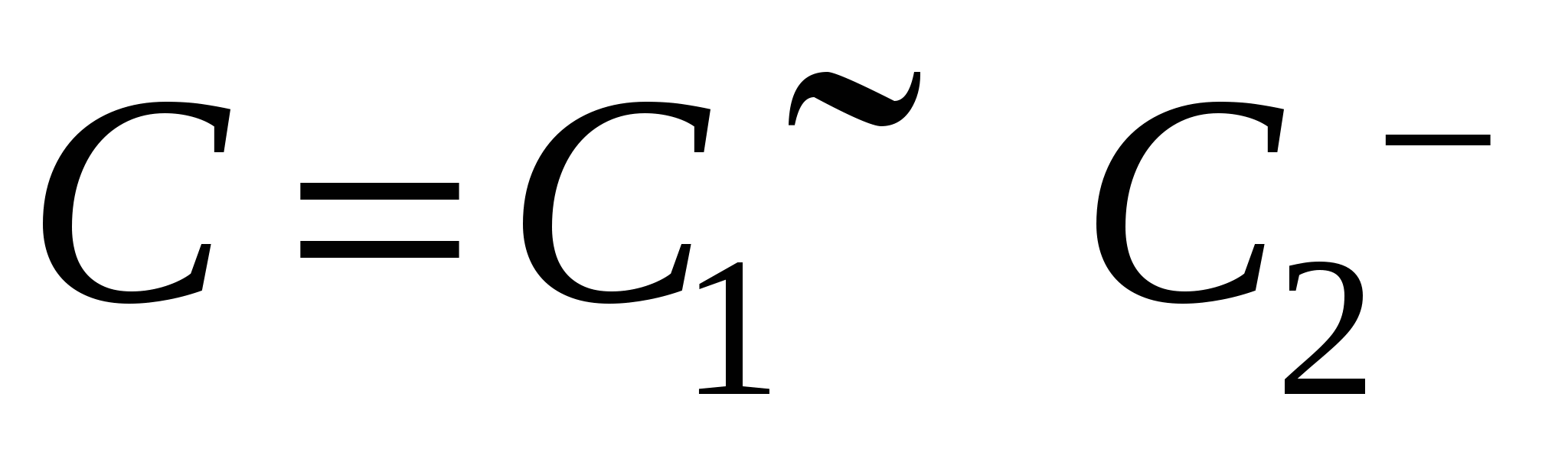 , где знак «-» означает, что соответствующая кривая проходится в противоположном направлении, будет замкнутой. Следовательно, соотношение , где знак «-» означает, что соответствующая кривая проходится в противоположном направлении, будет замкнутой. Следовательно, соотношение
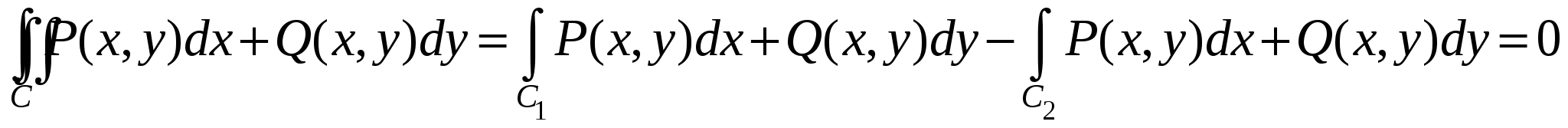
равносильно тому, что 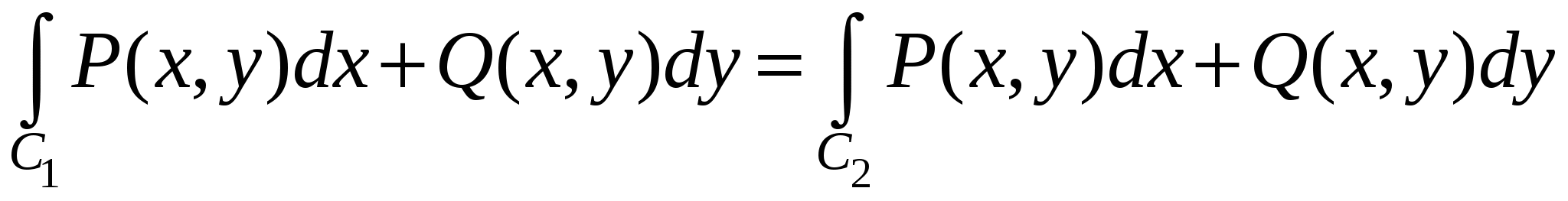 . .
Итак, найдем условие на функции 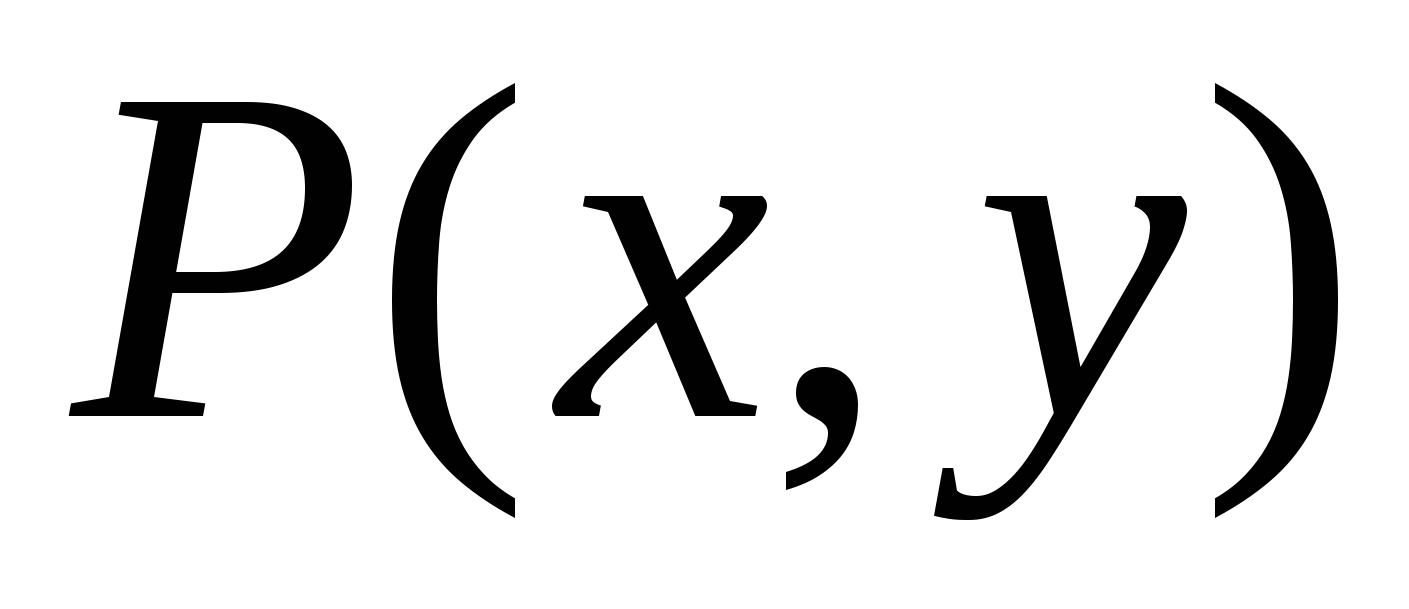 и и 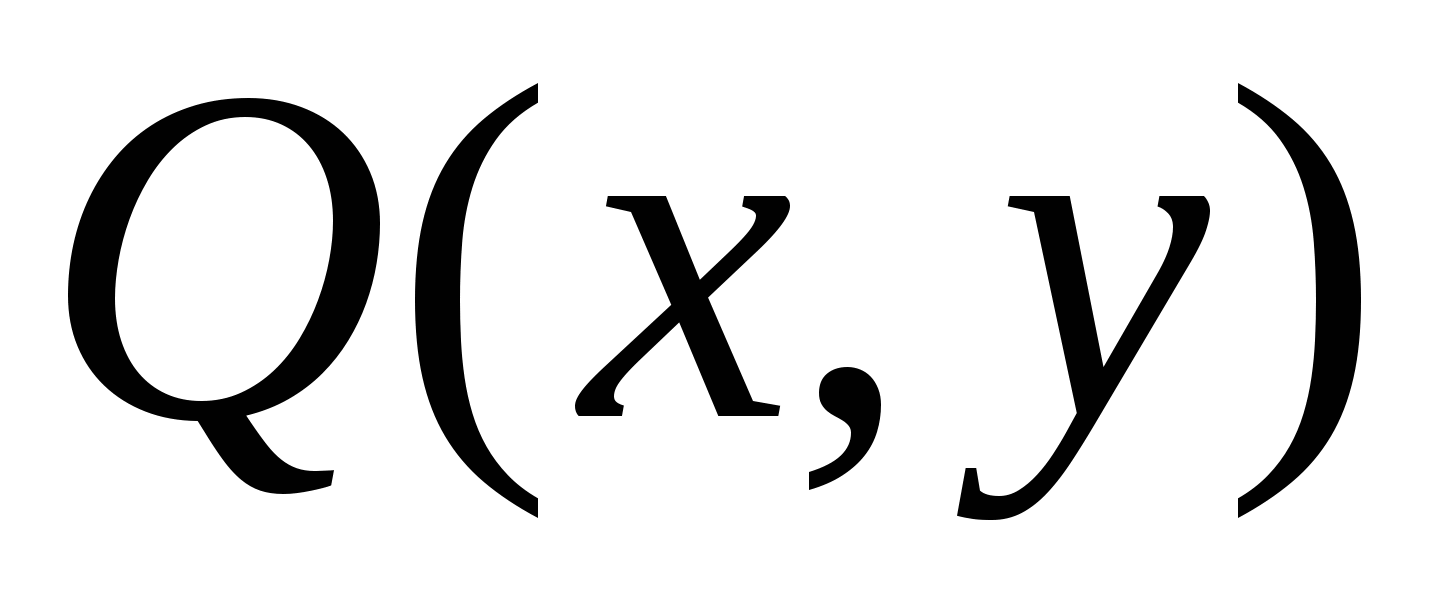 , необходимое и достаточное для того, чтобы криволинейный интеграл , необходимое и достаточное для того, чтобы криволинейный интеграл 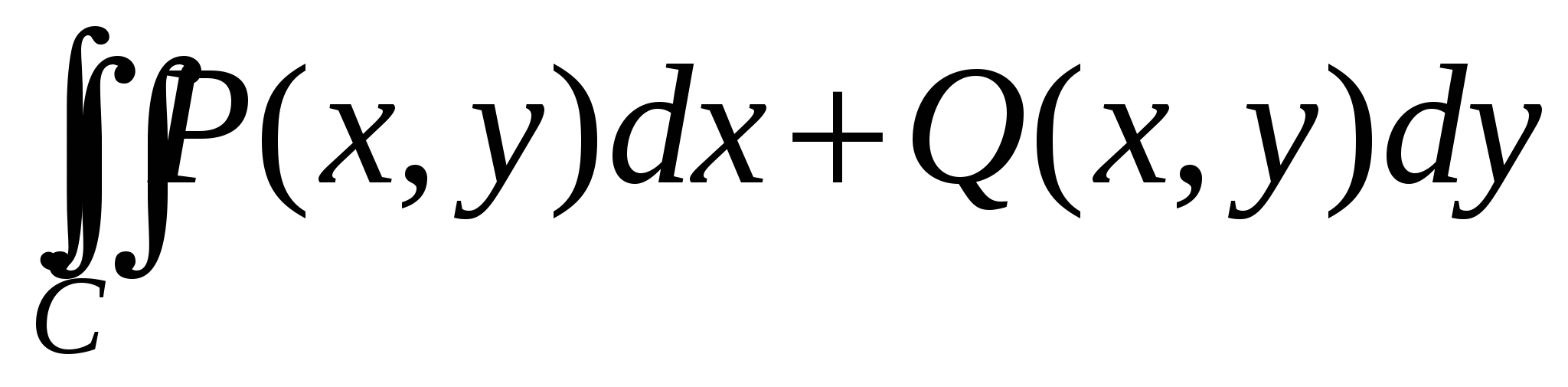 , где C – произвольная замкнутая кривая, лежащая в , где C – произвольная замкнутая кривая, лежащая в  , был равен нулю. , был равен нулю.
А. Докажем, что условие 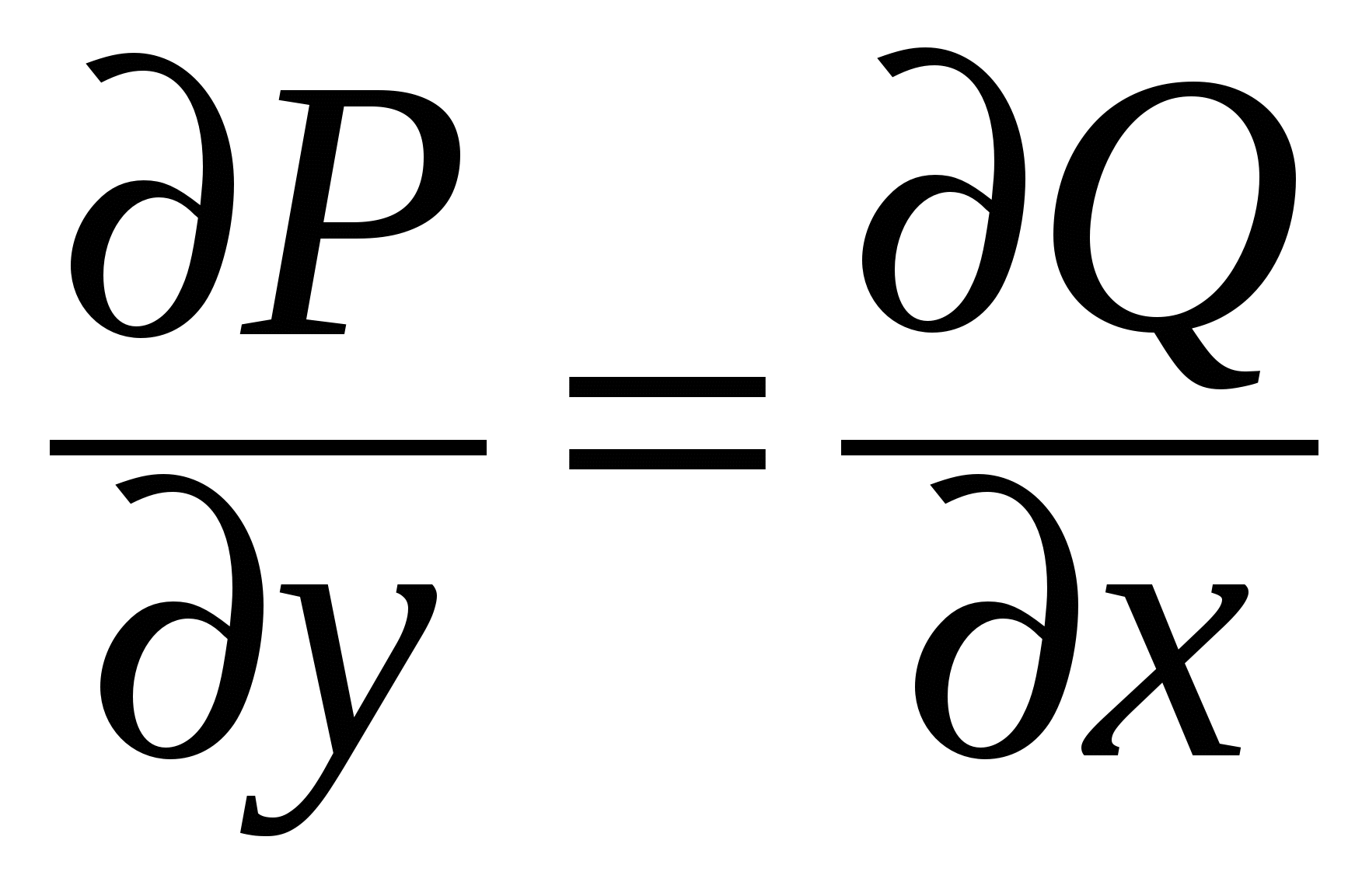 , выполняющееся всюду в , выполняющееся всюду в  для непрерывных функций для непрерывных функций 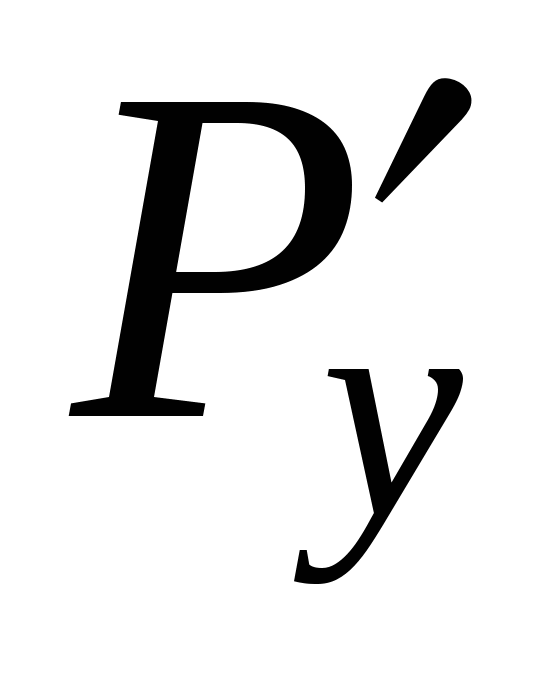 и и 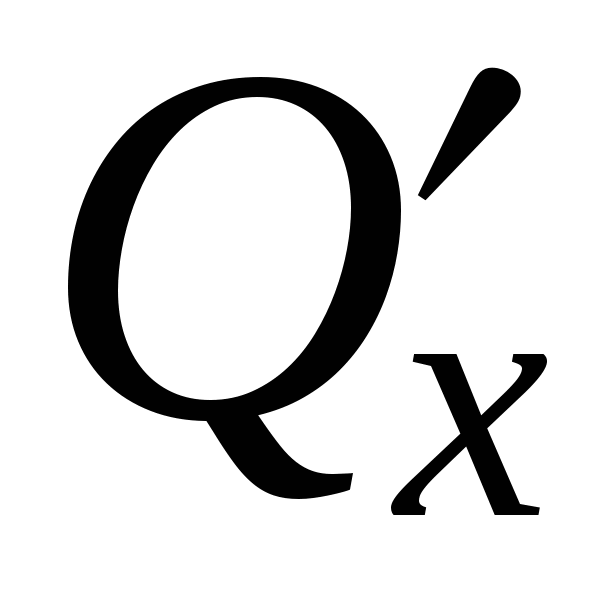 , является достаточным для того, чтобы криволинейный интеграл , является достаточным для того, чтобы криволинейный интеграл 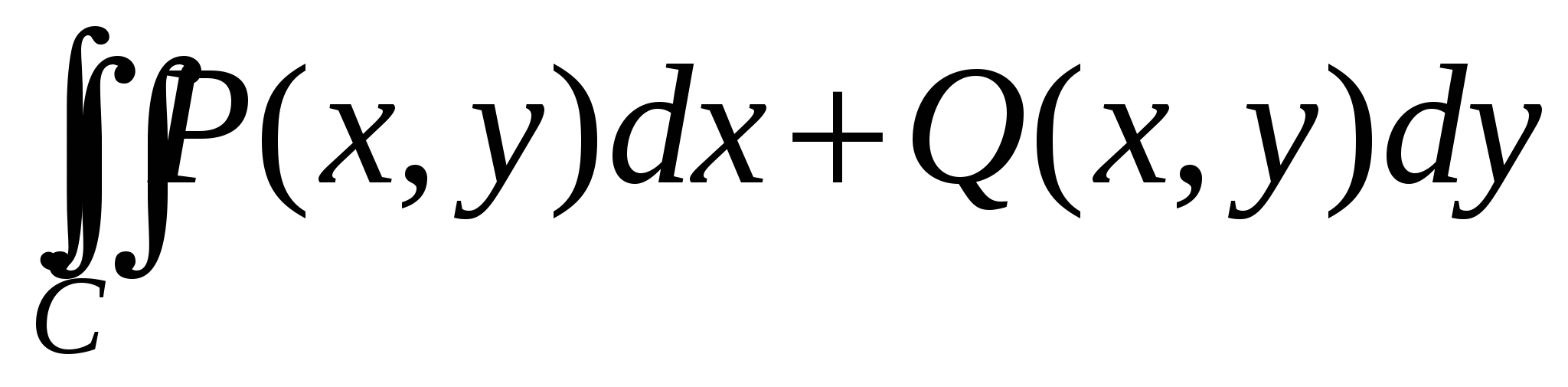 по любой замкнутой кривой C, лежащей в по любой замкнутой кривой C, лежащей в  , был нулем. Пусть C – замкнутая кривая без самопересечений. Тогда применим к интегралу , был нулем. Пусть C – замкнутая кривая без самопересечений. Тогда применим к интегралу 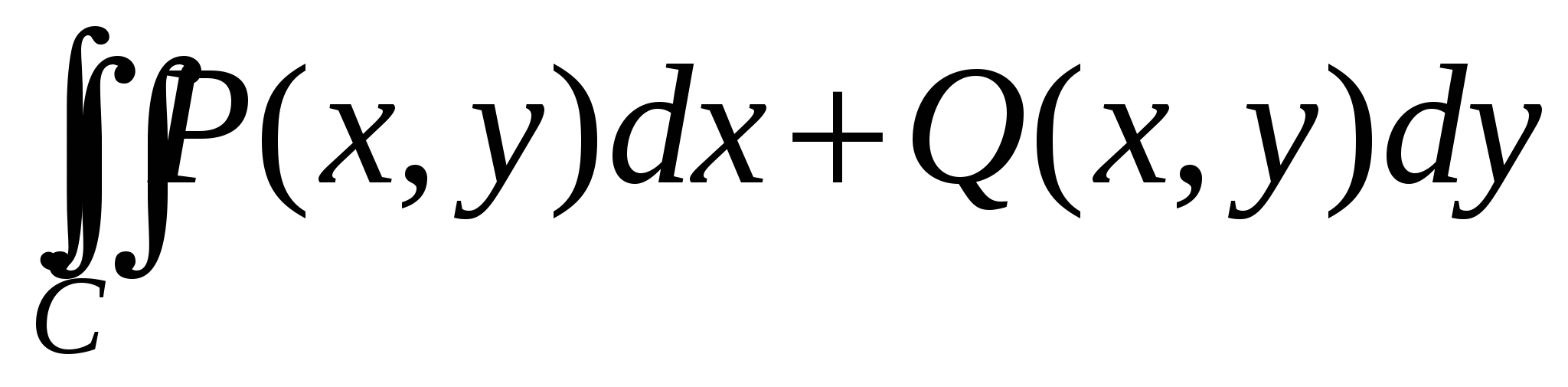 формулу Грина и с использованием условия формулу Грина и с использованием условия 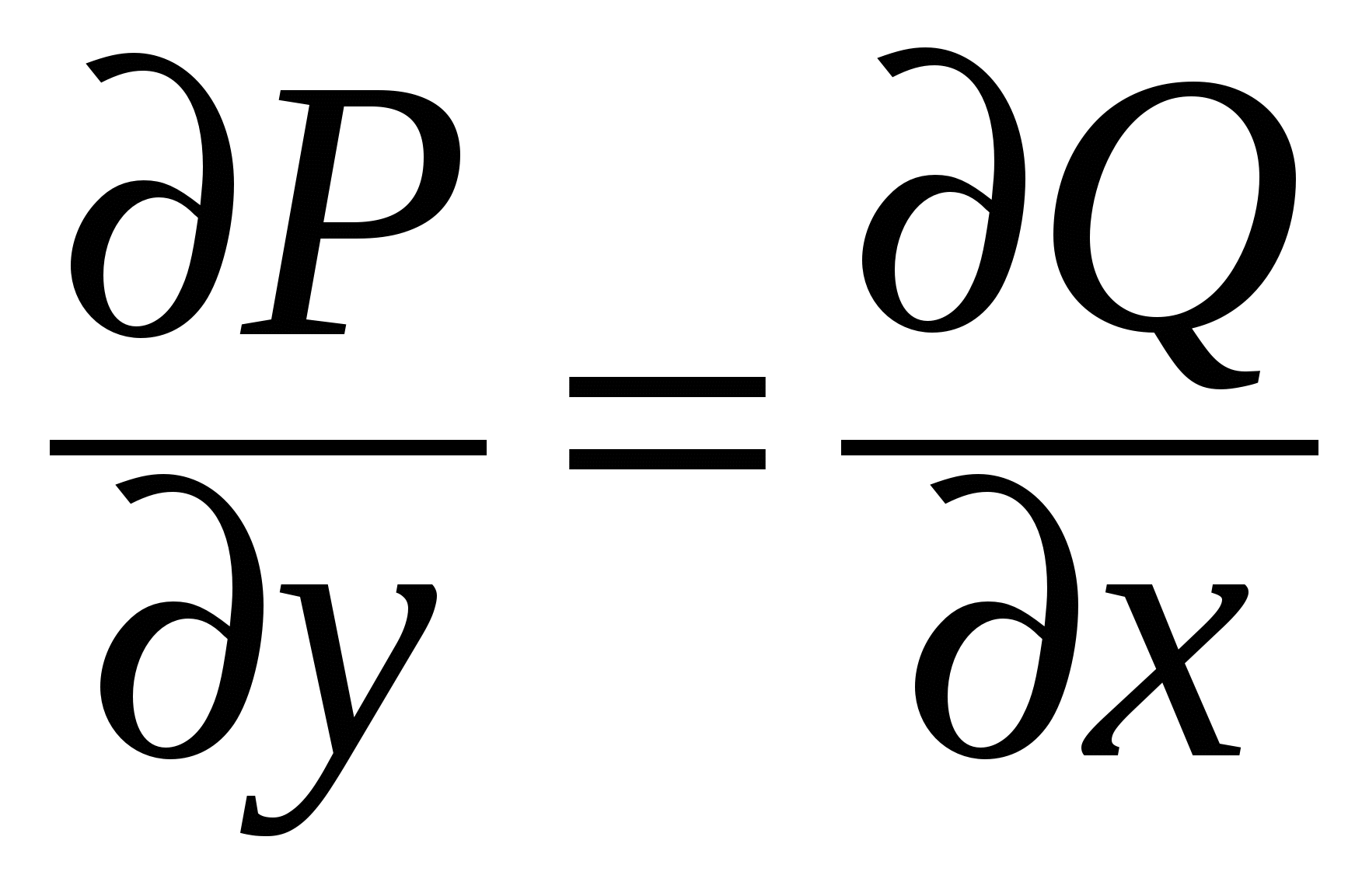 получим получим 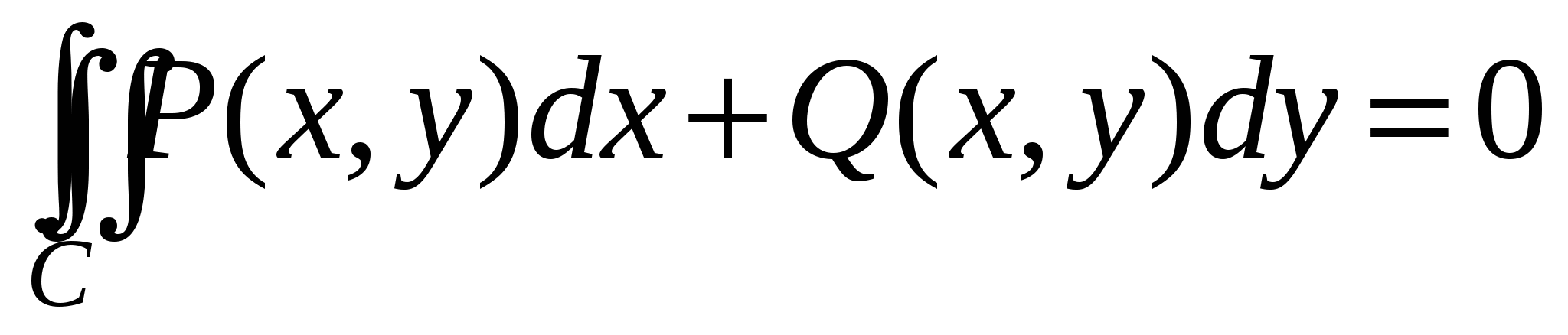 . .
Пусть теперь C – самопересекающаяся кривая, Тогда, как показано на рисунке, кривая C разбивается точками самопересечения на конечное число фрагментов, которые

попарно соединяются в объединение нескольких замкнутых кривых без самопересечений. Применяя к интегралу по этим кривым формулу Грина, мы так же, как и выше, получим 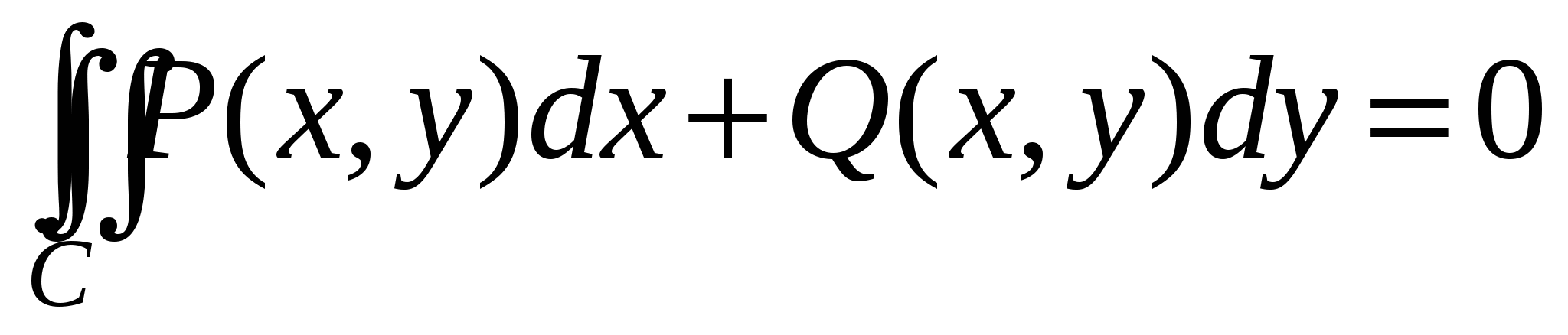 . .
Б. Докажем, что выполнение условия 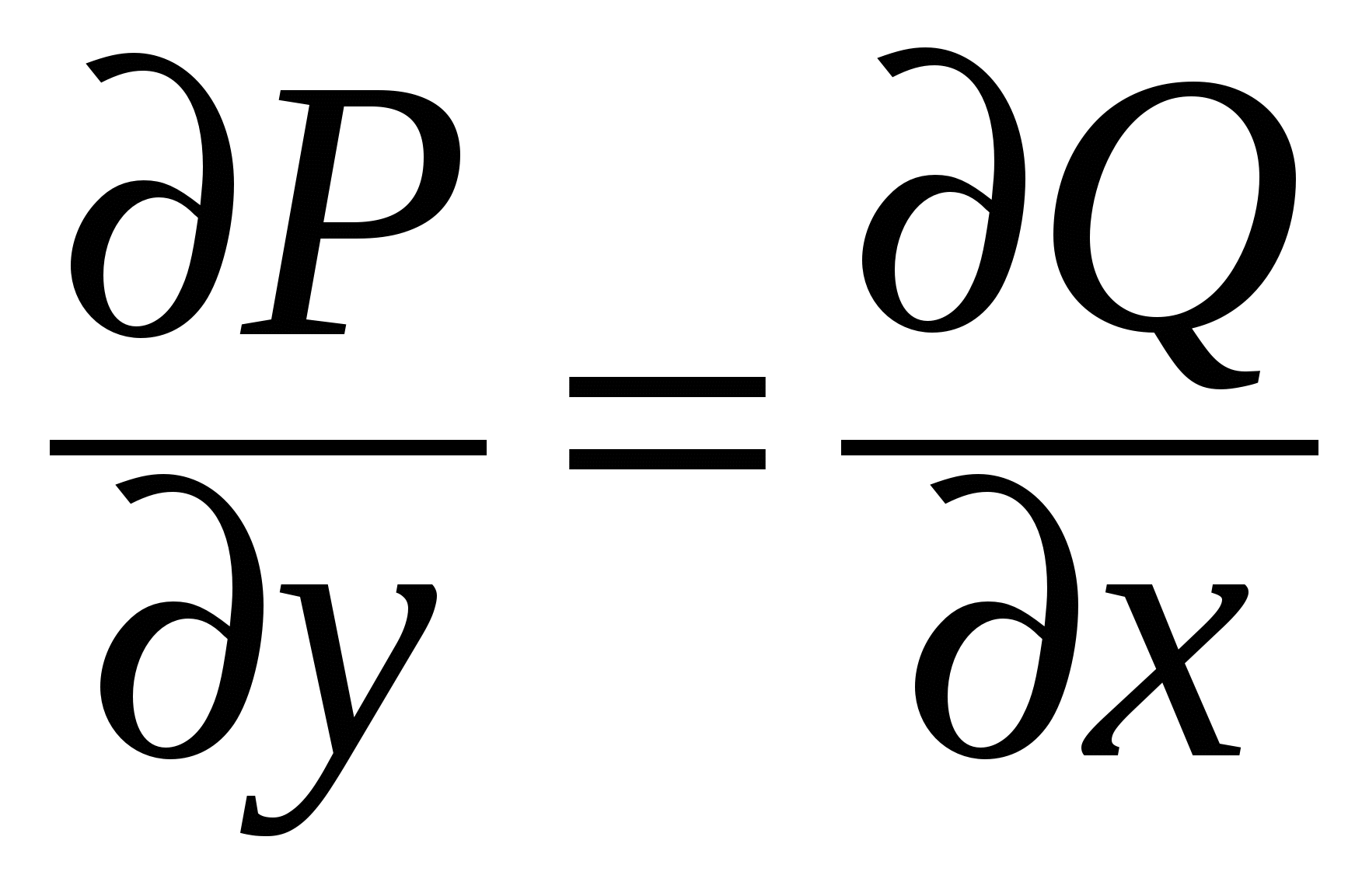 в в  для непрерывных функций для непрерывных функций  и и  , является необходимым условием того, что , является необходимым условием того, что 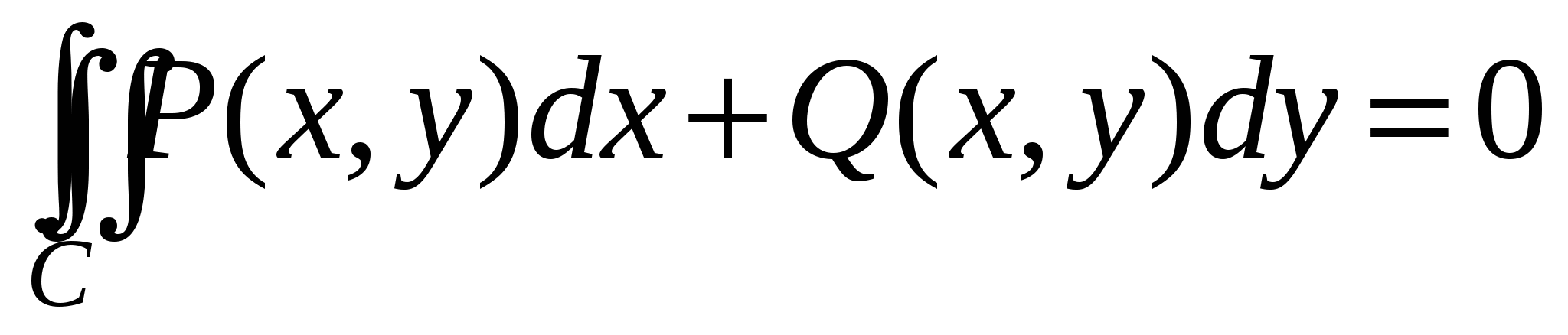 для любой замкнутой лежащей в для любой замкнутой лежащей в  кривой C. Предположим противное: пусть интеграл по любой замкнутой кривой равен нулю, но кривой C. Предположим противное: пусть интеграл по любой замкнутой кривой равен нулю, но 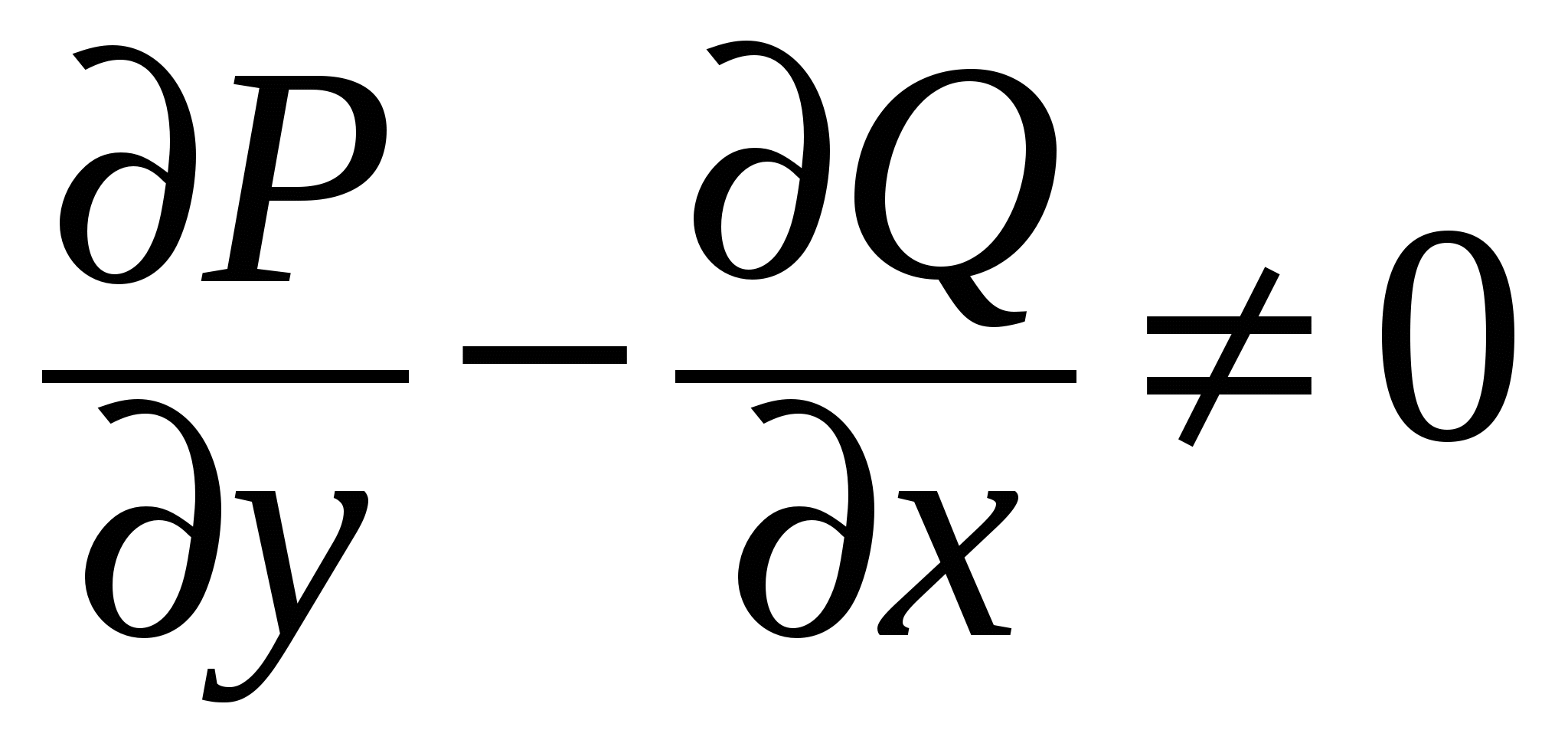 в некоторой внутренней точке M области в некоторой внутренней точке M области  . Допустим, . Допустим, 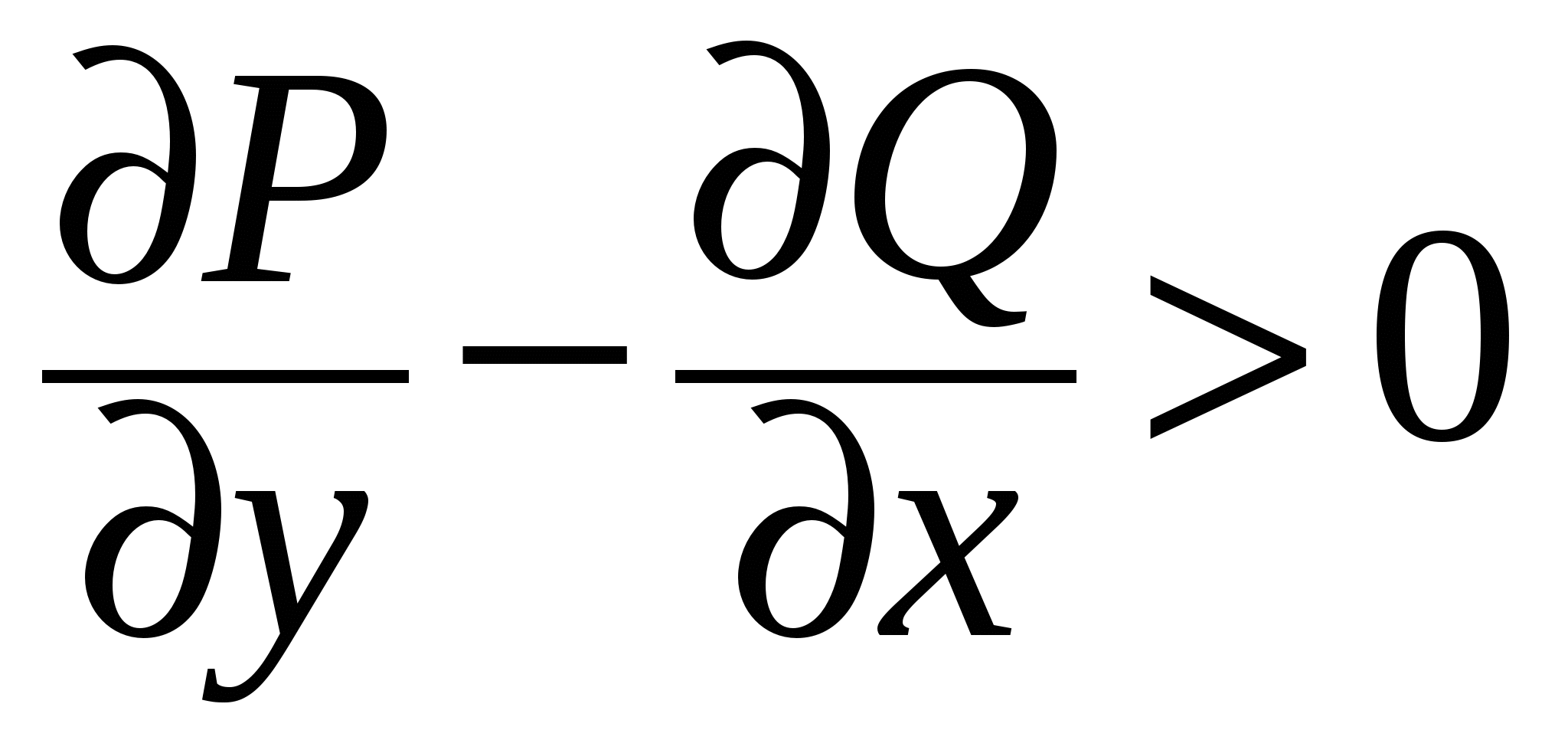 в этой точке. В силу непрерывности в этой точке. В силу непрерывности 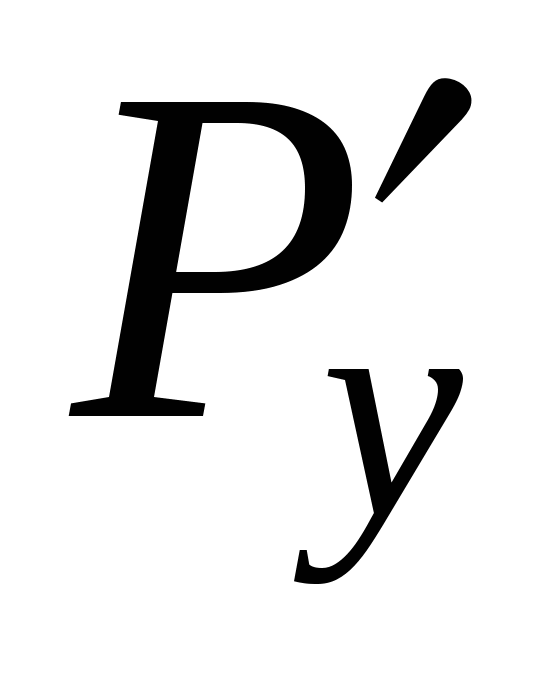 и и 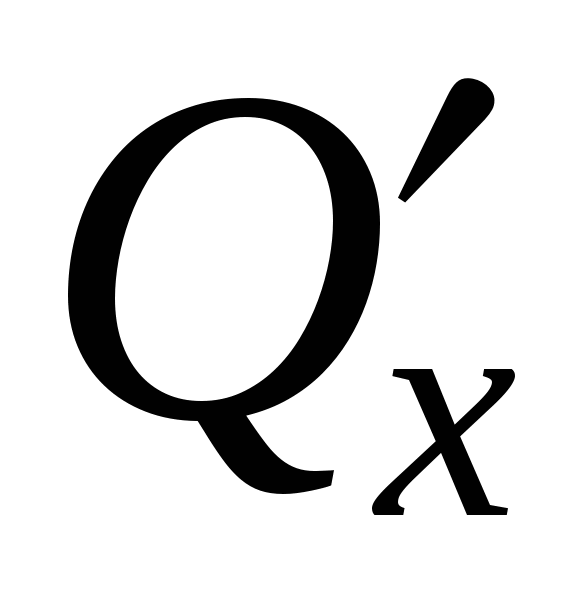 существует окрестность точки M, лежащая в существует окрестность точки M, лежащая в  , в которой также , в которой также 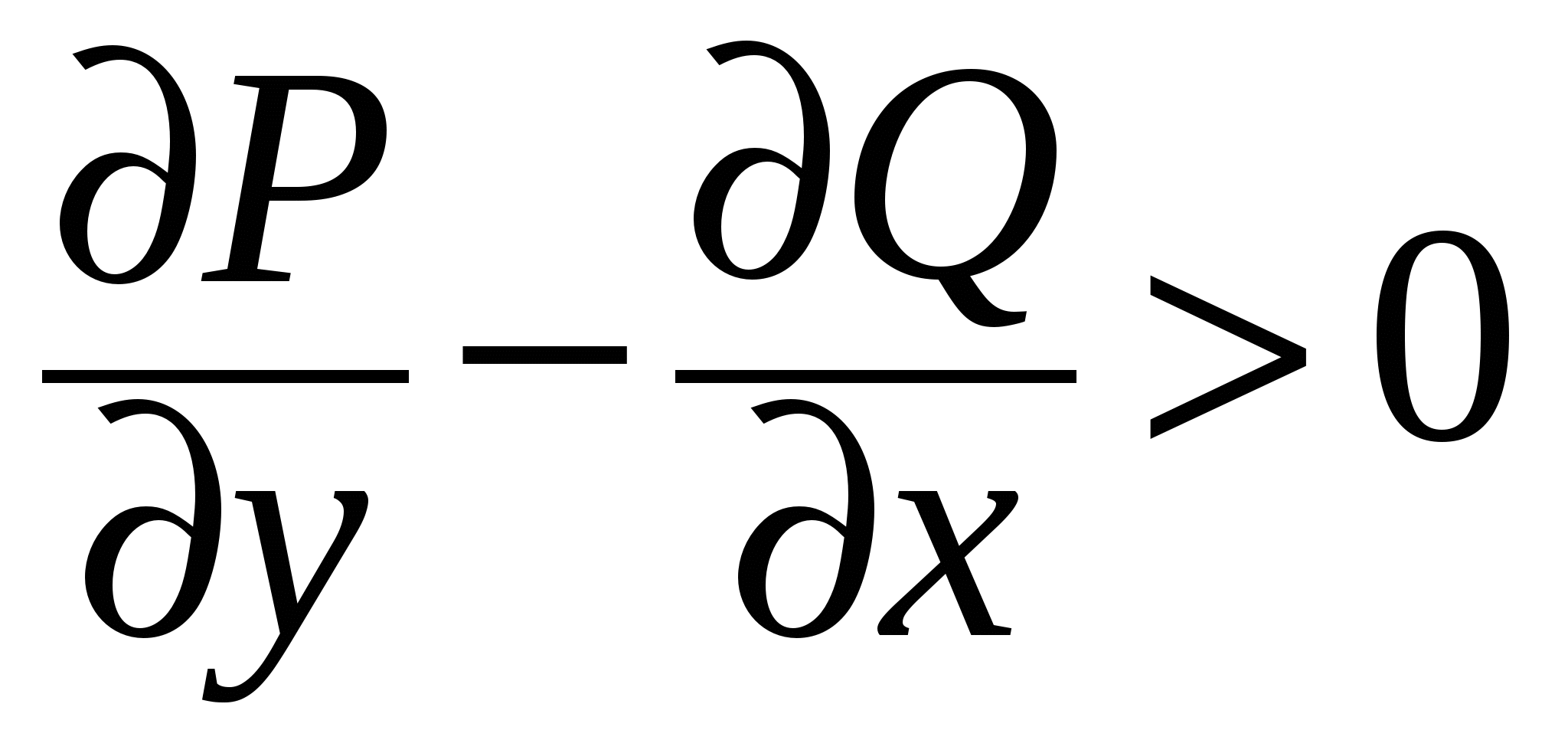 . Возьмем область D в этой окрестности с границей C. Согласно формуле Грина, примененной к кривой C и области D, . Возьмем область D в этой окрестности с границей C. Согласно формуле Грина, примененной к кривой C и области D, 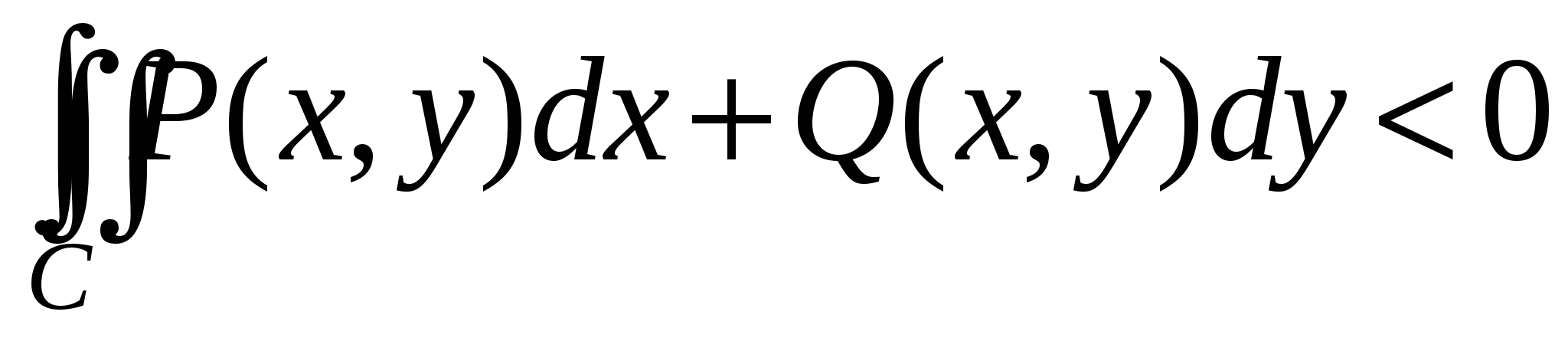 , что противоречит предположению о том, что интеграл по любой замкнутой кривой в , что противоречит предположению о том, что интеграл по любой замкнутой кривой в  равен нулю. Противоречие доказывает необходимость выполнения условия равен нулю. Противоречие доказывает необходимость выполнения условия 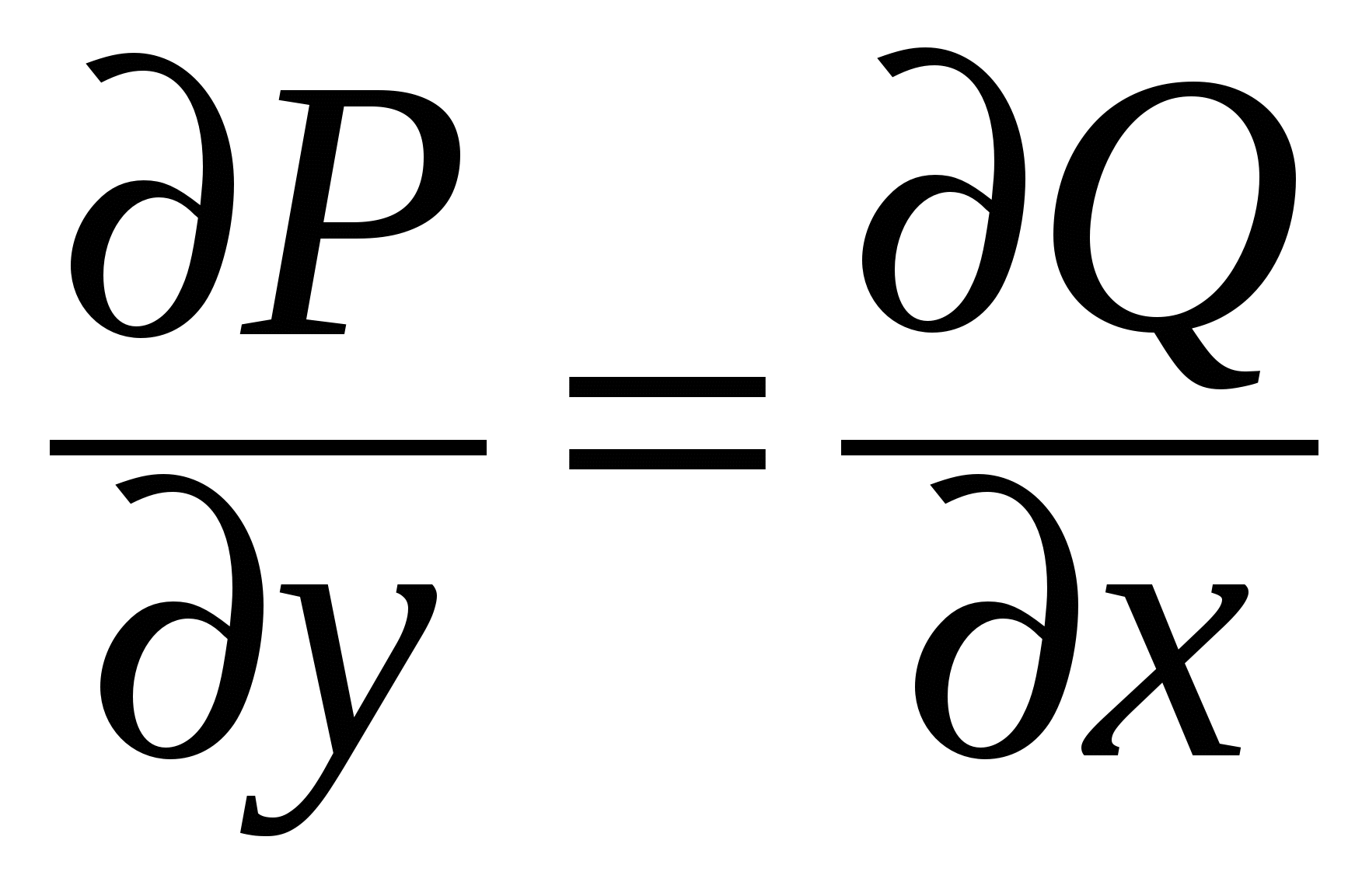 всюду в всюду в  . .
Поверхностные интегралы
Поверхностный интеграл первого рода.
В теории поверхностных интегралов большую роль играет понятие площади поверхности. Определение площади поверхности как предела суммы площадей фрагментов касательных к поверхности плоскостей было введено в разделе «Двойной интеграл». Там же приведены формулы для вычисления площадей поверхностей, заданных явно и параметрически.
Задача о вычислении массы неоднородной оболочки.
Пусть S – поверхность в пространстве XYZ. Тяжелая неоднородная оболочка расположена в пространстве в виде этой поверхности. Плотность оболочки, рассчитанная на единицу площади поверхности, зависит от местоположения точки на поверхности и равна 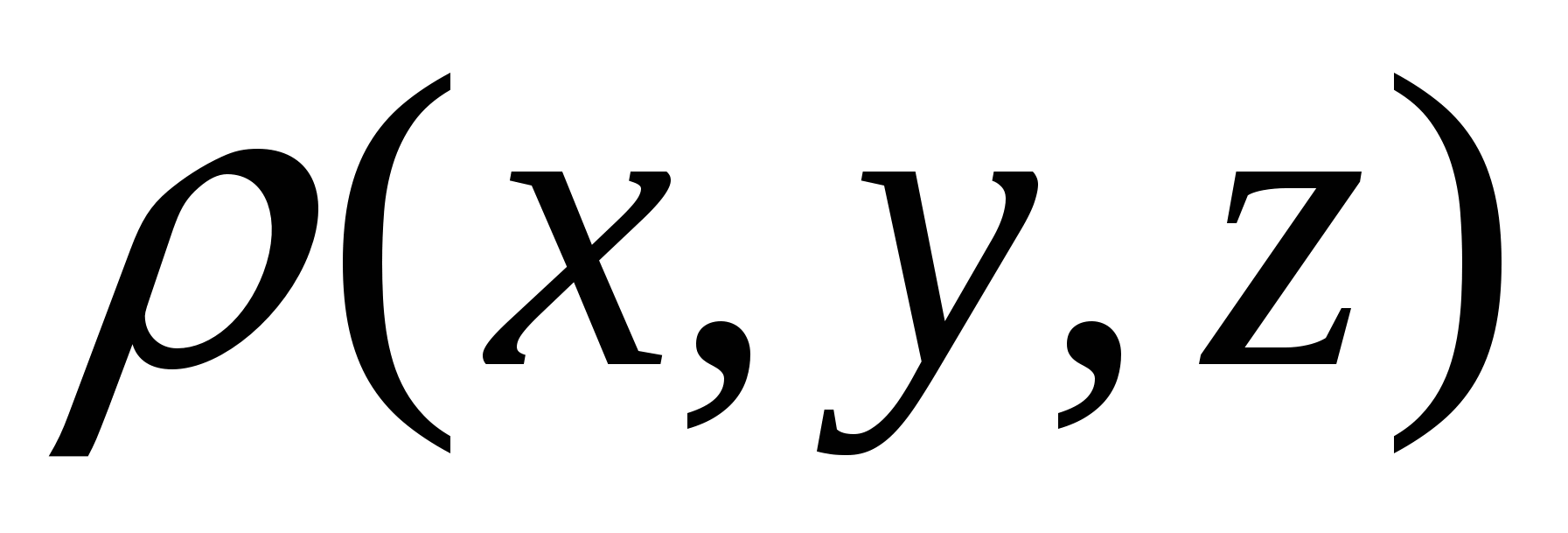 , причем , причем 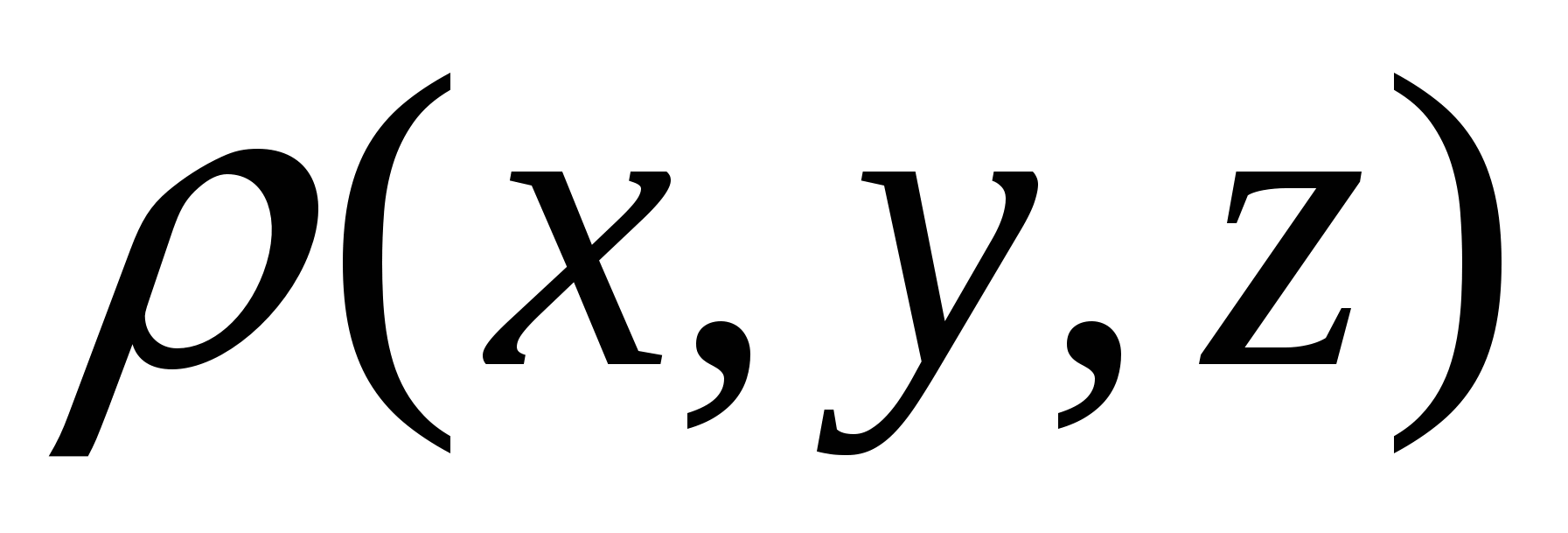 – непрерывная на S функция. Для того, чтобы вычислить массу неоднородной оболочки, разобьем поверхность S на n фрагментов – непрерывная на S функция. Для того, чтобы вычислить массу неоднородной оболочки, разобьем поверхность S на n фрагментов 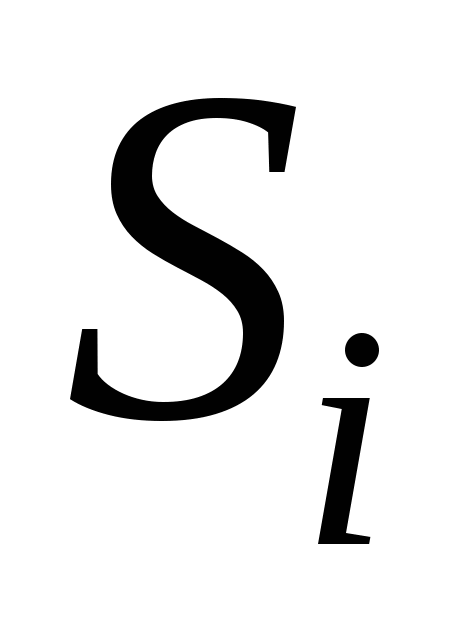 с площадями с площадями 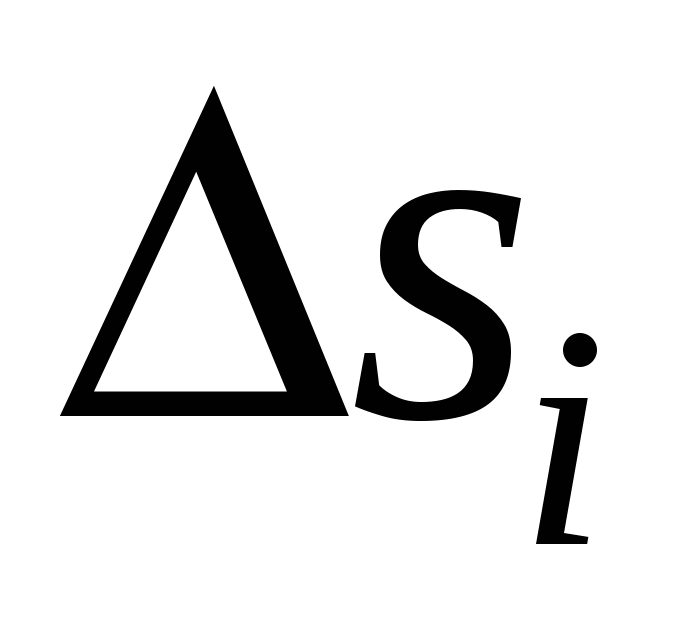 и на каждом таком фрагменте и на каждом таком фрагменте 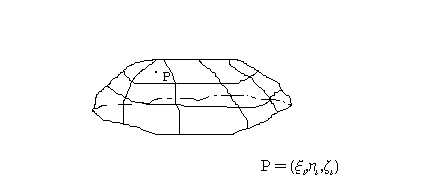
выберем точку 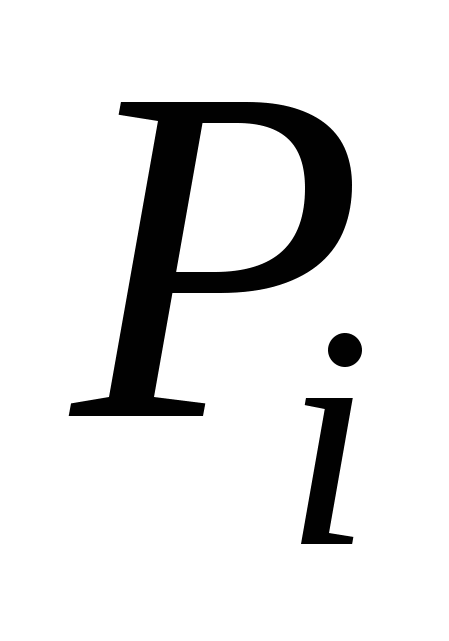 с координатами с координатами 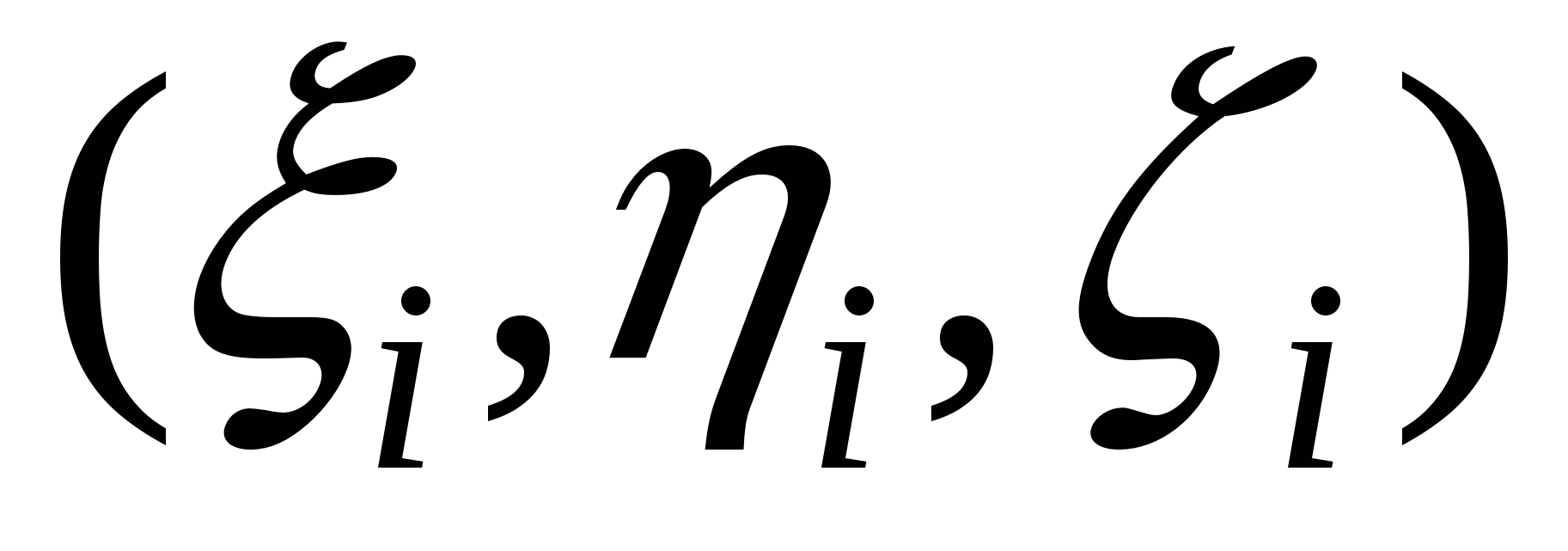 . Найдем значение . Найдем значение 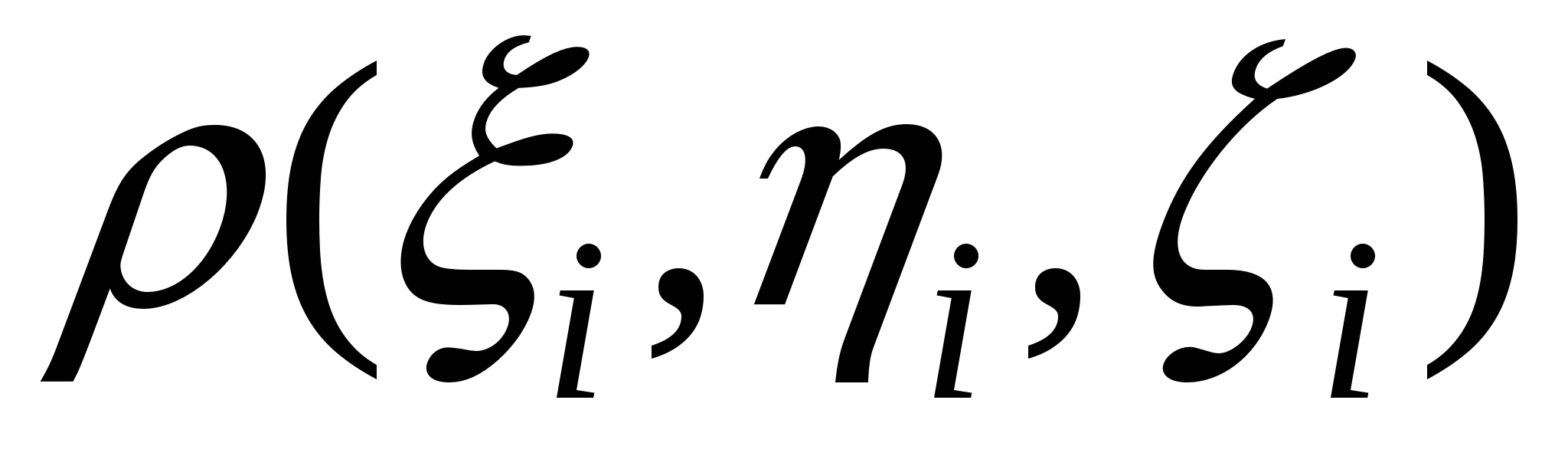 . Предполагая, что площадь i-го поверхностного фрагмента мала и учитывая, что плотность непрерывна, получим, что масса этого фрагмента будет приблизительно равна . Предполагая, что площадь i-го поверхностного фрагмента мала и учитывая, что плотность непрерывна, получим, что масса этого фрагмента будет приблизительно равна 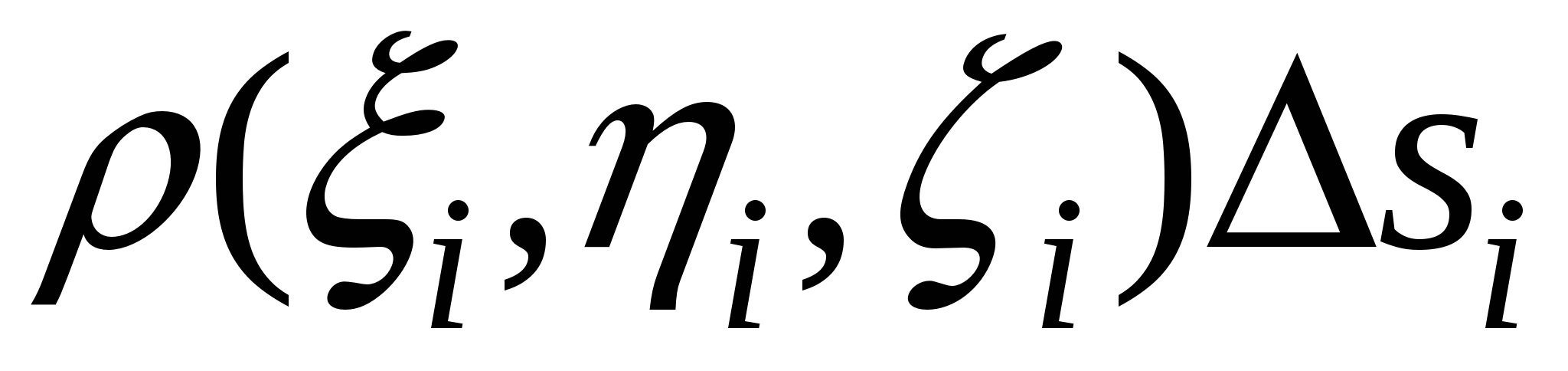 , причем чем меньше фрагмент, тем точнее полученная масса этого фрагмента. Поэтому массу всей оболочки можно получить, просуммировав массы всех фрагментов и устремив к нулю площади фрагментов, одновременно увеличивая количество фрагментов, на которые разбита поверхность. Таким образом, выражение для массы оболочки будет иметь вид , причем чем меньше фрагмент, тем точнее полученная масса этого фрагмента. Поэтому массу всей оболочки можно получить, просуммировав массы всех фрагментов и устремив к нулю площади фрагментов, одновременно увеличивая количество фрагментов, на которые разбита поверхность. Таким образом, выражение для массы оболочки будет иметь вид
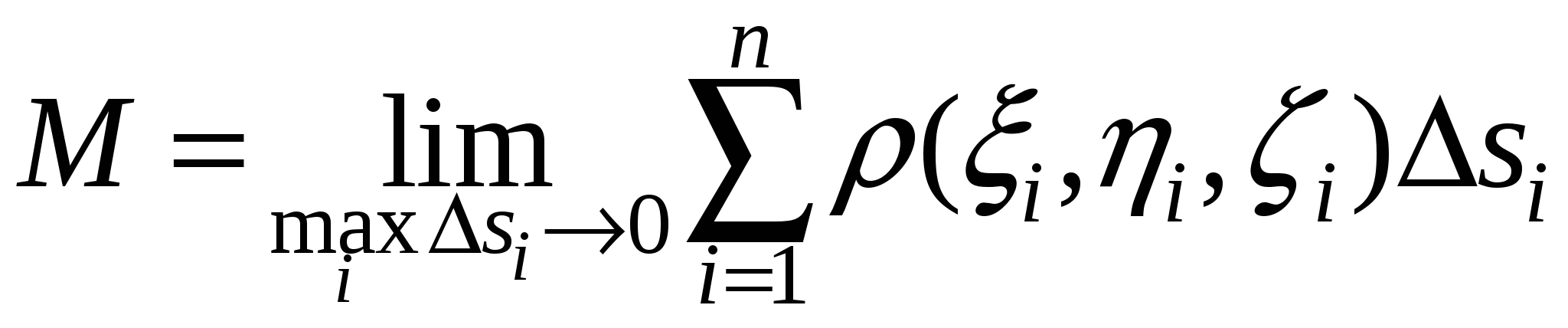 . .
Представим предел интегральной суммы через двойной интеграл, так как сомножитель 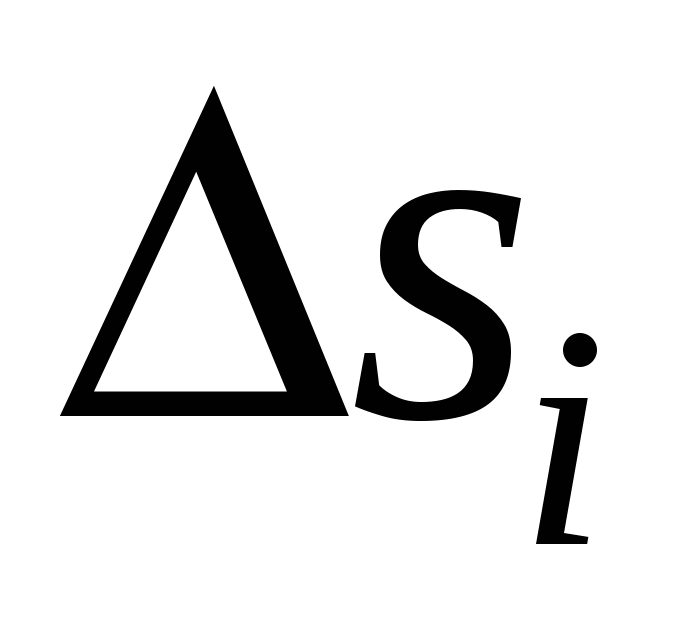 – элемент площади. В результате предельного перехода получим – элемент площади. В результате предельного перехода получим 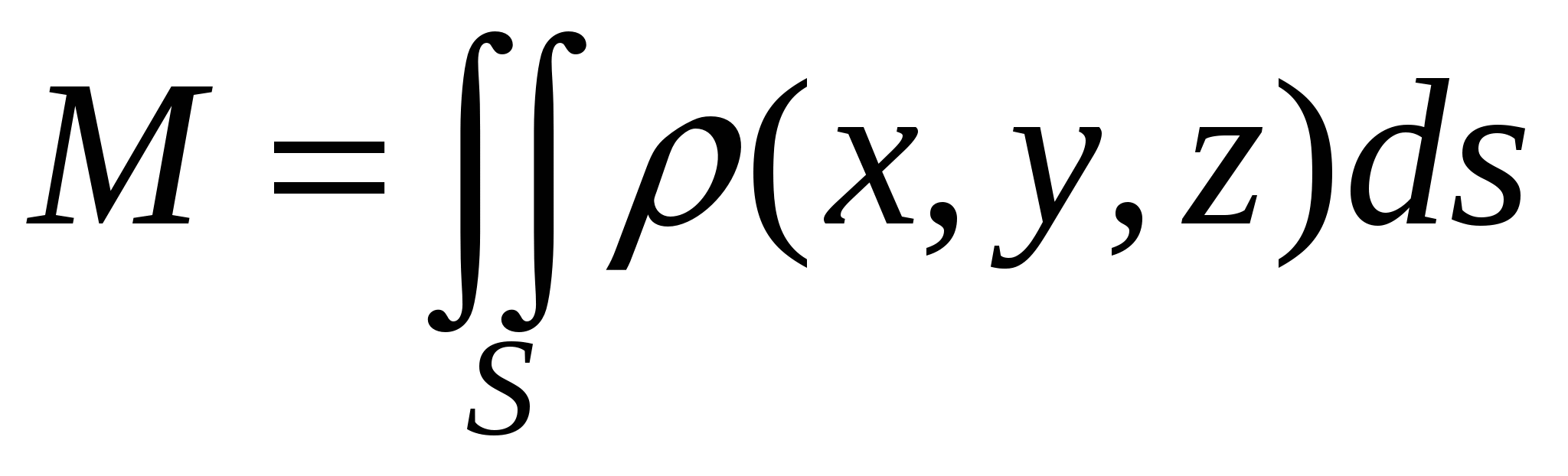 . .
Интеграл, стоящий в правой части последнего выражения, называется поверхностным интегралом первого рода или поверхностным интегралом по площади поверхности. Заметим, что результат интегрирования не зависит от выбора стороны оболочки.
С помощью поверхностного интеграла 1-го рода можно вычислять не только массу оболочки, но и другие физические характеристики оболочки: моменты, центр тяжести.
Способ вычисления поверхностного интеграла первого рода.
Пусть требуется вычислить 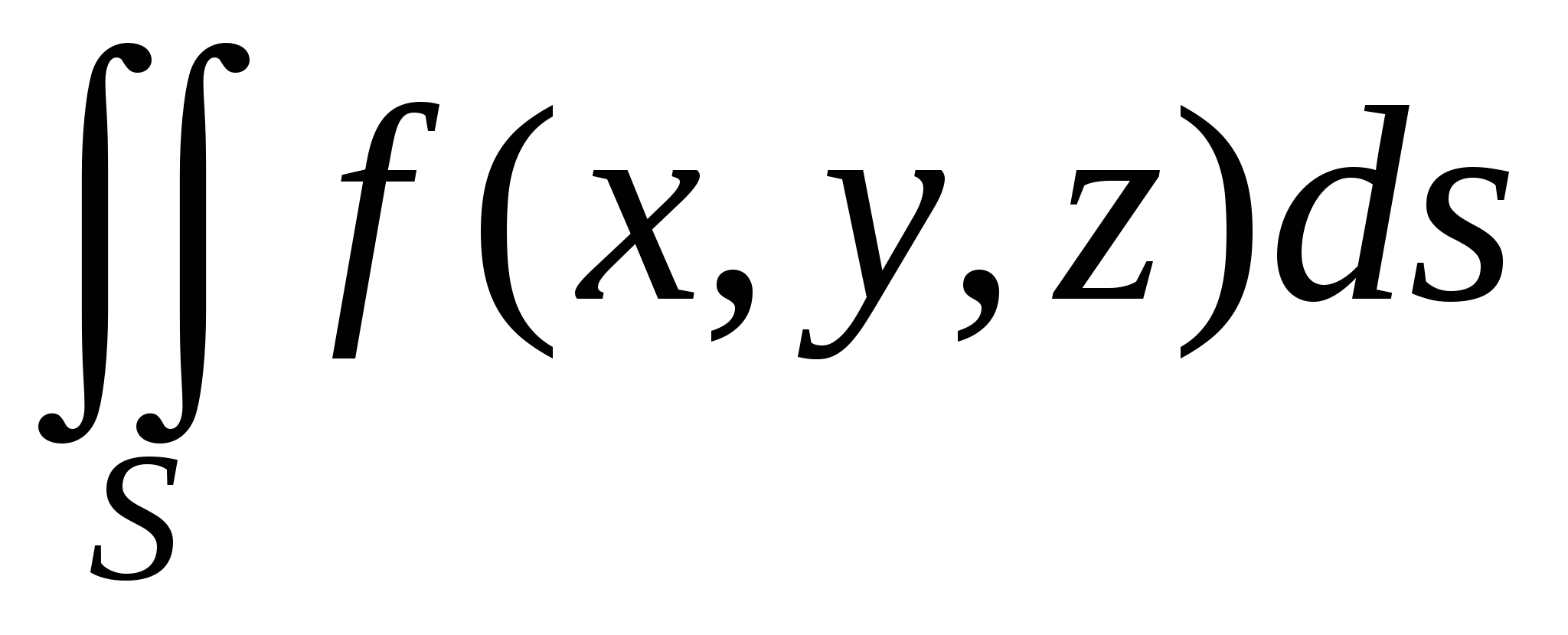 , когда функция , когда функция 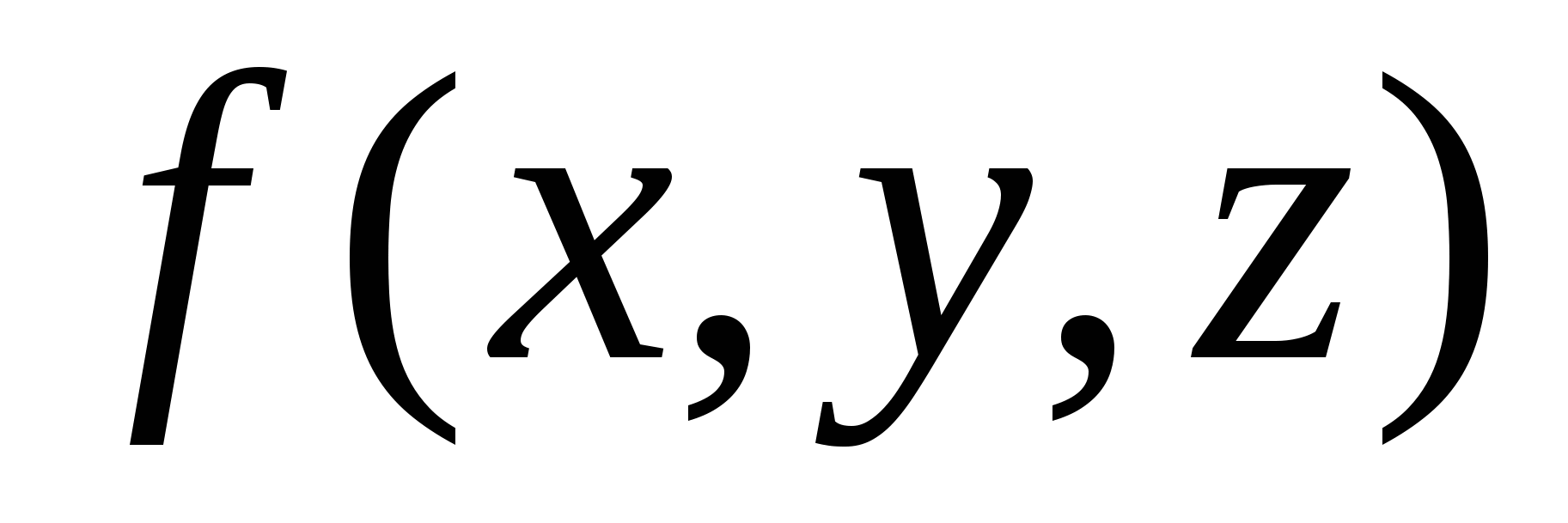 непрерывна на поверхности S. Поверхность S задана параметрически: непрерывна на поверхности S. Поверхность S задана параметрически: 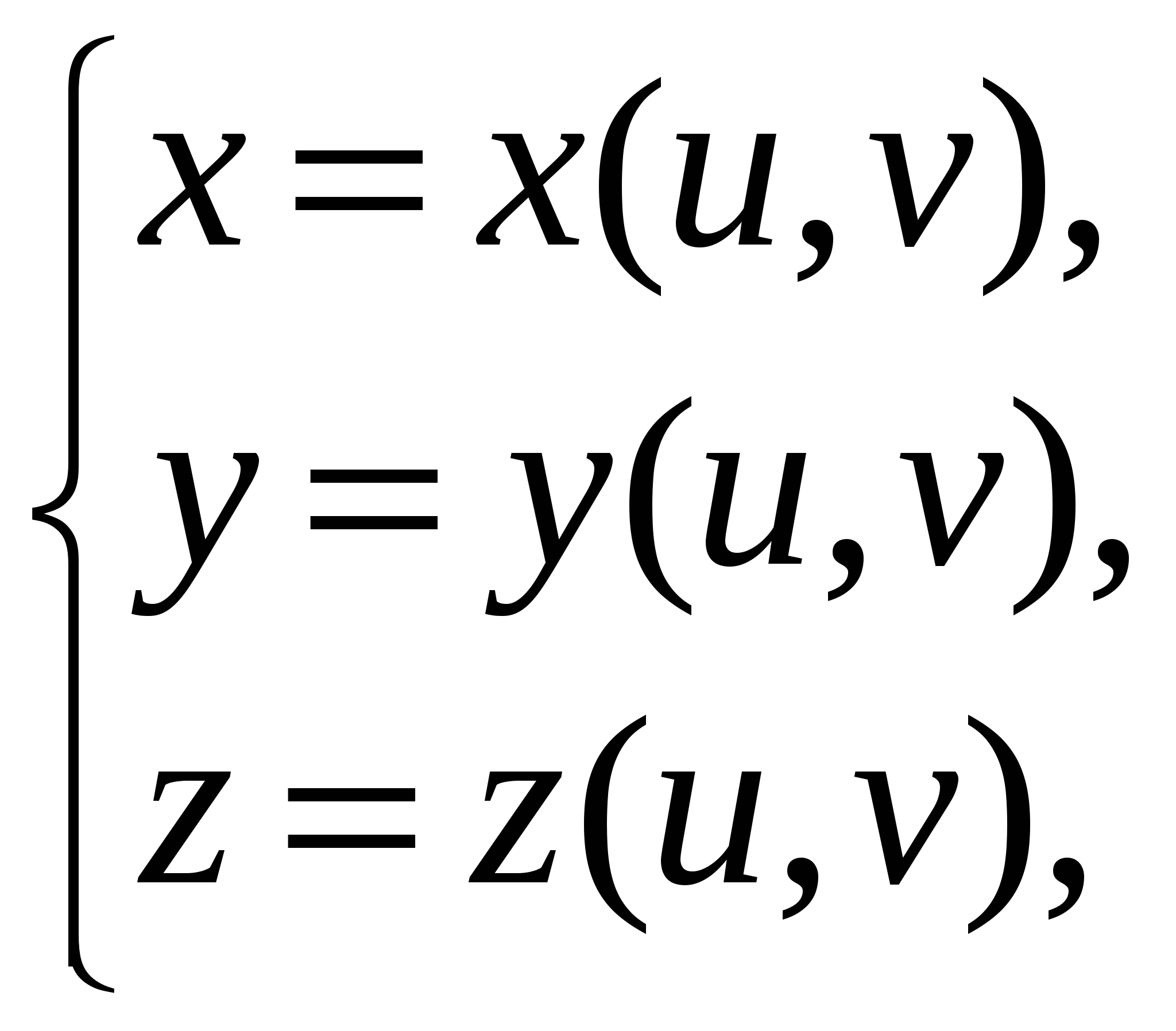 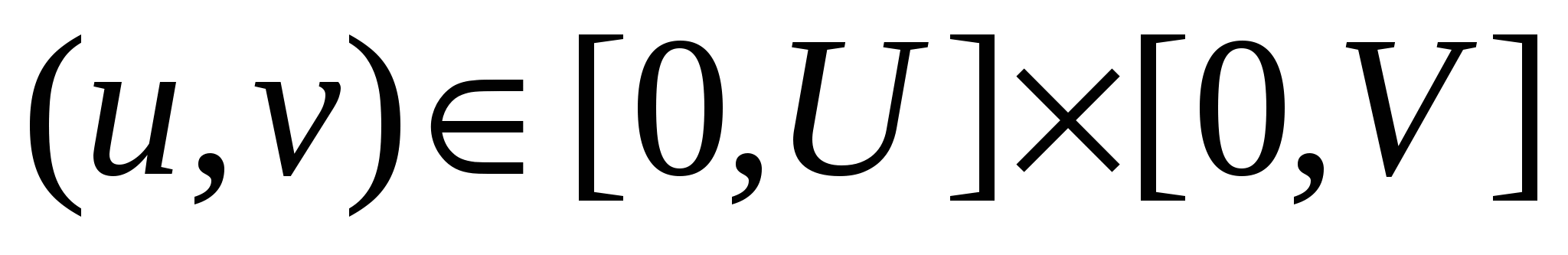 , где функции , где функции 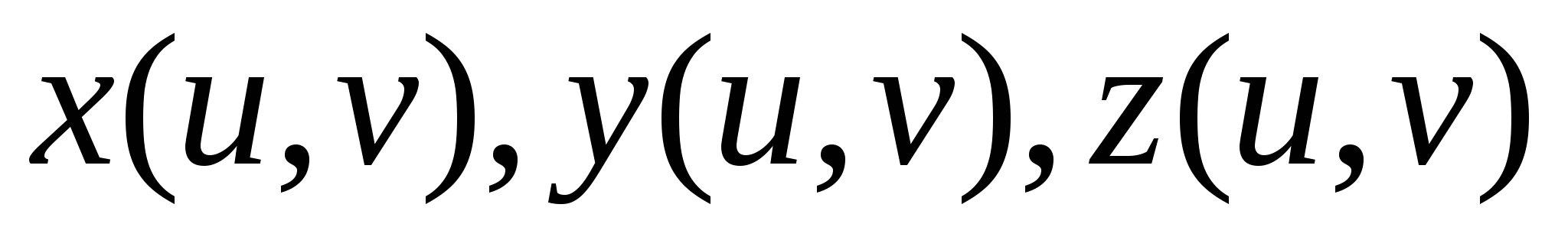 имеют непрерывные в прямоугольнике имеют непрерывные в прямоугольнике 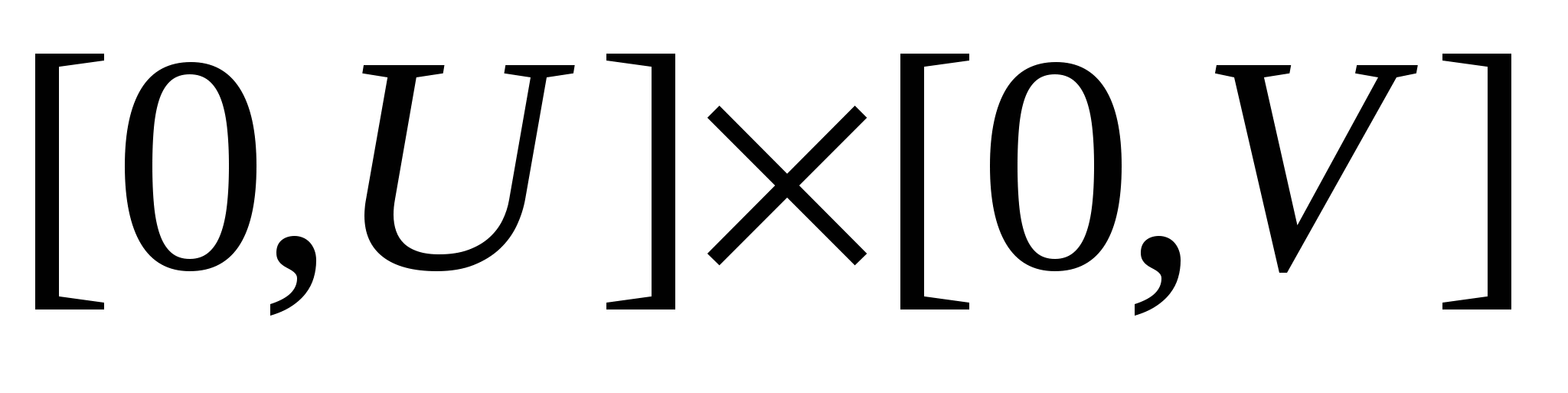 частные производные первого порядка. Разобьем прямоугольник значений параметров частные производные первого порядка. Разобьем прямоугольник значений параметров 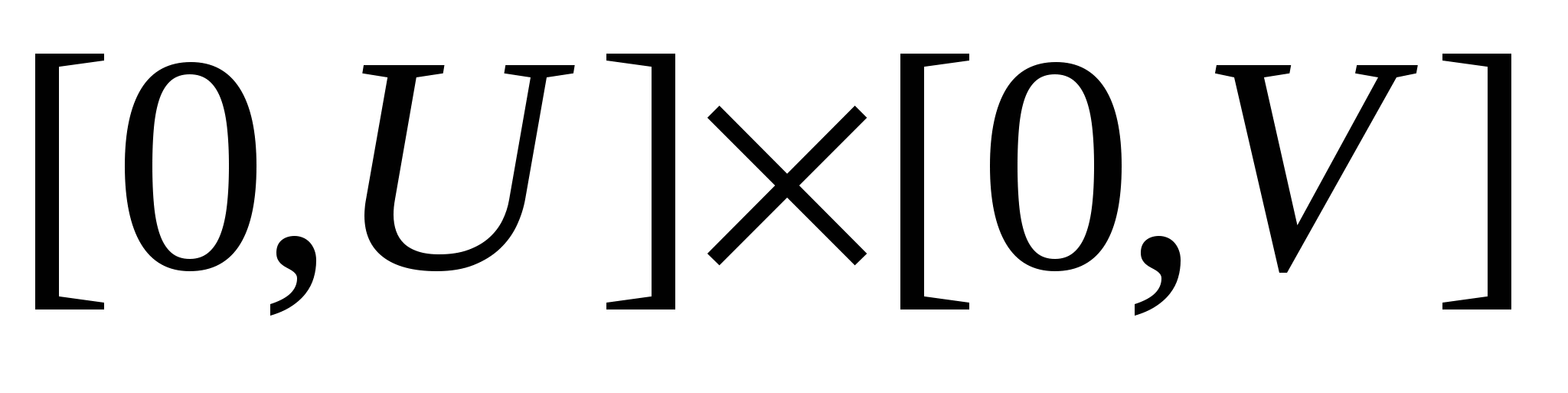 на прямоугольники на прямоугольники 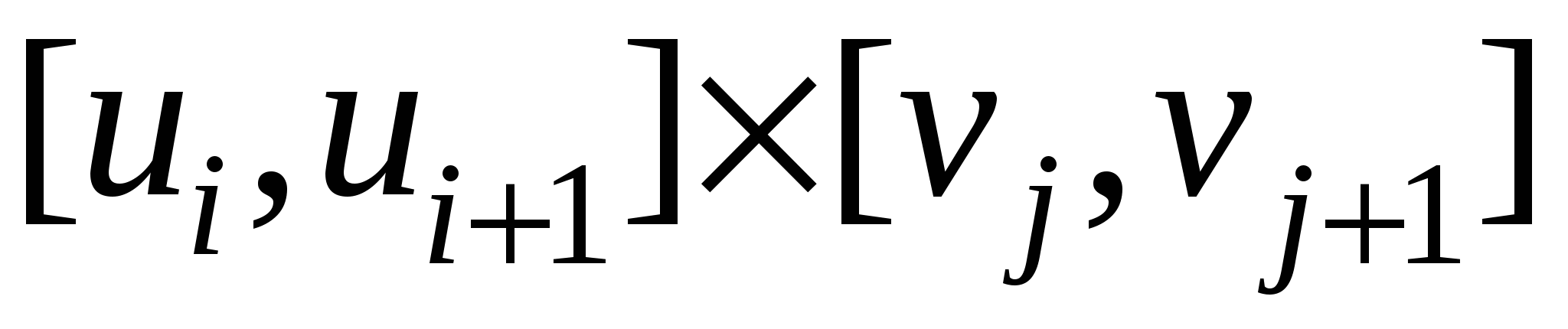 , , 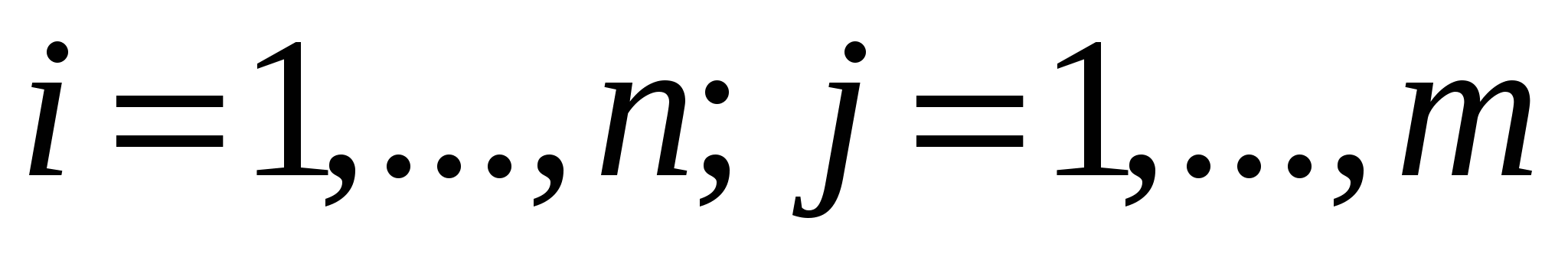 . Соответственно такому разбиению прямоугольника параметров мы получим разбиение поверхности S на фрагменты . Соответственно такому разбиению прямоугольника параметров мы получим разбиение поверхности S на фрагменты  . Как известно, площадь такого фрагмента может быть получена по формуле . Как известно, площадь такого фрагмента может быть получена по формуле
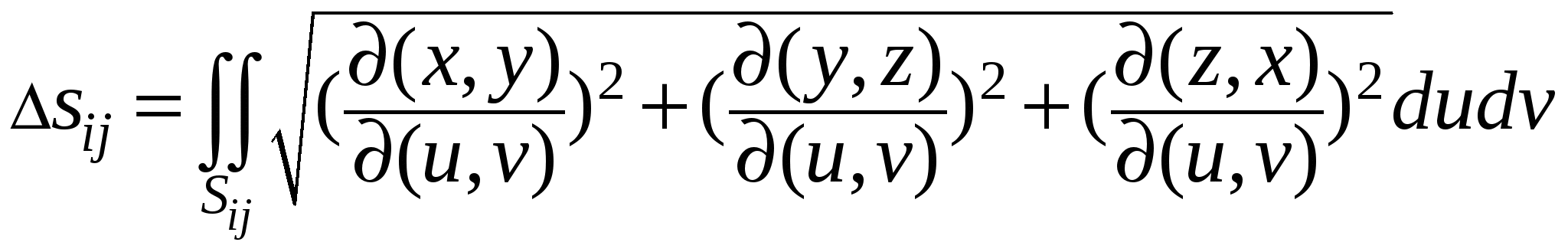 , ,
и согласно интегральной теореме о среднем,
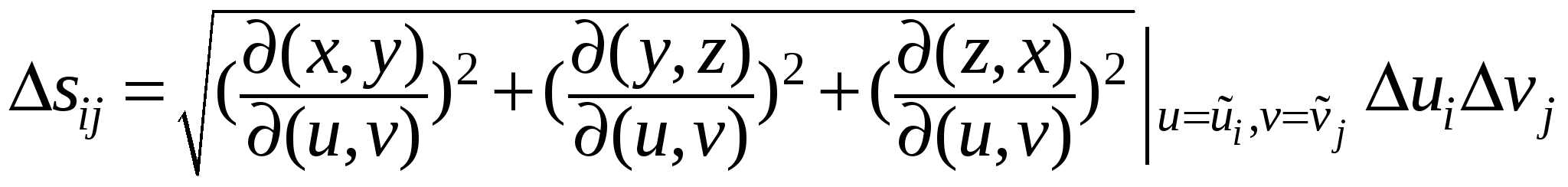
где 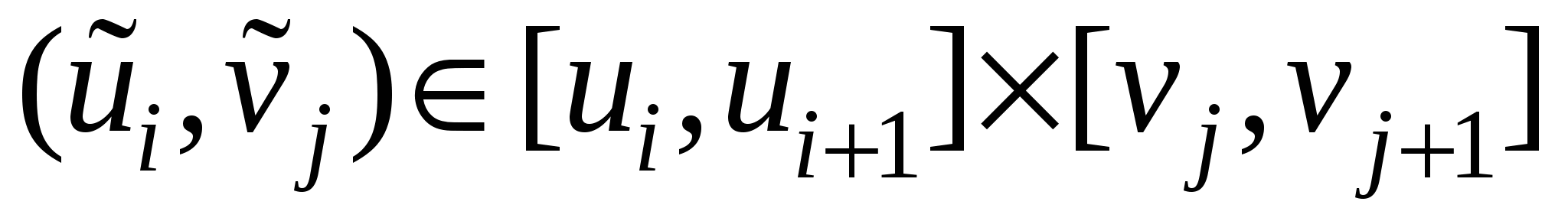 , , 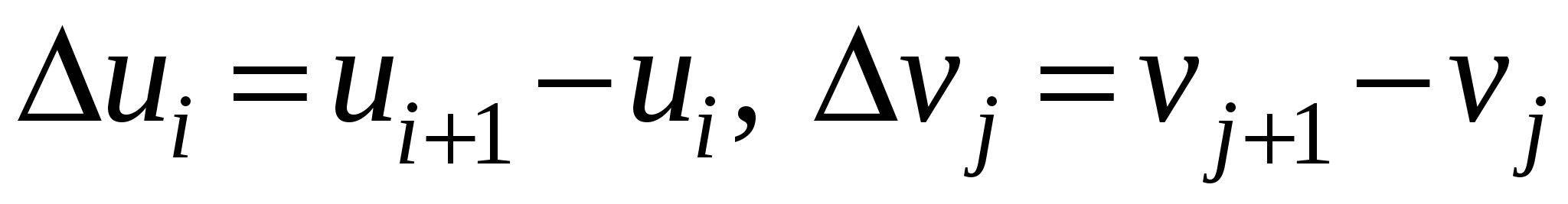 , , 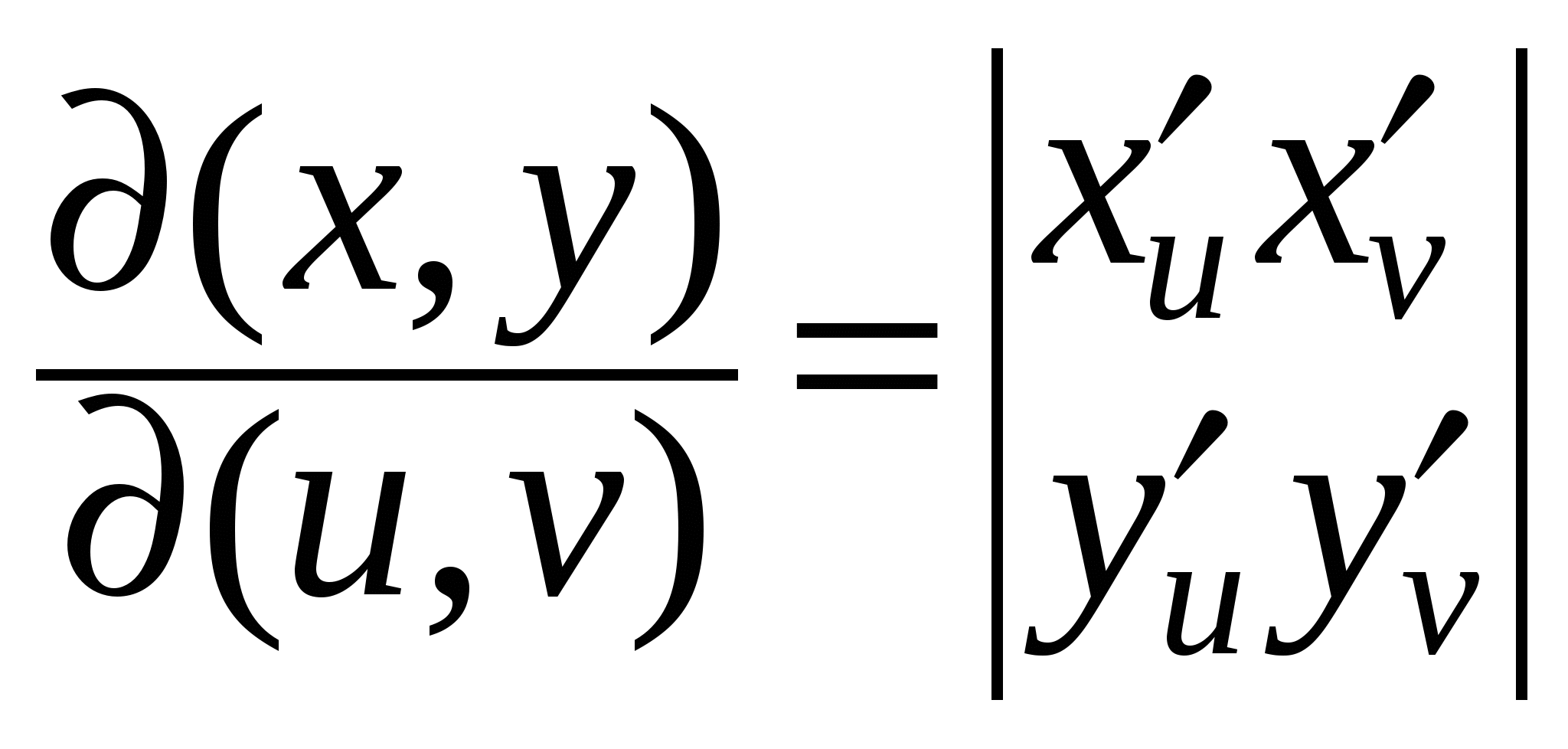 . Выберем теперь на поверхностном фрагменте . Выберем теперь на поверхностном фрагменте  в качестве точки с координатами в качестве точки с координатами 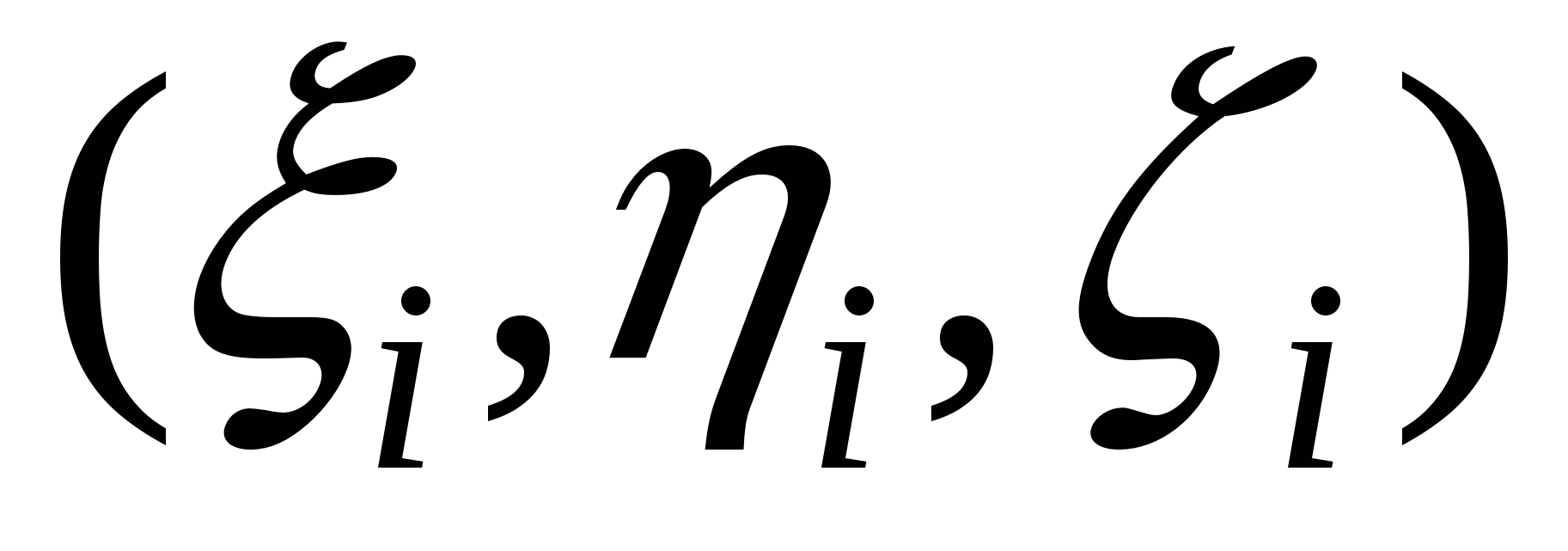 точку с координатами точку с координатами 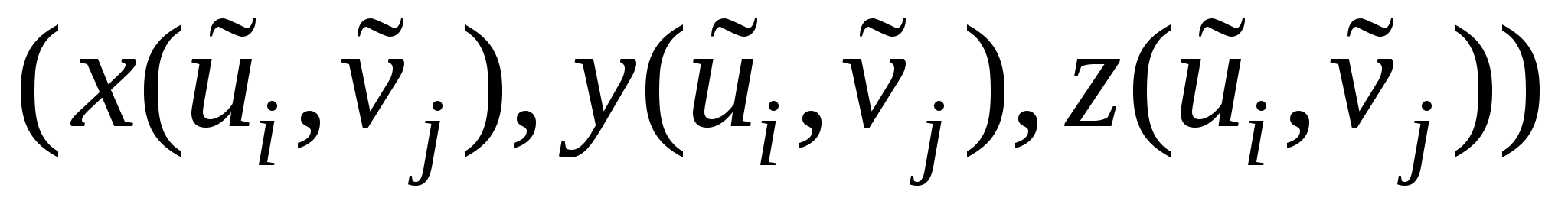 . Теперь так же, как в предыдущем параграфе, получим следующее выражение для поверхностного интеграла первого рода: . Теперь так же, как в предыдущем параграфе, получим следующее выражение для поверхностного интеграла первого рода:
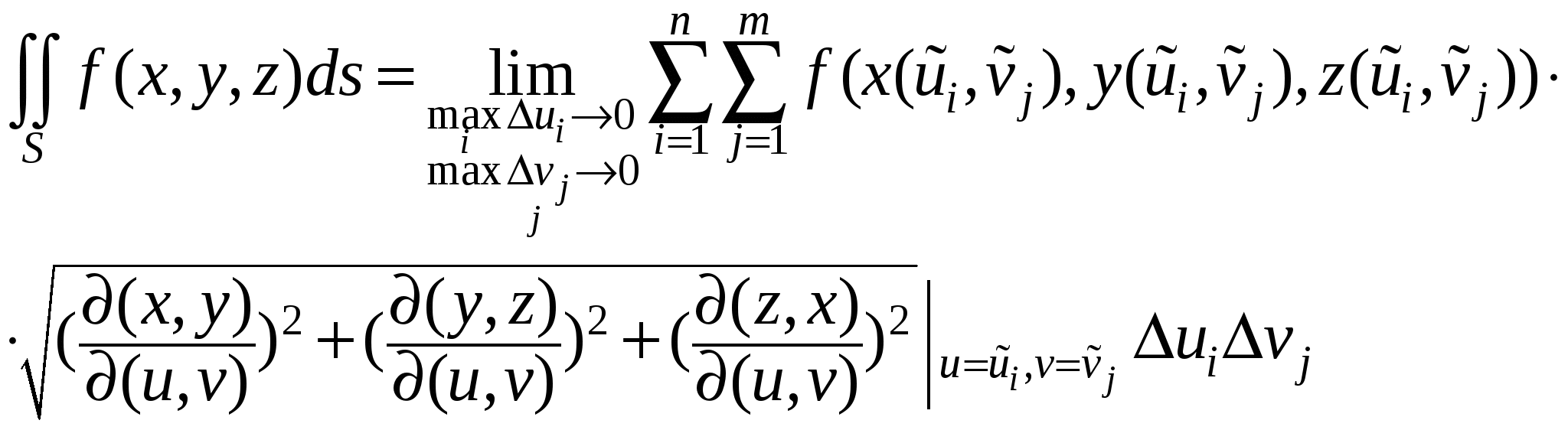 . .
Правая часть последнего выражения представляет собой интегральную сумму при интегрировании по прямоугольнику 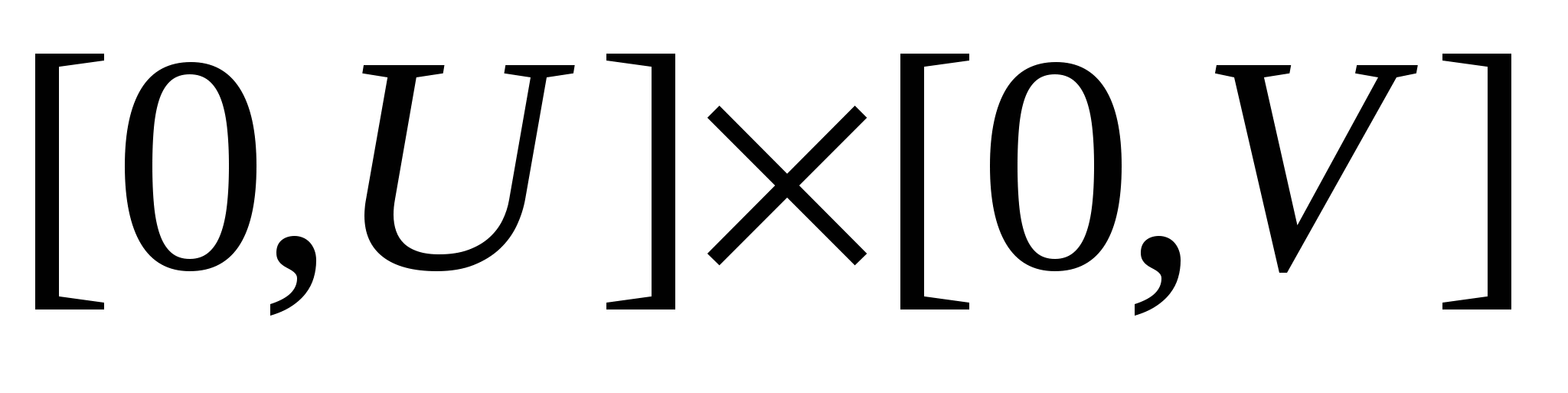 , поэтому, переходя к пределу, получим , поэтому, переходя к пределу, получим 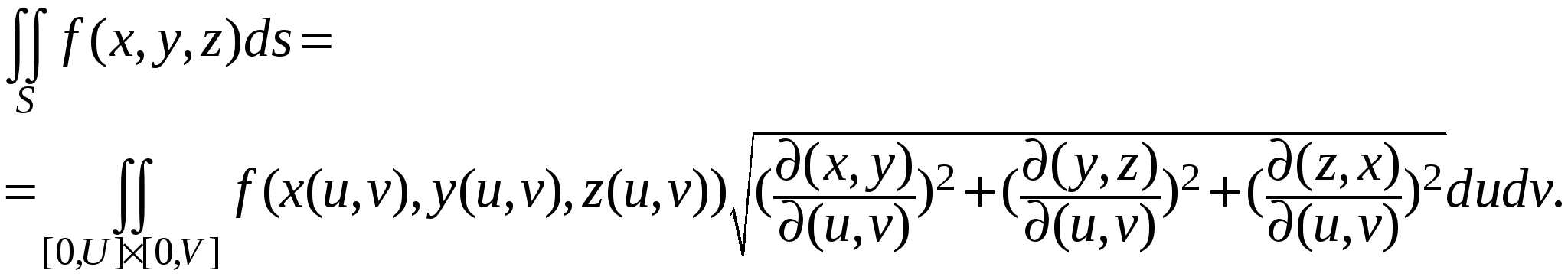
Заметим, что в плоскости изменения параметров может получиться не обязательно прямоугольник 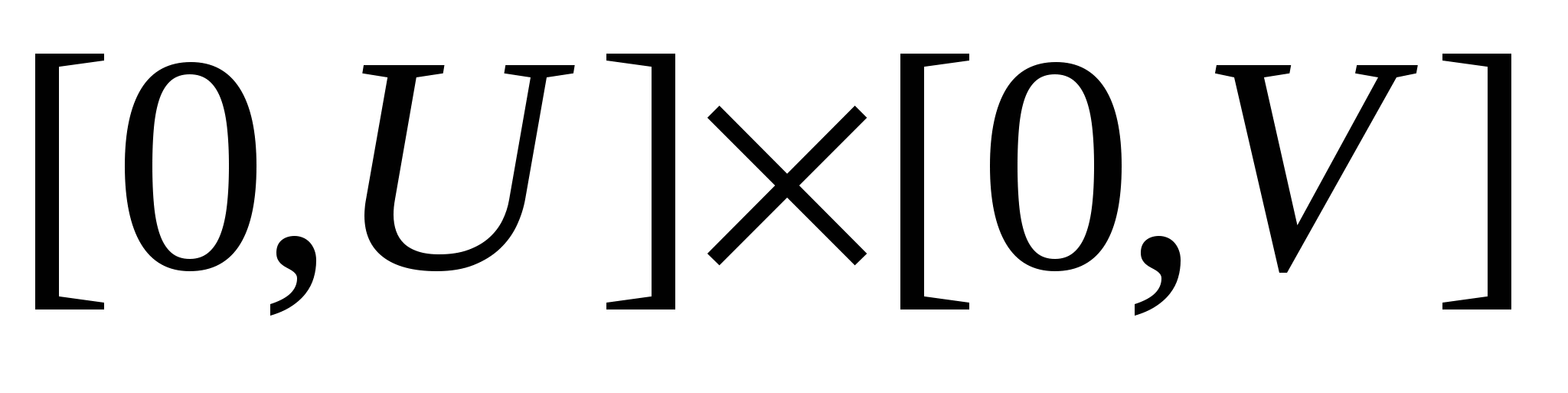 , а другая, более сложная, область. В любом случае приведенная формула позволяет от интеграла по площади поверхности перейти к двойному интегралу по области значений параметров. , а другая, более сложная, область. В любом случае приведенная формула позволяет от интеграла по площади поверхности перейти к двойному интегралу по области значений параметров.
П р и м е р ы.
Вычислить 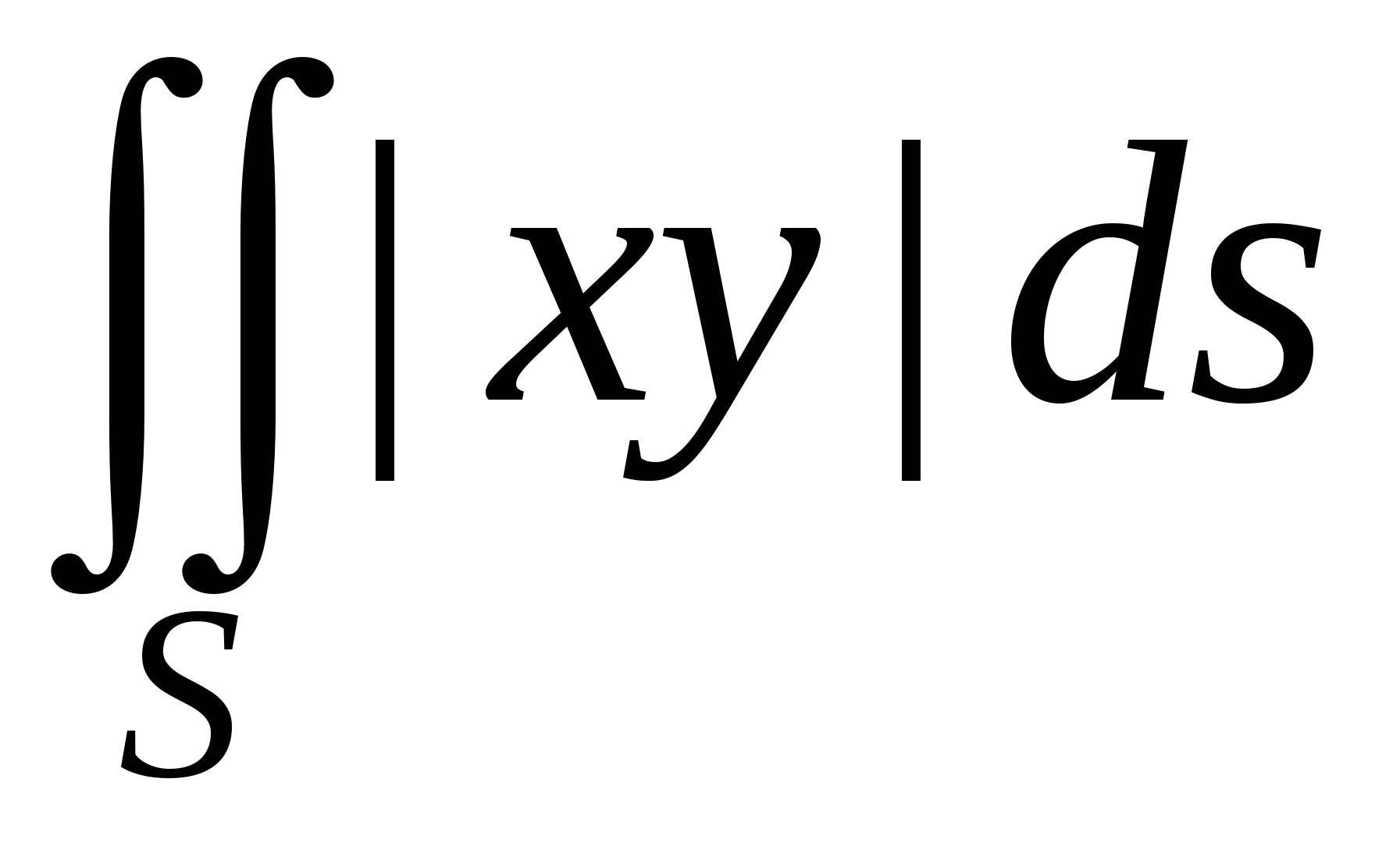 , где S – часть параболоида , где S – часть параболоида 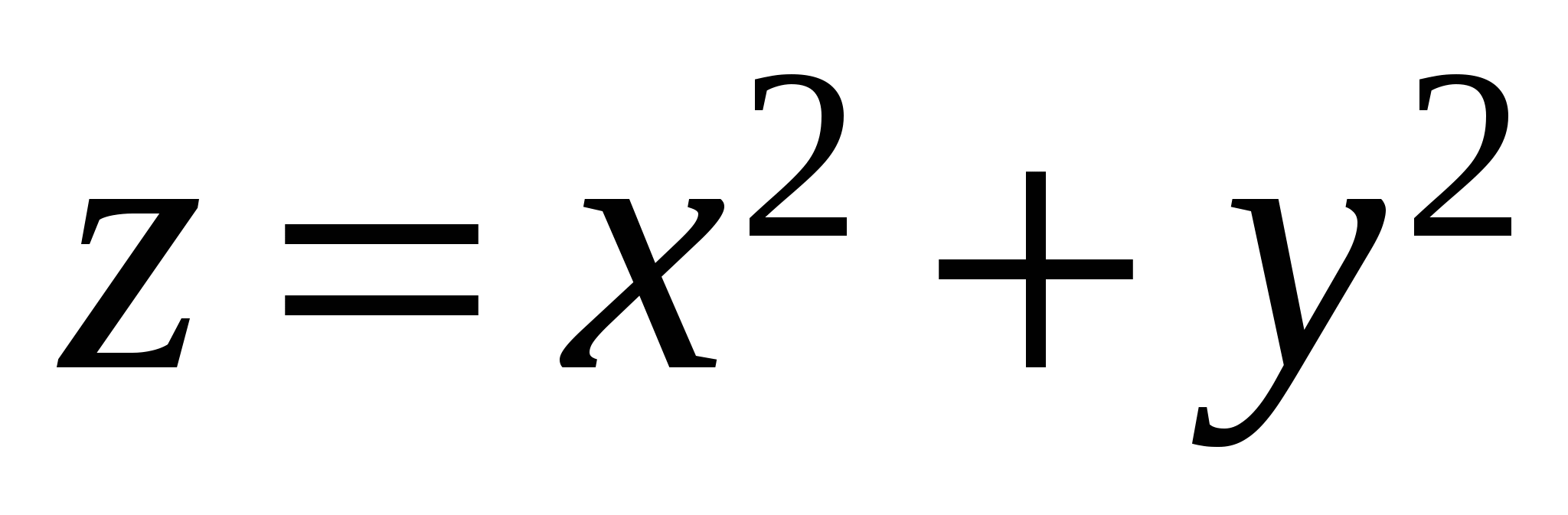 , отсекаемая плоскостью , отсекаемая плоскостью 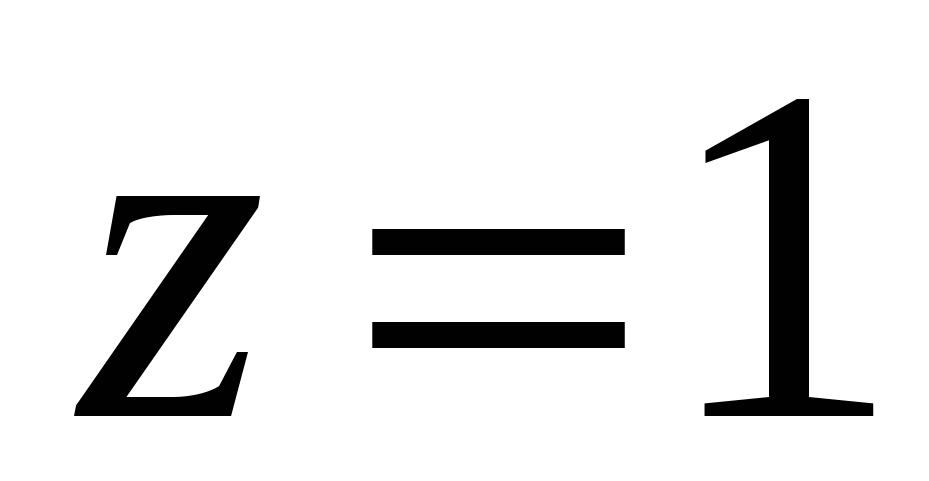 . .
Р е ш е н и е. Прежде всего, заметим, что проекцией данной поверхности S на плоскость XOY является круг 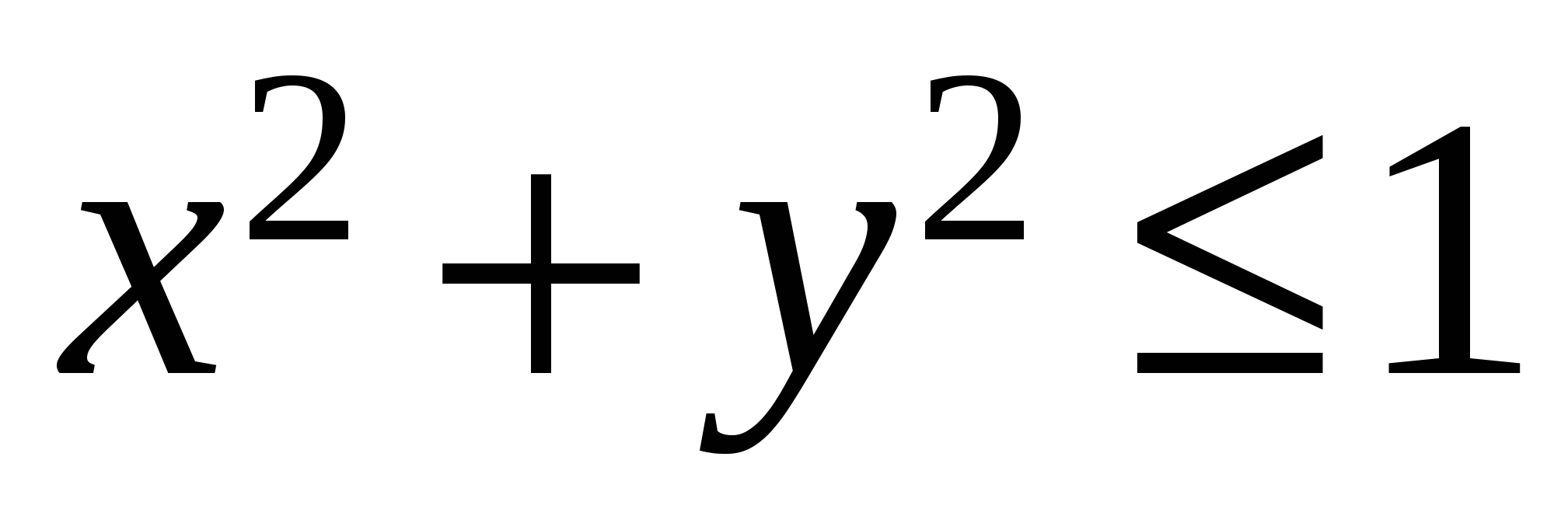 . Параметризуем уравнение поверхности с помощью полярных координат: . Параметризуем уравнение поверхности с помощью полярных координат:
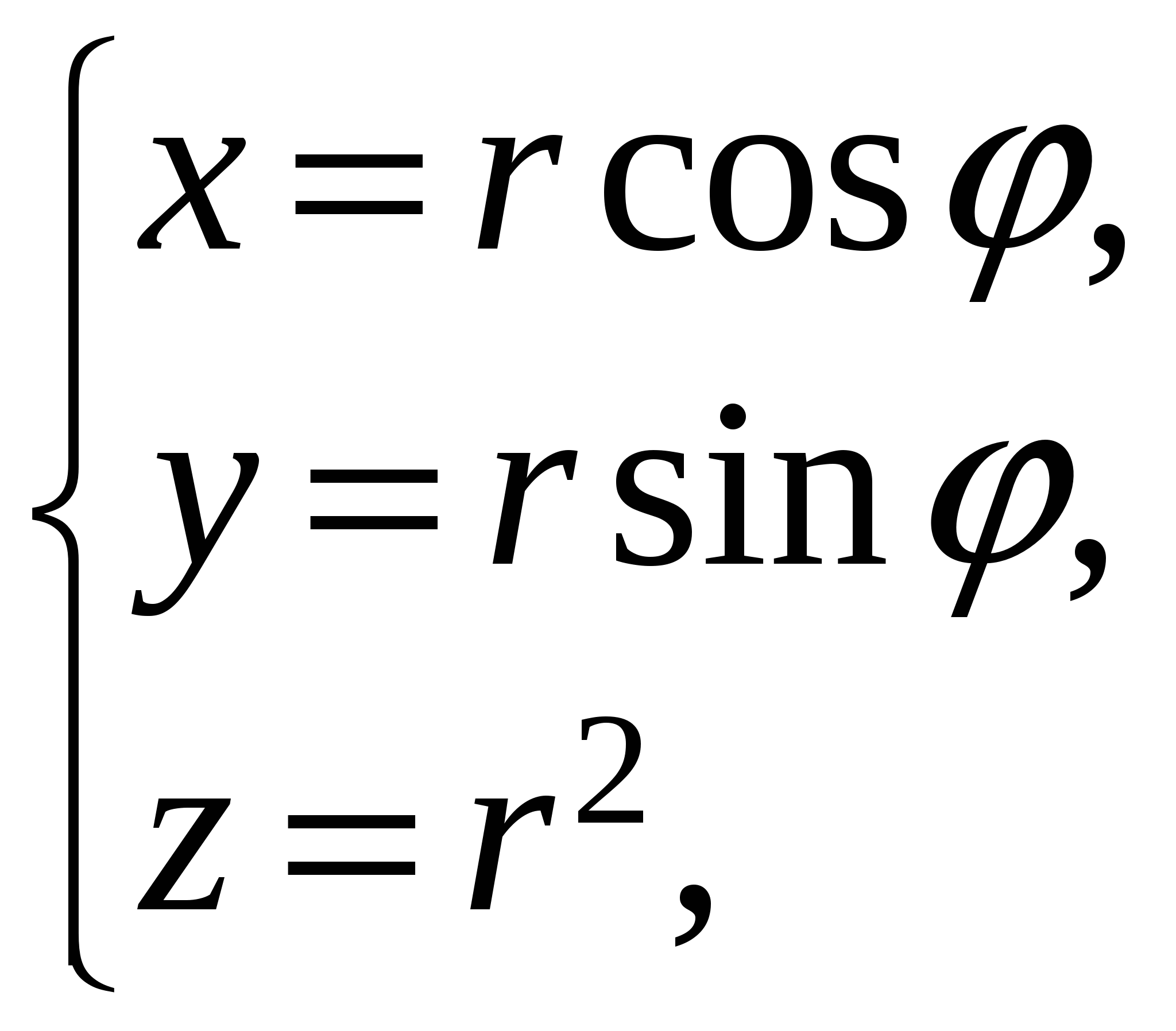 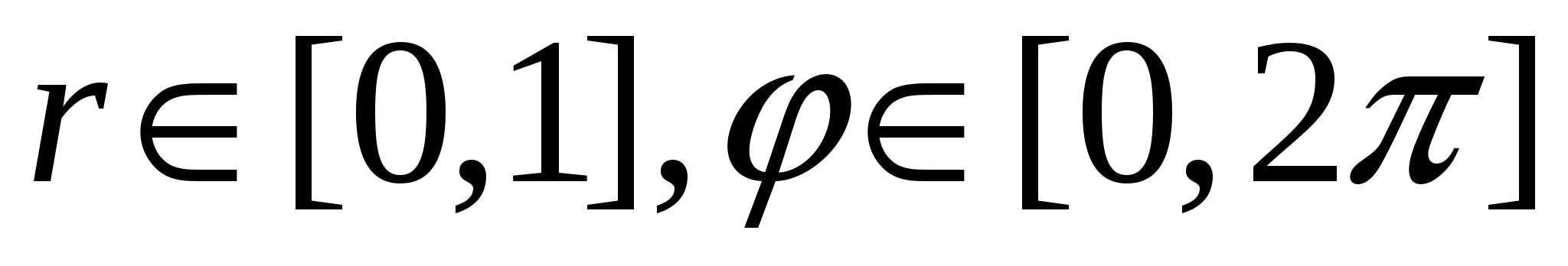 . .
Вычислим входящие в формулу якобианы: 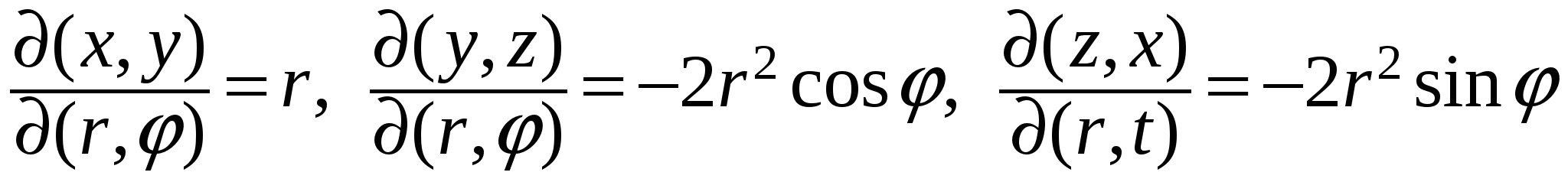 . .
Теперь получим представление исходного поверхностного интеграла через двойной интеграл по прямоугольнику значений параметров:
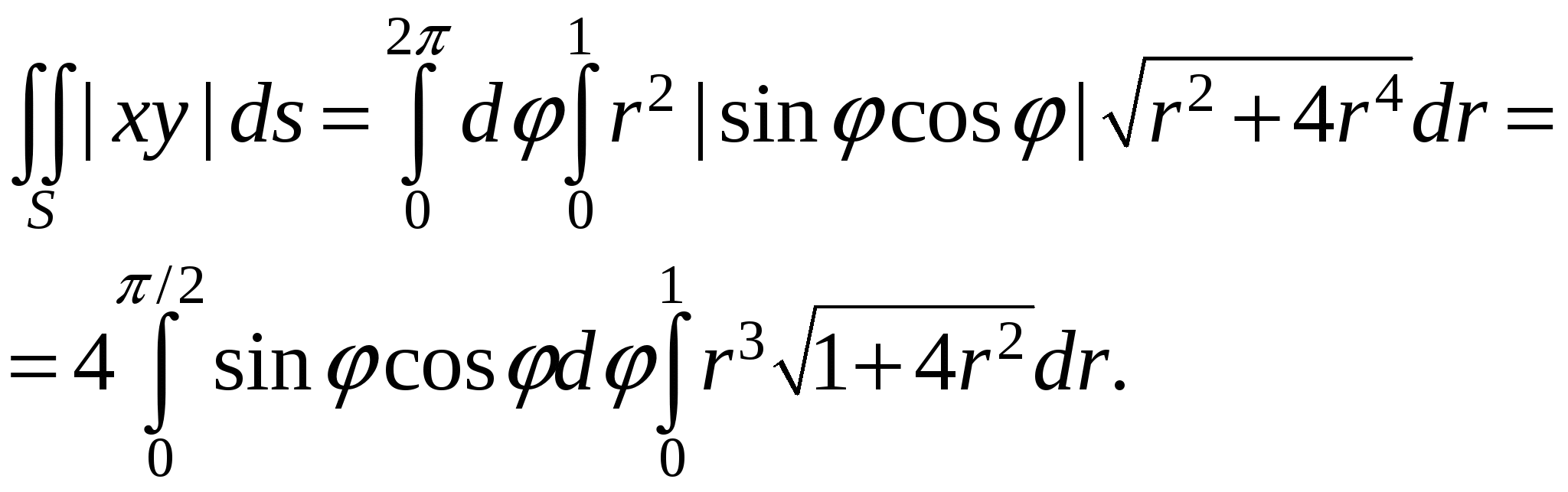
Таким образом, мы пришли к вычислению произведения двух интегралов по отрезкам.
Найти массу полусферы 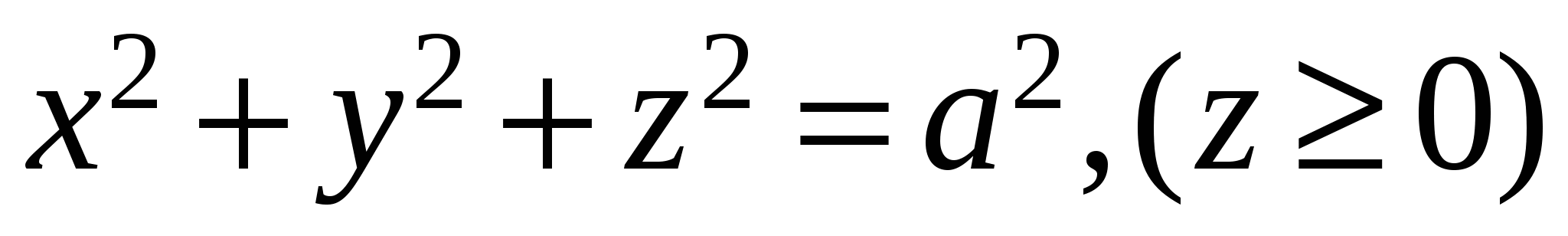 , плотность которой в каждой ее точке равна , плотность которой в каждой ее точке равна 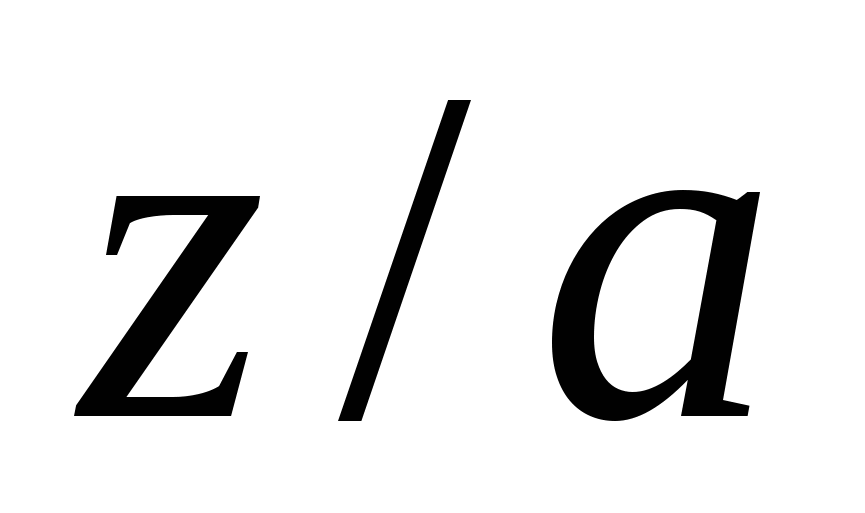 . .
|
 Скачать 0.51 Mb.
Скачать 0.51 Mb.
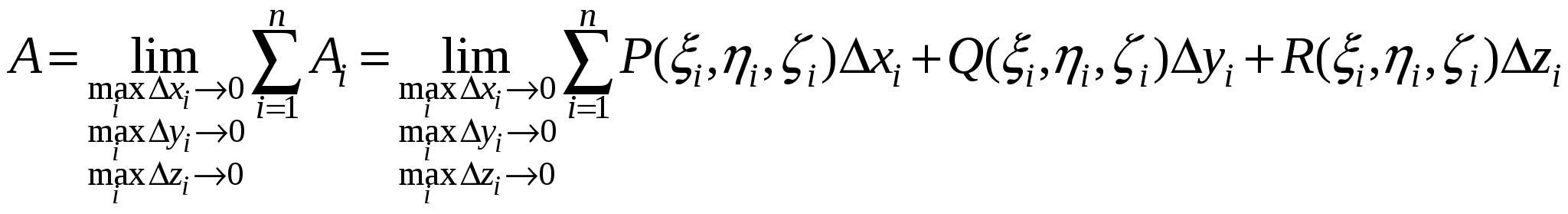 .
.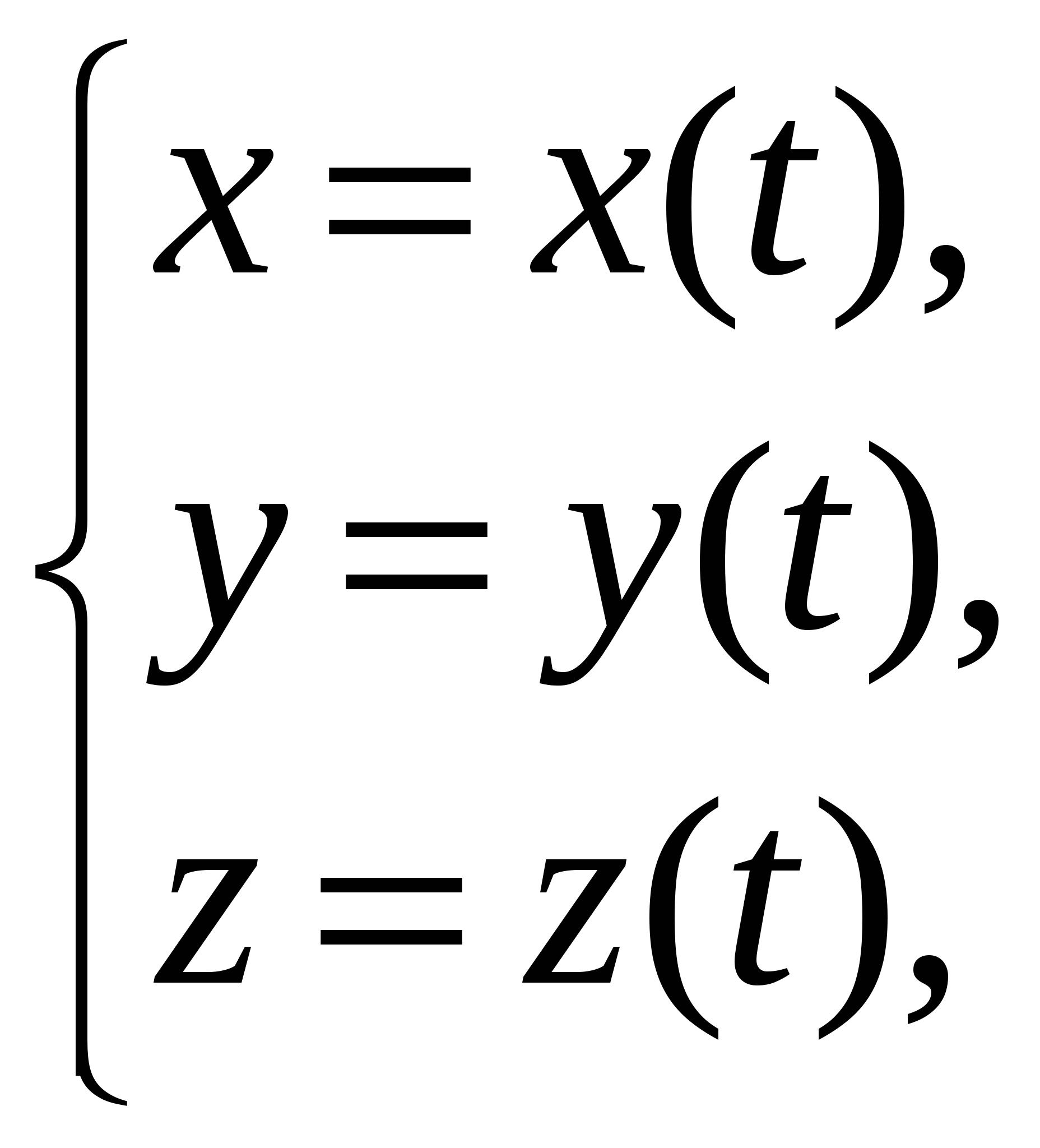
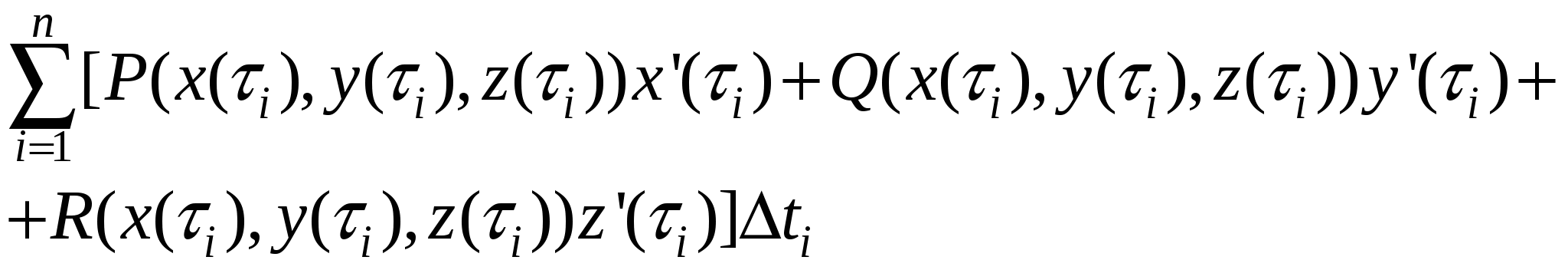 .
.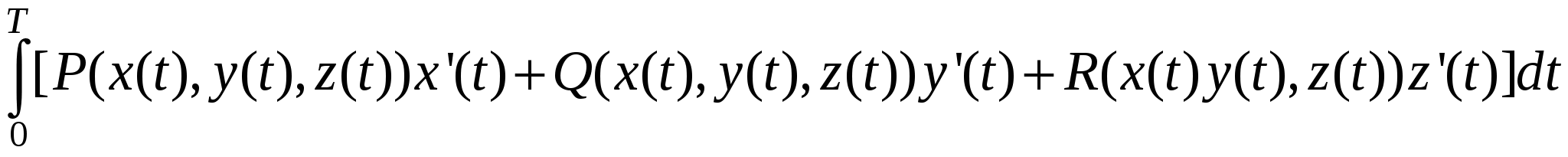 .
.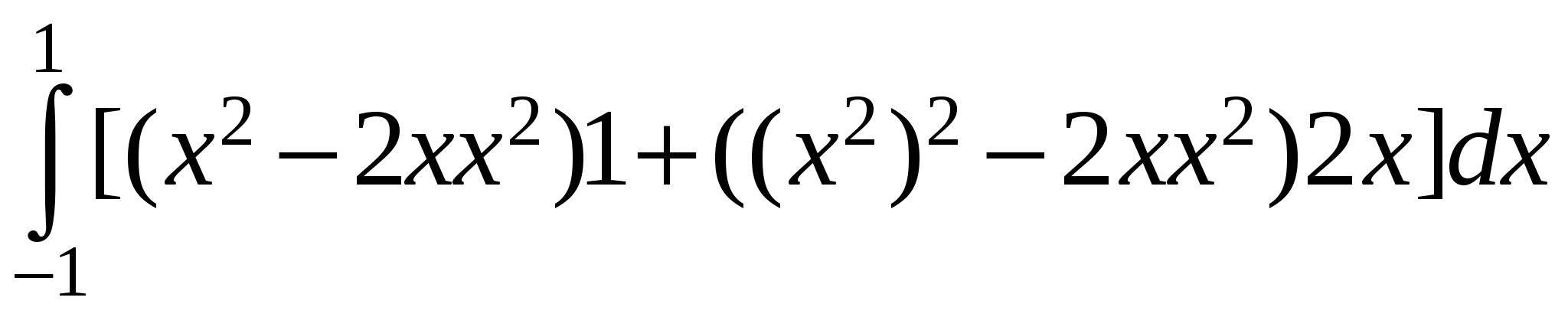 = =
= =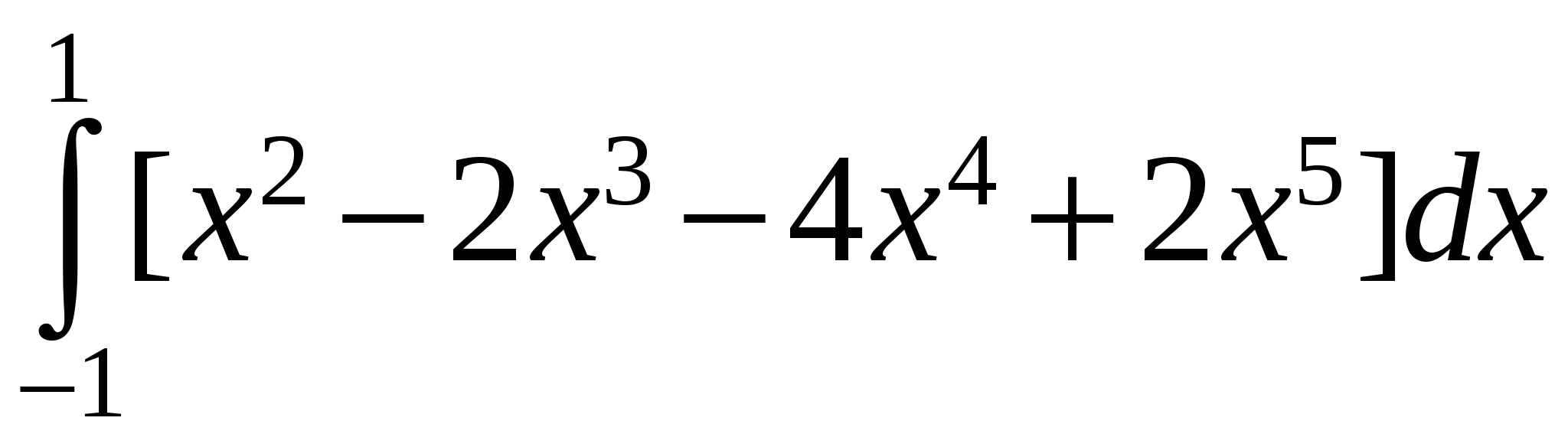 =
=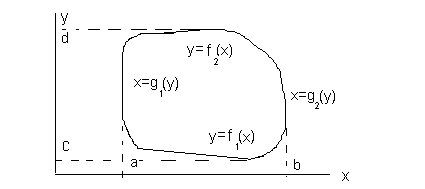
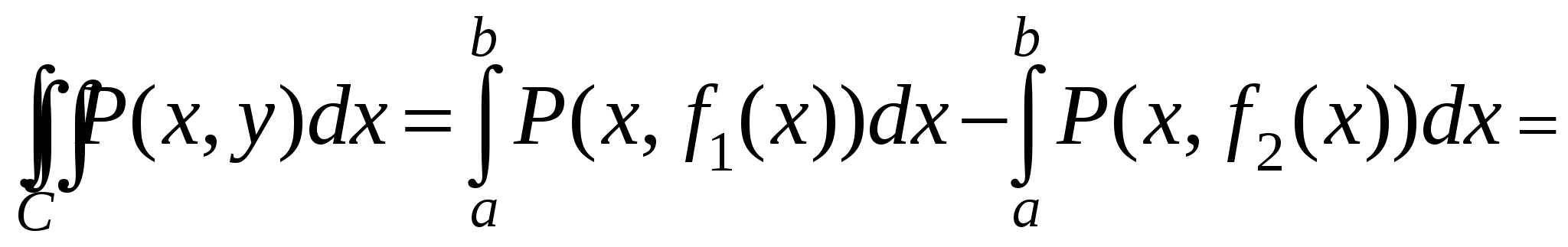
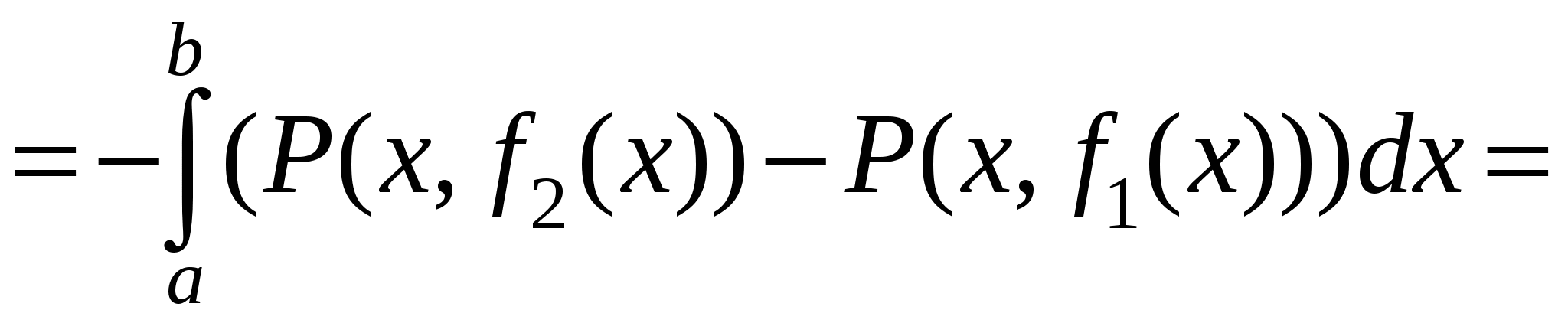
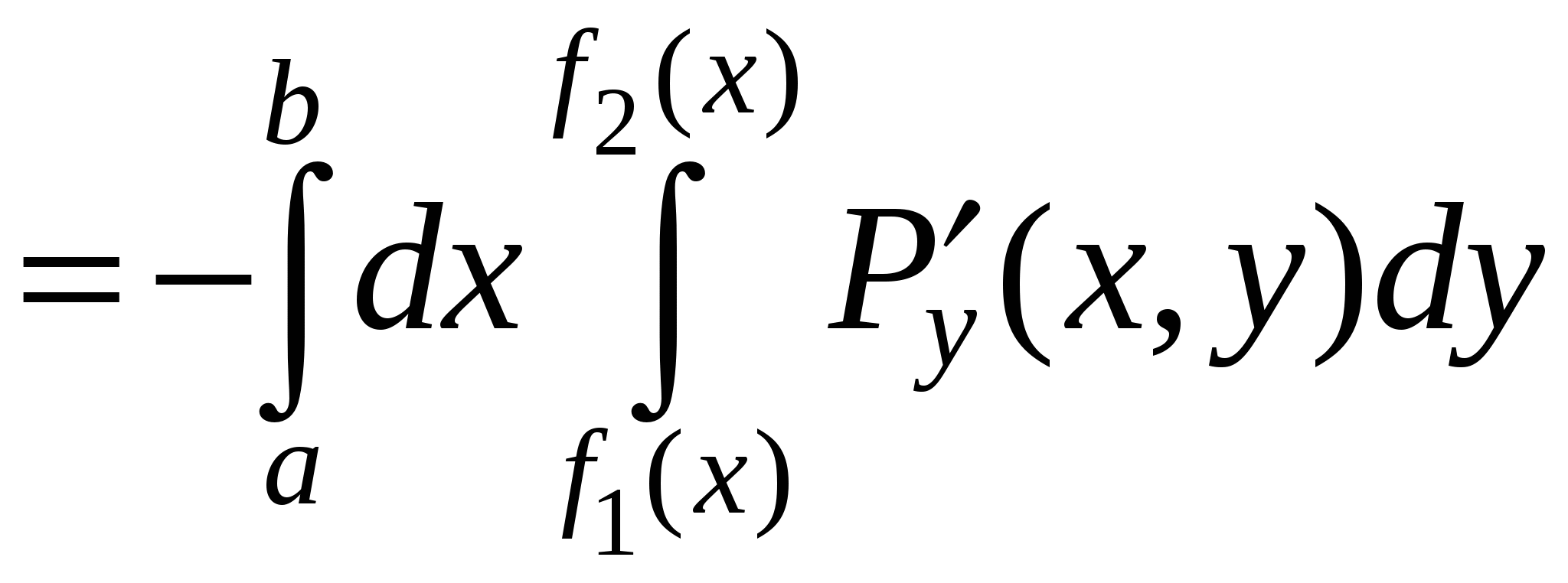
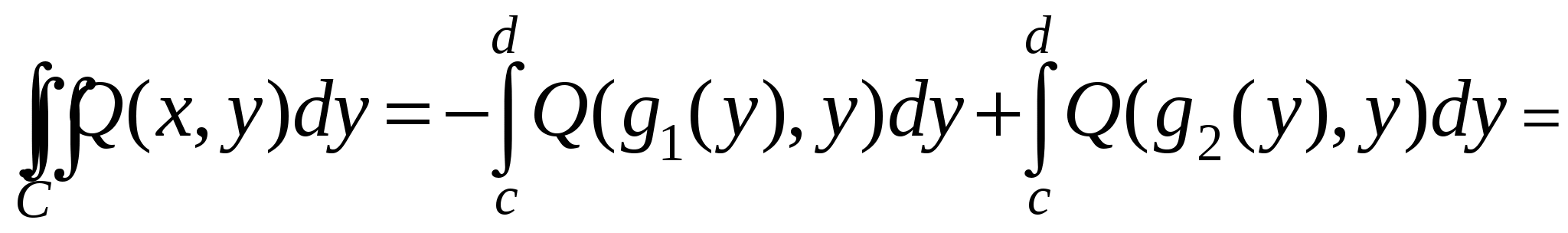
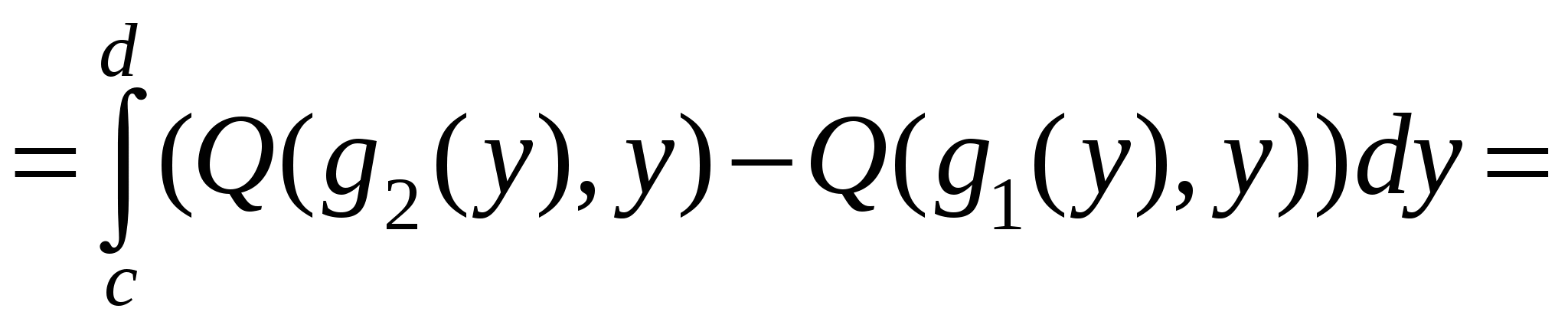
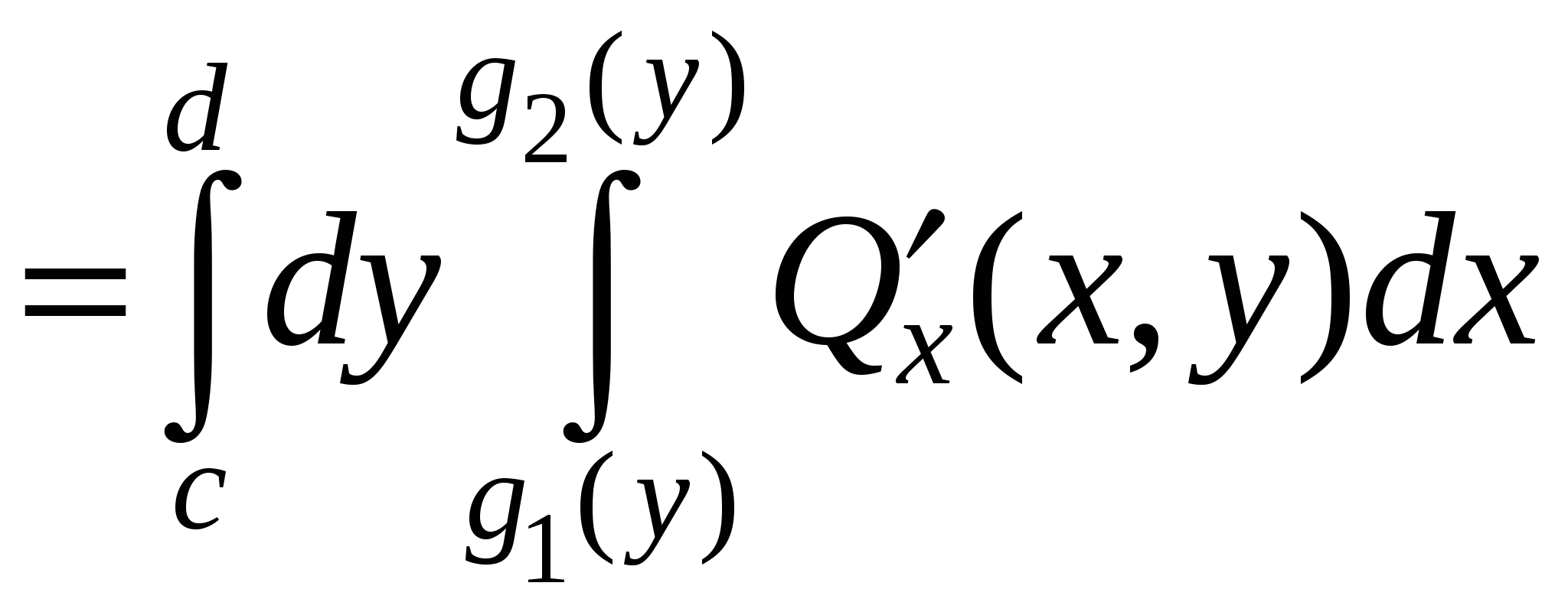

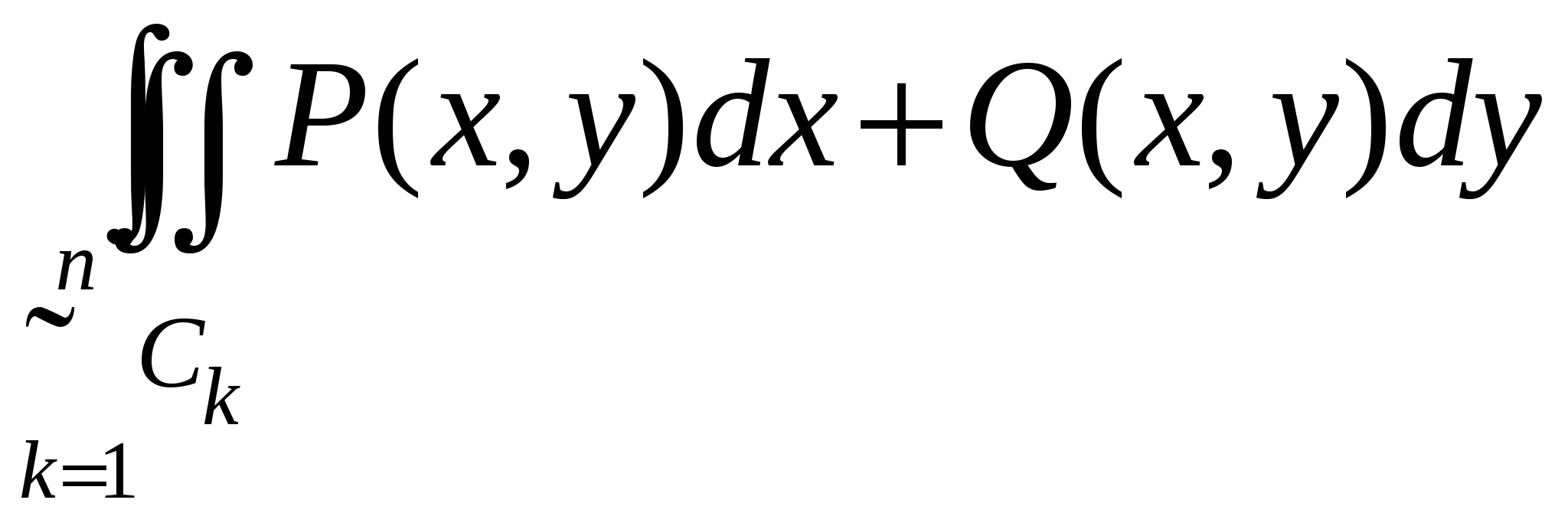 мы получим взаимное уничтожение интегралов вдоль прямолинейных отрезков внутри D.
мы получим взаимное уничтожение интегралов вдоль прямолинейных отрезков внутри D. 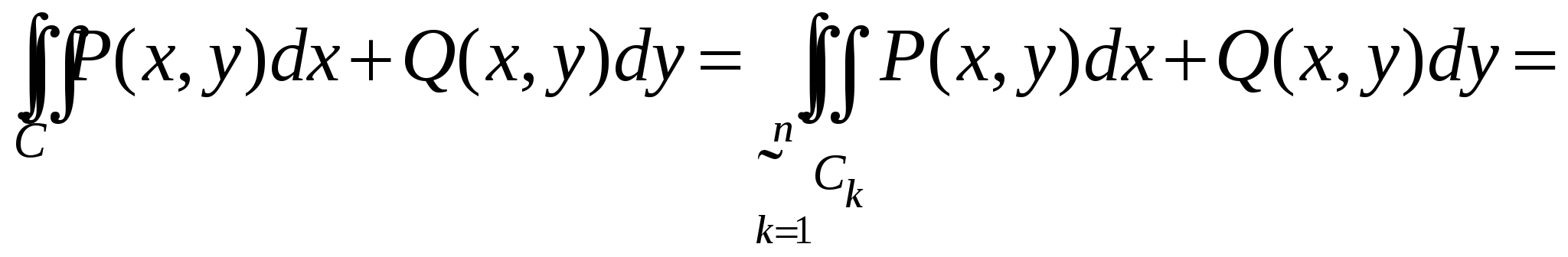
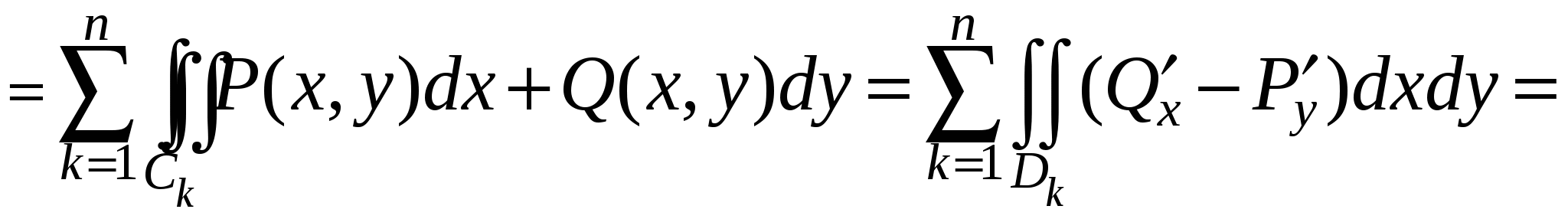


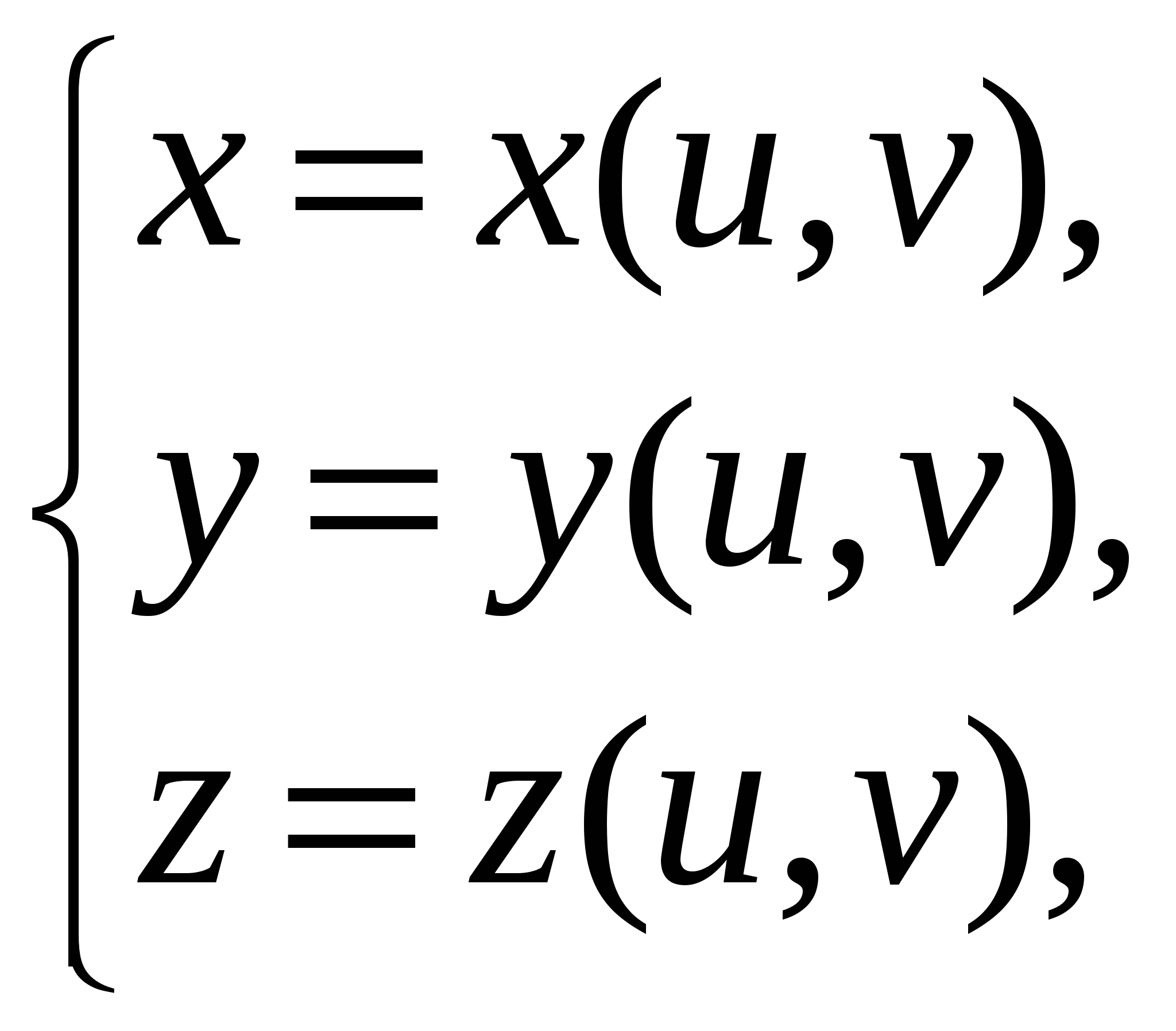
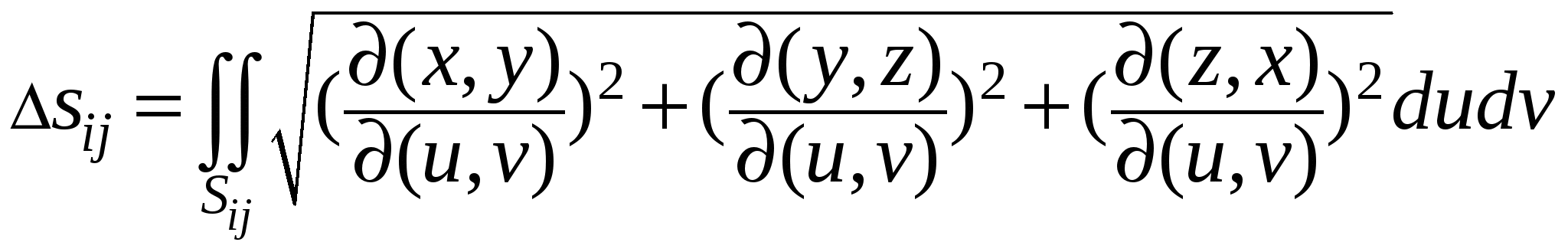 ,
, 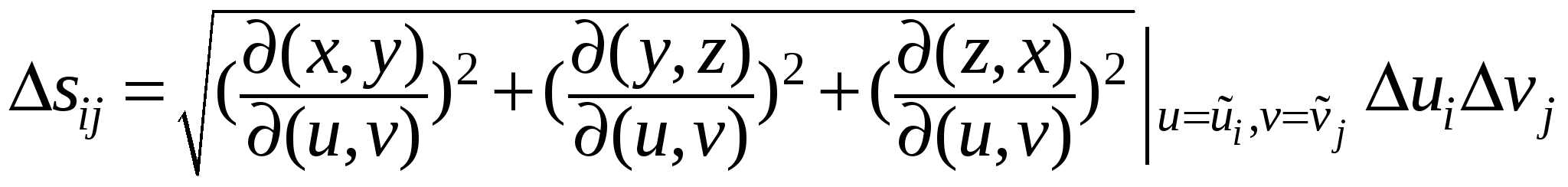
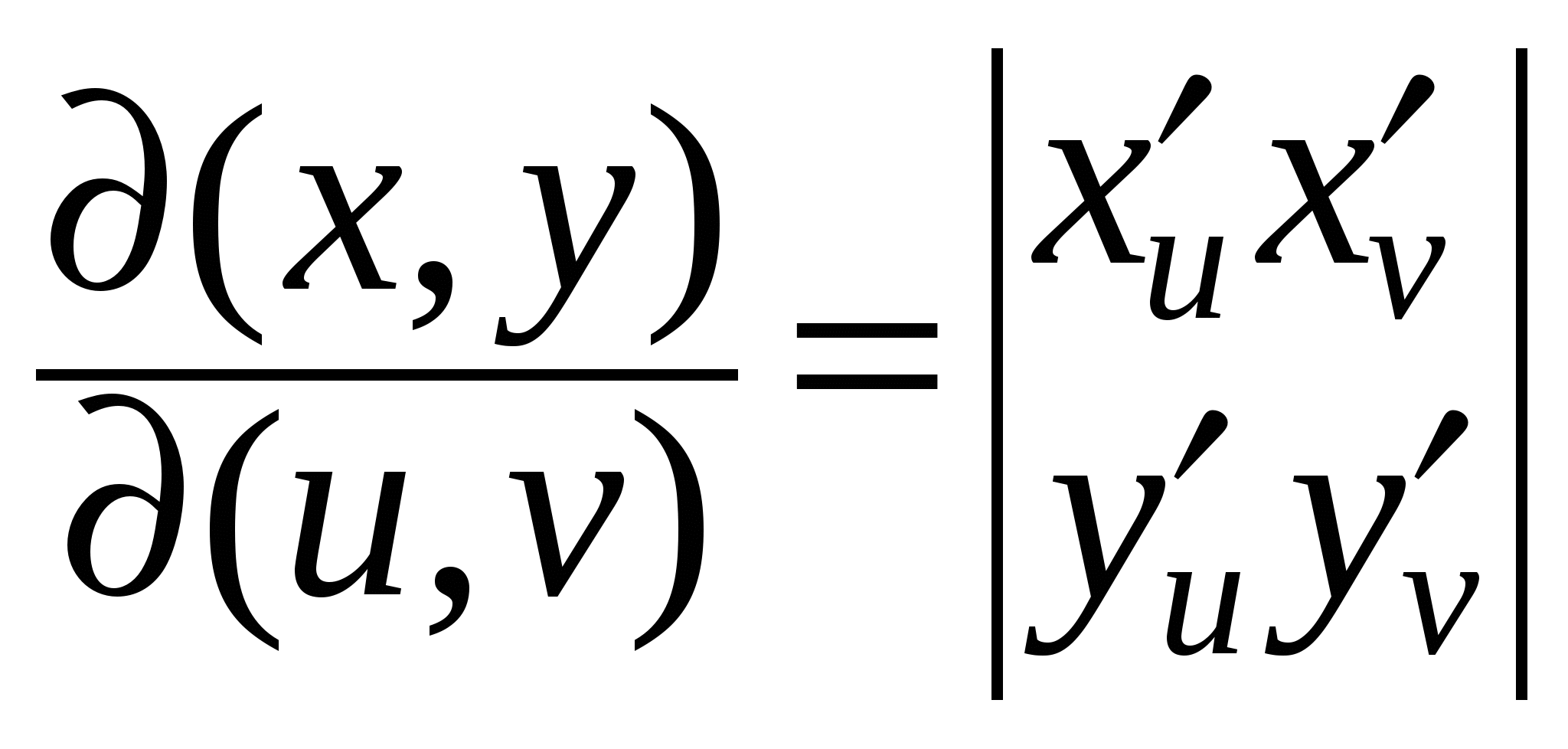 . Выберем теперь на поверхностном фрагменте
. Выберем теперь на поверхностном фрагменте 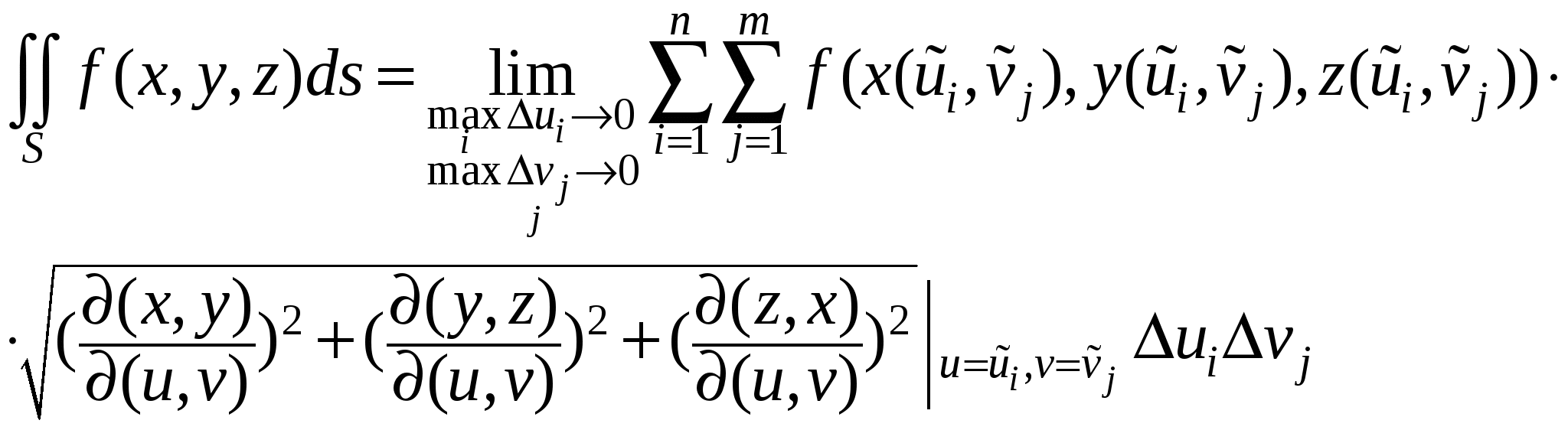 .
.