Теоретическая механика. ХАЙРУЛЛИН Д.Р. теор.мех. 2022. " Условия равновесия механических систем. Устойчивость равновесия"
 Скачать 76.74 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФГБОУ ВО «УДМУРТСКИЙ ГОСУДАРСТВКЕННЫЙ УНИВЕРСИТЕТ» ИНСТИТУТ НЕФТИ И ГАЗА ИМ. М.С. ГУЦЕРИЕВА КАФЕДРА: «РАЗРАБОТКА И ЭКСПЛУАТАЦИЯ НЕФТЯНЫХ И ГАЗОВЫХ МЕСТОРОЖДЕНИЙ» НАПРАВЛЕНИЕ 21.05.06: НЕФТЕГАЗОВЫЕ ТЕХНИКА И ТЕХНОЛОГИИ ПРОФИЛЬ «РАЗРАБОТКА И ЭКСПЛУАТАЦИЯ НЕФТЯНЫХ И ГАЗОВЫХ МЕСТОРОЖДЕНИЙ» РЕФЕРАТ ПО ДИСЦИПЛИНЕ “Теоретическая механика” НА ТЕМУ: “ Условия равновесия механических систем. Устойчивость равновесия” Выполнил студент группы 3C-21.05.06-25: Хайруллин Д.Р. Проверил преподаватель: Борисова Е.М ИЖЕВСК 2022 Условие равновесия механической системы Согласно принципу возможных перемещений (основному уравнению статики), для того, чтобы механическая система, на которую наложены идеальные, стационарные, удерживающие и голономные связи, находилась в равновесии, необходимо и достаточно, чтобы в этой системе были равны нулю все обобщенные силы:  где  - обобщенная сила, соответствующая j -ой обобщенной координате;s- число обобщенных координат в механической системе. Если для исследуемой системы были составлены дифференциальные уравнения движения в форме уравнений Лагранжа II - го рода, то для определения возможных положений равновесия достаточно приравнять обобщенные силы нулю и решить полученные уравнения относительно обобщенных координат. Если механическая система находится в равновесии в потенциальном силовом поле, то из уравнений (1) получаем следующие условия равновесия:  Следовательно, в положении равновесия потенциальная энергия имеет экстремальное значение. Не всякое равновесие, определяемое вышеприведенными формулами, может быть реализовано практически. В зависимости от поведения системы при отклонении от положения равновесия говорят об устойчивости или неустойчивости данного положения. Устойчивость равновесия Определение понятия устойчивости положения равновесия было дано в конце XIX века в работах русского ученого А. М. Ляпунова. Рассмотрим это определение. Для упрощения выкладок условимся в дальнейшем обобщенные координаты q1, q2,...,qsотсчитывать от положения равновесия системы:  где  Положение равновесия называется устойчивым, если для любого сколь угодно малого числа  можно найти такое другое число  , что в том случае, когда начальные значения обобщенных координат и скоростей не будут превышать  :  значения обобщенных координат и скоростей при дальнейшем движении системы не превысят  . Иными словами, положение равновесия системы q1 = q2 = ...= qs =0 называется устойчивым, если всегда можно найти такие достаточно малые начальные значения 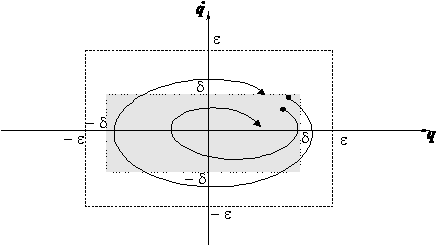 , при которых движение системы  не будет выходить из любой заданной сколь угодно малой окрестности положения равновесия  . Для системы с одной степенью свободы устойчивое движение системы можно наглядно изобразить в фазовой плоскости (рис.1). Для устойчивого положения равновесия движение изображающей точки, начинающееся в области [ ], не будет в дальнейшем выходить за пределы области  . Рис.1 Положение равновесия называетсяасимптотически устойчивым, если с течением времени система будет приближаться к положению равновесия, то есть  Определение условий устойчивости положения равновесия представляет собой достаточно сложную задачу, поэтому ограничимся простейшим случаем: исследованием устойчивости равновесия консервативных систем . Достаточные условия устойчивости положений равновесия для таких систем определяются теоремой Лагранжа - Дирихле: положение равновесия консервативной механической системы устойчиво, если в положении равновесия потенциальная энергия системы имеет изолированный минимум. Потенциальная энергия механической системы определяется с точностью до постоянной. Выберем эту постоянную так, чтобы в положении равновесия потенциальная энергия равнялась нулю: П(0)=0. Тогда для системы с одной степенью свободы достаточным условием существования изолированного минимума, наряду с необходимым условием (2), будет условие  Так как в положении равновесия потенциальная энергия имеет изолированный минимум и П(0)=0, то в некоторой конечной окрестности этого положения П(q)=0. Функции, имеющие постоянный знак и равные нулю только при нулевых значениях всех своих аргументов, называются знакоопределенными. Следовательно, для того, чтобы положение равновесия механической системы было устойчивым необходимо и достаточно, чтобы в окрестности этого положения потенциальная энергия была положительно определенной функцией обобщенных координат. Для линейных систем и для систем, которые можно свести к линейным при малых отклонениях от положения равновесия (линеаризовать), потенциальную энергию можно представить в виде квадратичной формы обобщенных координат 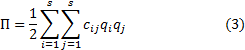 где  - обобщенные коэффициенты жесткости.Обобщенные коэффициенты являются постоянными числами, которые могут быть определены непосредственно из разложения потенциальной энергии в ряд или по значениям вторых производных от потенциальной энергии по обобщенным координатам в положении равновесия: Из формулы (4) следует, что обобщенные коэффициенты жесткости симметричны относительно индексов  Для того, чтобы выполнялись достаточные условия устойчивости положения равновесия, потенциальная энергия должна быть положительно определенной квадратичной формой своих обобщенных координат. В математике существует критерий Сильвестра, дающий необходимые и достаточные условия положительной определенности квадратичных форм: квадратичная форма (3) будет положительно определенной, если определитель, составленный из ее коэффициентов, и все его главные диагональные миноры будут положительными, т.е. если коэффициенты  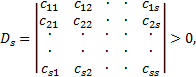будут удовлетворять условиям  . . . . .  В частности, для линейной системы с двумя степенями свободы потенциальная энергия и условия критерия Сильвестра будут иметь вид    Аналогичным образом можно провести исследование положений относительного равновесия, если вместо потенциальной энергии ввести в рассмотрение потенциальную энергию приведенной системы. Пример определения положений равновесия и исследования их устойчивости 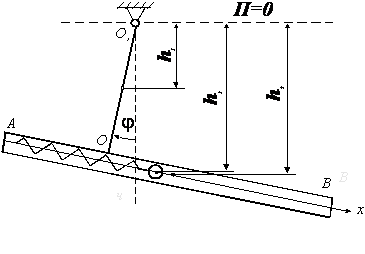 Рис.2 Рассмотрим механическую систему, состоящую из трубки AB, которая стержнем OO1 соединена с горизонтальной осью вращения, и шарика, который перемещается по трубке без трения и связан с точкой A трубки пружиной (рис.2). Определим положения равновесия системы и оценим их устойчивость при следующих параметрах: длина трубки l2= 1м,длина стержняl1 =0,5м. длина недеформированной пружины l0 = 0,6 м , жесткость пружины c = 100 Н/м.Масса трубки m2 = 2 кг , стержня - m1 = 1 кги шарика - m3 = 0,5 кг. Расстояние OA равно l3 = 0,4 м. Запишем выражение для потенциальной энергии рассматриваемой системы. Она складывается из потенциальной энергии трех тел, находящихся в однородном поле силы тяжести, и потенциальной энергии деформированной пружины. Потенциальная энергия тела в поле силы тяжести равна произведению веса тела на высоту его центра тяжести над плоскостью, в которой потенциальная энергия считается равной нулю. Пусть потенциальная энергия равна нулю в плоскости, проходящей через ось вращения стержня OO1 , тогда для сил тяжести    Для силы упругости потенциальная энергия определяется величиной деформации   Найдем возможные положения равновесия системы. Значения координат в положениях равновесия есть корни следующей системы уравнений. 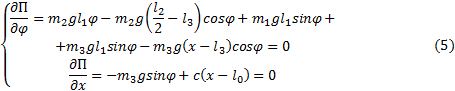 Подобную систему уравнений можно составить для любой механической системы с двумя степенями свободы. В некоторых случаях можно получить точное решение системы. Для системы (5) такого решения не существует, поэтому корни надо искать с помощью численных методов. Решая систему трансцендентных уравнений (5), получаем два возможных положения равновесия:   Для оценки устойчивости полученных положений равновесия найдем все вторые производные от потенциальной энергии по обобщенным координатам и по ним определим обобщенные коэффициенты жесткости.    Тогда для первого положения равновесия    Воспользуемся критерием Сильвестра   Для второго найденного положения равновесия   Список литературы Арнольд В. И. Математические методы классической механики. — 5-е изд., стереотипное. — М.: Едиториал УРСС, 2003. — 416 с. — 1500 экз. — ISBN 5-354-00341-5 Ландау, Л. Д., Лифшиц, Е. М. Механика. — Издание 4-е, исправленное. — М.: Наука, 1988. — 215 с. — («Теоретическая физика», том I). — ISBN 5-02-013850-9 Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7 Сивухин Д. В. Общий курс физики. — Издание 4-е. — М.: Физматлит, 2002. — Т. I. Механика. — 792 с. — ISBN 5-9221-0225-7 https://infopedia.su/9x690d.html https://www.evkova.org/teoremyi-ob-izmenenii-kolichestva-dvizheniya-i-o-dvizhenii-tsentra-mass-v-teoreticheskoj-mehanike https://wreferat.baza-referat.ru/Количество_движения |