Тест По Высшой Математике Для Дистанционников (Дьячков А. М.). Тест По Высшой Математике Для Дистанционников (Дьячков А. М. 1 1 e 1x e 1x ln x cos x2
 Скачать 481 Kb. Скачать 481 Kb.
|
|
x(t) = 3 + 2 e-t *cos2t + 1 e-t * sin 2t + 5 5 5 Решить дифференциальные уравнение: x(t) = (t + 1)e-t. + Решить дифференциальные уравнение: 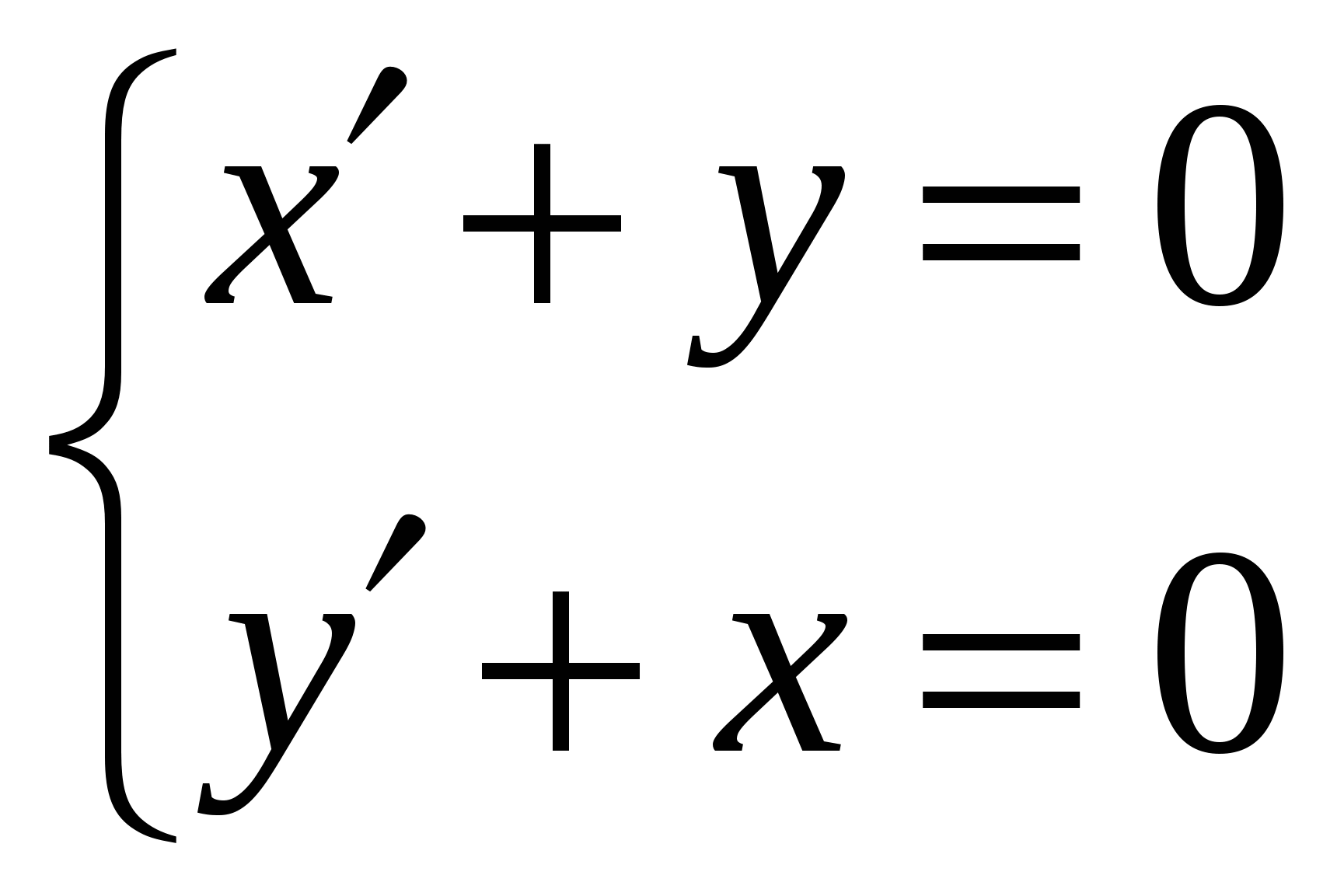 , , x(t) = et, y(t) = - et. + Найти решение уравнения: y3 = - │3cos3x (C+tgx)│-1 + Найти решение уравнения: y = cx + x2. + Найти решение уравнения: Найти решение уравнения: Найти решение уравнения: Найти решение уравнения: y = 1+ex – xe2x + c1e2x + c2e3x. + Найти решение уравнения: y=ex(c1x+c2x2+х2) + Найти решение уравнения: y = (c1 cos3x + c2 sin3x) ex + 1/37 (sin3x + 6cos3x) + ex/9. + Найти решение уравнения: y = (c2x + x3/6)ех. + Найти решение уравнения: y = c1e-x + c2e-2x – 2/5 (3sin2x + cos2x).+ Найти решение уравнения: y= c*sinПx. + Найти решение уравнения: y= c1e2x + c2e3x. + Найти решение уравнения: y = ½ (ex – e-x).+ Найти решение уравнения: y= 4ex + e 4x. + Найти решение уравнения: y= x + c1. + x + c2 Найти решение уравнения: x2=y2(C-y2).+ Найти решение уравнения: x= y3 – 4 – 1 lny. + 9 3 Найти решение уравнения: y2=cx2 – 2x. + Найти решение уравнения: y= - e-x * ln│x-1│.+ Найти решение уравнения: y= ____1____ нет (x – 1)cosx Найти интеграл дифференциального уравнения: Найти интеграл дифференциального уравнения: cosB = Ccosa. + Найти интеграл дифференциального уравнения: Найти интеграл дифференциального уравнения: (ey +1)ex =c. + Найти интеграл дифференциального уравнения: (x – 1)2 + y2 =c2. + Найти интеграл дифференциального уравнения: y = e y/x -1.+ Найти интеграл дифференциального уравнения: arctg y/x = ln c√x2 + y2. + Найти интеграл дифференциального уравнения: x = (y-x)*lnc(y-x).+ Найти интеграл дифференциального уравнения: 3y3 = 8(x2 – y2). + Найти интеграл дифференциального уравнения: ln│cx│= - e –y/x. + Найти решение дифференциального уравнения: y = c2 - cos (x + c1). + Найти решение дифференциального уравнения: y = c1ln│x│- x2/4 + c2 + Найти решение дифференциального уравнения: y3 – y = 3x.+ Найти решение дифференциального уравнения: (y – 1)2 = 8(x-1)3(3x+2)2. + Найти решение дифференциального уравнения: y = с1ес2x + 1/c2 + Вычислить интеграл: П/2а. + Вычислить интеграл: │Z│=4 Пi +. Вычислить интеграл: 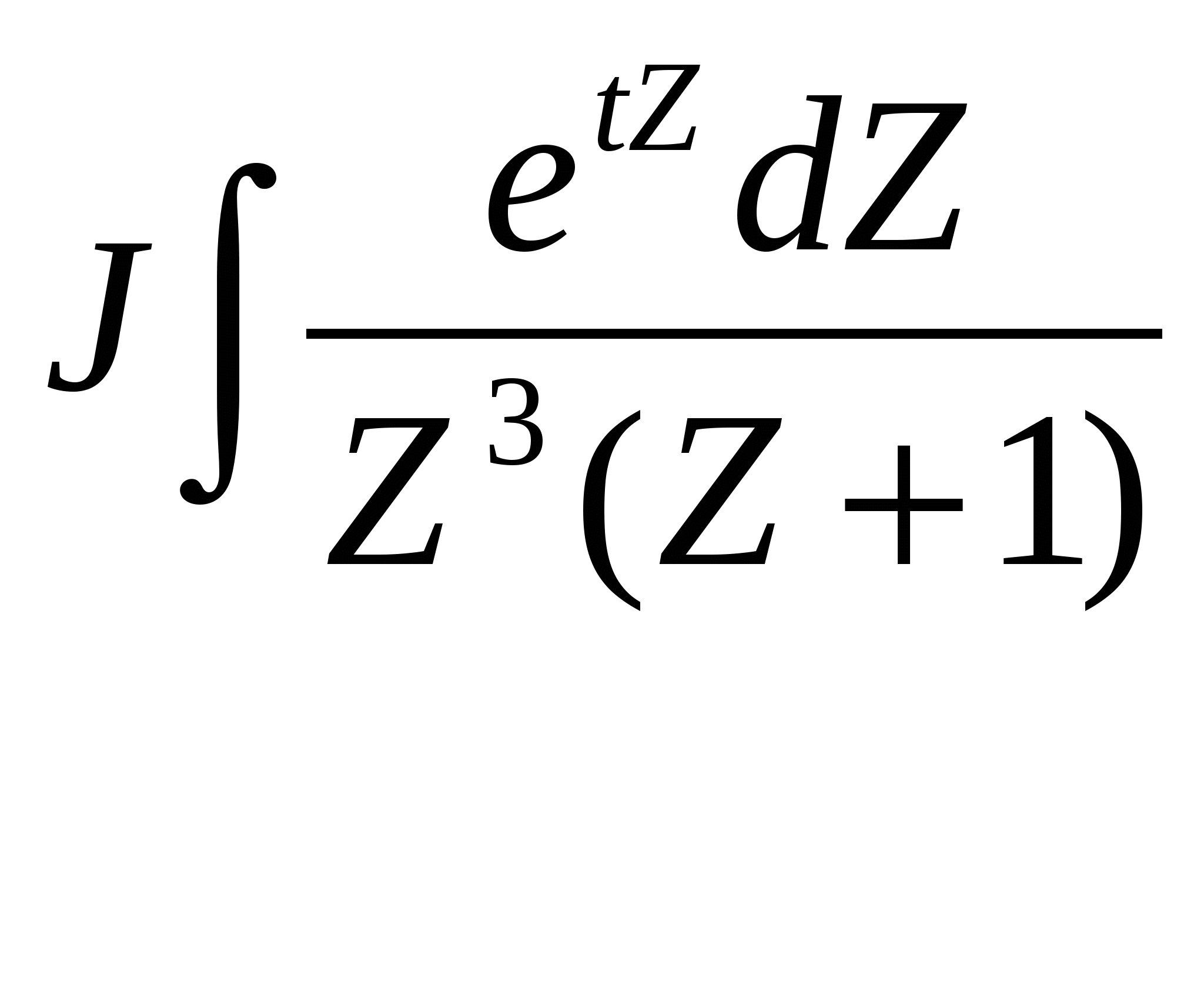 . .│Z│=2 i *2П (1/2 – e-1) + Вычислить интеграл: 7/6П.+ Вычислить интеграл: П/√2 + |
