Тест По Высшой Математике Для Дистанционников (Дьячков А. М.). Тест По Высшой Математике Для Дистанционников (Дьячков А. М. 1 1 e 1x e 1x ln x cos x2
 Скачать 481 Kb.
|
|
Расходиться, несуществует. + В силу предельного критерия сходимости несобственный интеграл 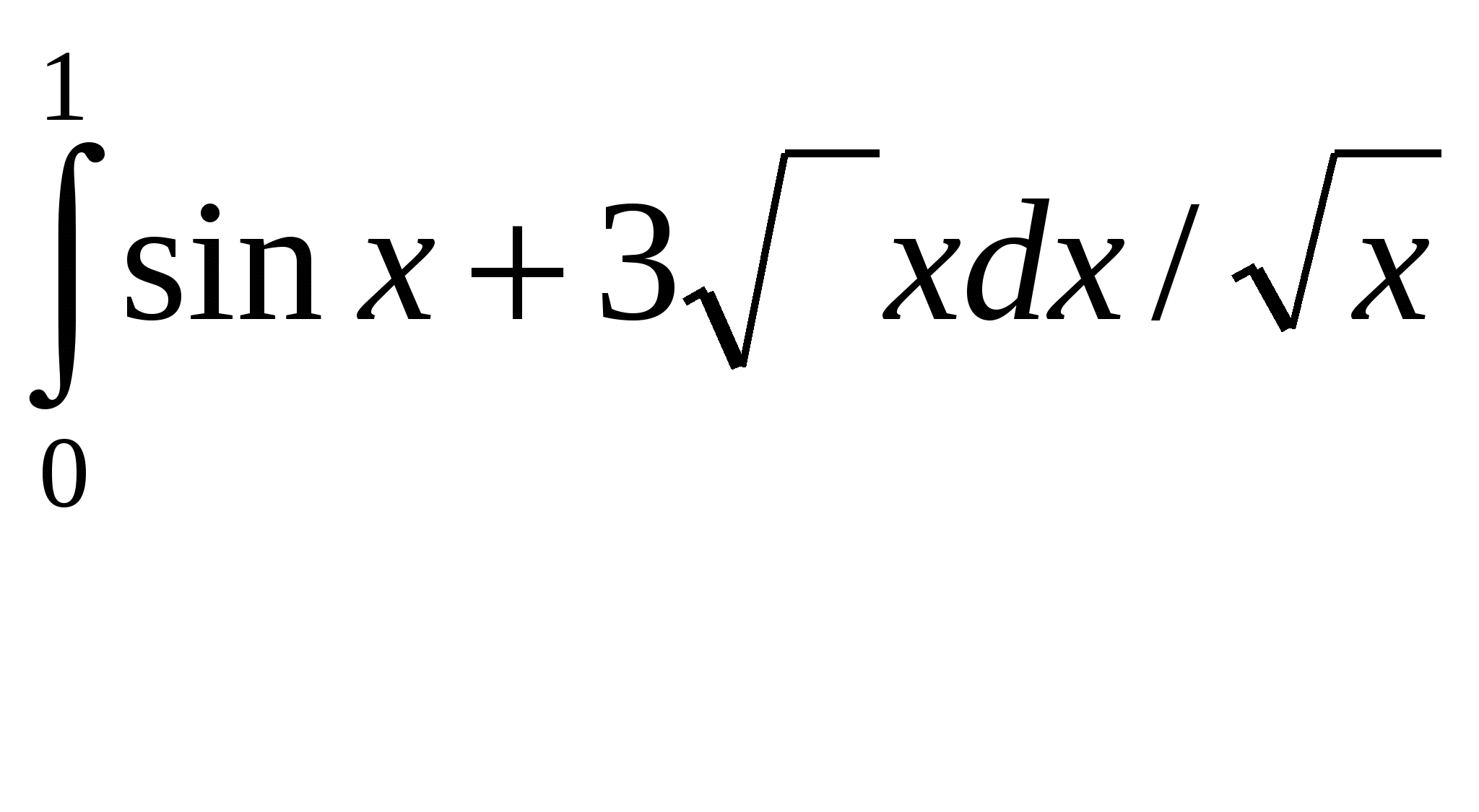 Сходиться, существует + В силу предельного критерия сходимости несобственный интеграл 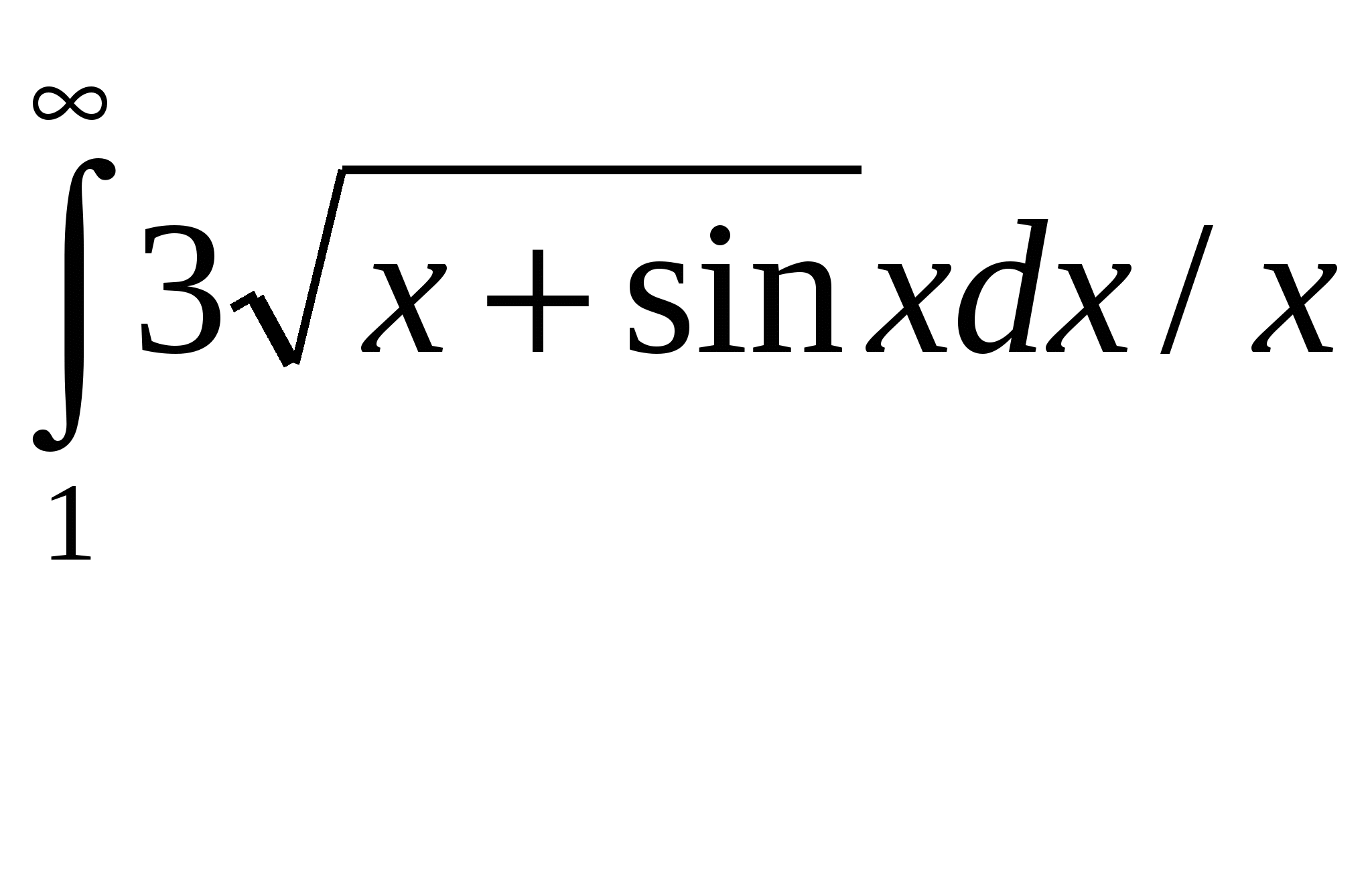  Расходиться, несуществует. + В силу предельного критерия сходимости несобственный интеграл 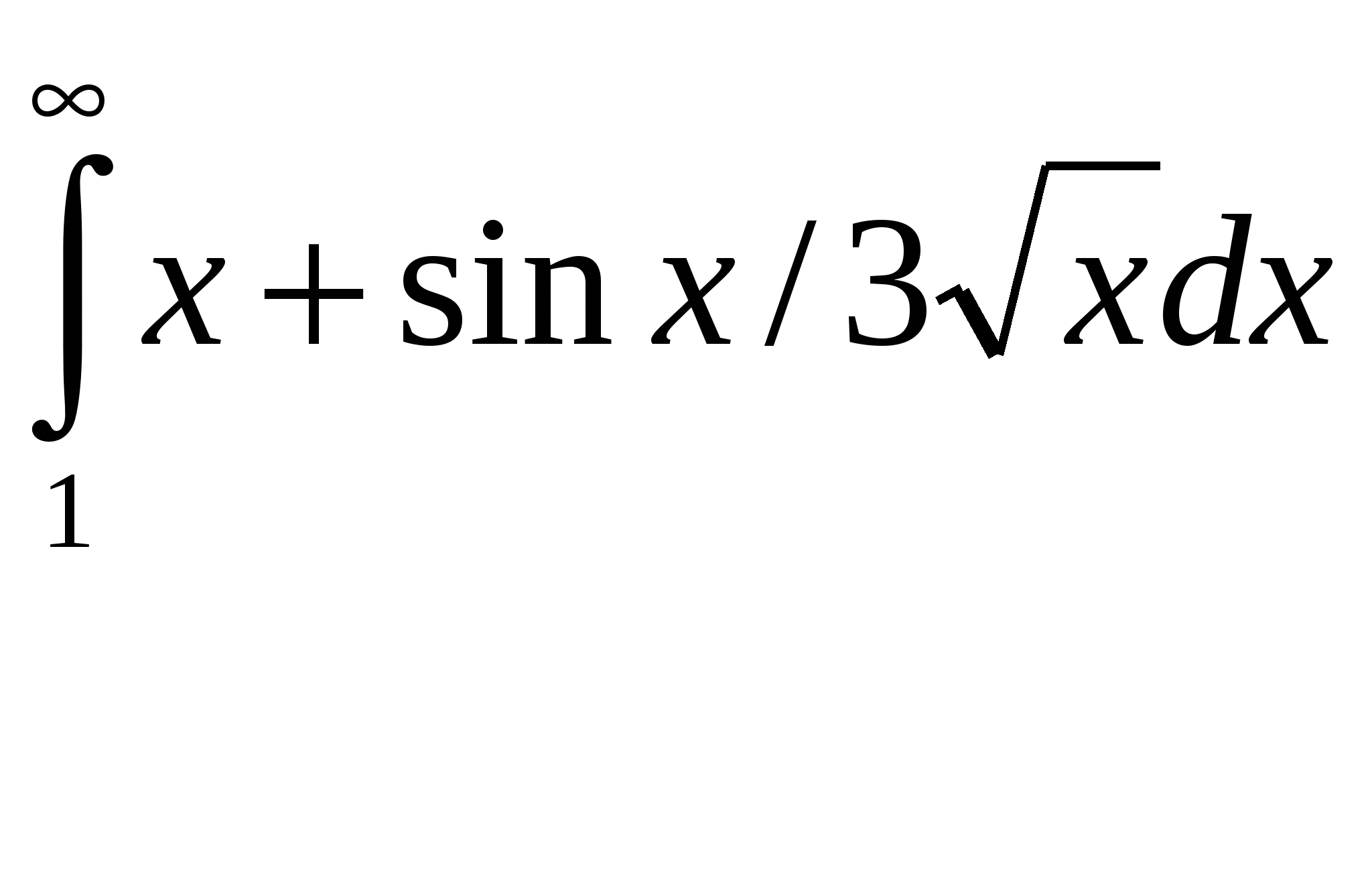 Расходиться, несуществует. + В силу предельного критерия сходимости несобственный интеграл 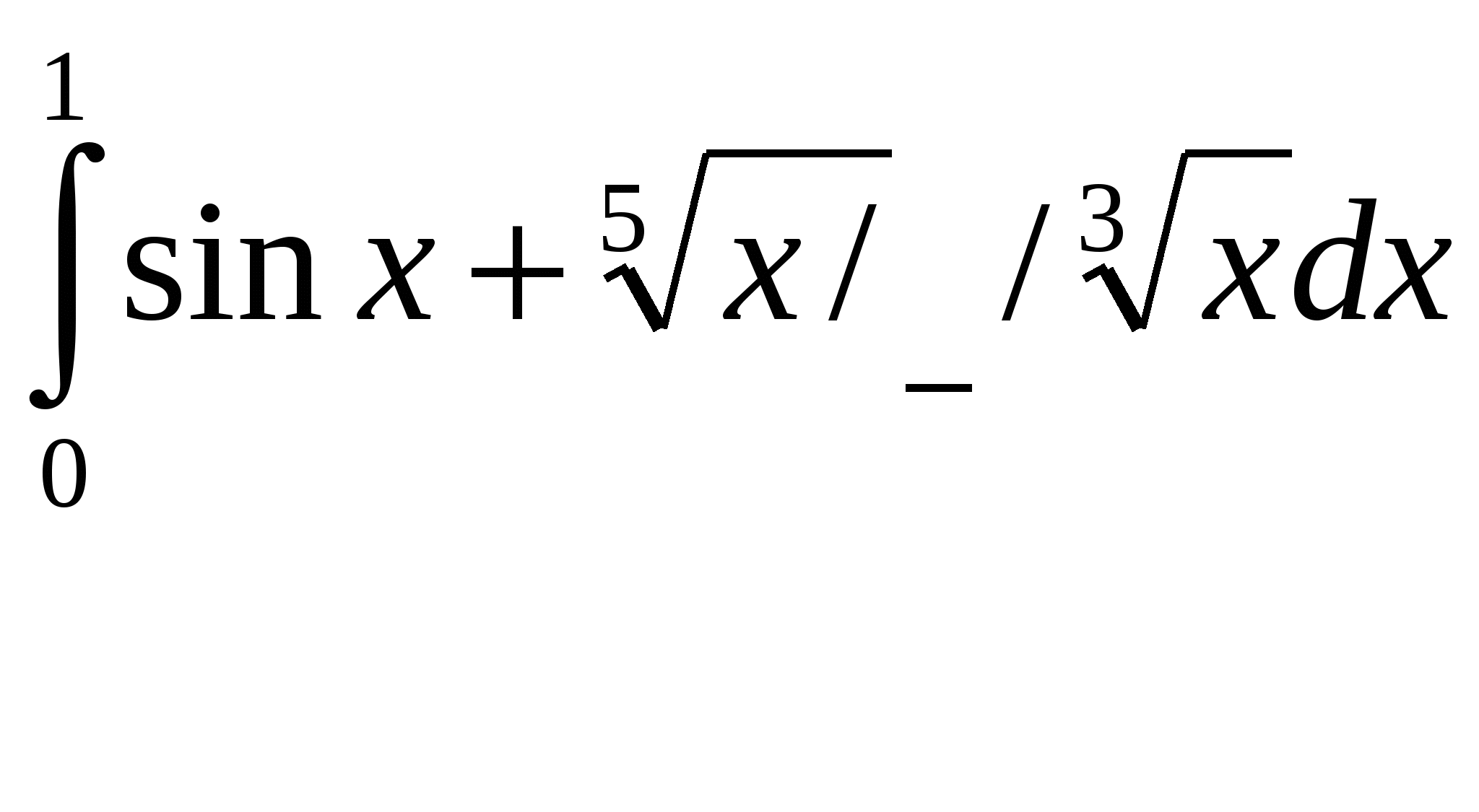 Сходиться, существует + В силу предельного критерия сходимости несобственный интеграл 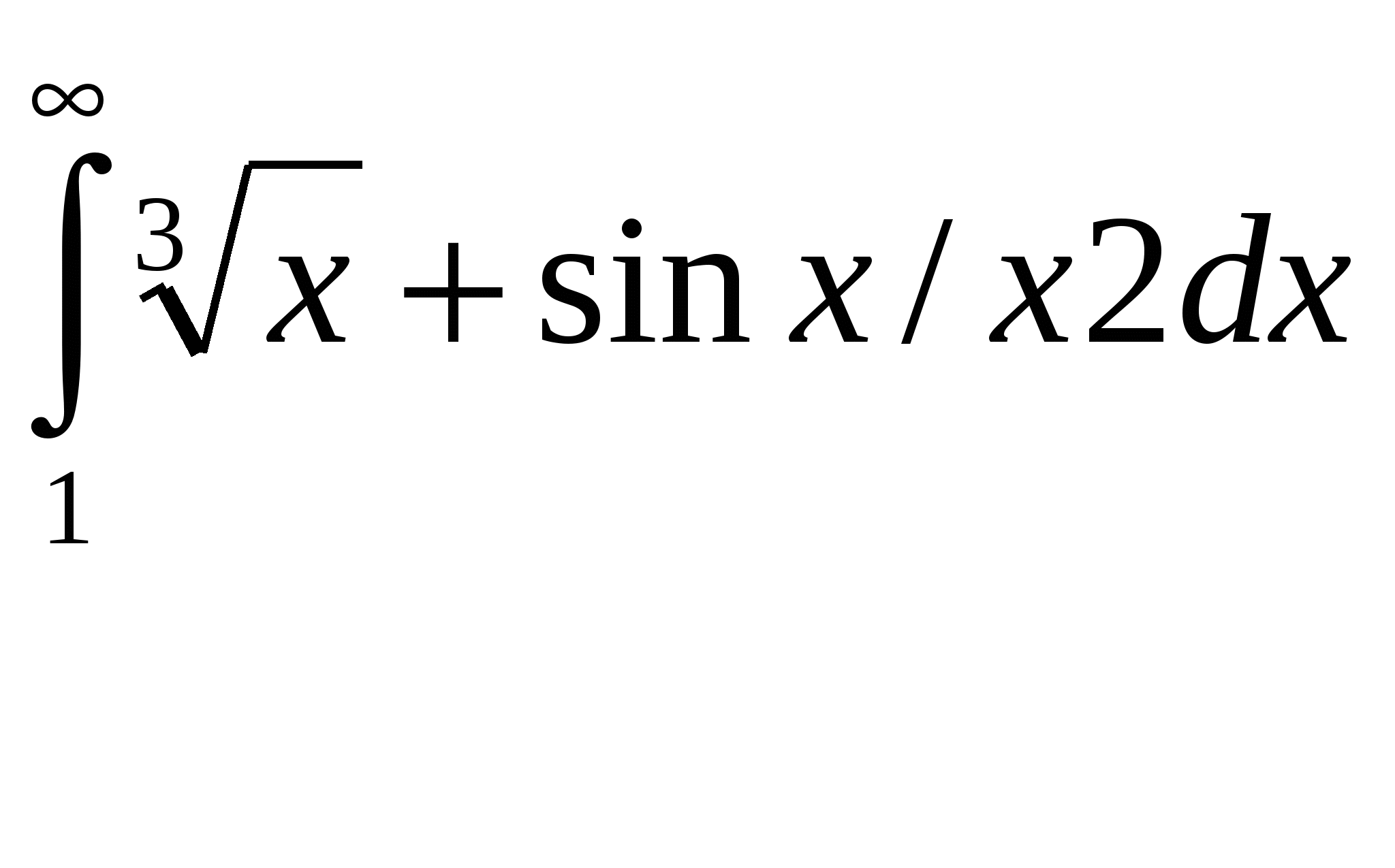 Сходиться, существует + В силу предельного критерия сходимости несобственный интеграл 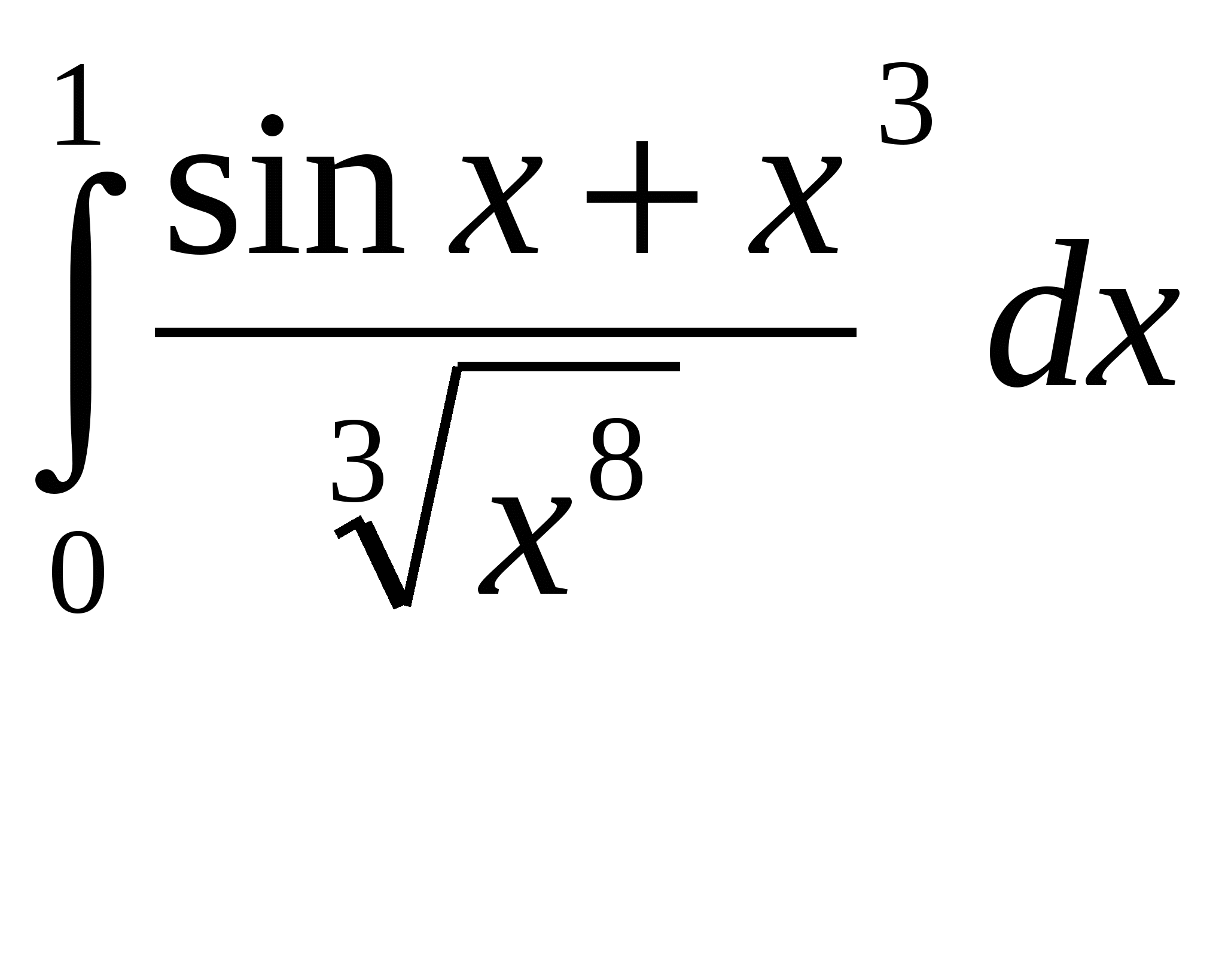 Расходиться, несуществует. + В силу предельного критерия сходимости несобственный интеграл 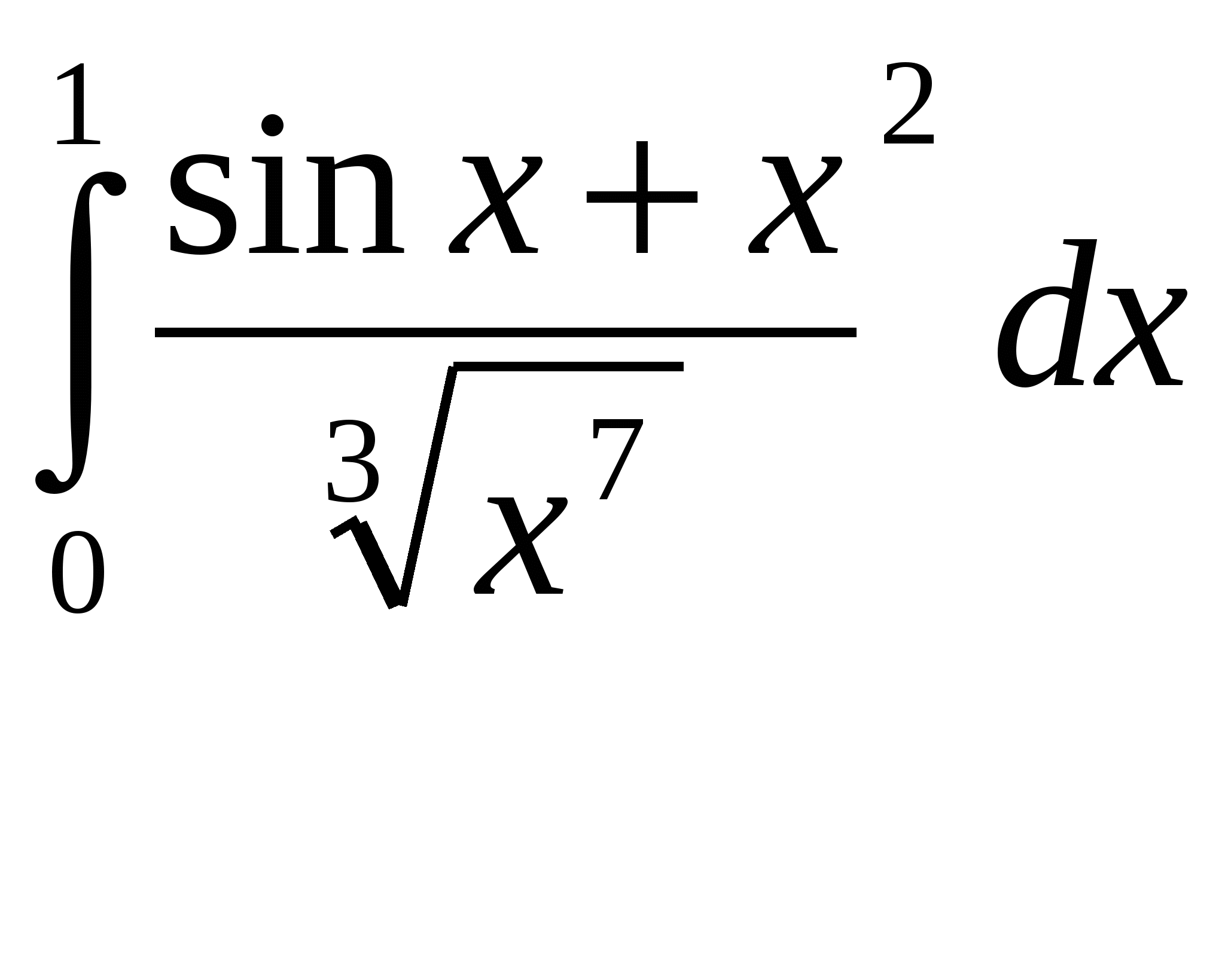 Расходиться, несуществует. + Необходимым условием интегрируемости функции на отрезке [a,b] является ее ограниченность на этом отрезке.+ Вертикальный шлюз имеет вид плоской фигуры, ограниченной параболой y=ax2 и прямой y=h. Чему равно давление воды на этот шлюз при a=4, h=9. 115,2 – нет, 51,2-нет. 66 2/3 нет Вертикальный шлюз имеет вид плоской фигуры, ограниченной параболой y=ax2 и прямой y=h. Чему равно давление воды на этот шлюз при a=1/5, h=5. 66 2/3 + Вертикальный шлюз имеет вид плоской фигуры, ограниченной параболой y=ax2 и прямой y=h. Чему равно давление воды на этот шлюз при a=1/6, h=6. 115,2 – нет, 51,2-нет, 64,8-нет, 65 1/3-нет Вертикальный шлюз имеет вид плоской фигуры, ограниченной параболой y=ax2 и прямой y=h. Чему равно давление воды на этот шлюз при a=1/9, h=4. 65 1/3-нет Вертикальный шлюз имеет вид равнобочной трапеции, нижнее основание которой равно 2а, верхнее -2b, а высота h. Чему равно давление воды на этот шлюз при a=5, b=8, h=5. 150+ Вертикальный шлюз имеет вид равнобочной трапеции, нижнее основание которой равно 2а, верхнее -2b, а высота h. Чему равно давление воды на этот шлюз при a=6, b=9, h=6. 150 – нет 225-нет Вертикальный шлюз имеет вид равнобочной трапеции, нижнее основание которой равно 2а, верхнее -2b, а высота h. Чему равно давление воды на этот шлюз при a=8, b=11, h=5. 225 + Вертикальный шлюз имеет вид равнобочной трапеции, нижнее основание которой равно 2а, верхнее -2b, а высота h. Чему равно давление воды на этот шлюз при a=7, b=10, h=6. 150 – нет, 252 нет 160 Не вычисляя полностью интеграл  , найти коэффициент k1 перед слагаемым k1ln│2x-1│в первообразной этого интеграла при а1=6, а2=6. 1,5 +Не вычисляя полностью интеграл , найти коэффициент k1 перед слагаемым k1ln│3x-1│в первообразной этого интеграла при а1=6, а2=-4. 1. ДаНе вычисляя полностью интеграл , найти коэффициент k1 перед слагаемым k1ln│3x-1│в первообразной этого интеграла при а1=9, а2=4. 1,5 +Не вычисляя полностью интеграл , найти коэффициент k1 перед слагаемым k1ln│3x-1│в первообразной этого интеграла при а1=3, а2=3. 1. Нет 1,5-нетНе вычисляя полностью интеграл , найти коэффициент k1 перед слагаемым k1ln│2x+1│в первообразной этого интеграла при а1=9, а2=4. 1,5. нетНе вычисляя полностью интеграл , найти коэффициент k1 перед слагаемым k1ln│3x+1│в первообразной этого интеграла при а1=6, а2=1. 0,5 +Не вычисляя полностью интеграл , найти коэффициент k1 перед слагаемым k1ln│2x-1│в первообразной этого интеграла при а1=8, а2=3. 1 Да.Не вычисляя полностью интеграл , найти коэффициент k1 перед слагаемым k1ln│2x+1│в первообразной этого интеграла при а1=8, а2=3. – 1 Да.Кривая y= e –ax sin wx (x ≥0, a ›0) вращается вокруг оси х. Чему равен объем полученного тела вращения при a =1, w =3. 2П/40+ Кривая y= e –ax sin wx (x ≥0, a ›0) вращается вокруг оси х. Чему равен объем полученного тела вращения при a =2, w =4. П/8 Кривая y= e –ax sin wx (x ≥0, a ›0) вращается вокруг оси х. Чему равен объем полученного тела вращения при a =1, w =√6/3. П/10 + Кривая y= e –ax sin wx (x ≥0, a ›0) вращается вокруг оси х. Чему равен объем полученного тела вращения при a =1, w =1. П/8.+ Кривая y= e –ax sin wx (x ≥0, a ›0) вращается вокруг оси х. Чему равен объем полученного тела вращения при a =1, w =2. П/5.+ Кривая y= e –ax sin wx (x ≥0, a ›0) вращается вокруг оси х. Чему равен объем полученного тела вращения при a =1, w =2√2. П/10 Кривая y= e –ax sin wx (x ≥0, a ›0) вращается вокруг оси х. Чему равен объем полученного тела вращения при a =2, w =2√2. П/10 нет 2П√40 – ytn, П/8-нет Кривая y= e –ax sin wx (x ≥0, a ›0) вращается вокруг оси х. Чему равен объем полученного тела вращения при a =1/2, w =√3/6. П/12 нет П/5-нет Кривая y= e –ax sin wx (x ≥0, a ›0) вращается вокруг оси х. Чему равен объем полученного тела вращения при a =1/2, w =√5/10. П/5 нет П/8 нет, П/10 нет Кривая y= e –ax sin wx (x ≥0, a ›0) вращается вокруг оси х. Чему равен объем полученного тела вращения при a =1, w =√6/3. П/20 Функция, имеющая в каждой точке интервала (а,b) производную, является Пусть f(x)-дифференцируемая функция такая, что  ,  . Найти значение функции f(a) при a=1, b=3, с=5. 8.+Пусть f(x)-дифференцируемая функция такая, что , . Найти значение функции f(a) при a=2, b=1, с=7. 4.+Пусть f(x)-дифференцируемая функция такая, что , . Найти значение функции f(a) при a=3, b=1, с=5. 2.+Пусть f(x)-дифференцируемая функция такая, что , . Найти значение функции f(a) при a=4, b=2, с=6. 2.+Пусть f(x)-дифференцируемая функция такая, что , . Найти значение функции f(a) при a=2, b=12, с=3. 3.Пусть f(x)-дифференцируемая функция такая, что , . Найти значение функции f(a) при a=-1, b=3, с=-5. 2. +Пусть f(x)-дифференцируемая функция такая, что , . Найти значение функции f(a) при a=-2, b=1, с=-7. 3.+Пусть f(x)-дифференцируемая функция такая, что , . Найти значение функции f(a) при a=-3, b=1, с=-7. 2. +Пусть f(x)-дифференцируемая функция такая, что , . Найти значение функции f(a) при a=5, b=12, с=3. 3. +Пусть f(x)-дифференцируемая функция такая, что , . Найти значение функции f(a) при a=1, b=3, с=5. 2. нетМногочлен Р5(х) = x5+5x4-4x3+2x2+a1x+a2 делится на двучлен (х-а3). a1 = 45, a2= 4, a3= -2. Отметить среди приведенных чисел верные значения остатка и свободного члена. 2,-2 нет 1 и-1 нет, 1,2- нет Многочлен Р5(х) = x5+5x4-4x3+2x2+a1x+a2 делится на двучлен (х-а3). a1 = -4, a2= -1, a3= 1. Отметить среди приведенных чисел верные значения остатка и свободного члена. 2,-2нет , 2 и -1 нет, Многочлен Р5(х) = x5+5x4-4x3+2x2+a1x+a2 делится на двучлен (х-а3). a1 = -5, a2= 3, a3= 1. Отметить среди приведенных чисел верные значения остатка и свободного члена. 2 и -1 + Многочлен Р5(х) = x5+5x4-4x3+2x2+a1x+a2 делится на двучлен (х-а3). a1 = 8, a2= -2, a3= -1. Отметить среди приведенных чисел верные значения остатка и свободного члена. 2 и 1 -нет , 0,1- нет, -1 и 2 нет, 0,2-нет, -2 и 1 Многочлен Р5(х) = x5+5x4-4x3+2x2+a1x+a2 делится на двучлен (х-а3). a1 = 9, a2= 1, a3= -1. Отметить среди приведенных чисел верные значения остатка и свободного члена. -1 и 2+ Многочлен Р5(х) = x5+5x4-4x3+2x2+a1x+a2 делится на двучлен (х-а3). a1 = -42, a2= -6, a3= 2. Отметить среди приведенных чисел верные значения остатка и свободного члена. -2 и 1 нет, -1 и 0- нет, -2 и 0 нет, -2 и 1-нет, -1 и 2нет Многочлен Р5(х) = x5+5x4-4x3+2x2+a1x+a2 делится на двучлен (х-а3). a1 = -43, a2= -2, a3= 2. Отметить среди приведенных чисел верные значения остатка и свободного члена. -1 и 0 нет -2 и 1 нет Многочлен Р5(х) = x5+5x4-4x3+2x2+a1x+a2 делится на двучлен (х-а3). a1 = 44, a2= -1, a3= -2. Отметить среди приведенных чисел верные значения остатка и свободного члена. 2 -2 нет 1-1 нет Есть ли в разложении многочлена Р4(х) = х4 – 3х3+х2+3х-2 на неприводимые сомножители сомножитель, равный (х-1)2? Да. + Есть ли в разложении многочлена Р4(х) = х4 – 3х3+3х2-3х-2 на неприводимые сомножители сомножитель, равный (х2+1)? Да. Есть ли в разложении многочлена Р4(х) = х4 – 3х3+3х2-3х+2 на неприводимые сомножители сомножитель, равный (х2+1)? Да.+ Есть ли в разложении многочлена Р4(х) = х4 – 3х3+3х2-2х-2 на неприводимые сомножители сомножитель, равный (х2+1)? Нет.+ Есть ли в разложении многочлена Р4(х) = х4 – х3-2х-4 на неприводимые сомножители сомножитель, равный (х2+2)? Да.+ Есть ли в разложении многочлена Р4(х) = х4 – х3-2х-2 на неприводимые сомножители сомножитель, равный (х2+2)? Нет.+ Есть ли в разложении многочлена Р4(х) = х4 – 3х3+х+2 на неприводимые сомножители сомножитель, равный (х+2)2? Да. Есть ли в разложении многочлена Р4(х) = х4 – 3х3+х2+2х-2 на неприводимые сомножители сомножитель, равный (х-1)2? Нет.+ Есть ли в разложении многочлена Р4(х) = х4 – 3х3-2х2+12х-8 на неприводимые сомножители сомножитель, равный (х-2)2? Да.+ Есть ли в разложении многочлена Р4(х) = х4 – х3-3х+2 на неприводимые сомножители сомножитель, равный (х2+2)? Да.+ Есть ли в разложении многочлена Р4(х) = х4 – х3 - 3х3+х+2 на неприводимые сомножители сомножитель, равный (х-1)2? Да.+ Достаточным условием интегрируемости функции на отрезке [a,b] является ее непрерывность на этом отрезке.+ Если предел  существует, то он называется Производной функции f(x) в точке x0. +Непрерывная функция, производная которой совпадает с функцией f(x) в точках непрерывности, называется первообразной функции f(x). Да. Две первообразные одной и той же функции отличаются друг от друга на Всякое бесконечное пронумерованное множество называется счетным.+ Множество точек числовой оси, удовлетворяющих неравенству x >ε (ε > 0 ), называется окрестностью бесконечно удаленной точки.+ Если левый и правый пределы функции f(x) в точке х0 равны, а функция не определена в точке х0, то она терпит устранимый разрыв в точке х0.+ Бесконечно малые в точке х0 функции а(х) и В(х) называются эквивалентными если lim a(x)/B(x)=1. Вставить пропущенное слово. Решить систему дифференциальных уравнений 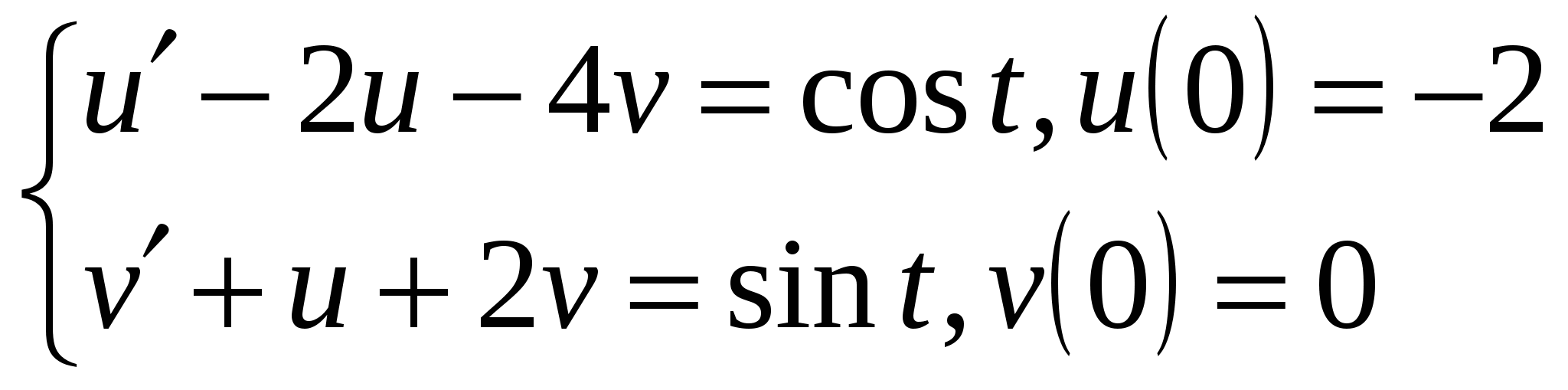 и = -(2cost + 3 sint) y = 2sint. + Решить систему дифференциальных уравнений 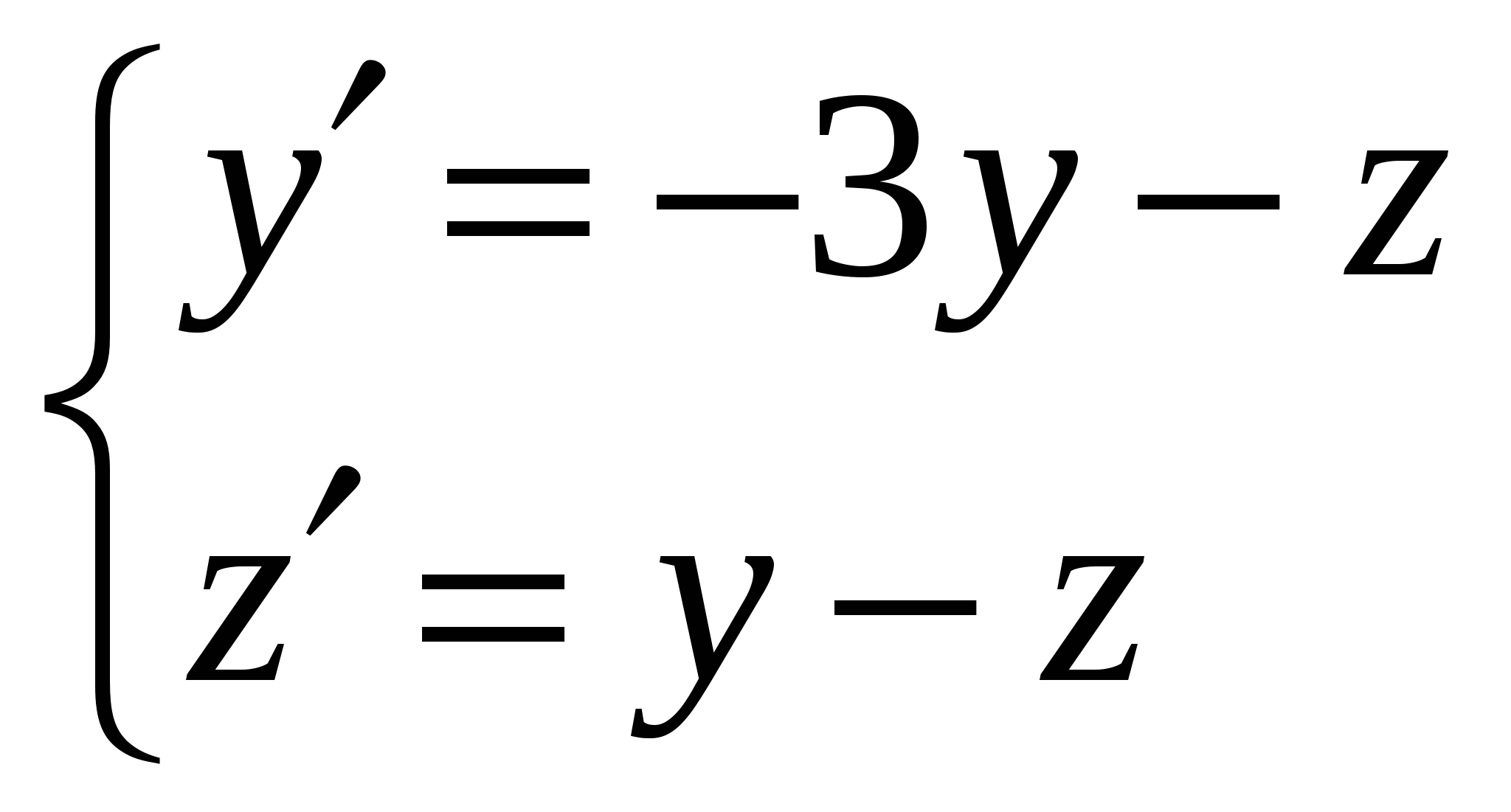 y = (c1 – c2 – c1x)e-2x Z = (c1x + c2)e-2x. + Решить систему дифференциальных уравнений 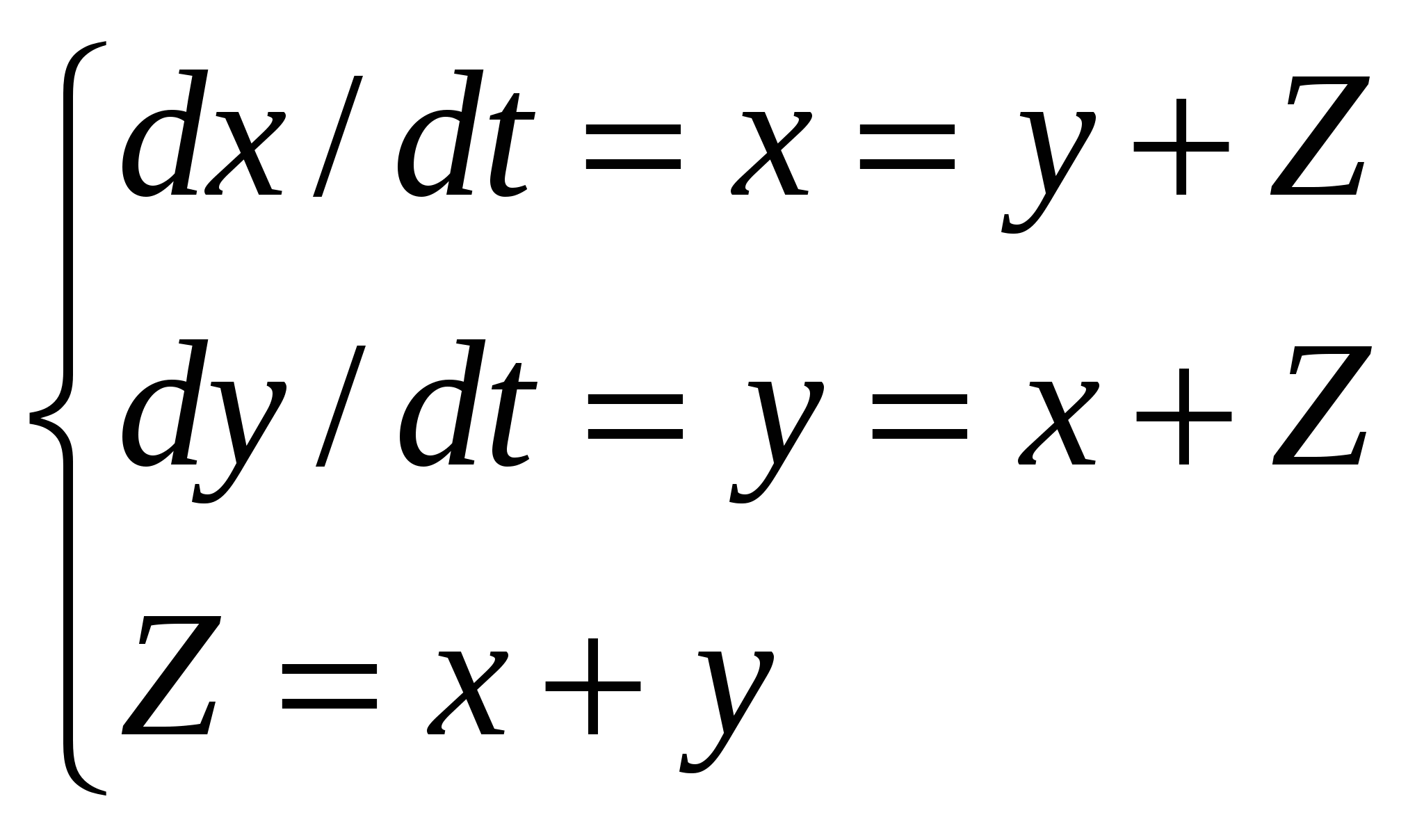 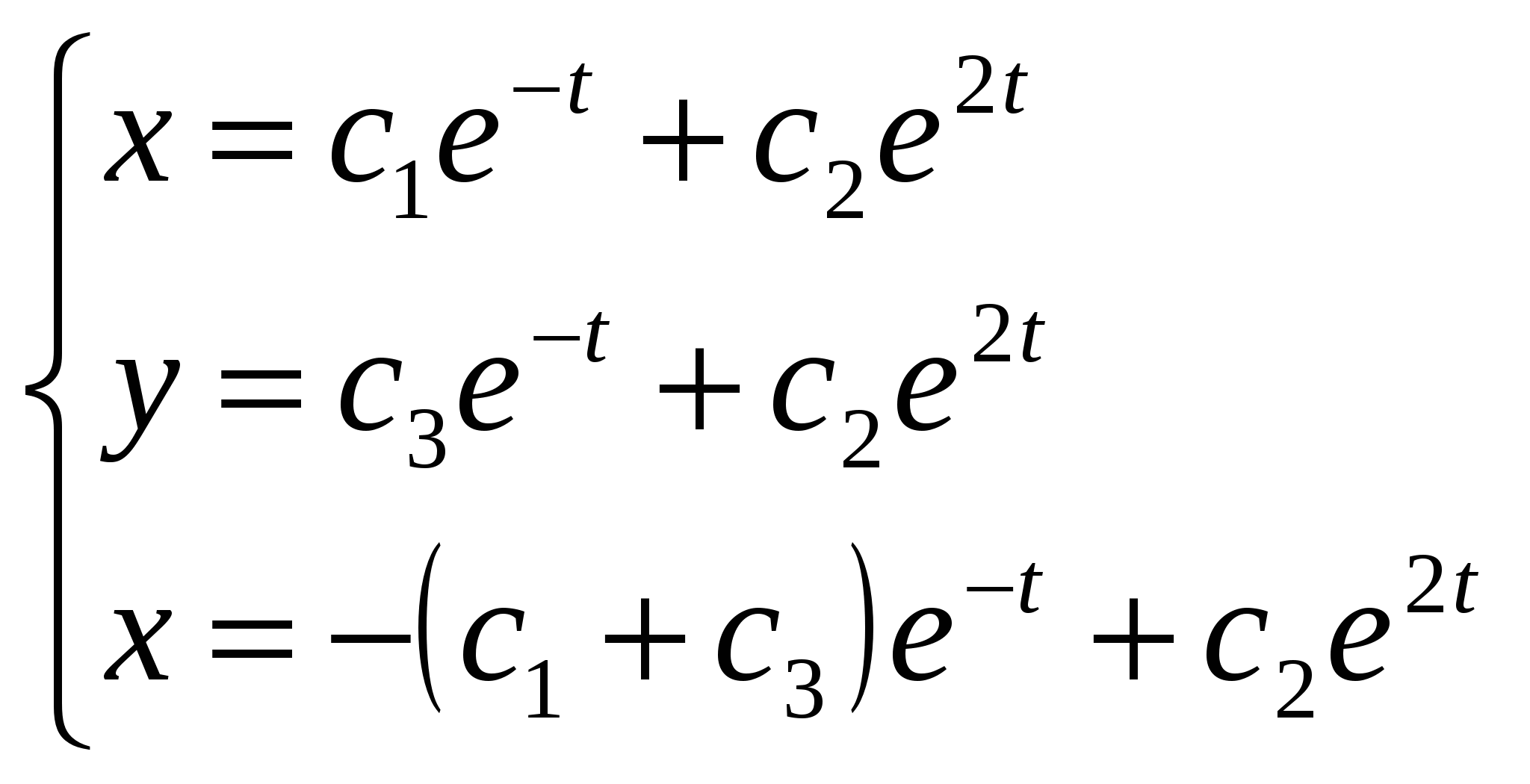 +Решить систему дифференциальных уравнений 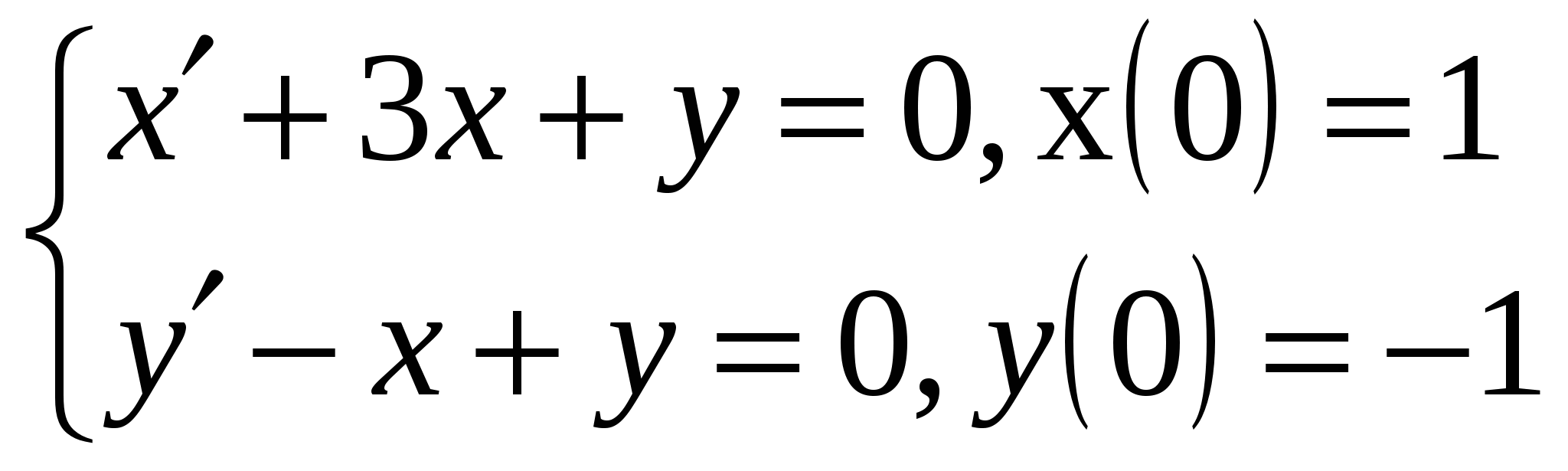 x = e-2t, + y = - e-2t. Решить систему дифференциальных уравнений 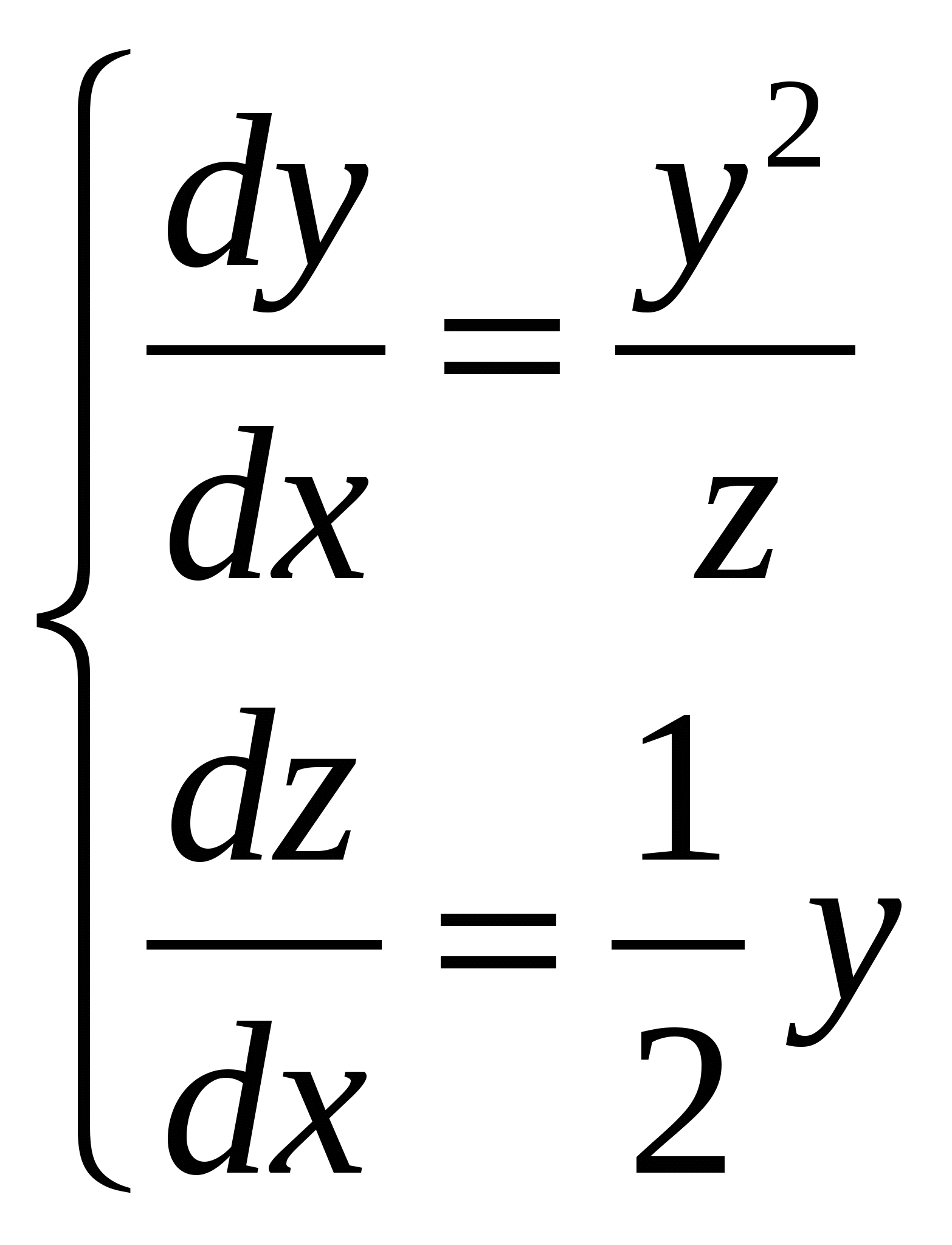 y = ____c1___, (c2 – x) Z = c2 – x. нет y = ____5c1___, (c2 – x)2 Z = c2 – x. нет Решить дифференциальные уравнение:  , ,  |