Тест По Высшой Математике Для Дистанционников (Дьячков А. М.). Тест По Высшой Математике Для Дистанционников (Дьячков А. М. 1 1 e 1x e 1x ln x cos x2
 Скачать 481 Kb. Скачать 481 Kb.
|
|
Выберите функции интегрируемые по Риману на отрезке [-1,1]. + 1___ 1 + e 1/x e -1/x ln │x│ cos x2 Выберите функции интегрируемые по Риману на отрезке [-1,1]. + 1 – cos2x___ x │x│ 1 ___ sinx e 1/x Выберите функции интегрируемые по Риману на отрезке [-1,1]. + 1__ │x│ sin x __1__ 3√x x___ arcsin x Выберите функции интегрируемые по Риману на отрезке [-1,1]. + │x│_ x ___x___ 2 - 1 __sin x__ x3 ctg x Выберите функции интегрируемые по Риману на отрезке [-1,1]. + x_ cos x ___1___ x2 +2x __1__ x2 tg x Выберите функции интегрируемые по Риману на отрезке [-1,1]. + 1__ cos x arctg 1 x e -2/│x│ Таких объектов нет 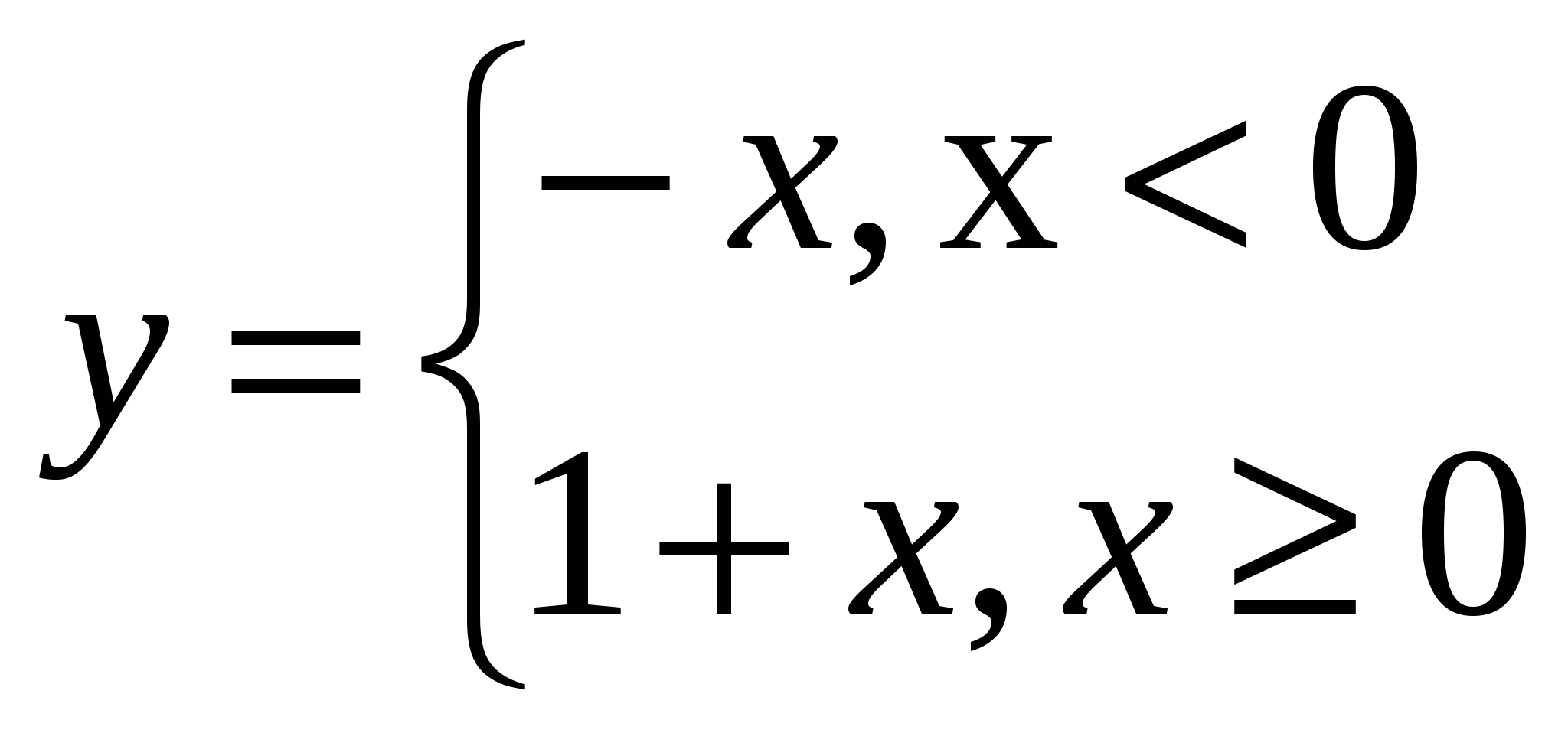 и + и +Выберите функции интегрируемые по Риману на отрезке [-1,1]. + 1_ √ x ___x___ sinx __2__ x2 -2x __arcsinx__ X Выберите функции интегрируемые по Риману на отрезке [-1,1]. + │x│_ x ___x___ 2 - 1 __sin x__ x3 ctg x Выберите функции интегрируемые по Риману на отрезке [-1,1]. нет 1_ x ___cosx___ x __sin x__ x ln x2 Выберите функции неинтегрируемые по Риману на отрезке [-1,1]. + 1_ x ___cosx___ x __sin x__ x ln x2 Выберите функции неинтегрируемые по Риману на отрезке [-1,1]. + │x│_ x ___x___ 2 - 1 __sin x__ x3 ctg x Выберите функции неинтегрируемые по Риману на отрезке [-1,1]. ytn 1_ x ___cosx___ x __sin x__ x ln x2 Выберите функции неинтегрируемые по Риману на отрезке [-1,1]. + 1_ √ x ___x___ sinx __2__ x2 -2x __arcsinx__ X Выберите функции неинтегрируемые по Риману на отрезке [-1,1]. + 1__ │x│ sin x __1__ 3√x x___ arcsin x Выберите функции неинтегрируемые по Риману на отрезке [-1,1]. + x_ cos x ___1___ x2 +2x __1__ x2 tg x Выберите функции интегрируемые по Риману на отрезке [-1,1]. + 1___ 1 + e 1/x e -1/x ln │x│ cos x2 При каком значении константы C первообразная интеграла ⌠ ____dx___ =F(x)+C, x0=0 4√(16-3x)3 обращается в нуль? 8/3.+ При каком значении константы C первообразная интеграла При каком значении константы C первообразная интеграла При каком значении константы C первообразная интеграла При каком значении константы C первообразная интеграла При каком значении константы C первообразная интеграла При каком значении константы C первообразная интеграла При каком значении константы C первообразная интеграла Точка движется по прямой с ускорением ϖ(t) = cos2t. Начальная скорость V0=2 . Тогда скорость точки в момент времени t1= П/12 равна: 9/4.+ Точка движется по прямой с ускорением ϖ(t) = Точка движется по прямой с ускорением ϖ(t) = sin2t. Начальная скорость V0=2 . Тогда скорость точки в момент времени t1= П/4 равна: 5/2 . + Точка движется по прямой с ускорением ϖ(t) = cos2t. Начальная скорость V0=2 . Тогда скорость точки в момент времени t1= П/4 равна: 5/2 .+ Точка движется по прямой с ускорением ϖ(t) = sin2t. Начальная скорость V0=2 . Тогда скорость точки в момент времени t1= П/6 равна: 9/4.+ Точка движется по прямой с ускорением ϖ(t) = Точка движется по прямой с ускорением Точка движется по прямой с ускорением ϖ(t) = Если функция f(x) интегрируема на отрезке [a,b], то функция = F(x) ∫ f (t)dt (a ≤ x ≤ b) является непрерывной на отрезке [a,b]. Главное значение несобственного интеграла Главное значение несобственного интеграла Главное значение несобственного интеграла Главное значение несобственного интеграла Главное значение несобственного интеграла Главное значение несобственного интеграла Главное значение несобственного интеграла Главное значение несобственного интеграла Дан интеграл Дан интеграл Дан интеграл Дан интеграл Дан интеграл Дан интеграл Дан интеграл Дан интеграл Дан интеграл Указать подстановку, которая рационализирует подынтегральное выражение интеграла ∫ ___dx____ т.е. подынтегральное выражение становиться рациональной функцией √x + 83 √x2 Новой переменной t. Указать подстановку, которая рационализирует подынтегральное выражение интеграла ∫ ___dx____ т.е. подынтегральное выражение становиться рациональной функцией √x + 6 √x5 Новой переменной t. Указать подстановку, которая рационализирует подынтегральное выражение интеграла ∫ ___dx____ т.е. подынтегральное выражение становиться рациональной функцией √x +4 4 √x3 Новой переменной t. Указать подстановку, которая рационализирует подынтегральное выражение интеграла ∫ ___dx____ т.е. подынтегральное выражение становиться рациональной функцией √x +2 5 √x4 Новой переменной t. Указать подстановку, которая рационализирует подынтегральное выражение интеграла ∫ ___dx____ т.е. подынтегральное выражение становиться рациональной функцией 3√x +√x3 Новой переменной t. Указать подстановку, которая рационализирует подынтегральное выражение интеграла ∫ ___dx____ т.е. подынтегральное выражение становиться рациональной функцией 3√x -√x3 Новой переменной t. Указать подстановку, которая рационализирует подынтегральное выражение интеграла ∫ ___dx____ т.е. подынтегральное выражение становиться рациональной функцией 3√x -3√x2 Новой переменной t. Указать подстановку, которая рационализирует подынтегральное выражение интеграла ∫ ___dx____ т.е. подынтегральное выражение становиться рациональной функцией 3√x -4√x3 Новой переменной t. Является ли интеграл ∫ xm (a + bxn )p dx неберущимся, т.е. будет ли его первообразная функцией неэлементарной при m = 2/3, n = 3, p = 1/7. Да.+ Является ли интеграл ∫ xm (a + bxn )p dx неберущимся, т.е. будет ли его первообразная функцией неэлементарной при m = 6, n = 1/3, p = 1/2. Нет. Является ли интеграл ∫ xm (a + bxn )p dx неберущимся, т.е. будет ли его первообразная функцией неэлементарной при m = 1/2, n = 2, p = 1/3. Да.+ Является ли интеграл ∫ xm (a + bxn )p dx неберущимся, т.е. будет ли его первообразная функцией неэлементарной при m = 1/3, n = 3, p = 1/4. Да.+ Является ли интеграл ∫ xm (a + bxn )p dx неберущимся, т.е. будет ли его первообразная функцией неэлементарной при m = 3/5, n = 2, p = 1/5. Нет.+ Является ли интеграл ∫ xm (a + bxn )p dx неберущимся, т.е. будет ли его первообразная функцией неэлементарной при m = 1/2, n = 4, p = 1/6. Да.+ Является ли интеграл ∫ xm (a + bxn )p dx неберущимся, т.е. будет ли его первообразная функцией неэлементарной при m = 5/2, n = 4, p = 1/8. Нет. Является ли интеграл ∫ xm (a + bxn )p dx неберущимся, т.е. будет ли его первообразная функцией неэлементарной при m = 2, n = 5, p = 1/9. Да.+ Если разложить рациональную дробь a1x + a2 , на простейшие дроби, то значения (x-1)3(x-2)2(x-3) коэффициентов k1 и k2 при простейших дробях _k1_ и _k2_ будут среди следующих значений x-3 (x-2)2 чисел (a1 = -22, a2 = 42): 2 и -2 нет 1, -1 нет -3 и -1 нет. 1,2 нет -3,2 Если разложить рациональную дробь a1x + a2 , на простейшие дроби, то значения (x-1)3(x-2)2(x-3) коэффициентов k1 и k2 при простейших дробях _k1_ и _k2_ будут среди следующих значений x-3 (x-2)2 чисел (a1 = 14, a2 = -26): 2 и -2 да Если разложить рациональную дробь a1x + a2 , на простейшие дроби, то значения (x-1)3(x-2)2(x-3) коэффициентов k1 и k2 при простейших дробях _k1_ и _k2_ будут среди следующих значений x-3 (x-2)2 чисел (a1 = -2, a2 = -2): 1 и -1 нет 2,-2-нет, 2 и -3 –нет, 1,2-нет Если разложить рациональную дробь a1x + a2 , на простейшие дроби, то значения (x-1)3(x-2)2(x-3) коэффициентов k1 и k2 при простейших дробях _k1_ и _k2_ будут среди следующих значений x-3 (x-2)2 чисел (a1 = 5, a2 = 1): 1 и -1 нет , -1 и 2 –нет, -3 и 1нет Если разложить рациональную дробь a1x + a2 , на простейшие дроби, то значения (x-1)3(x-2)2(x-3) коэффициентов k1 и k2 при простейших дробях _k1_ и _k2_ будут среди следующих значений x-3 (x-2)2 чисел (a1 = -15, a2 = 29): 1 и -1 нет , 1 -3нет , -2 и 1 Если разложить рациональную дробь a1x + a2 , на простейшие дроби, то значения (x-1)3(x-2)2(x-3) коэффициентов k1 и k2 при простейших дробях _k1_ и _k2_ будут среди следующих значений x-3 (x-2)2 чисел (a1 = 5, a2 = -7): 1 и -3 да Если разложить рациональную дробь a1x + a2 , на простейшие дроби, то значения (x-1)3(x-2)2(x-3) коэффициентов k1 и k2 при простейших дробях _k1_ и _k2_ будут среди следующих значений x-3 (x-2)2 чисел (a1 = 1, a2 = 5): -3 и 1 да Чему равна площадь фигуры, ограниченной прямой y = kx и параболой y = ax2 +bx при k =4, a= -1, b = -2. 36.+ Чему равна площадь фигуры, ограниченной прямой y = kx и параболой y = ax2 +bx при k =4, a= 1, b = 1. 4,5 + Чему равна площадь фигуры, ограниченной прямой y = kx и параболой y = ax2 +bx при k =7, a= 1, b = 1. 36. Чему равна площадь фигуры, ограниченной прямой y = kx и параболой y = ax2 +bx при k =7, a= 2, b = 1. 9. + Чему равна площадь фигуры, ограниченной прямой y = kx и параболой y = ax2 +bx при k =8, a= 2, b = 2. 9. + Чему равна площадь фигуры, ограниченной прямой y = kx и параболой y = ax2 +bx при k =2, a= -1, b = -1. 9. Чему равна площадь фигуры, ограниченной прямой y = kx и параболой y = ax2 +bx при k =1, a= -2, b = 7. 9. + Чему равна площадь фигуры, ограниченной прямой y = kx и параболой y = ax2 +bx при k =-1, a= -1, b = 5. 36. + Две точки стартуют одновременно из начала координат в момент времени t0=0 и движутся вдоль оси x со скоростями v1 = a1t2 + b1t и v2 = a2t2 + b2t при a1 = 2, b1 = 5, a2 = 5, b2 = 1 соответственно. Отставая в начале движения, вторая точка догоняет первую в момент времени t1 равный: 2. + Две точки стартуют одновременно из начала координат в момент времени t0=0 и движутся вдоль оси x со скоростями v1 = a1t2 + b1t и v2 = a2t2 + b2t при a1 = 1, b1 = 6, a2 = 4, b2 = 4 соответственно. Отставая в начале движения, вторая точка догоняет первую в момент времени t1 равный: 1. + Две точки стартуют одновременно из начала координат в момент времени t0=0 и движутся вдоль оси x со скоростями v1 = a1t2 + b1t и v2 = a2t2 + b2t при a1 = 1, b1 = 6, a2 = 7, b2 = 2 соответственно. Отставая в начале движения, вторая точка догоняет первую в момент времени t1 равный: 1. + Две точки стартуют одновременно из начала координат в момент времени t0=0 и движутся вдоль оси x со скоростями v1 = a1t2 + b1t и v2 = a2t2 + b2t при a1 = 2, b1 = 5, a2 = 8, b2 = 3 соответственно. Отставая в начале движения, вторая точка догоняет первую в момент времени t1 равный: 0,5. + Две точки стартуют одновременно из начала координат в момент времени t0=0 и движутся вдоль оси x со скоростями v1 = a1t2 + b1t и v2 = a2t2 + b2t при a1 = 7, b1 = 3, a2 = 1, b2 = 5 соответственно. Отставая в начале движения, вторая точка догоняет первую в момент времени t1 равный: 0,5. нет Две точки стартуют одновременно из начала координат в момент времени t0=0 и движутся вдоль оси x со скоростями v1 = a1t2 + b1t и v2 = a2t2 + b2t при a1 = 5, b1 = 1, a2 = 2, b2 = 5 соответственно. Отставая в начале движения, вторая точка догоняет первую в момент времени t1 равный: 2. Две точки стартуют одновременно из начала координат в момент времени t0=0 и движутся вдоль оси x со скоростями v1 = a1t2 + b1t и v2 = a2t2 + b2t при a1 = 6, b1 = 4, a2 = 3, b2 = 7 соответственно. Отставая в начале движения, вторая точка догоняет первую в момент времени t1 равный: 1,5. + Две точки стартуют одновременно из начала координат в момент времени t0=0 и движутся вдоль оси x со скоростями v1 = a1t2 + b1t и v2 = a2t2 + b2t при a1 = 3, b1 = 1, a2 = 2, b2 = 3 соответственно. Отставая в начале движения, вторая точка догоняет первую в момент времени t1 равный: 3. + Чему равна площадь одного лепестка кривой r = a sin (wф) при a = 4√5, w=5. 4П. + Чему равна площадь одного лепестка кривой r = a sin (wф) при a = 4, w=2. 2П. + Чему равна площадь одного лепестка кривой r = a sin (wф) при a = 6, w=3. 3П. + Чему равна площадь одного лепестка кривой r = a sin (wф) при a = 4, w=4. П. + Чему равна площадь одного лепестка кривой r = a sin (wф) при a = 6√2, w=6. 3П. + Чему равна площадь одного лепестка кривой r = a sin (wф) при a = 2√35, w=7. 5П. + Чему равна площадь одного лепестка кривой r = a sin (wф) при a = 8, w=8. 2П. + Чему равна площадь одного лепестка кривой r = a sin (wф) при a = 6, w=9. П. + Прямая х=х0 называется вертикальной асимптотой, если lim f(x) = ∞ + x-x0 Сопоставить интегралы, стоящие в левом столбце, и числа правого столбца: + 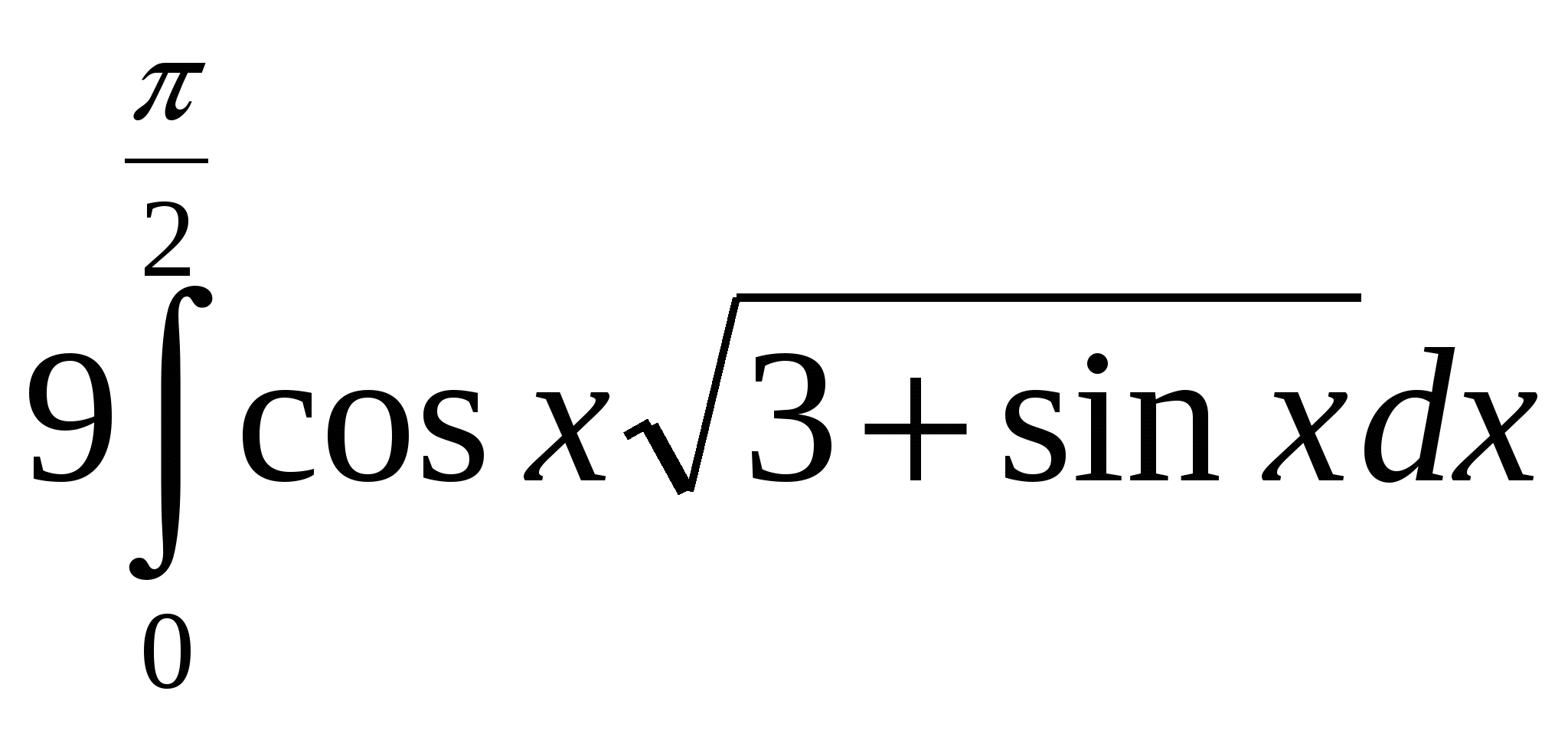 30 30Сопоставить интегралы+ Сопоставить интегралы+ 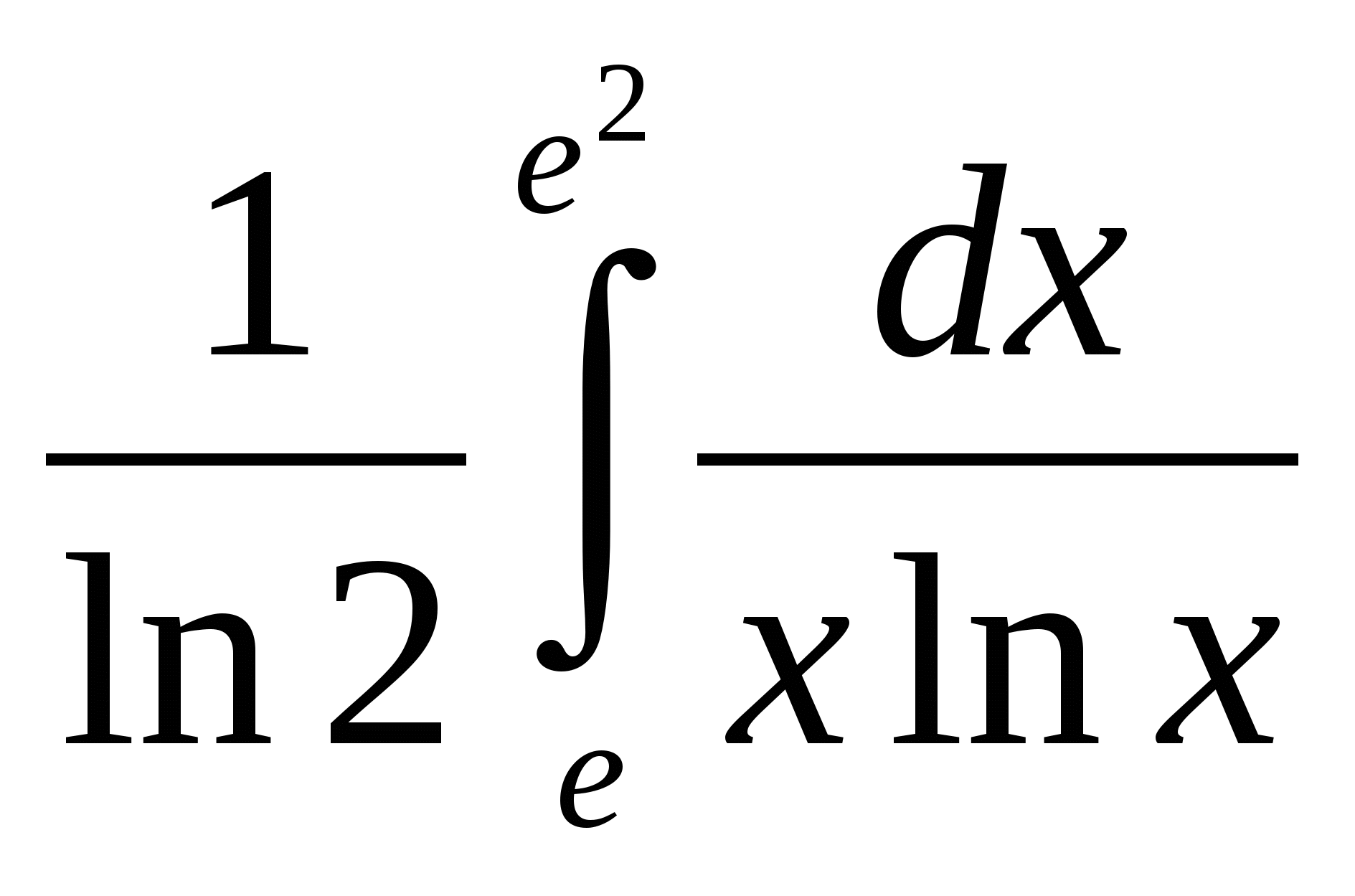 1 1Сопоставить интегралы + Сопоставить интегралы + 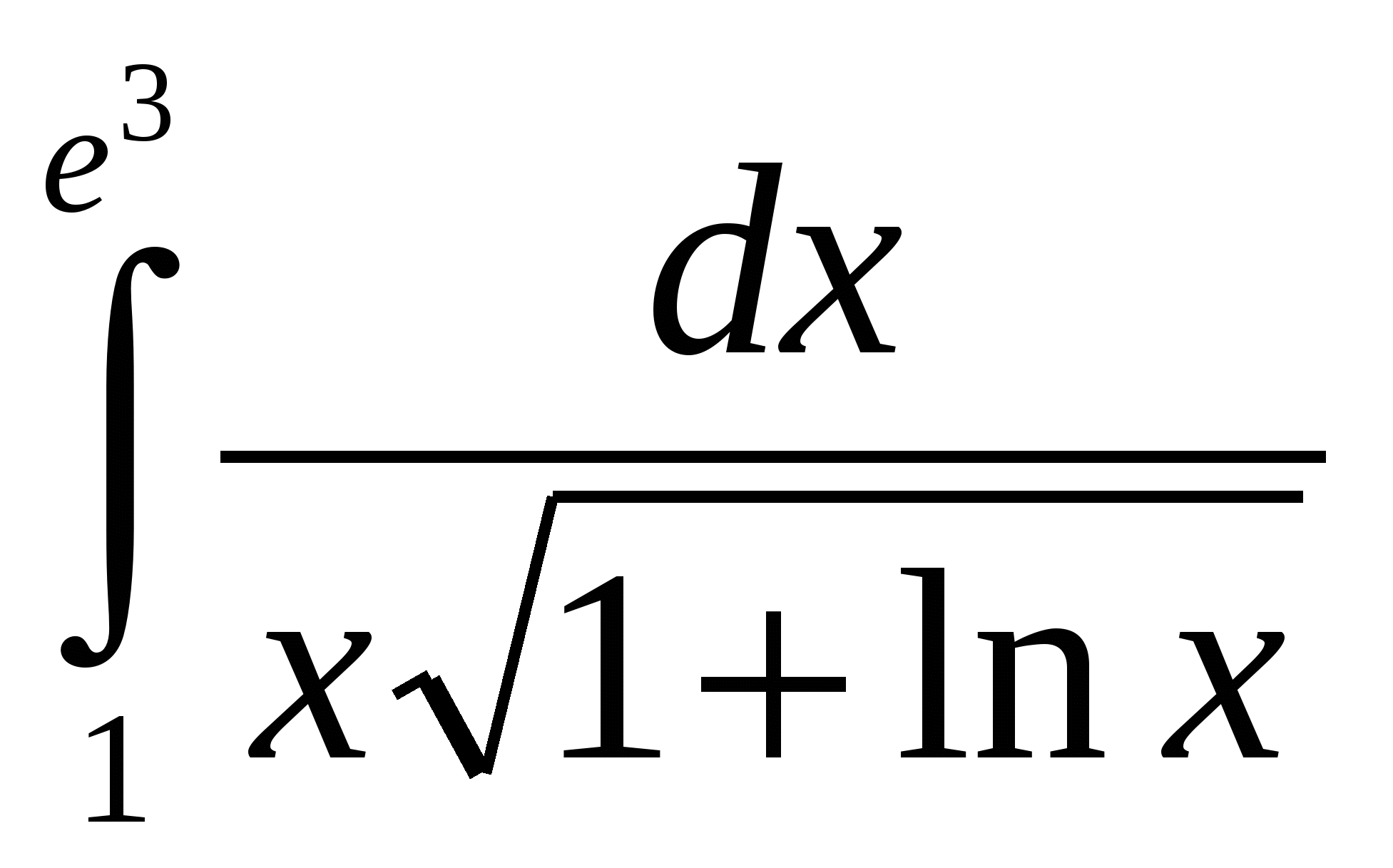 2 2Сопоставить интегралы + Сопоставить интегралы + 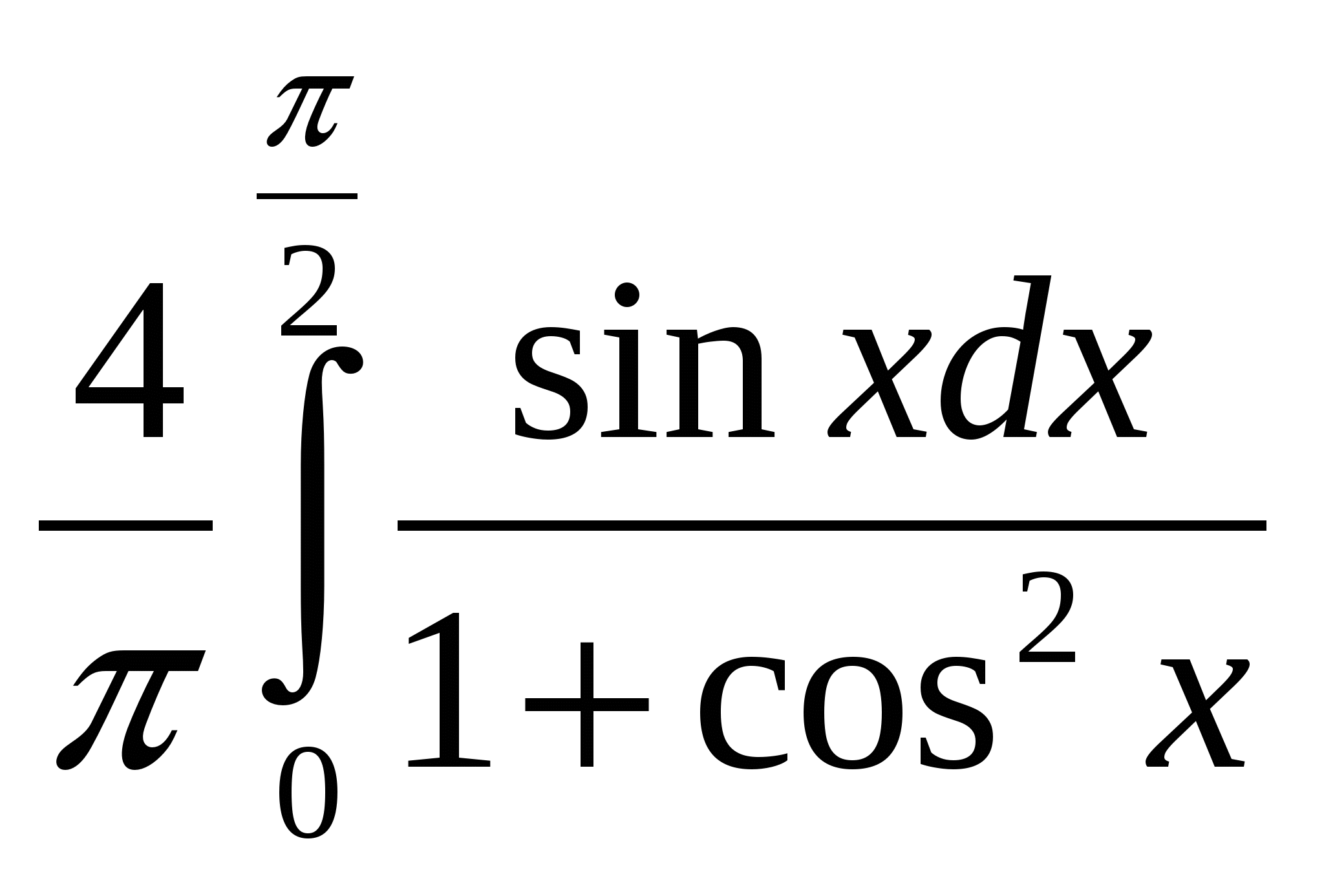 1 1Сопоставить интегралы + 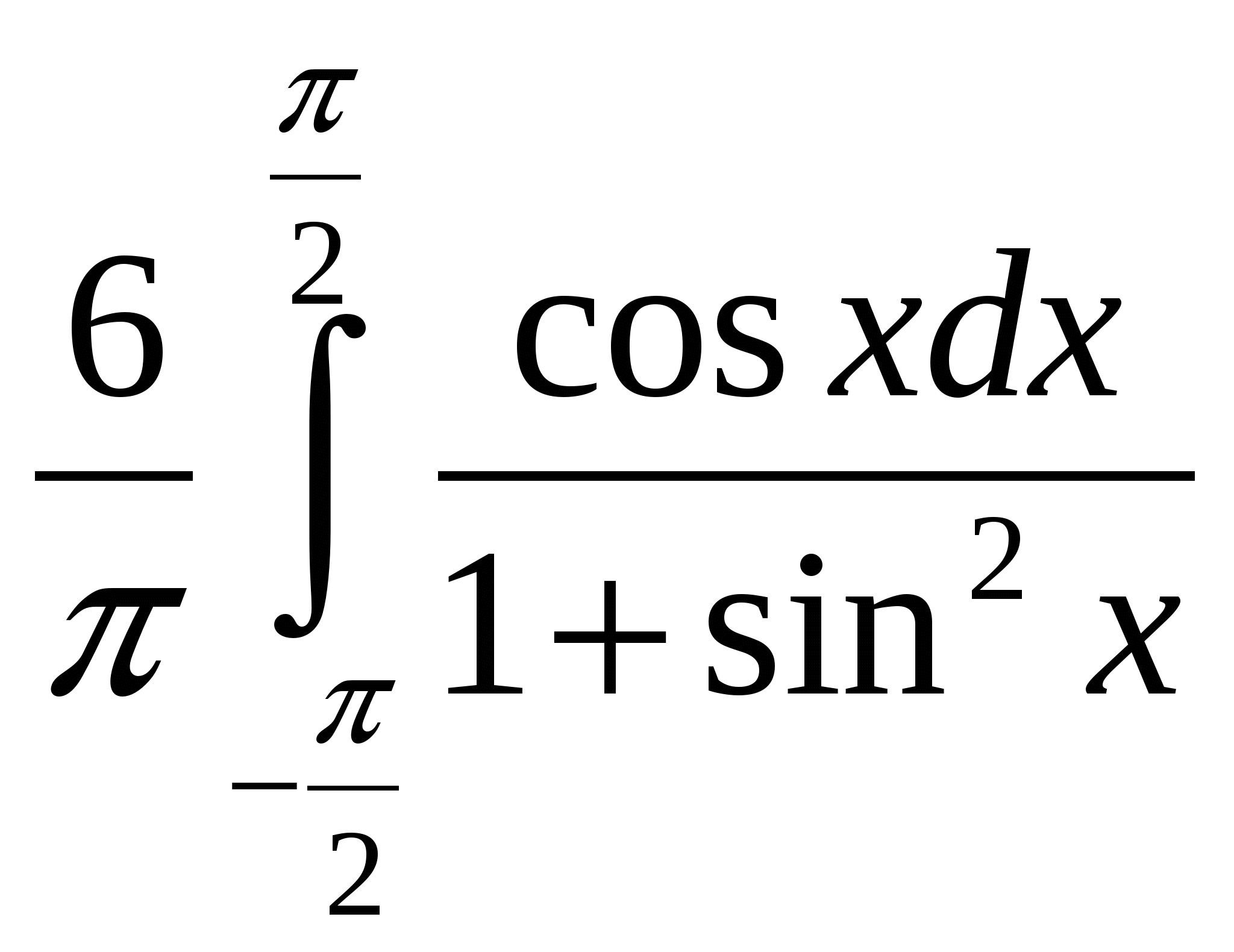 3 3В силу предельного критерия сходимости несобственный интеграл 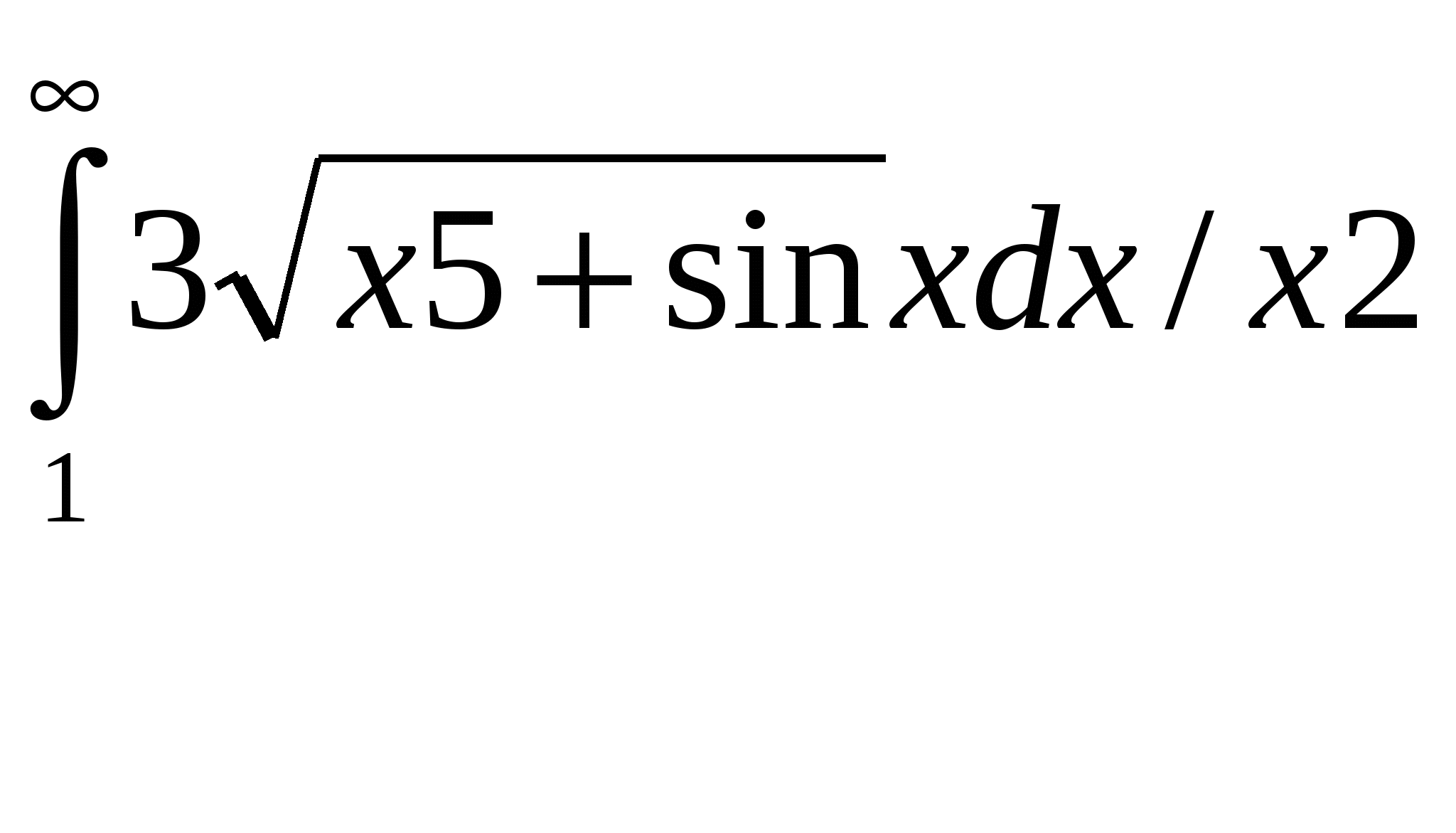 |
