Контрольная работа по математике. Решение а. Используем метод интегрирования частями б. Используем метод замены переменной
 Скачать 286.91 Kb. Скачать 286.91 Kb.
|
|
1. Найти неопределенный интеграл. а). 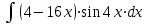 ; б). ; б).  ; в). ; в). 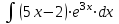 ; г). ; г). 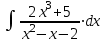 . .Решение. а). Используем метод интегрирования частями: 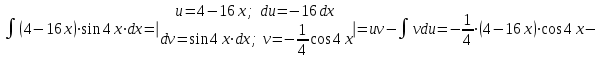 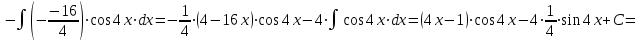 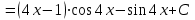 . .б). Используем метод замены переменной: 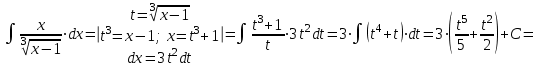 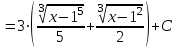 . .в). Используем метод интегрирования частями: 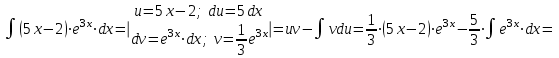 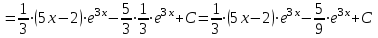 . .г). 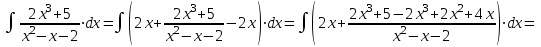 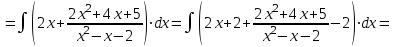  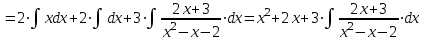 . .Разложим последнее подынтегральное выражение на сумму простейших дробей, используя общий метод разложения. 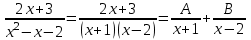 . .Освобождаемся от знаменателей: 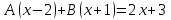 ; ; 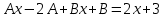 . .Приравнивая коэффициенты при одинаковых степенях х левой и правой части, получим: 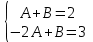 ; ; 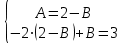 ; ; 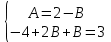 ; ; 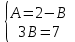 ; ; 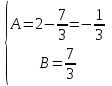 . .Итак, 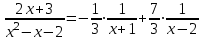 ; ;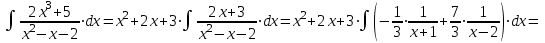 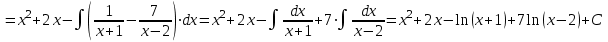 . .2. Вычислить по формулам Ньютона-Лейбница определённый интеграл: а). 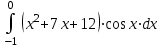 ; б). ; б).  . .Решение. а). Найдем сначала соответствующий неопределённый интеграл, используя метод интегрирования частями: 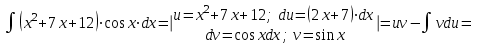 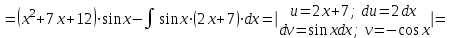 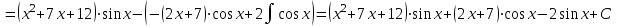 Используя формулу Ньютона-Лейбница, получим: 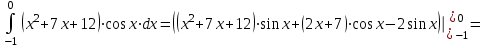 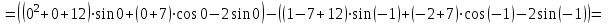 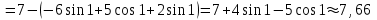 . .б). 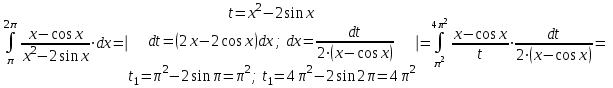 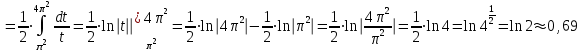 . .3. Вычислить площадь фигуры, ограниченной линиями 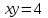 , , 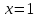 , , 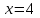 и и 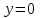 Решение. Сделаем схематический чертеж указанной фигуры, ограниченной гиперболой 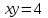 или или 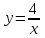 и прямыми и прямыми 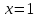 , , 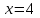 , , 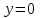 : :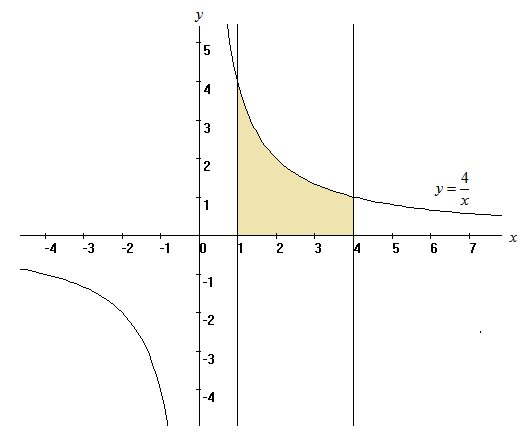 Площадь фигуры (закрашенной на чертеже) будем искать по соответствующей формуле через определенный интеграл, и именно 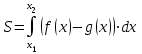 , где , где 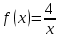 – функция, график которой ограничивает фигуру сверху, – функция, график которой ограничивает фигуру сверху,  – функция, график которой ограничивает фигуру снизу. – функция, график которой ограничивает фигуру снизу.Тогда, получим: 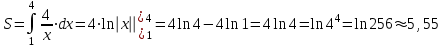 4. Найти полный дифференциал функции 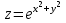 . .Решение. Находим частные производные первого порядка: 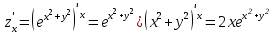 ; ;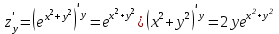 . .По соответствующей формуле запишем полный дифференциал функции: 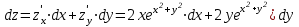 . .5. Исследовать функцию 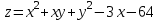 на экстремумы. на экстремумы.Решение. Сначала найдем все частные производные первого порядка: 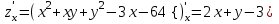 и и 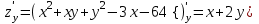 . . Приравнивая их к нулю, получаем систему уравнений: 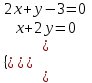 ; ; 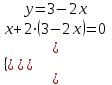 ; ; 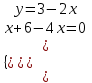 ; ; 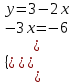 ; ; 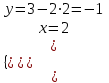 . .Решению системы уравнений соответствует одна стационарная точка: 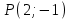 . .Найдем частные производные второго порядка указанной функции: 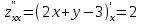 ; ; 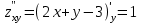 ; ; 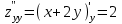 . .Следовательно, вторые производные постоянные величины, т.е. в стационарной точке 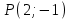 они равны они равны 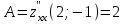 , , 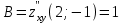 , , 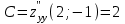 и вычисляем дискриминант и вычисляем дискриминант 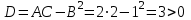 . .Дискриминант имеет положительное значение, следовательно, экстремум в точке 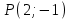 есть и, поскольку есть и, поскольку 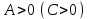 , то функция здесь имеет локальный минимум. , то функция здесь имеет локальный минимум.Вычислим минимальное значение функции в точке 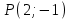 : :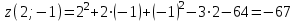 . .Следовательно, в точке 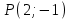 функция имеет минимум равный -67. функция имеет минимум равный -67.6. Найти общее решение дифференциального уравнения 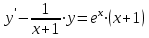 и частное решение, удовлетворяющее начальным условиям и частное решение, удовлетворяющее начальным условиям 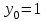 при при 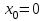 . .Решение. Для решения уравнения используем метод Бернулли. Положим 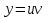 ; тогда ; тогда 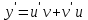 . Подставив выражения . Подставив выражения 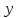 и и 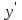 в исходное уравнение, получим: в исходное уравнение, получим: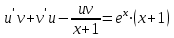 или или 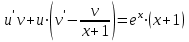 . .Считая, что неизвестная функция 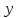 является произведением двух (также неизвестных) функций является произведением двух (также неизвестных) функций 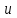 и и 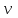 , мы тем самым можем одну из этих функций выбрать произвольно. Поэтому приравняем нулю коэффициент при , мы тем самым можем одну из этих функций выбрать произвольно. Поэтому приравняем нулю коэффициент при 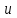 : : 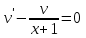 . .Разделяя переменные в полученном уравнении, имеем: 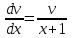 ; ; 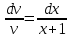 ; ;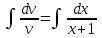 ; ; 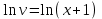 ; ; 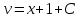 . .Снова в виду произвольности в выборе 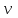 мы можем не учитывать произвольную постоянную мы можем не учитывать произвольную постоянную 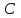 (точнее – можем приравнять её к нулю), т.е. (точнее – можем приравнять её к нулю), т.е. 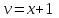 Найденное значение 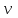 подставляем в уравнение подставляем в уравнение 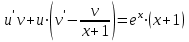 : :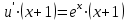 ; ; 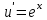 ; ;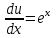 ; ; 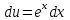 ; ; 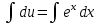 ; ; 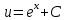 (здесь (здесь 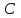 писать обязательно, иначе получится не общее, а частное решение). писать обязательно, иначе получится не общее, а частное решение).Тогда, окончательно получим: 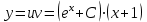 – общее решение уравнения. – общее решение уравнения.Используя начальное условие, получим: 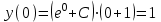 ; ; 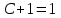 ; ; 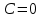 Следовательно, 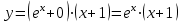 – частное решение. – частное решение.7. а). Найти общее решение уравнения  и частное решение, удовлетворяющее начальным условиям и частное решение, удовлетворяющее начальным условиям 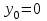 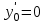 при при 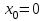 . .б). Найти общее решение уравнения 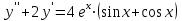 . .Решение. а). Имеем случай понижения порядка – отсутствует переменная у. Вводим замену 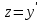 : : 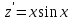 . .Заменяя 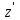 на на 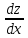 , получим: , получим: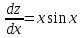 ; ; 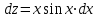 ; ;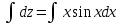 ; ;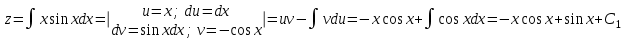 . .Возвращаясь к замене, получим: 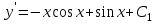 ; ; 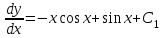 ; ; 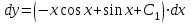 ; ;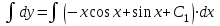 ; ;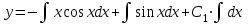 . .Решим отдельно интеграл 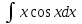 : :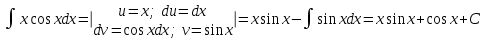 . .Тогда, получим: 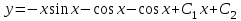 ; ; 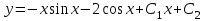 – общее решение уравнения. – общее решение уравнения.Используя начальное условие, находим постоянные 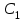 и и 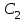 : :1). 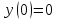 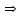 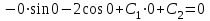 ; ; 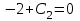 ; ; 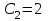 ; ;2). 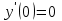 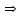 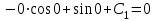 ; ; 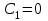 . .Итак, 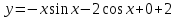 ; ;  – частное решение. – частное решение.б). Составим характеристическое уравнение и найдем его корни: 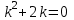 ; ; 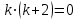 ; ; 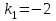 , , 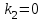 – два неравных действительных корня. – два неравных действительных корня.Тогда, получим общее решение уравнения без правой части: 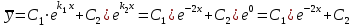 . .Уравнение с правой частью имеет частное решение вида: 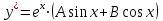 . .Находим коэффициенты 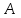 и и 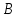 , используя метод неопределенных коэффициентов. , используя метод неопределенных коэффициентов.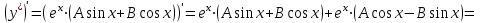 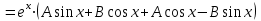 ; ;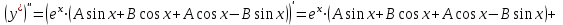 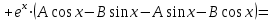 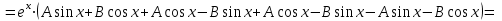 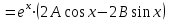 . .Подставляя найденные значения в исходное уравнение, получим: 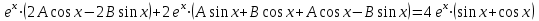 ; ;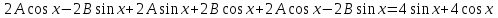 ; ;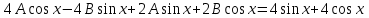 . .Приравнивая одинаковые коэффициенты, получим: 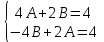 ; ; 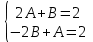 ; ; 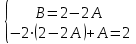 ; ; 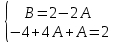 ; ; 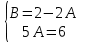 ; ;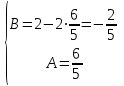 . .Тогда, запишем частное решение:  . .Полное решение заданного уравнения: 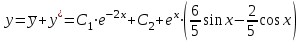 . .8. Найти область сходимости ряда 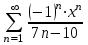 . .Решение. Здесь 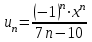 , , 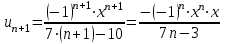 . .Далее, используя признак Даламбера, ищем предел: 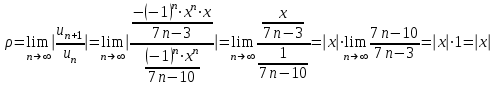 . .И определяем, при каких значениях x этот предел будет меньше единицы, т.е. решаем неравенство: 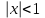 ; ; 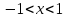 . .Границы найденного интервала исследуем особо. При 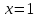 получим числовой знакочередующейся ряд получим числовой знакочередующейся ряд 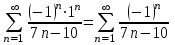 , который сходится по признаку Лейбница: модуль общего члена стремится к 0 – , который сходится по признаку Лейбница: модуль общего члена стремится к 0 – 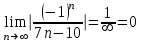 и члены ряда убывают по абсолютному значению с увеличением порядкового номера. и члены ряда убывают по абсолютному значению с увеличением порядкового номера.При 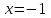 получим числовой положительный ряд получим числовой положительный ряд 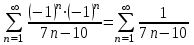 . Используем предельный признак сравнения. Для этого сравним данный ряд с известным расходящимся гармоническим рядом . Используем предельный признак сравнения. Для этого сравним данный ряд с известным расходящимся гармоническим рядом 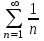 . .Тогда, получим: 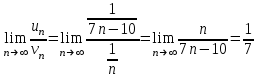 . Поскольку получили конечный ненулевой предел, то заданный ряд также расходится. . Поскольку получили конечный ненулевой предел, то заданный ряд также расходится.Следовательно, область сходимости есть – 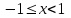 . .9. С точностью до 0,001 вычислить 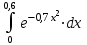 . .Решение. Используя известное разложение функции 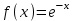 в степенной ряд: в степенной ряд: 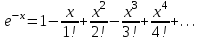 разложим подынтегральную функцию в соответствующий ряд подставив вместо разложим подынтегральную функцию в соответствующий ряд подставив вместо 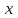 выражение выражение 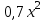 . .Тогда, получим: 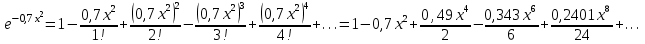 ; ;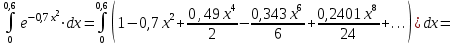 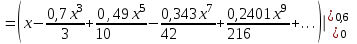 . .Проводим соответствующие вычисления с заданной точностью: 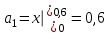 , , 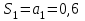 ; ;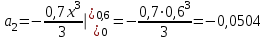 ; ; 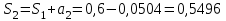 ; ;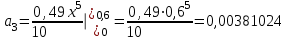 ; ; 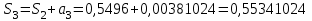 ; ;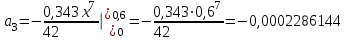 . .Поскольку 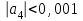 (заданная точность удовлетворяется), то (заданная точность удовлетворяется), то 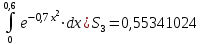 . . |
