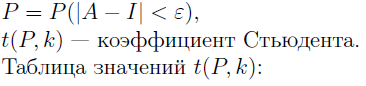Оглавление
Введение 2
1.Теоретическая часть 3
2.Практическая реализация 9
2.1 Проектирование интерфейса 9
2.2 Программирование вычисления 13
2.3 Визуализация метода 14
2.4 Вычислительный эксперимент 15
Заключение 19
Введение
Проект разработан для вычисления приближенных значений интеграла заданной функции по формуле Симпсона методом повторного счета, а также для вычисления приближенных значений интеграла заданной функции методом Монте-Карло. Пояснительная записка состоит из следующих разделов:
1.Теоретическая часть
Квадратическая формула Симпсона:
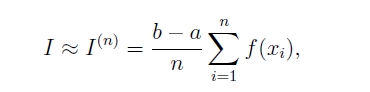
где yi = f(xi), (i = 0,1 ,..., n), xi+1 - xi = h = (b - a)/n, n = 2m
Практическая оценка погрешности при двойном счете (h2 = h1/2):
|I – I2| ≈ |In - I2n| / 15,
Где 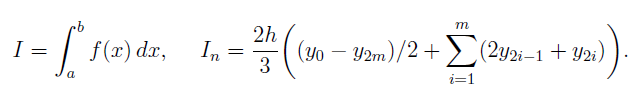
Вычисление определенных интегралов методом Монте-Карло:
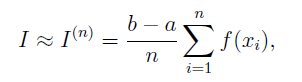
где хi – возможные значения случайно величины Х, распределённой равномерно в интервале [a, b] с плотностью р(х) = 1/ (b - а).
xi = a + (b - a) ri, где ri – случайные числа в [0, 1].
Если n достаточно велико и проведено достаточно большое количество К – испытаний, то согласно центральной предельной теореме, распределения чисел
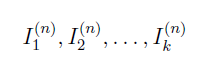
Является асимптотически нормальным. При этом наилучшей реально возможной оценкой величины I является эмпирическое среднее по выборке
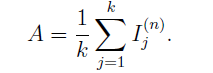
Доверительный интервал для I:
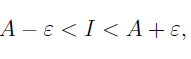
Где значение ε определяется как
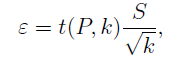
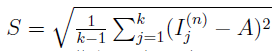 - выборочное среднее квадратическое отклонение. - выборочное среднее квадратическое отклонение.
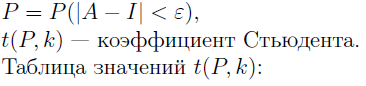
2.Практическая реализация 2.1 Проектирование интерфейса
Сначала создадим главное окно программы, без которой нам никак нельзя обойтись [Error: Reference source not found]. Сделаем в нем главное меню состоящее из пунктов «Ввод», «Решение», «Исследование», «Заставка». На данной форме разместим рисунок, содержащий интеграл, а также разместим командную кнопку для выхода из приложения «Close». Это окно будет являться опорным пунктом для наших дальнейших действий. Обозначим его как Form1. (Рис. 4)

Рис. 4. Form1
Далее, создадим другие «формы» для последующей работы, на которые в дальнейшем просто будем ссылаться:
окно для ввода пределов интегрирования и количества разбиений n – Form2. Выводится при выборе пункта меню «Ввод»:

Рис. 5. Form2
При нажатии на кнопку «ОК» текст из текстовых полей переводится в числовые переменные, и происходит закрытие данного окна.
окно «Решение», появляющееся при выборе одного из пунктов меню (Рис. 6) в

Рис. 6
зависимости от желаемого метода вычисления определённого интеграла – Form3:
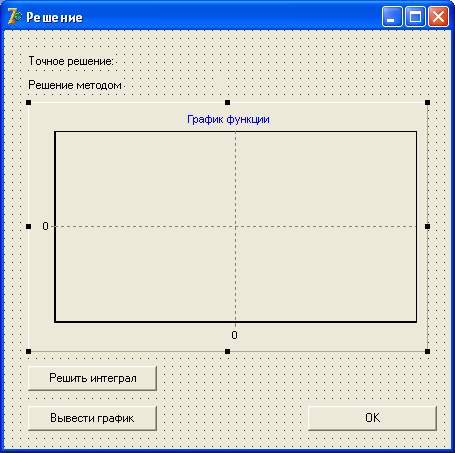
Рис.7. Form3
При нажатии на кнопку «Решить интеграл» рядом с меткой «Точное решение» будет выведено решение интеграла методом Ньютона-Лейбница, ниже будет выведено решение интеграла при помощи метода, выбранного пользователем. При нажатии на кнопку «Вывести график» будет выведен график функции, а также будет проиллюстрирован метод прямоугольников. При нажатии на кнопку «ОК» будет произведено закрытие текущей формы.
окно «Исследование на погрешность» – Form4, вызываемое выбором пункта меню «Исследование»:
Рис.8. Form4
При нажатии на кнопку «Вывести графики» будут выедены графики зависимости уровня погрешности от количества разбиений для метода прямоугольников и метода Симпсона. При нажатии на кнопку «ОК» будет произведено закрытие текущей формы.
окно «Заставка» – Form4, вызываемое выбором пункта меню «Заставка»:

Рис.9. Form5
При нажатии на кнопку «ОК» будет произведено закрытие текущей формы.
Теперь, после того как мы создали все необходимые формы, можем приступать к создании программного кода, в котором будем ссылаться на каждую из них. В этом коде нам необходимо будет:
для Form1 - обеспечить безошибочное подключение ко всем остальным формам.
для Form2 - обеспечить ввод данных, для указания отрезка интегрирования а так же количества разбиений.
для Form3 - обеспечить вывод результата точного подсчета, а также результата подсчета одним из методов, кроме того, для наглядности, необходимо продемонстрировать визуализацию метода прямоугольников.
для Form4 - исследовать единую эффективность методов прямоугольников и Симпсона, при помощи их визуального сравнения.
для Form5 - включить в программу.
2.2 Программирование вычисления
Для вычисления определённого интеграла методом прямоугольников используется подпрограмма – процедура pramoug (a,b: real; n: integer; var s:real). Она составлена по блок схеме представленной выше (1 теоретическая часть). Процедуре нужно сообщить начало и конец промежутка интегрирования, а также количество разбиений, результат процедуры – значение определённого интеграла, полученное по формуле прямоугольников.
procedure pramoug (a,b: real; n: integer; var s:real);
var
h,f,x: real; i: integer;
begin
h:=(b-a)/n;
x:=a+h;
S:=0;
for i:=0 to n-1 do
begin
F:=(1/(x*x))*sin(1/x);
s:=s+f;
x:=x+h;
end;
s:=s*h;
end;
Для вычисления определённого интеграла методом Симпсона используется подпрограмма – процедура Simpson (a,b: real; n: integer; var s2:real). Она составлена по блок схеме представленной выше (1 теоретическая часть). Процедуре нужно сообщить начало и конец промежутка интегрирования, а также количество разбиений, результат процедуры – значение определённого интеграла, полученное по формуле Симпсона.
procedure Simpson (a,b: real; n: integer; var s2:real);
var
h,c,f,x: real; i: integer;
begin
if (n mod 2)=1 then n:=n-1;
h:=(b-a)/n;
s2:=0;
c:=1;
x:=a;
For i:=1 to n-1 do
begin
x:=x+h;
f:=(1/(x*x))*sin(1/x);
s2:=S2+(3+c)*f;
c:=-c;
end;
s2:=h*((1/(a*a))*sin(1/a)+(1/(b*b))*sin(1/b)+s2)/3;
end;
В обоих случаях начальные данные - это начало и конец промежутка интегрирования, а также количество разбиений. В первом случае получаем результат для метода прямоугольников, во втором - для метода Симпсона.
2.3 Визуализация метода
В главном окне выберем пункт меню «Исследование»;
При нажатии на кнопку «Вывести графики» будут выедены графики зависимости уровня погрешности от количества разбиений для метода прямоугольников (график красного цвета) и метода Симпсона (график зелёного цвета).
Построение графиков осуществляется в программном коде, следующем ниже:
procedure TForm4.Button1Click(Sender: TObject);
var x:real;
begin
chart1.Visible:=true;
Series1.Clear; {Построение графика для метода прямоугольников}
x:=10;
while x<=200 do
begin
pramoug(a,b,ceil(x),IntPr);
series1.AddXY(x,abs(MNL-IntPr),'',clred);
x:=x+10;
end;
Series2.Clear; {Построение графика для метода Симпсона}
x:=10;
while x<=200 do
begin
Simpson(a,b,ceil(x),IntS);
series2.AddXY(x,abs(MNL-IntS),'',clgreen);
x:=x+10;
end;
end;
Построение ведется на промежутке от 10 до 200. Во время своей работы процедура procedure TForm4.Button1Click(Sender: TObject) обращается к процедурам pramoug (a,b: real; n: integer; var s:real) и Simpson (a,b: real; n: integer; var s2:real), поэтому необходимо, чтобы данные процедуры присутствовали в текущем Unit4.
2.4 Вычислительный эксперимент
Запуская программу, появляется главное окно:

Рис.10. Главное окно.
На нём, как и задумывалось, обозначены: главное меню, состоящее из пунктов «Ввод», «Решение», «Исследование» и «Заставка». После выбора пункта главного меню «Ввод» откроется окно
Рис.11. Окно ввода данных.
В данном окне нужно указать начало и конец промежутка интегрирования, а также количество разбиений. После выполнения этих действий нужно нажать на кнопку «ОК».
Далее в пункте главного меню «Решение» нужно выбрать подпункт «Методом прямоугольников» или подпункт «Методом Симпсона», который определит, при помощи какого метода будет вычисляться определённый интеграл. После щелчка на нужный пункт перед нами появится окно
Рис.12. Решение.
Далее нужно нажать на кнопку «Решить интеграл», после чего в верхней части текущего окна появится точное значение, подсчитанное по формуле Ньютона-Лейбница, а также значение, полученное по формуле выбранного метода. При нажатии на кнопку «Вывести график» в середине окна появится график функции с наглядным изображением метода прямоугольников, при условии выбора данного метода решения, или просто график функции при выборе метода Симпсона. Данное окно после выполнения перечисленных действий будет выглядеть следующим образом
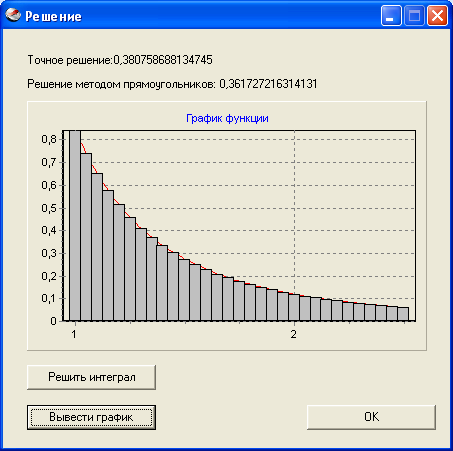
Рис.13. Решение методом прямоугольников.
Далее, выбирая пункт меню «Исследование», мы открываем окно, где после щелчка на кнопке «Вывести графики» будут выведены графики зависимости уровня погрешности от количества разбиений для метода прямоугольников (график красного цвета) и метода Симпсона (график зелёного цвета). Под погрешностью подразумевается взятая по модулю разность между точным значением, полученным по формуле Ньютона-Лейбница, и приближённым значением, полученным по формуле прямоугольников или Симпсона, при данном количестве разбиений n, которое меняется в цикле от 10 до 200.
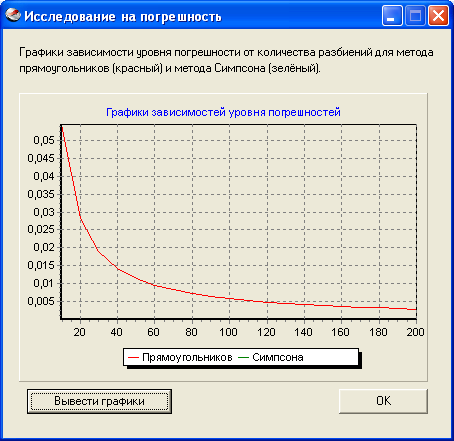
Рис.14. Исследование на погрешность.
Стоит отметить, что в данной программе реализованы функции, предусматривающие обработку исключительных ситуаций, которые могут вызвать сбои в работе программы, при возникновении которых выводится информационное окно с рекомендациями по устранению возникающих неполадок.
Заключение
Проект разработан для вычисления определённого интеграла методами прямоугольников и Симпсона в среде программирования Delphi.
Спроектирован интерфейс программы и написан программный код на языке высокого уровня.
Проведена визуализация метода прямоугольников и анализ данных методов на погрешность вычислений.
В ходе проведения исследования на погрешность было также установлено, что точность вычисления определённого интеграла по формуле Симпсона намного превосходит точность вычисления определённого интеграла по формуле прямоугольников, о чём свидетельствуют графики зависимости уровня погрешности от количества разбиений для метода прямоугольников и метода Симпсона. |
 Скачать 231.77 Kb.
Скачать 231.77 Kb.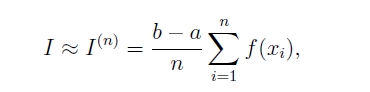
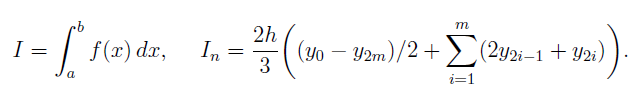
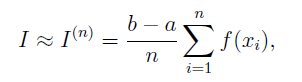
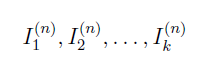
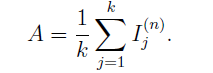
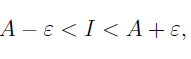

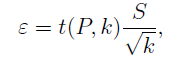
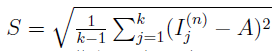 - выборочное среднее квадратическое отклонение.
- выборочное среднее квадратическое отклонение.