вар 4. ВАРИАНТ 4. Задача 264. С помощью двойного интеграла вычислить объем тела ограниченного заданными поверхностями. Решение
 Скачать 72.89 Kb. Скачать 72.89 Kb.
|
|
Контрольная работа 7 Кратные и криволинейные интегралы Задача 264. С помощью двойного интеграла вычислить объем тела ограниченного заданными поверхностями. 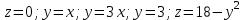 Решение: Сделаем чертеж в плоскости ОХУ: 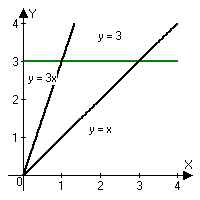 Объем тела Т равен двойному интегралу: 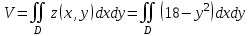 Область D изображена на рисунке. Расставим пределы интегрирования и получим двукратный интеграл:  . При вычислении внутреннего интеграла по х с переменной у обращаемся как с константой: . При вычислении внутреннего интеграла по х с переменной у обращаемся как с константой: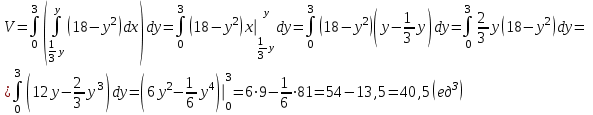 Задача 274. Вычислить работу силового поля  при обходе против часовой стрелки треугольного контура с вершинами А(1,2), В(4,2), С(2,4). при обходе против часовой стрелки треугольного контура с вершинами А(1,2), В(4,2), С(2,4).Решение: 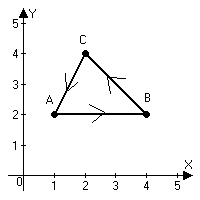 Найдем уравнение стороны АВ: 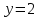 Уравнение стороны ВС: 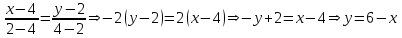 Уравнение стороны АС:  Получим 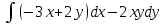 Разобьем этот интеграл по замкнутому контуру на три интеграла, соответствующих отрезкам АВ, ВС, СА:  Учтем, что на отрезке: АВ:  , х изменяется от 1 до 4. , х изменяется от 1 до 4.ВС: 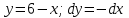 , х изменяется от 4 до 2. , х изменяется от 4 до 2.СА:  , х изменяется от 2 до 1. , х изменяется от 2 до 1.Тогда:  Контрольная работа 8 Ряды Задача 284. Задан числовой ряд  . Составить формулу общего члена ряда. Вычислить частичные суммы ряда . Составить формулу общего члена ряда. Вычислить частичные суммы ряда  . Вычислить сумму ряда. . Вычислить сумму ряда.Решение: Формула общего члена ряда: 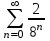 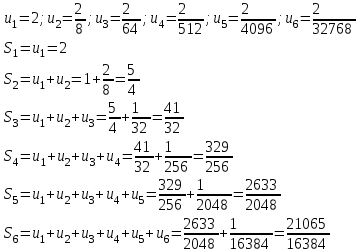 Сумма ряда: 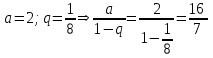 Задача 294. Вычислить приближенно с точностью 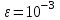 функцию Лапласа функцию Лапласа 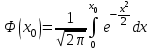 при заданном значении аргумента при заданном значении аргумента  . .Решение: Используем разложение: 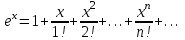 Получим: 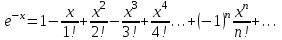 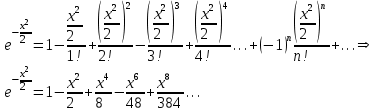 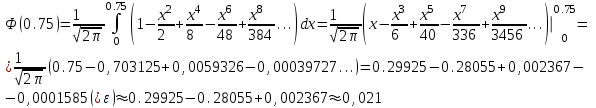 Задача 304. Найти четыре первых члена разложения в ряд Маклорена решения задачи Коши 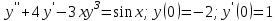 . .Решение:  Дано: 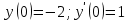 , подставляем: , подставляем: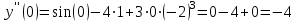 Дифференцируем: 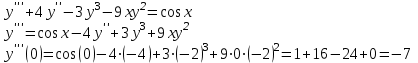 Окончательно получим разложение: 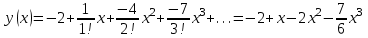 |
