Белоногин А. Определенный интеграл и его свойства. Методы вычисления

• Название: Определенный интеграл и его свойства. Методы вычисления
• Дата: 24.12.2021
• Размер: 140 Kb.
• Имя файла: Белоногин А.doc
• Тип: Документы; #316619

ГОСУДАРСТВЕННОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«КОМСОМОЛЬСКИЙ ИНДУСТРИАЛЬНЫЙ ТЕХНИКУМ»

Дисциплина: ЕН.01 Математика

Группа: СЭС-21

Дата: 08.11.21

Преподаватель: Кулага Т.Ф.
Тема занятия: Определенный интеграл и его свойства. Методы вычисления.

Цели:

Обучающие: ввести понятие определенного интеграла, свойства определенного интеграла, формулу Ньютона-Лейбница, определенный интеграл с переменным верхним пределом, геометрический смысл определенного интеграла;

Воспитательные: создание условий для формирования толерантности, объективной самооценки, ответственности за выполненную работу;

Развивающие: создание условий для развития математически-творческих способностей, логического мышления, математической речи, самостоятельности.

Определенный интеграл и его свойства. Методы вычисления.

Определенный интеграл как предел интегральной суммы

Пусть функция y=f(x) определена на отрезке [a, b], a. Выполним следующие действия: разобьем отрезок [a, b] точками а=х₀,х₁…,х_n=b (х₀<х₁<…<х_n) на n частичных отрезков [x₀, x₁], [x₁, x₂],… [x_n-1, x_n]; в каждом частичном отрезке [x_i-1, x_i] возьмем произвольную точку с_i и вычислим f(c_i); умножим f(c_i) на длину соответствующего частичного отрезка x_i=x_i–x_i-1: f(c_i)x_i и составим сумму всех таких произведений. Сумма всех таких произведений называется интегральной суммой функции y=f(x) на отрезке [a, b]. Найдем предел интегральной суммы, когда n→ ∞ или maxx_i→0.

Если при этом интегральная сумма имеет предел I, который не зависит от способа разбиения отрезка на частичные отрезки, ни от выбора в них, то число I называют определенным интегралом и обозначается .

Таким образом, .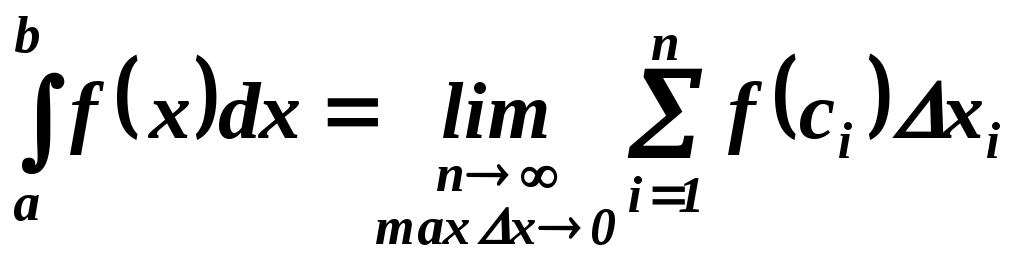

Числа а и b называются, соответственно, нижним и верхним пределами интегрирования, f(x) – подынтегральной функцией, х– подынтегральной функцией, отрезок [a, b] – областью (отрезком) интегрирования.

Функция у= f(x), для которой на отрезке [a, b] существует определенный интеграл , называется интегрируемой на этом отрезке.

Свойства определенного интеграла

1. 
   Определенный интеграл не зависит от обозначения переменной интегрирования:
   
2. 
   Определенный интеграл с одинаковыми пределами равен нулю: .
   
3. 
   .
   
4. 
   при .
   
5. 
   Если с – постоянное число и функция f(x) интегрируема на отрезке [a, b], то , т. е.постоянный множитель с можно вынести за знак определенного интеграла.
   
6. 
   Если функции f₁(x) и f₂(x) интегрируемы на [a, b],тогда
   

, т. е. интеграл от суммы равен сумме интегралов.

7. 
   Свойство аддитивности. Если f(x) интегрируема на отрезке [a, b] и a, то , т. е. интеграл по всему отрезку равен сумме интегралов по частям этого отрезка.
   

8. Если на отрезке [а, b], где аmo u , т.е. обе части неравенства можно почленно интегрировать.

9. Пусть на отрезке [а, b], где a, т≤ f(x)≤M, где т и М – некоторые числа. Тогда .

10. (Теорема о среднем). Если функция y=f(x) непрерывна на отрезке [а, b], (где а < b), то найдется такое значение c∈[a, b], что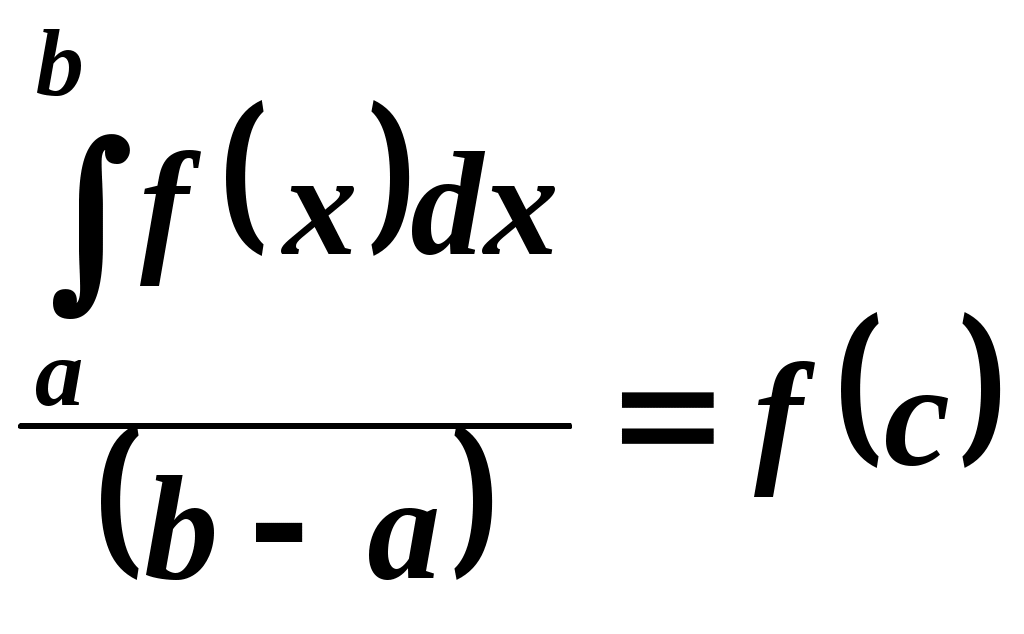

или .

Геометрический смысл определенного интеграла

Пусть на отрезке [a, b] задана непрерывная функция y=f(x)≥0. Фигура ограниченная сверху графиком функции, снизу – осью Ох, сбоку – прямыми х=а, х=b, называется криволинейной трапецией.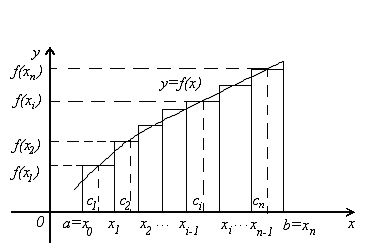



Рассмотрим функцию y=f(x), которая определена на отрезке [a, b]. Разобьем отрезок [a, b] точками а=х₀,х₁…,х_n=b (х₀<х₁<…<х_n) на n частичных отрезков, в каждом из которых возьмем произвольную точкус_i. Умножим f(c_i) на длину соответствующего частичного отрезка x_i. Сумма всех таких произведений равна площади ступенчатой фигуры и приближенно равна площади криволинейной трапеции . За точное значение площади криволинейной трапеции принимают предел S, к которому стремится площадь ступенчатой фигуры S_n, когда n стремится к ∞:

.

Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.