1
|
Символом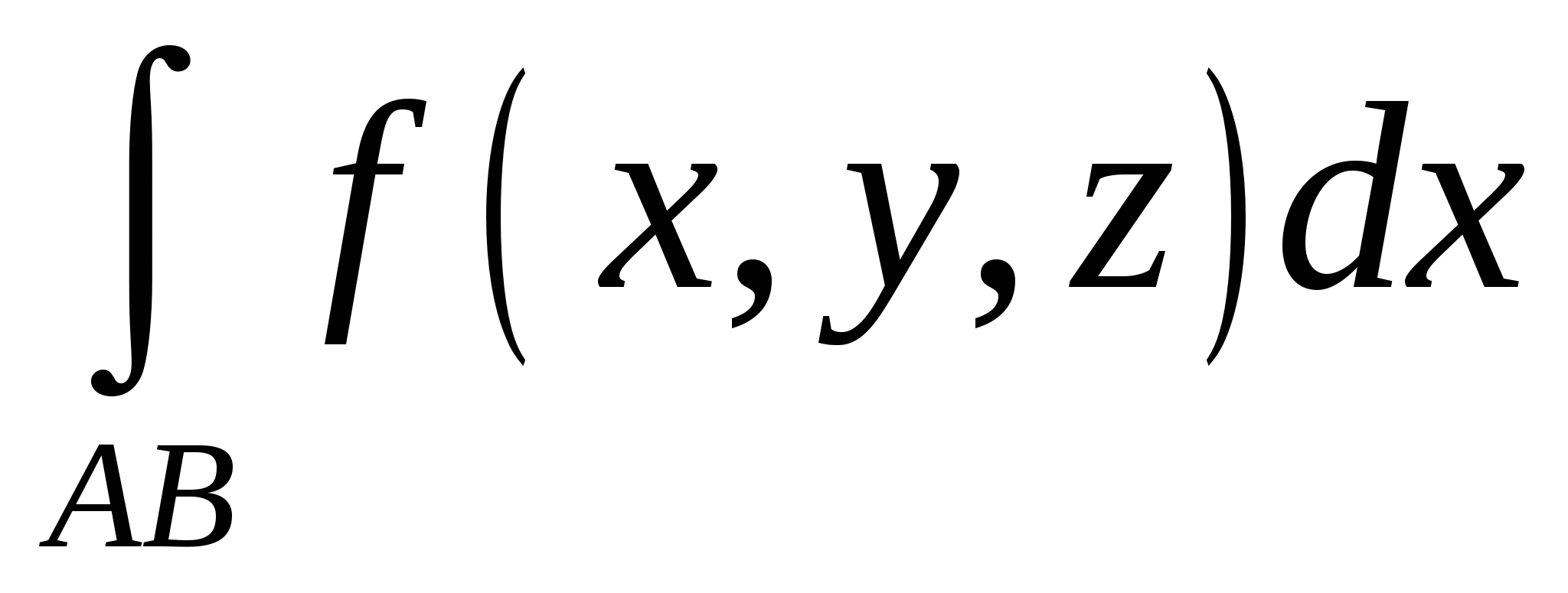
обозначается…
|
1. криволинейный интеграл 1 рода от функции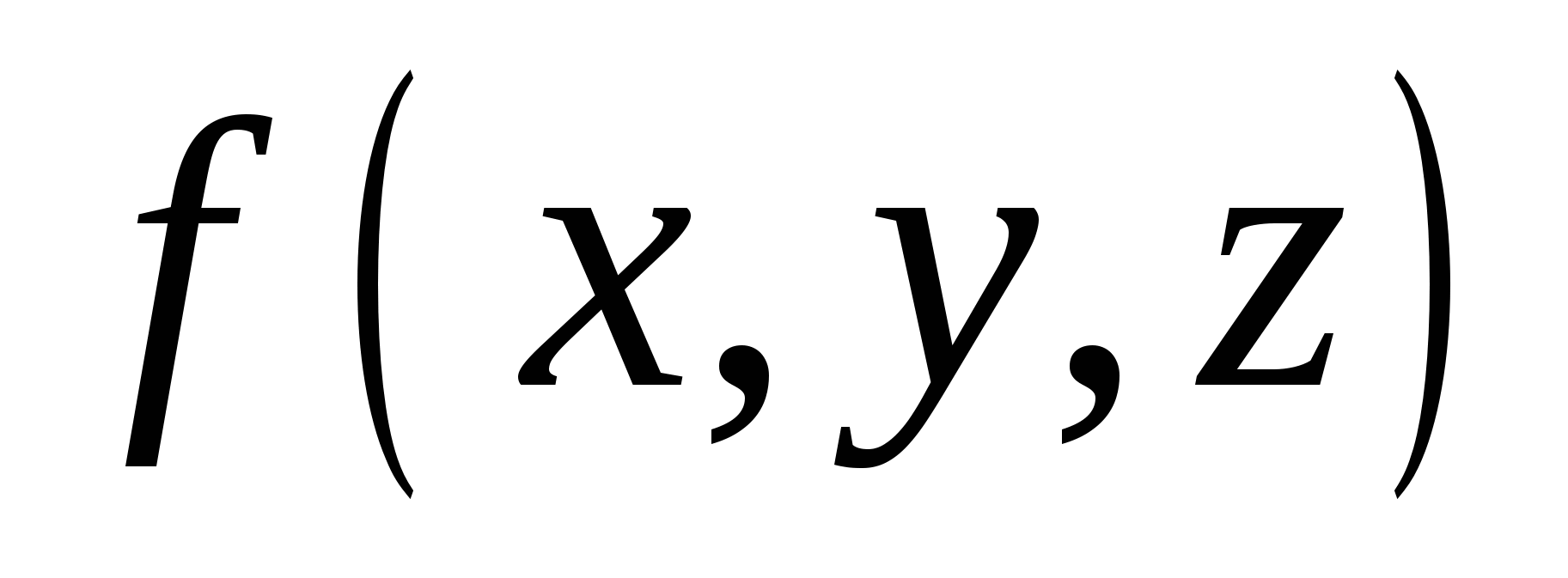 по кривой по кривой 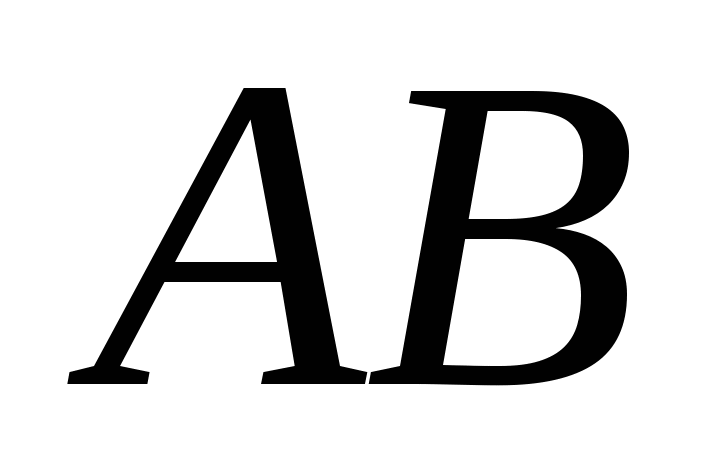 ; ;
2. двойной интеграл;
3. линейный интеграл;
4. криволинейный интеграл 2 рода по переменной 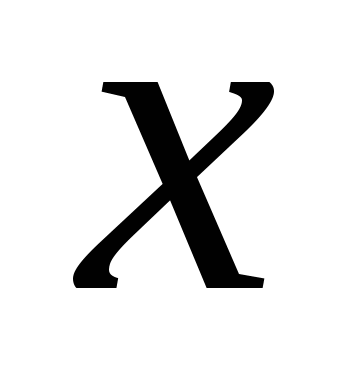 по кривой по кривой  . .
|
2
|
Криволинейный интеграл 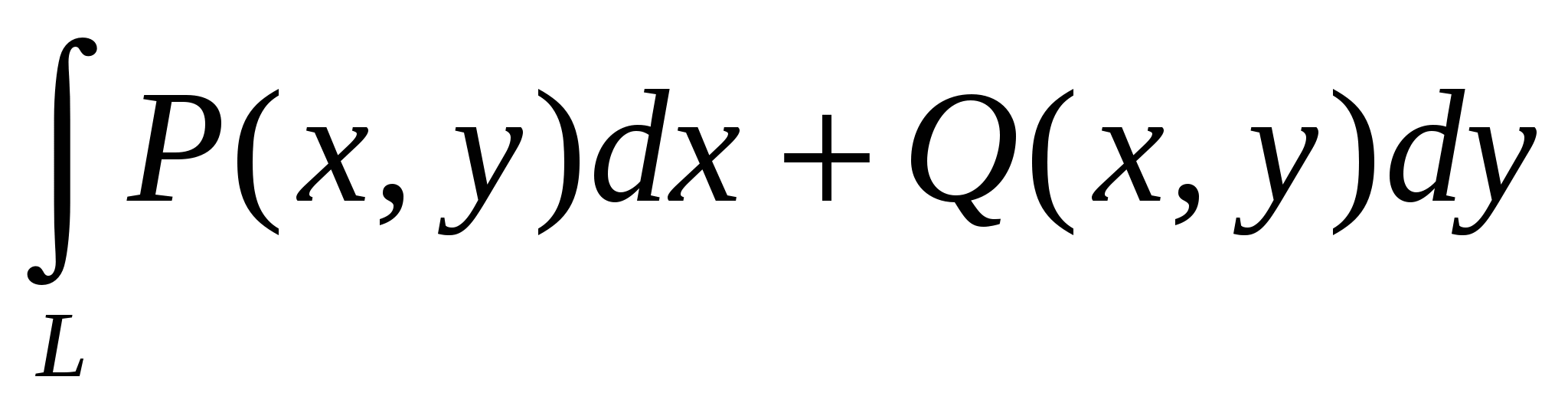 второго рода по дуге контура L, заданного уравнением второго рода по дуге контура L, заданного уравнением
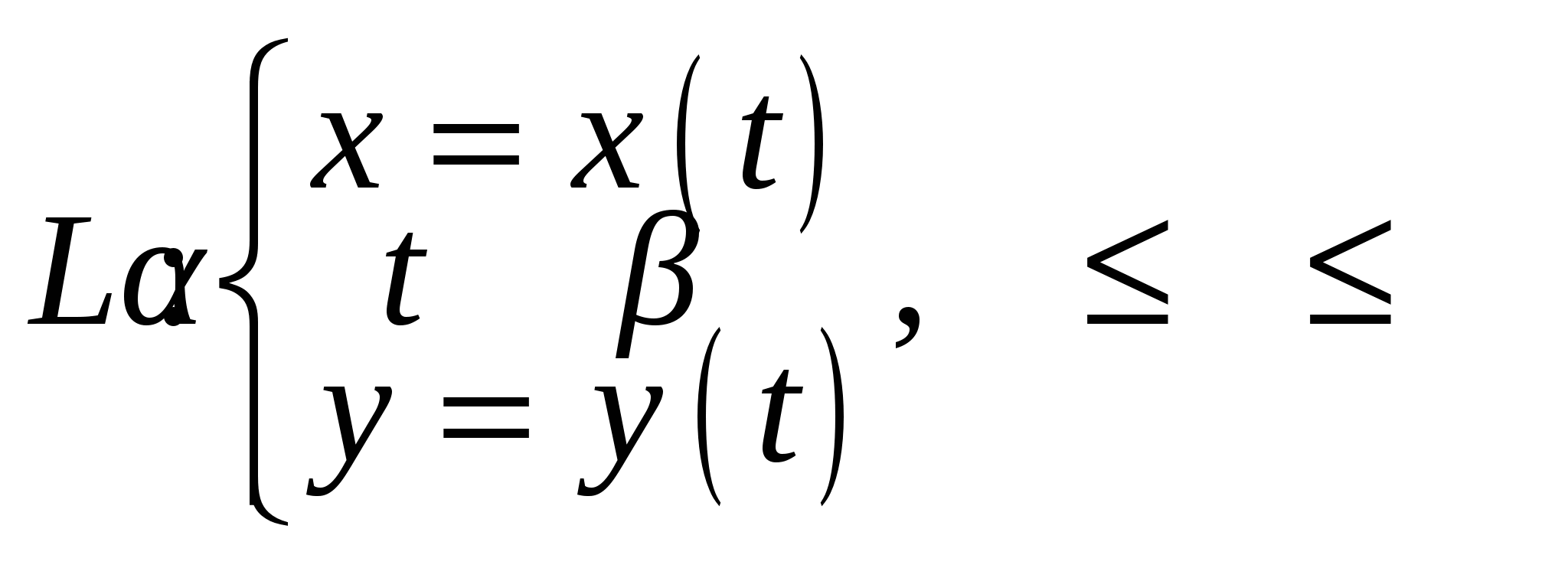 равен…. равен….
|
1. 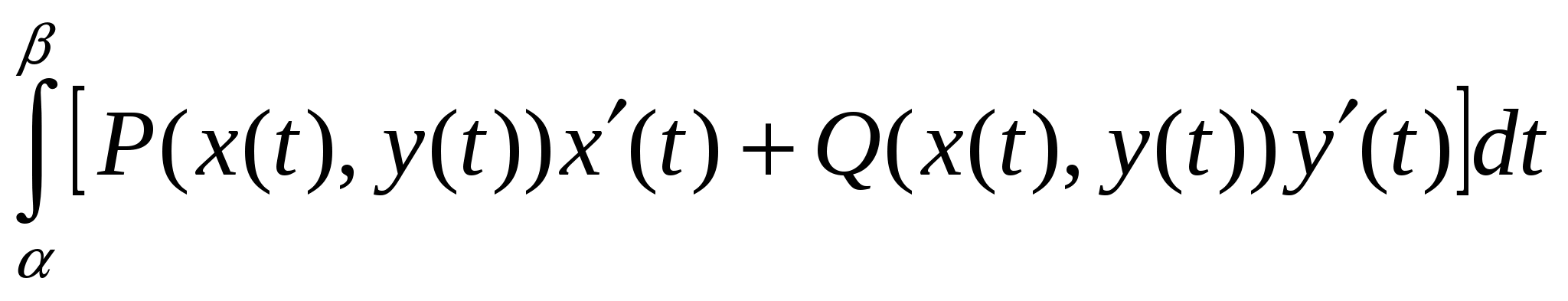 ; ;
2.  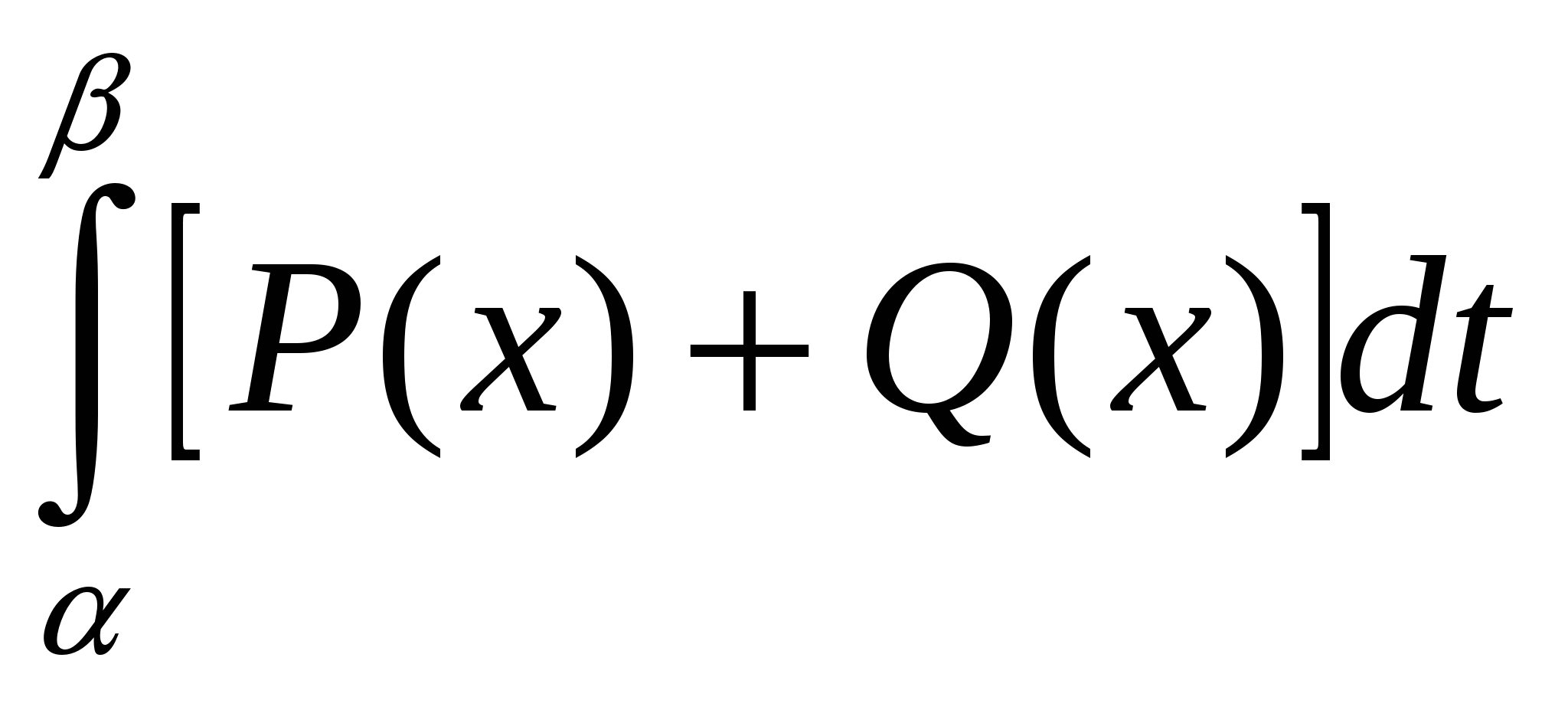 ; ;
3. 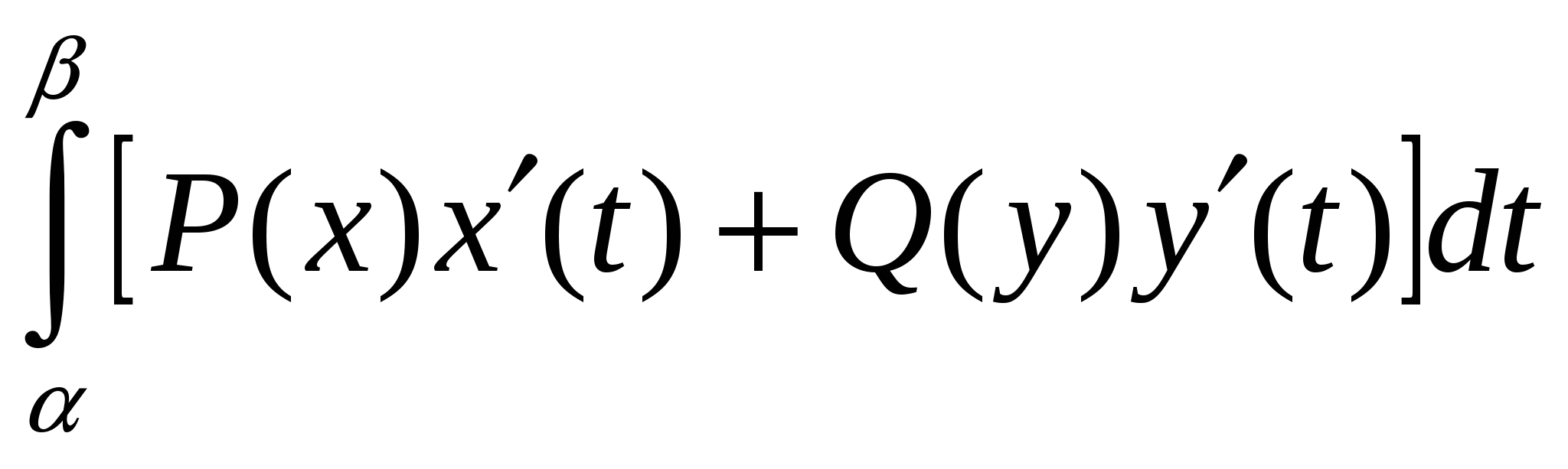 ; ;
4. 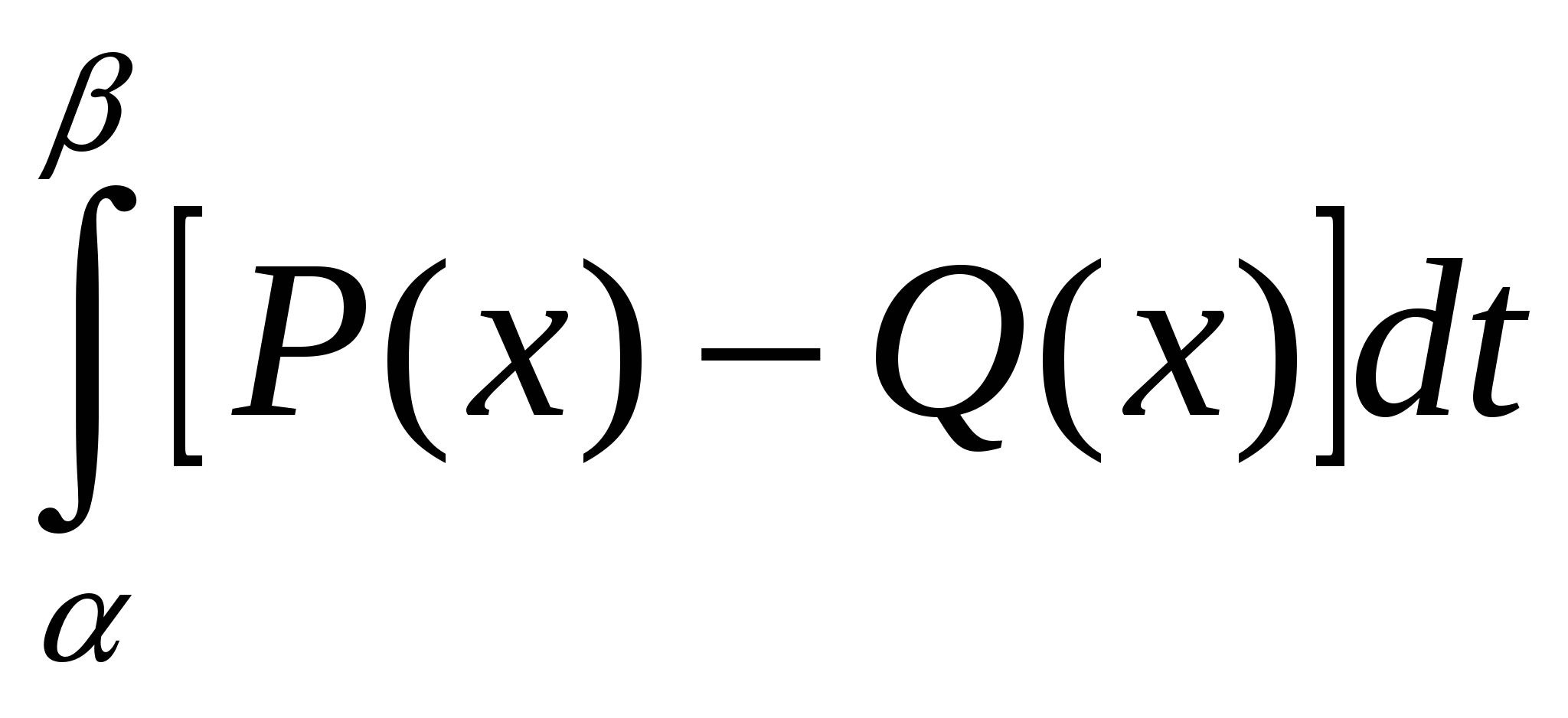 . .
|
3
|
Вычислить 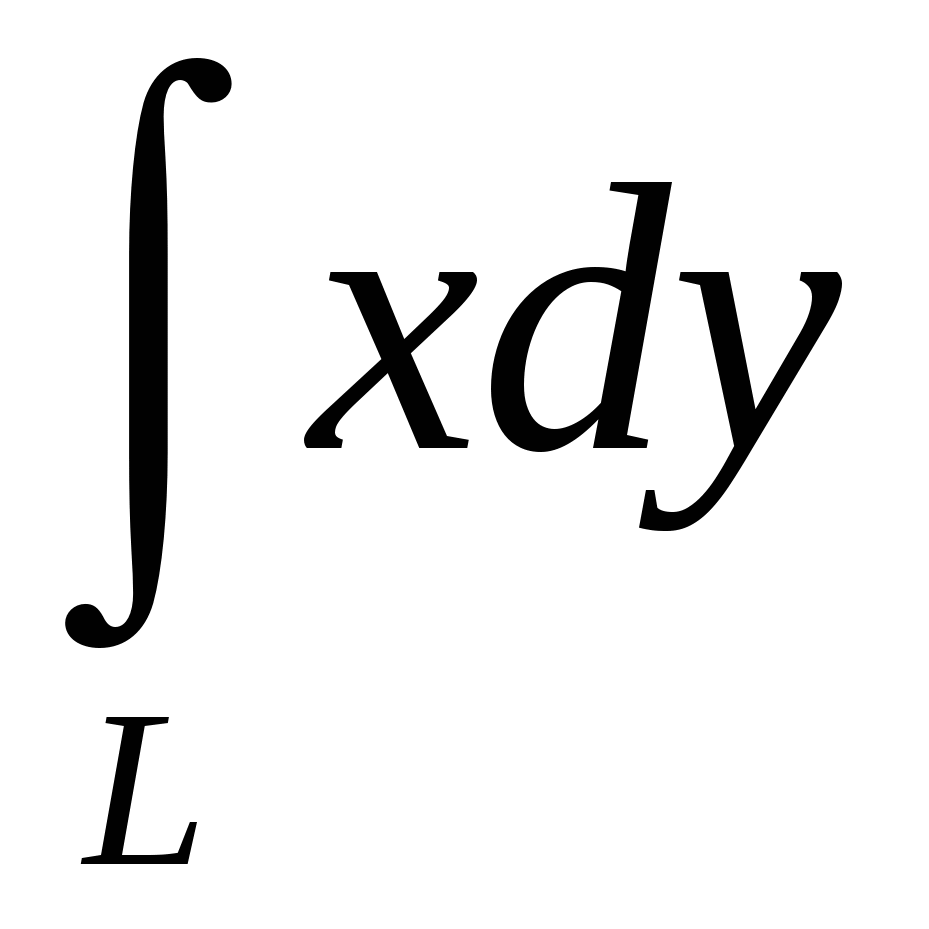 , где L-верхняя половина эллипса, заданного в параметрическом виде: , где L-верхняя половина эллипса, заданного в параметрическом виде:
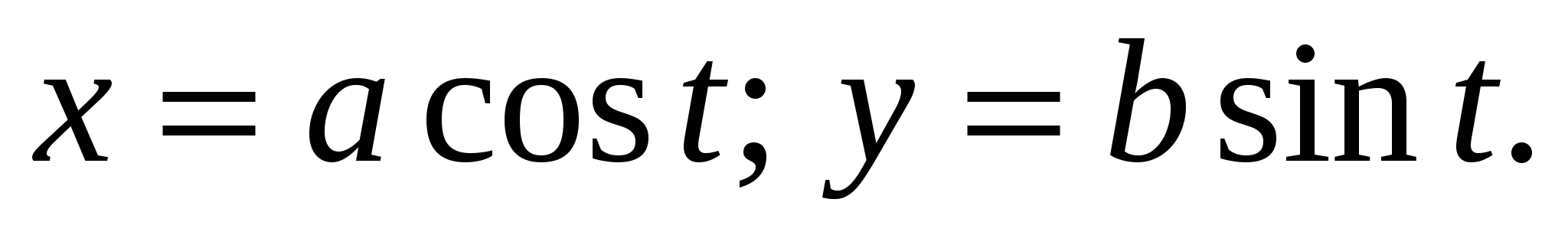
|
1. ab;
2. cost+sint;
3. 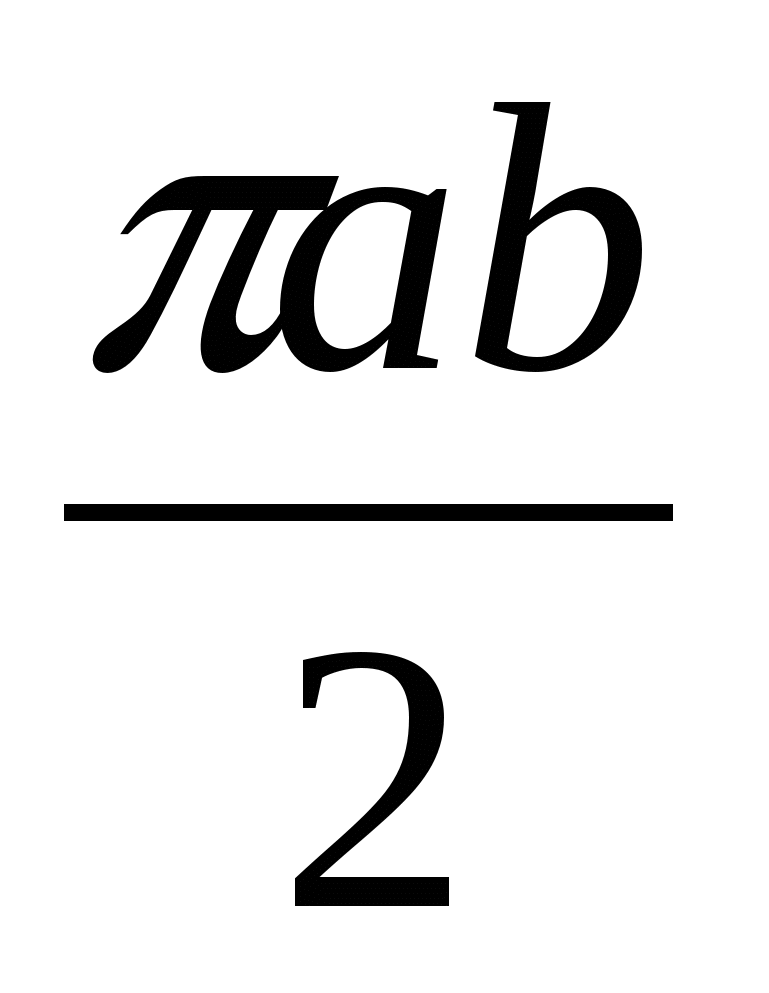 ; ;
4. 2π.
|
4
|
Площадь Sобласти на плоскости xOy, ограниченной контуром L , (контур обходится в положительном направлении), вычисляется по формуле:
|
1.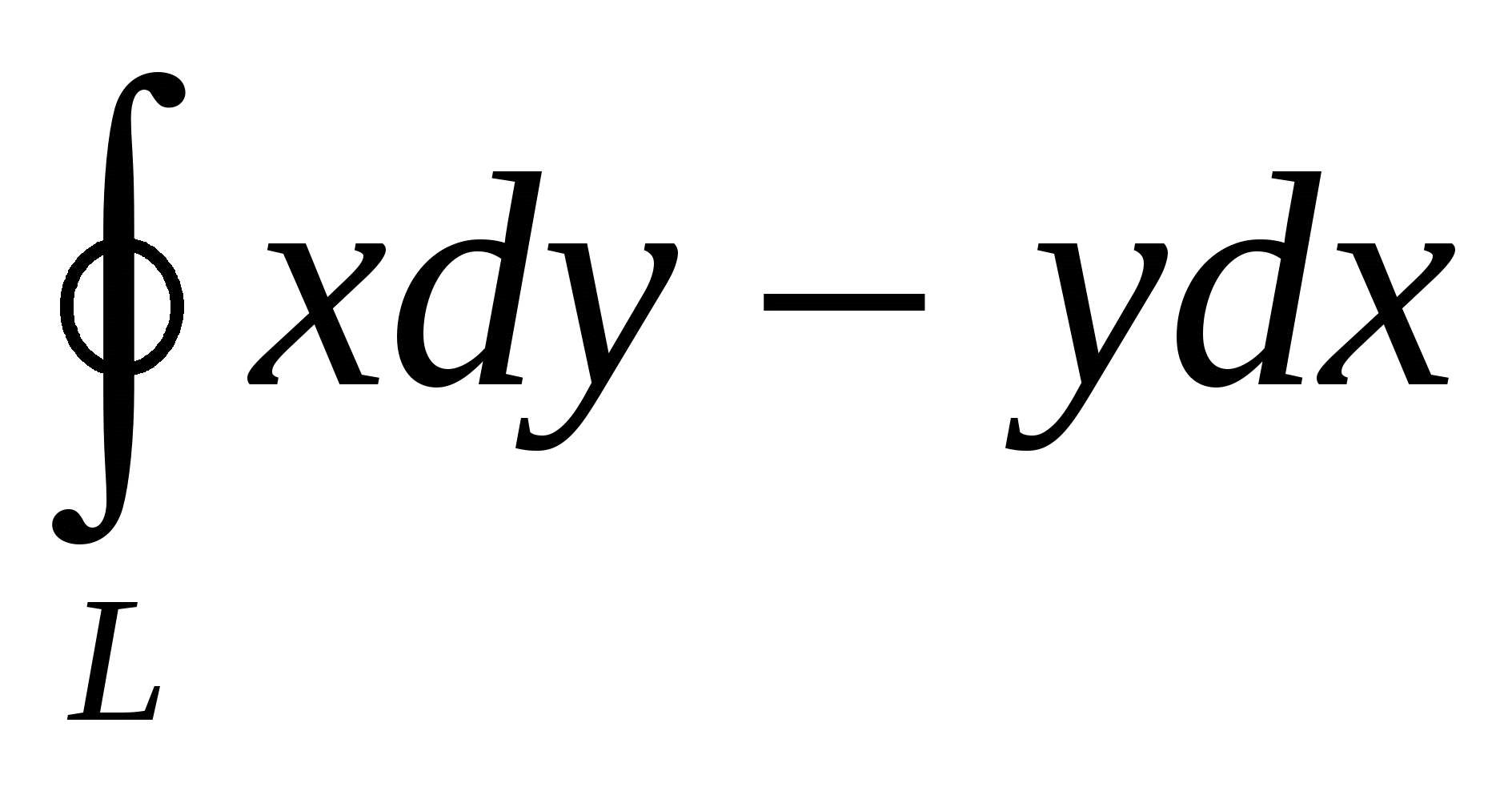 ; ;
2.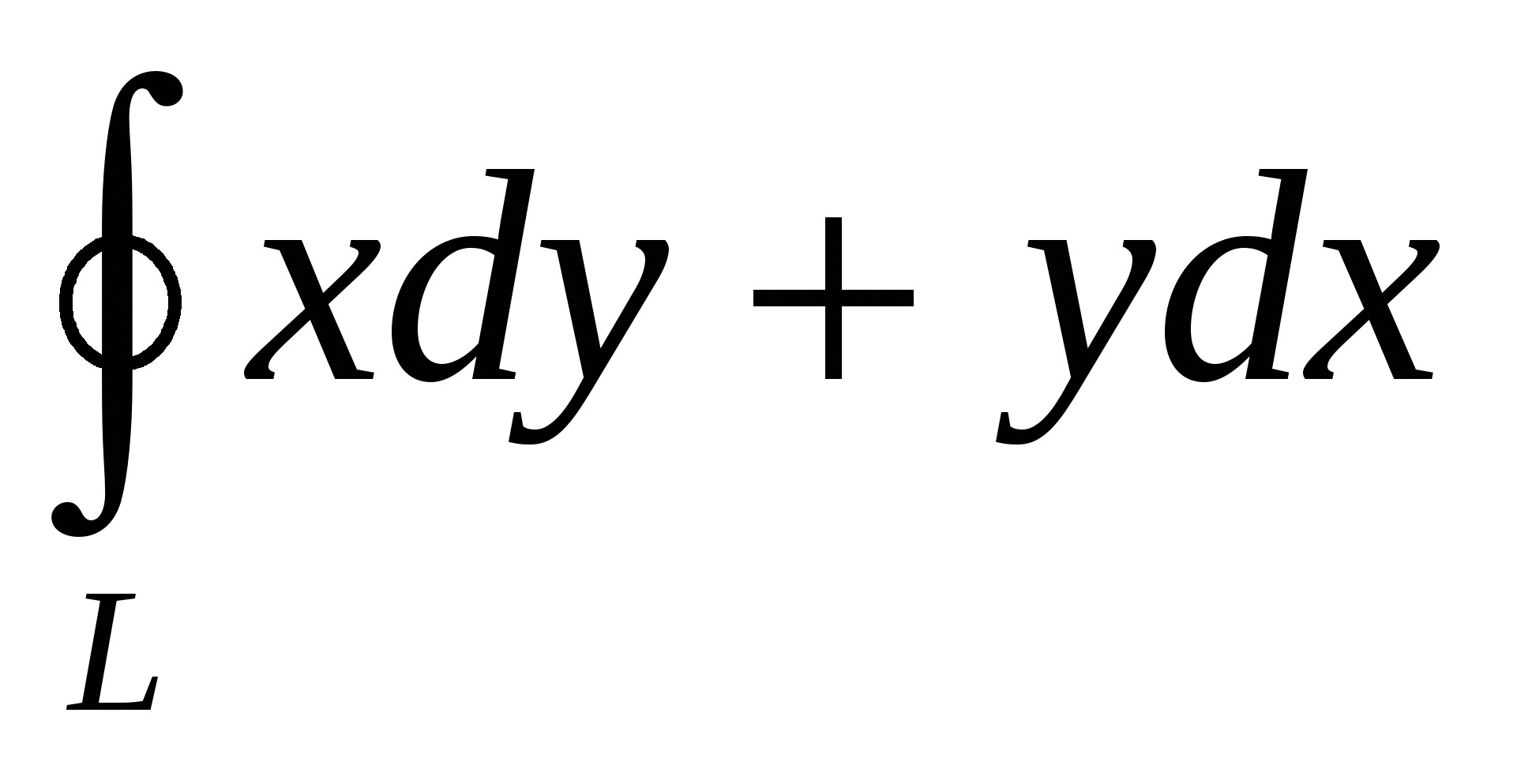 ; 3. ; 3.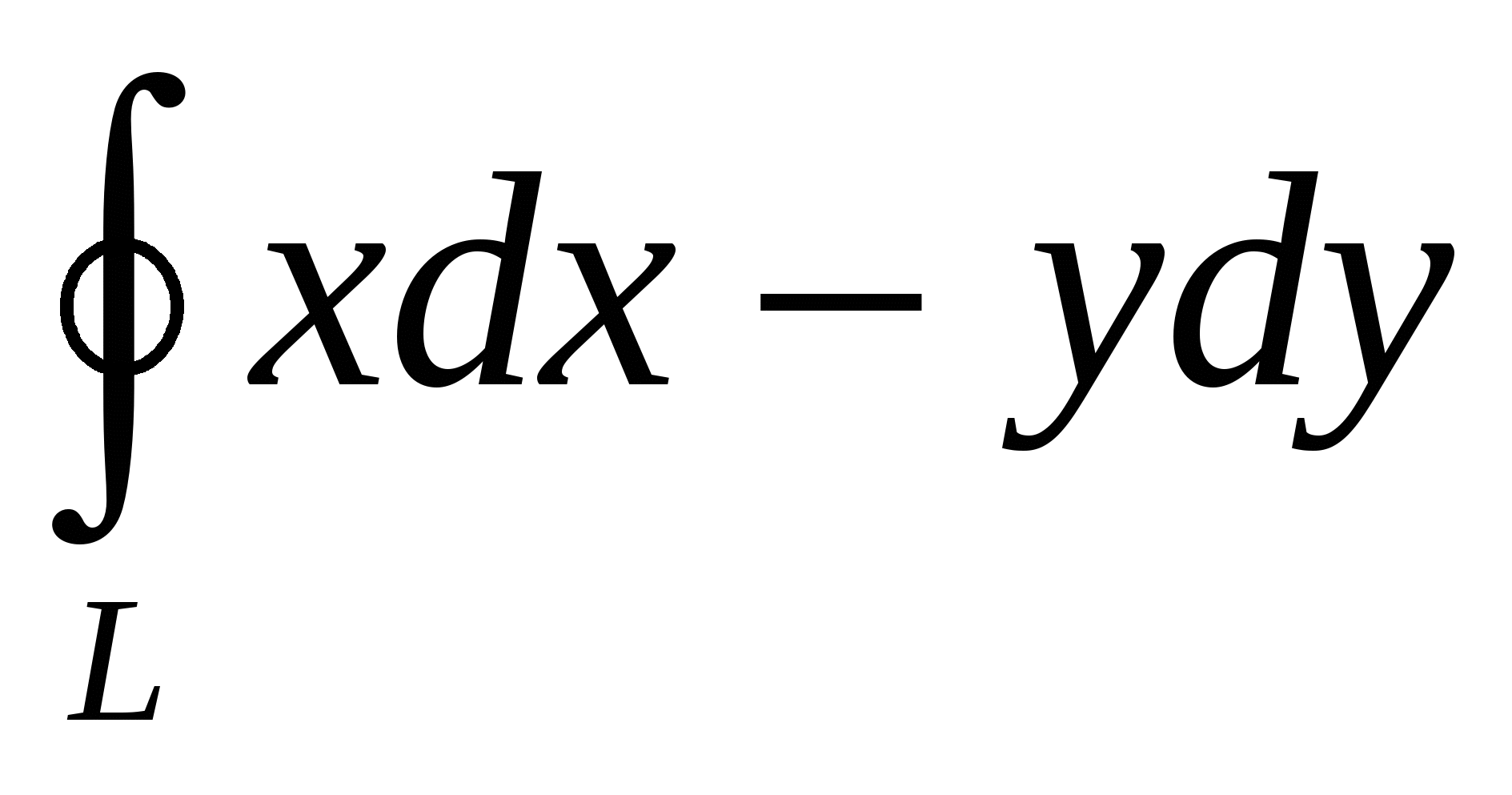 ; ;
4.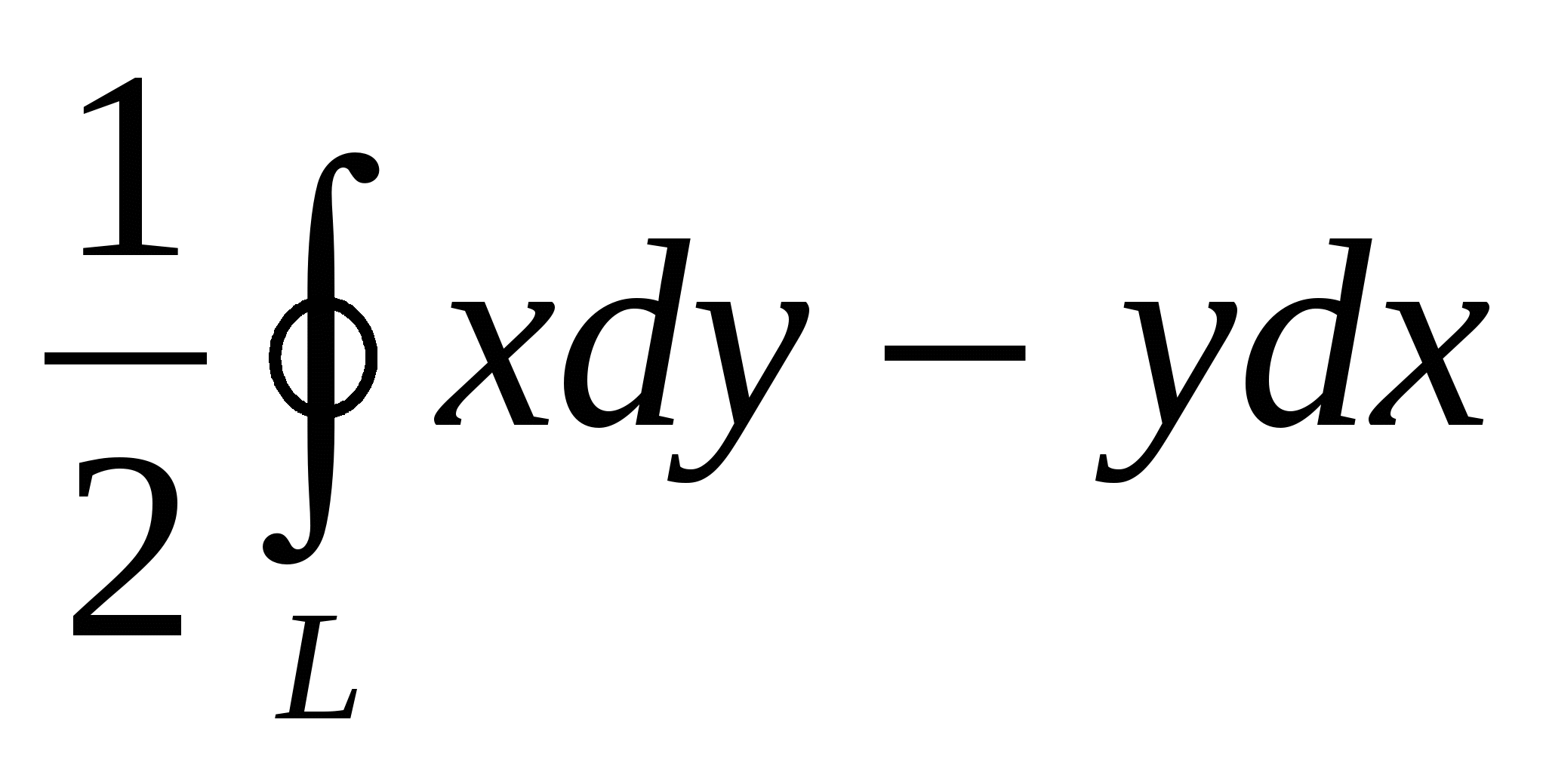 . .
|
5
|
Найти площадь четверти эллипса, заданного в параметрическом виде:
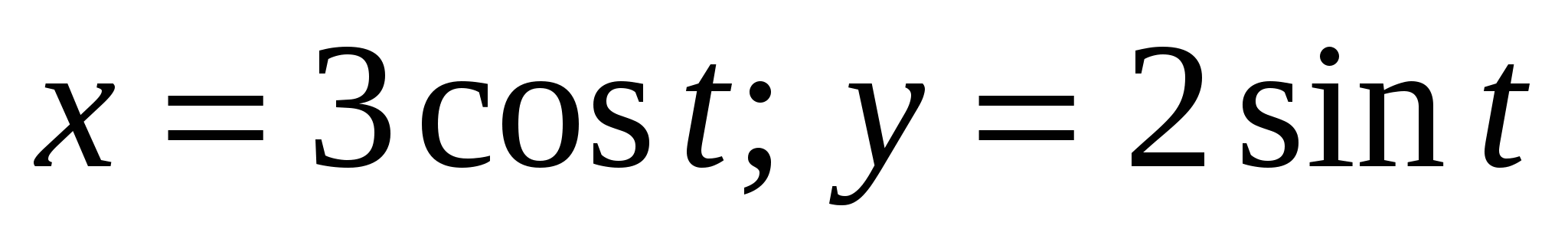 . .
|
1. 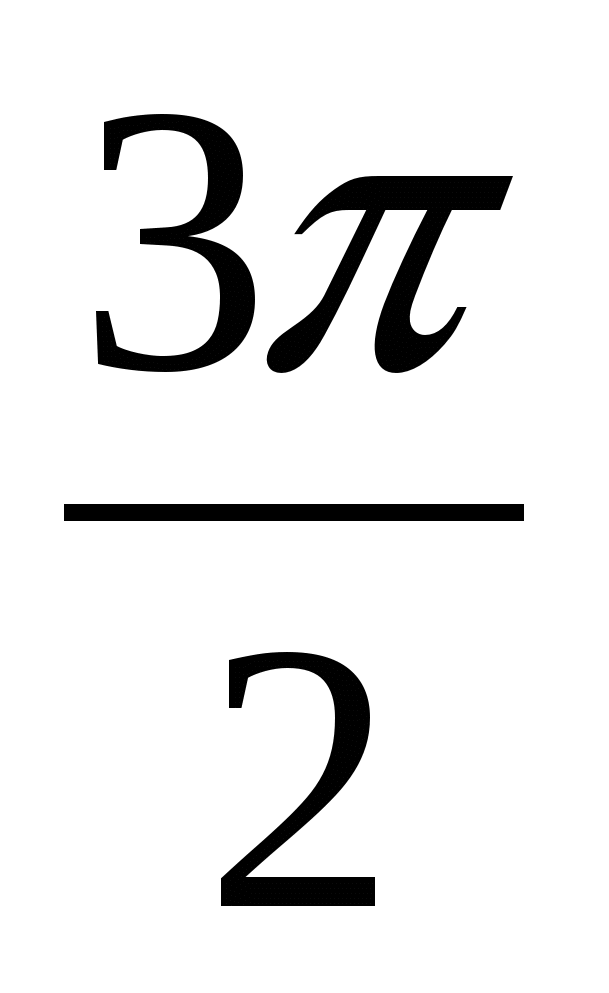 ; ;
2. 6π;
3. 6;
4. 1.
|
6
|
Укажите достаточные условия существования криволинейных интегралов 2 рода 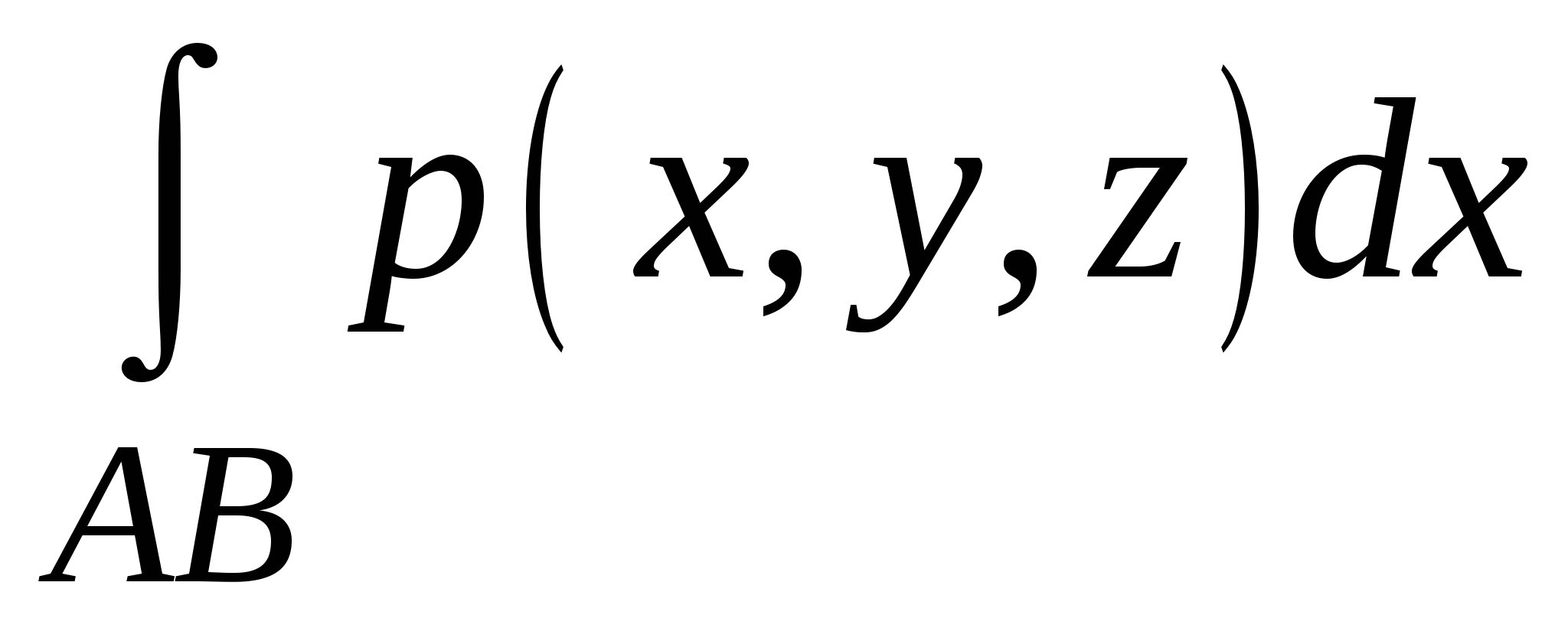 , , 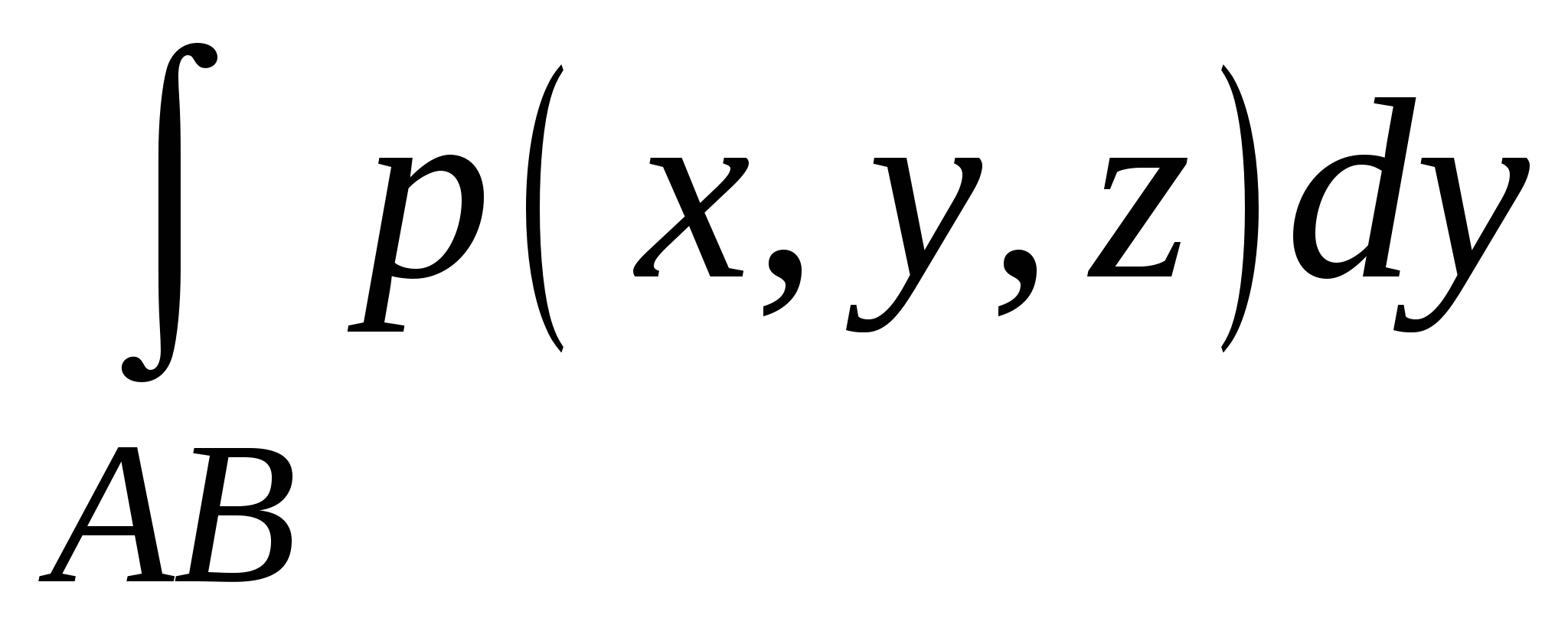 , , 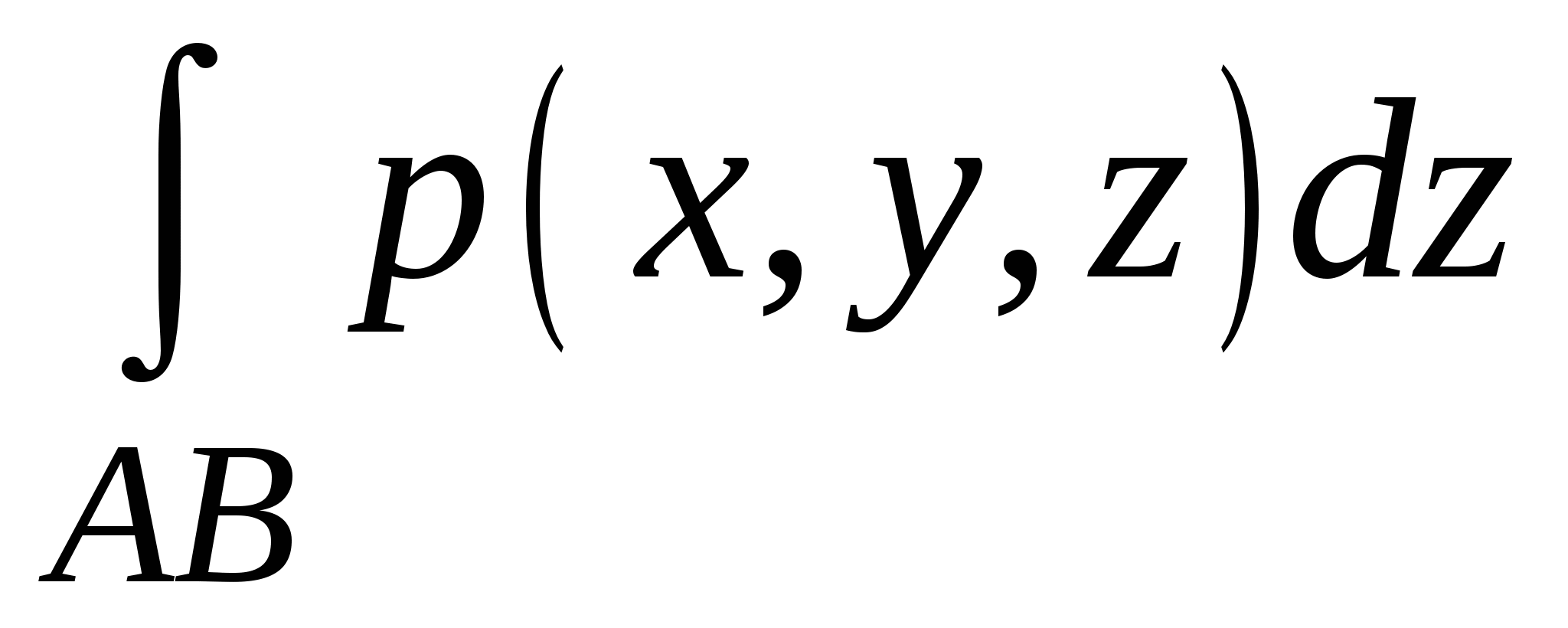 . .
|
1. Кривая 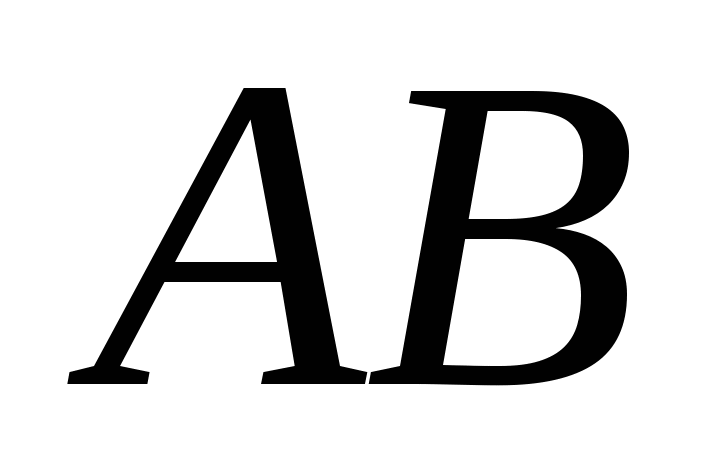 - плоская кривая; - плоская кривая;
2. Кривая 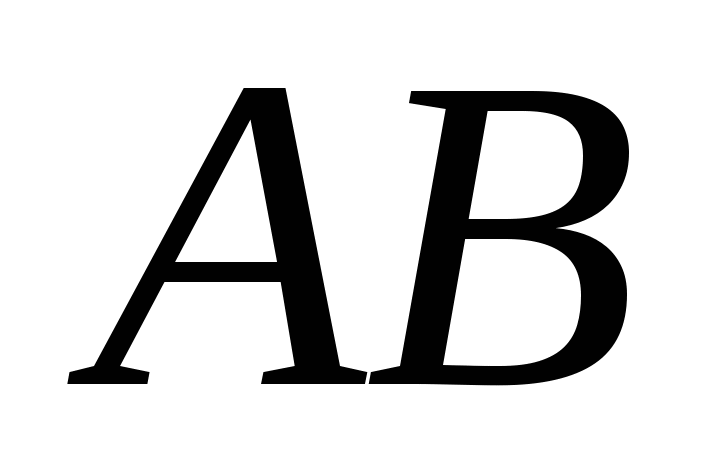 - кусочно-гладкая, а - кусочно-гладкая, а 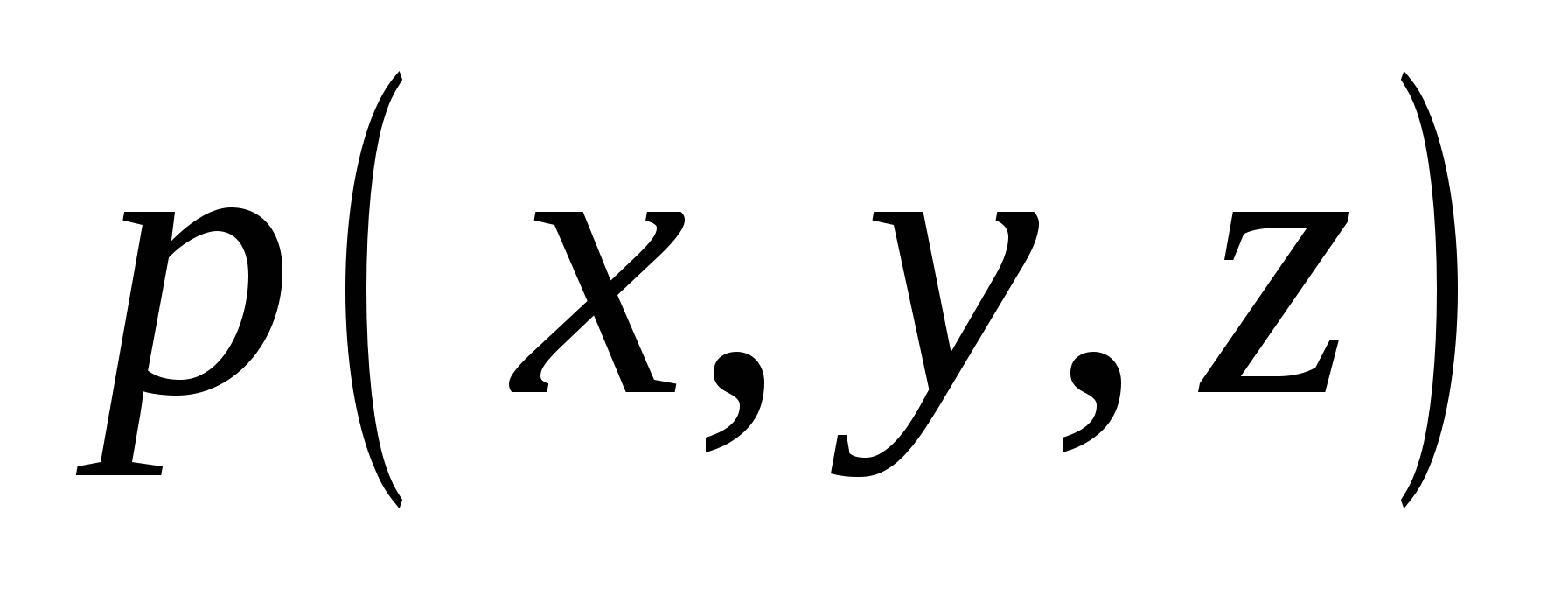 непрерывна на ней; непрерывна на ней;
3. Функция 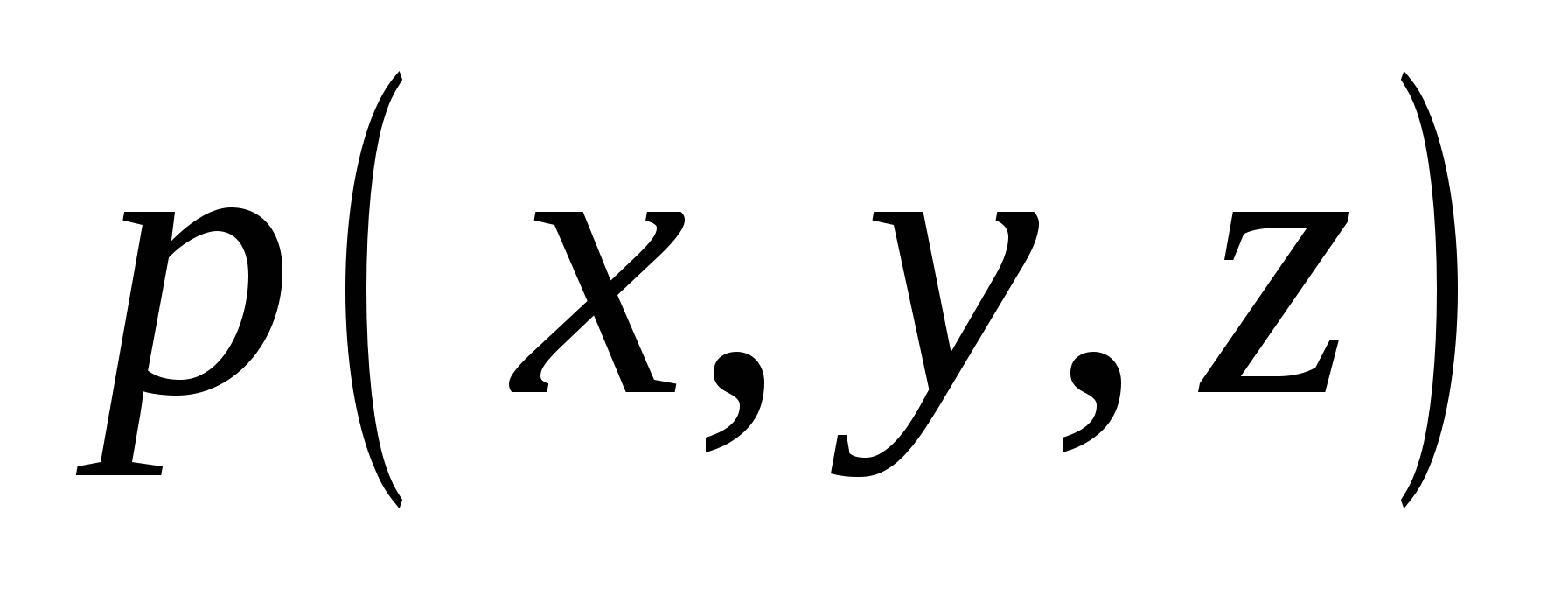 имеет на имеет на 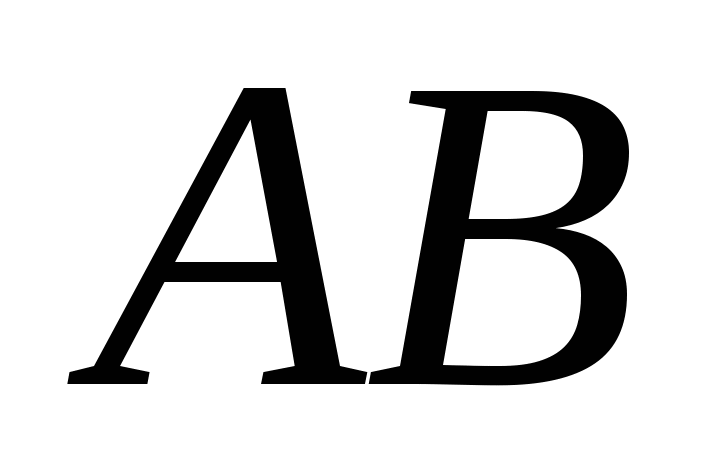 точки разрыва 1 рода; точки разрыва 1 рода;
4. Функция 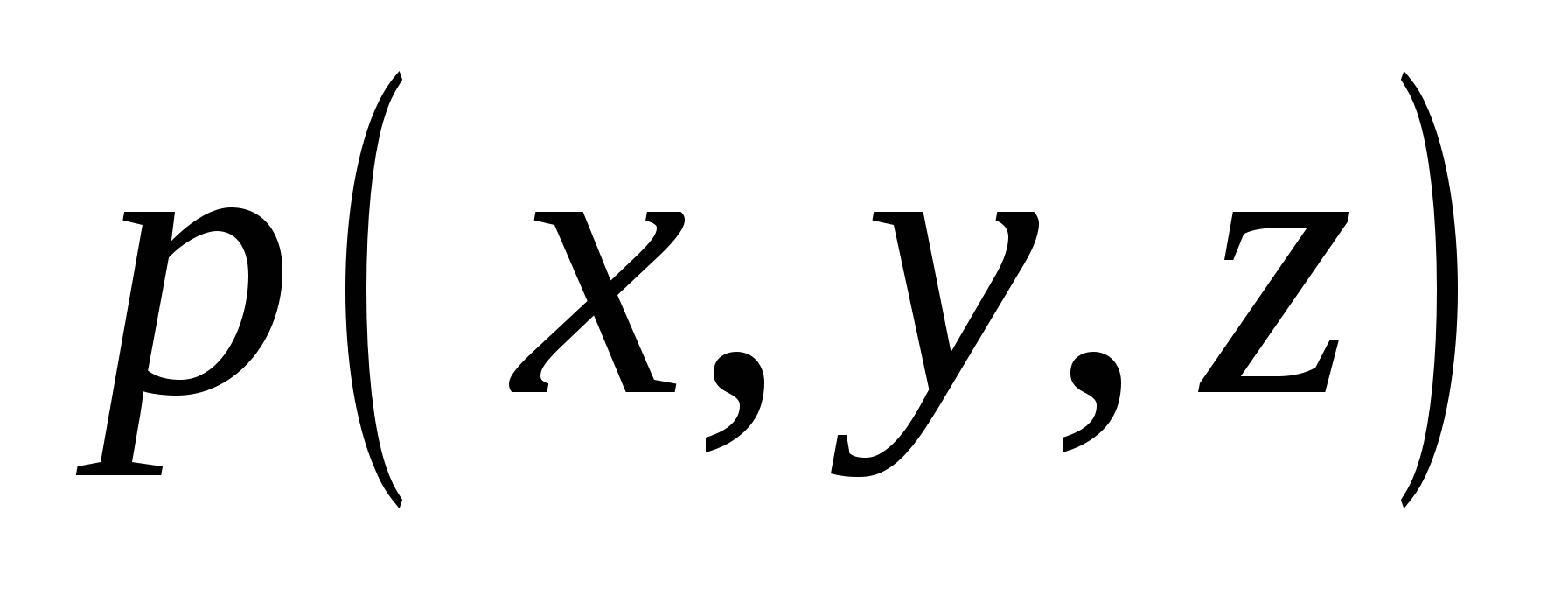 имеет на имеет на 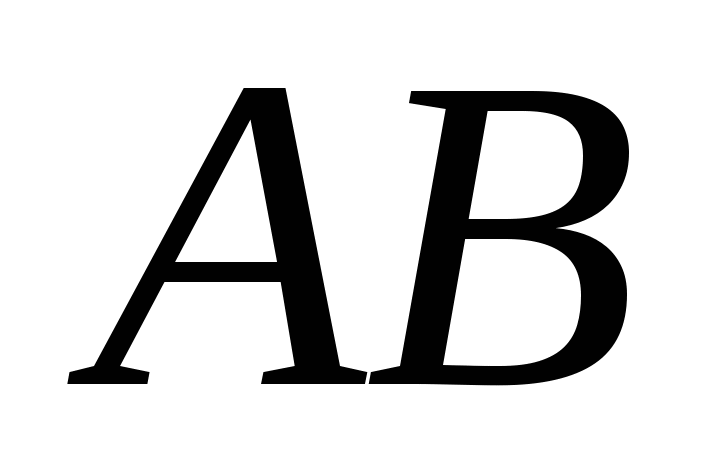 точки разрыва 2 рода. точки разрыва 2 рода.
|
7
|
Для интеграла
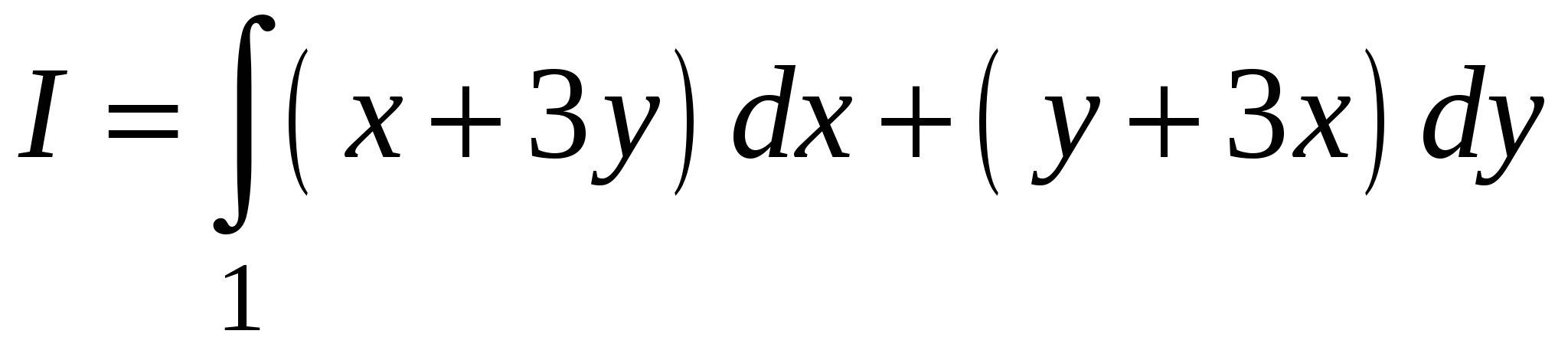
проверить выполнение условий
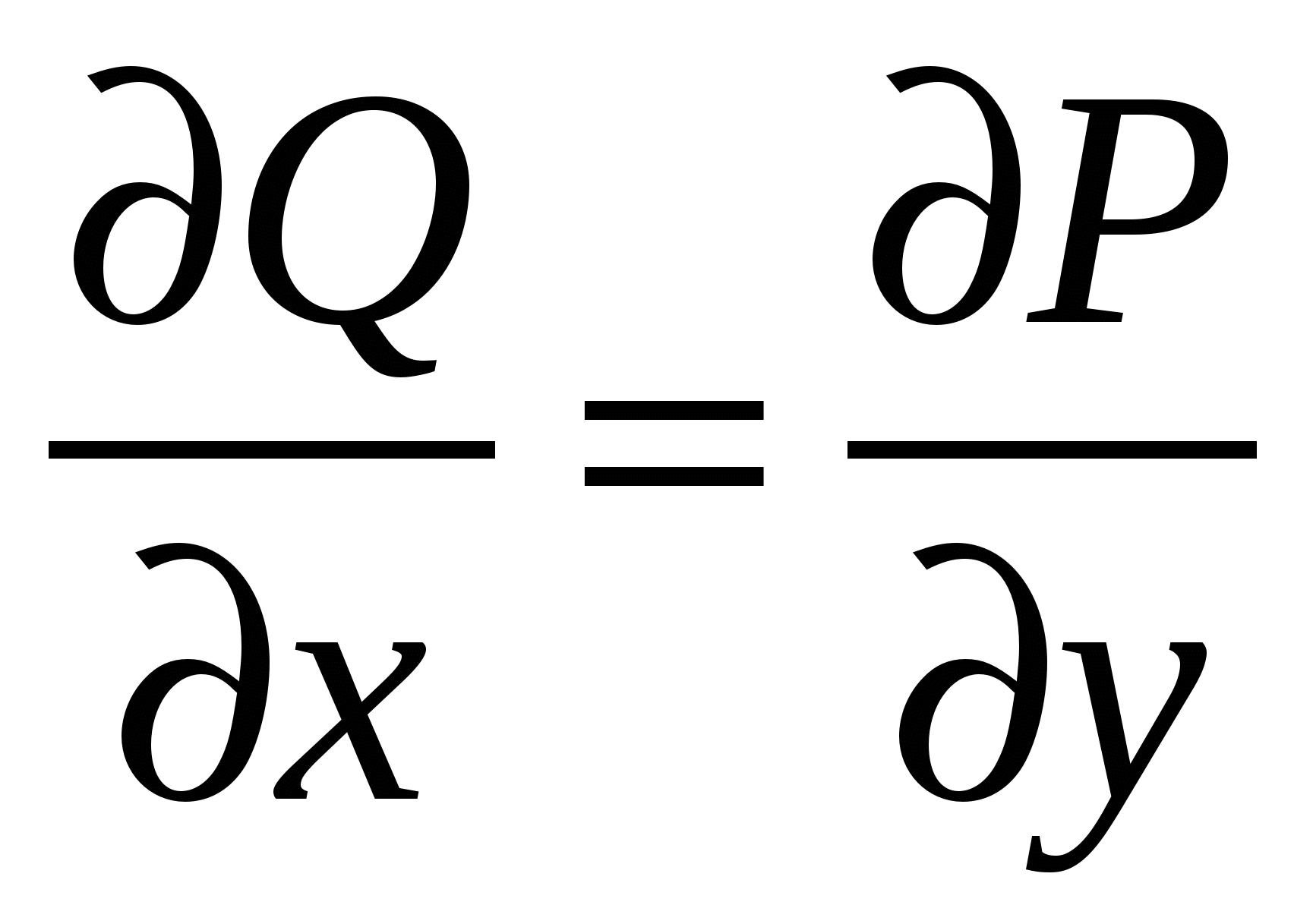 . .
|
1. Условия не выполняются;
2. Функции P не существует;
3. Функции Q не существует;
4. Условия выполняются.
|
8
|
Вычислите интеграл 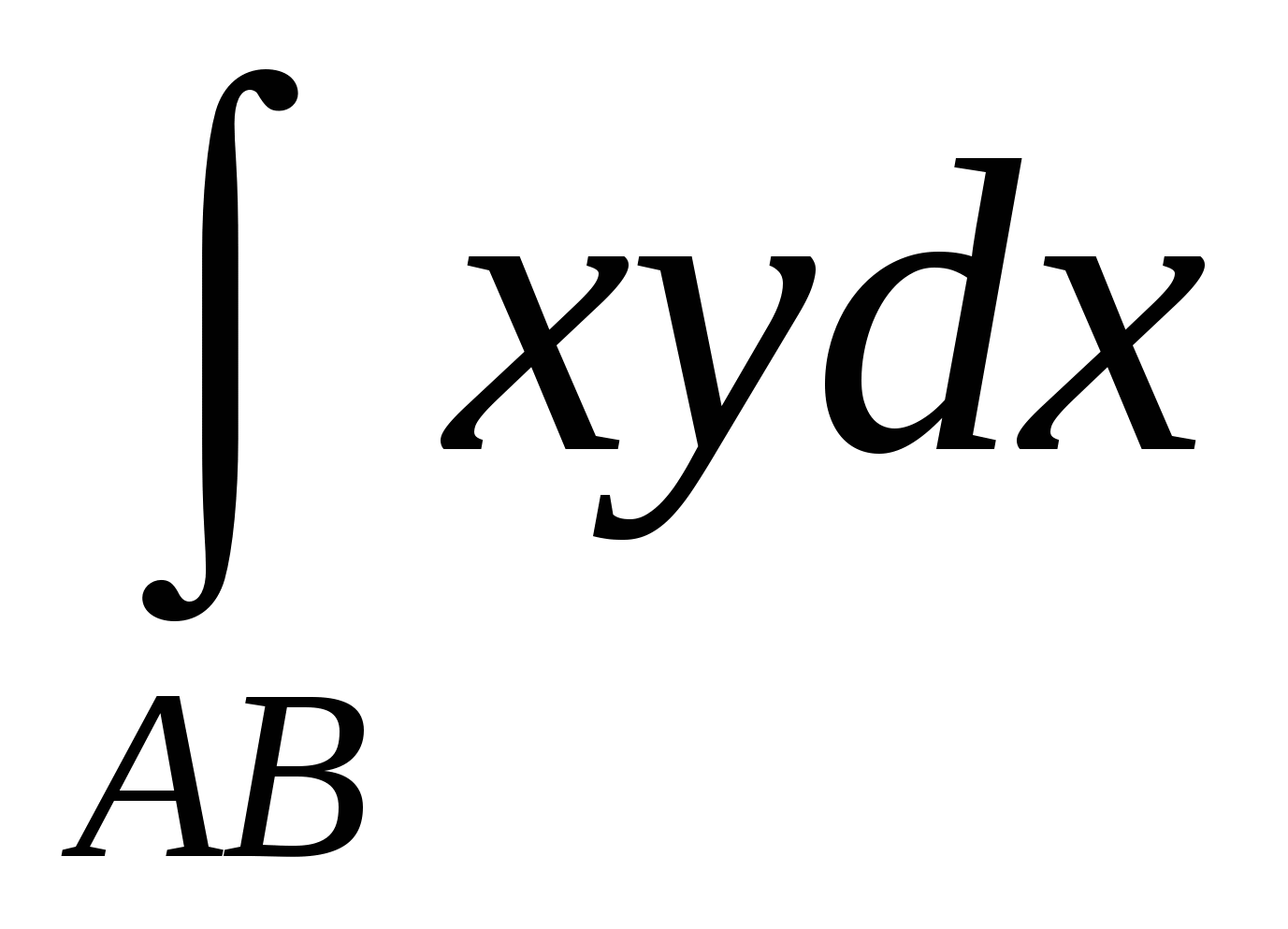 по кривой по кривой 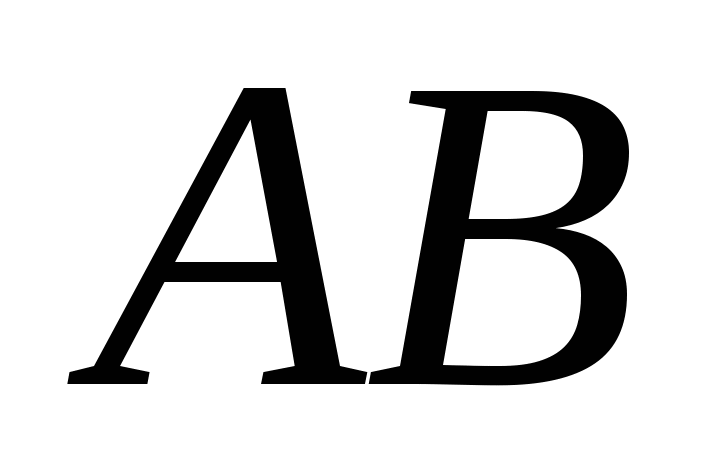 , описанной уравнением , описанной уравнением 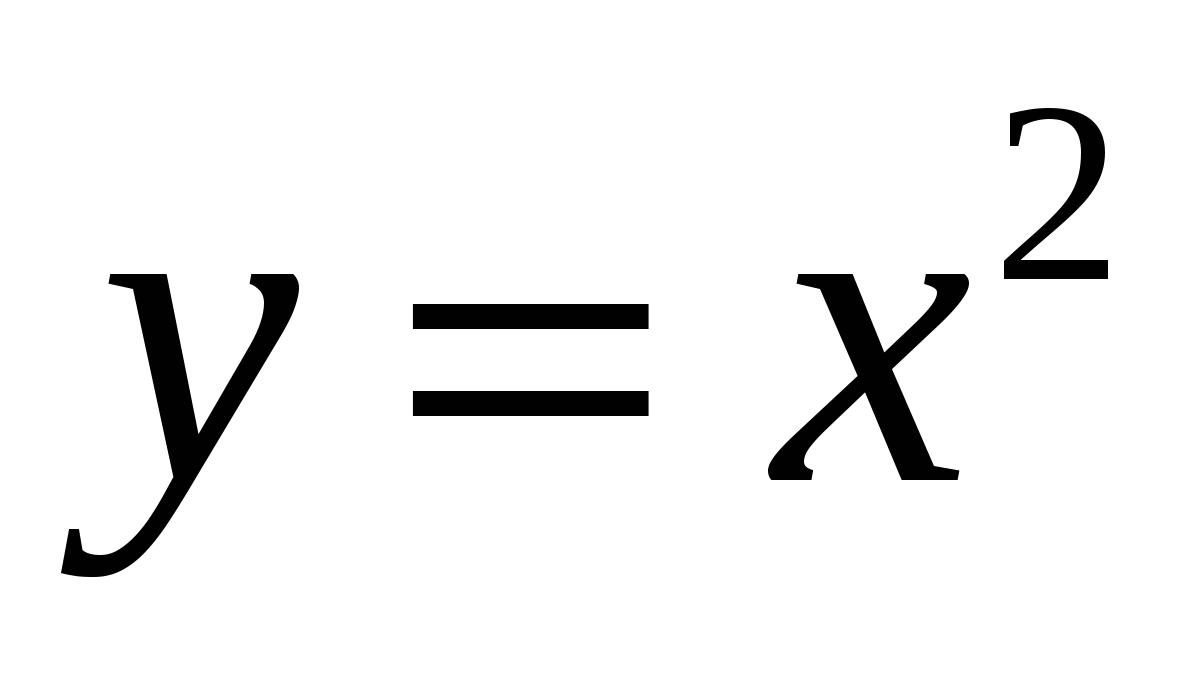 от точки от точки 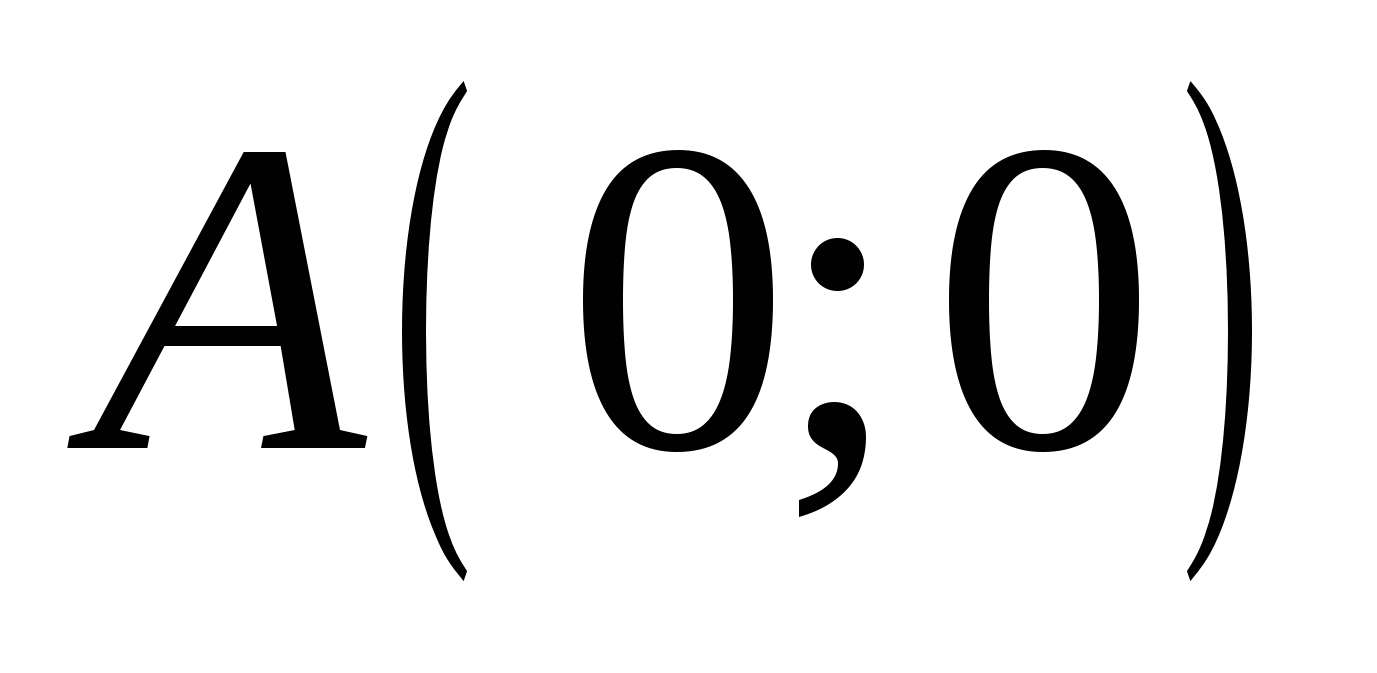 до до 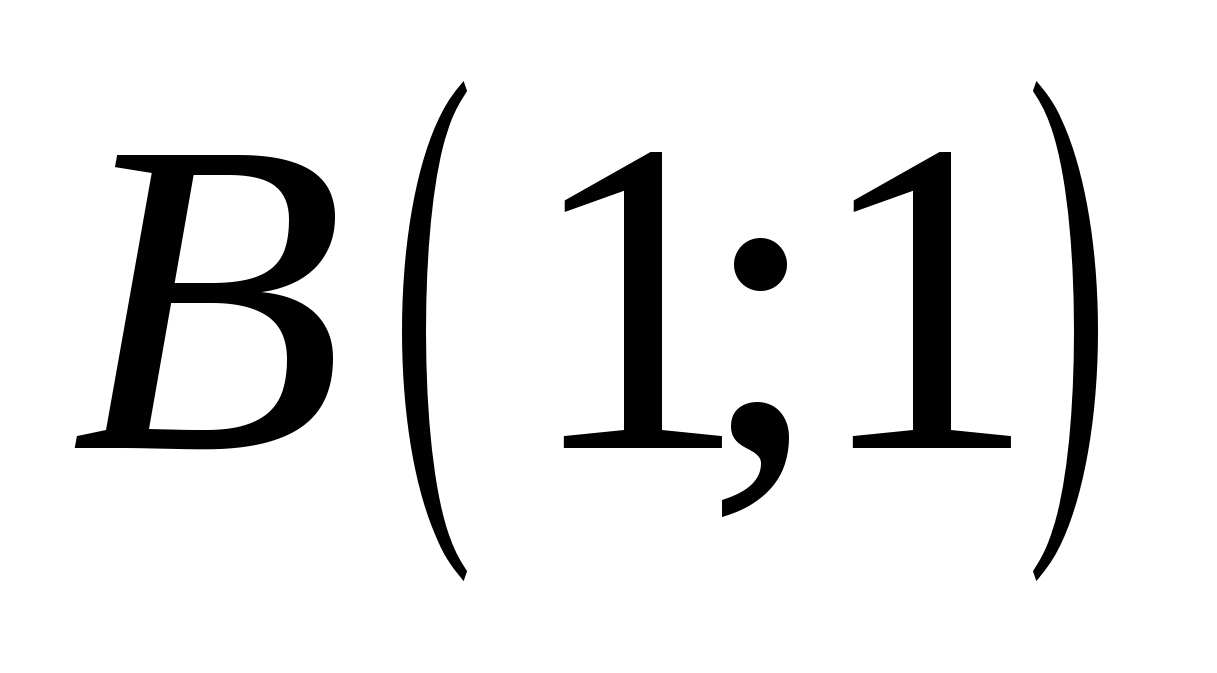 . .
|
1. 2;
2. 3;
3. 1;
4. 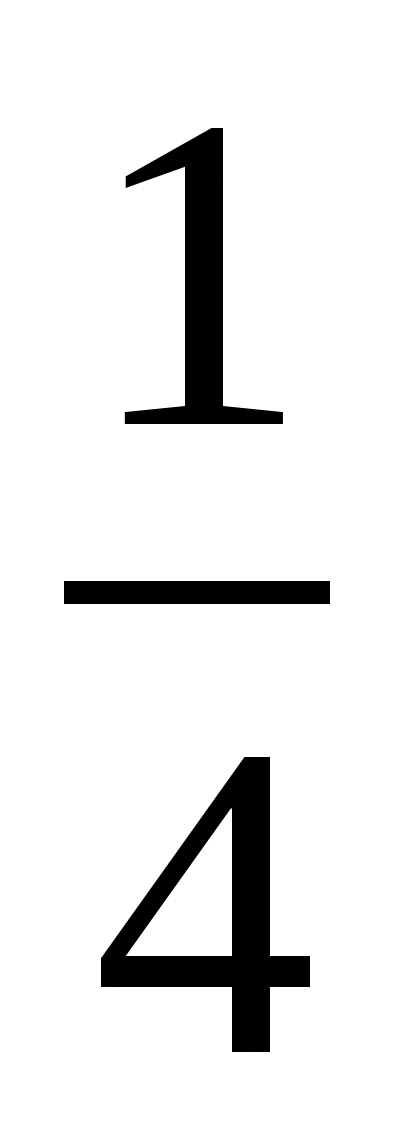 . .
|
9
|
Для непрерывных функций P, Q, 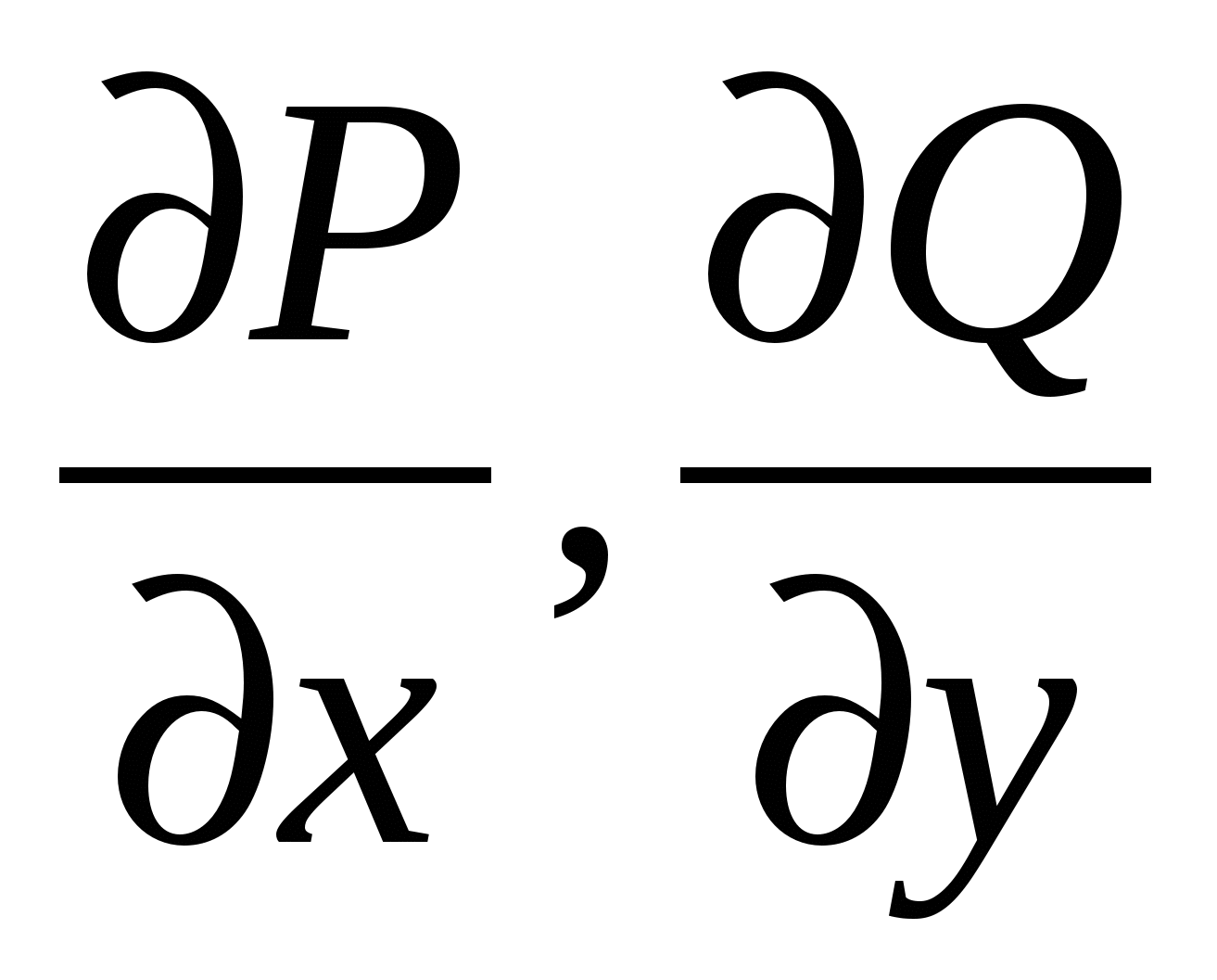 в области D, имеющей кусочно-гладкую границу L, формула Грина имеет вид: в области D, имеющей кусочно-гладкую границу L, формула Грина имеет вид:
|
1. 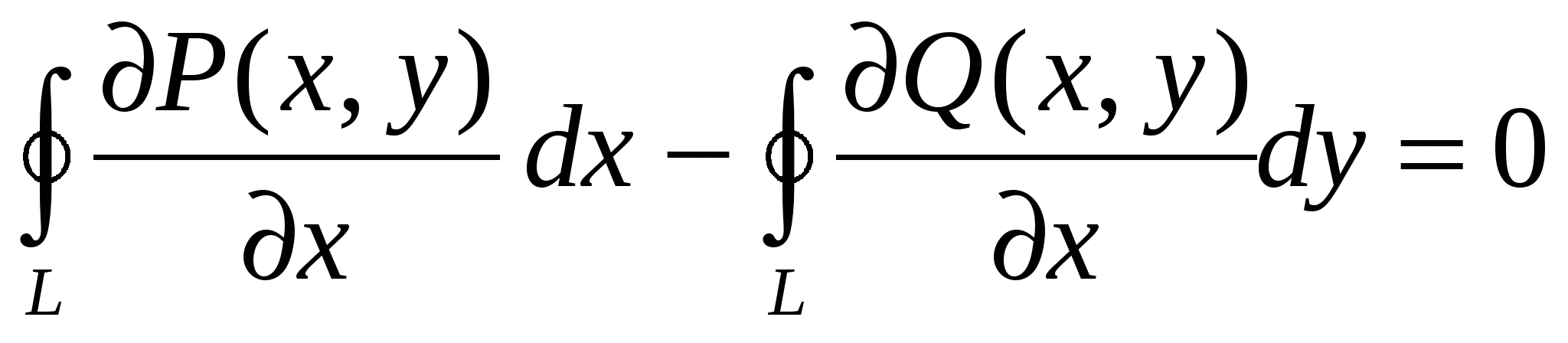 ; ;
2.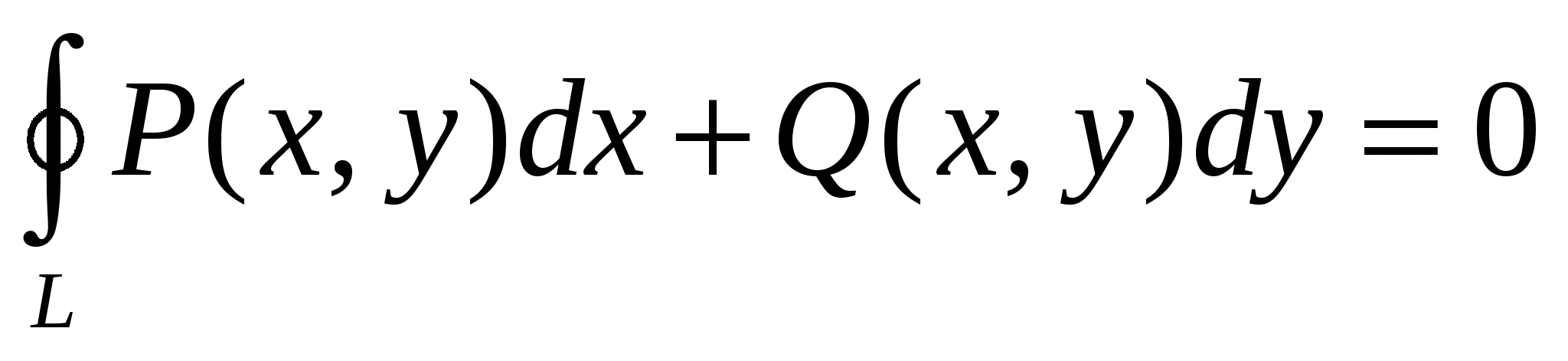 ; ;
3. 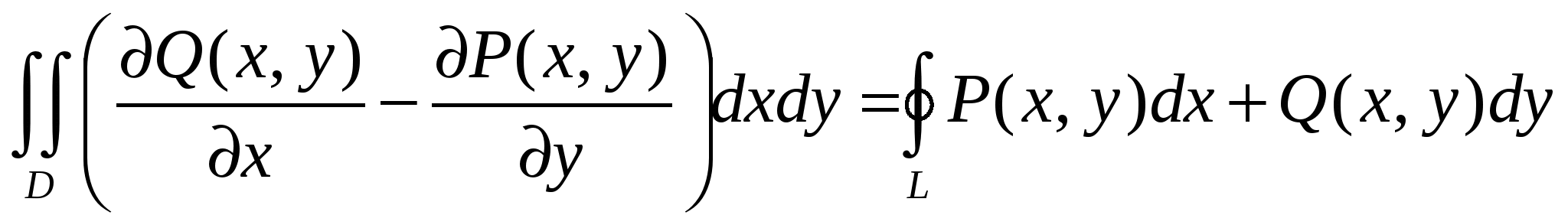
4.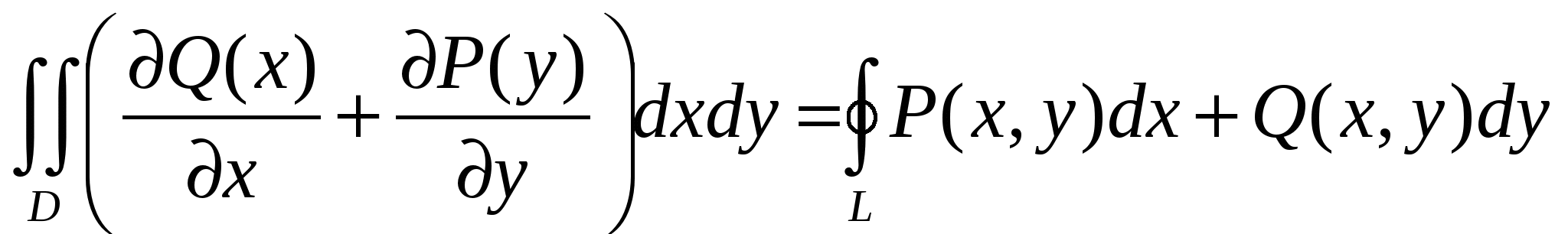
|
10
|
Вычислить интеграл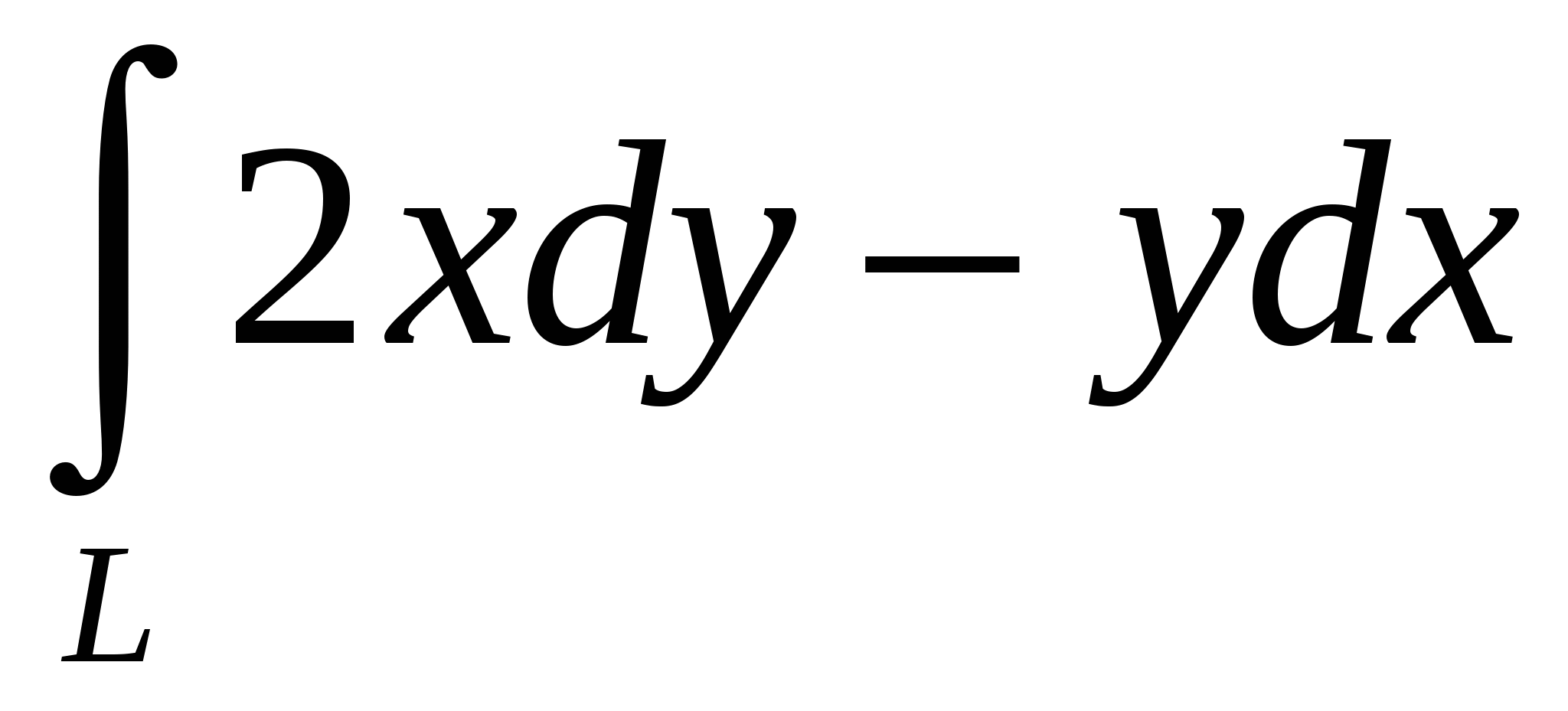 по отрезку прямой по отрезку прямой 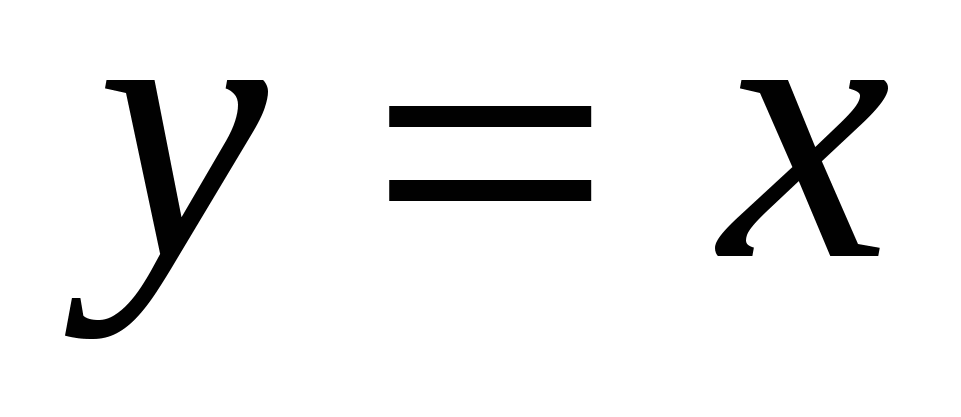 от точки от точки 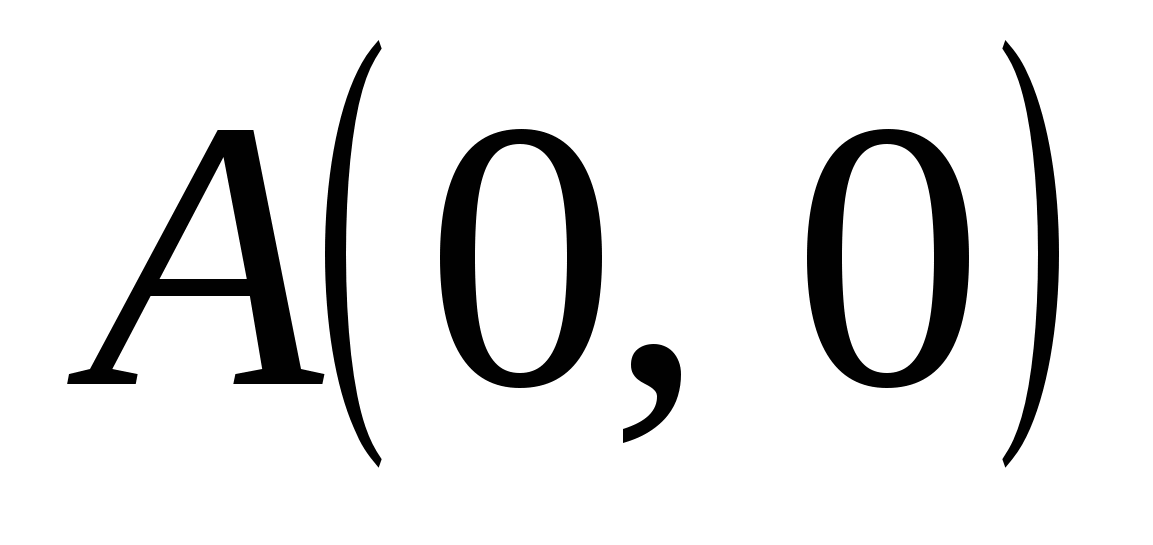 до точки до точки 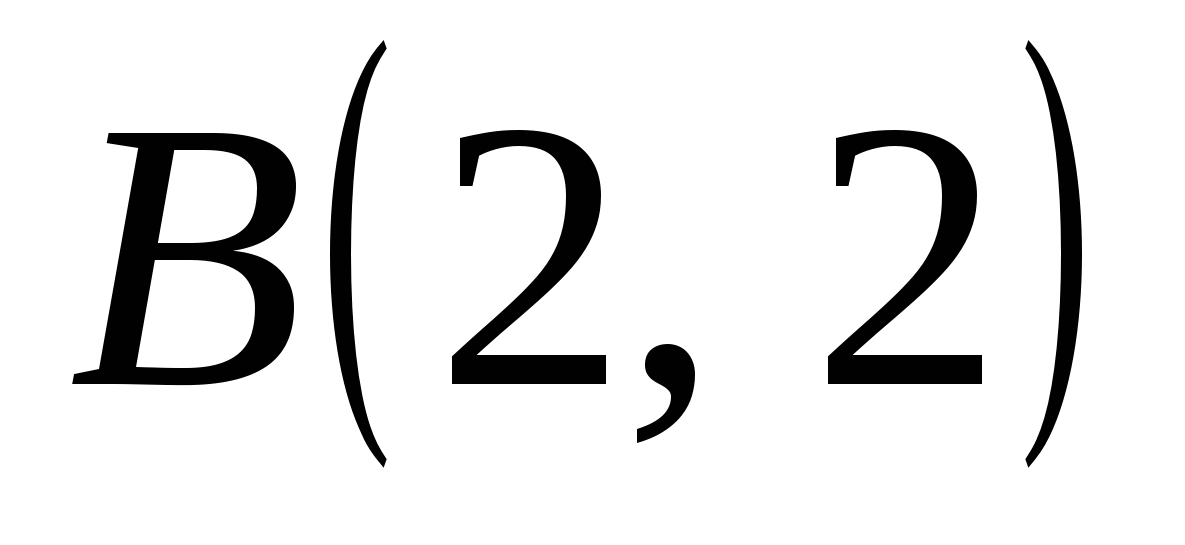 . .
|
1. 2;
2. -1 ;
3. -4 ;
4. -2 ;
|
11
|
Укажите условия независимости криволинейного интеграла 2 рода
от пути интегрирования
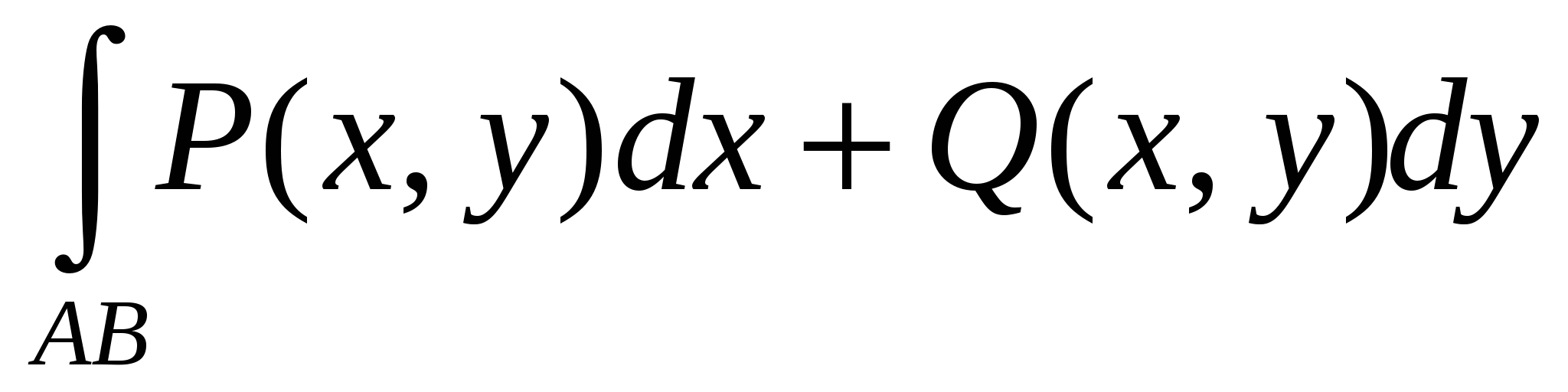
|
1. 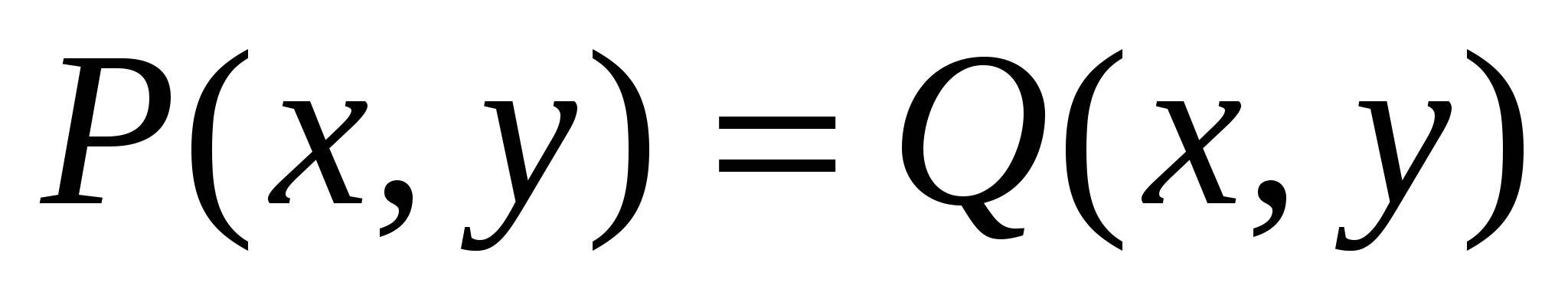 ; ;
2. 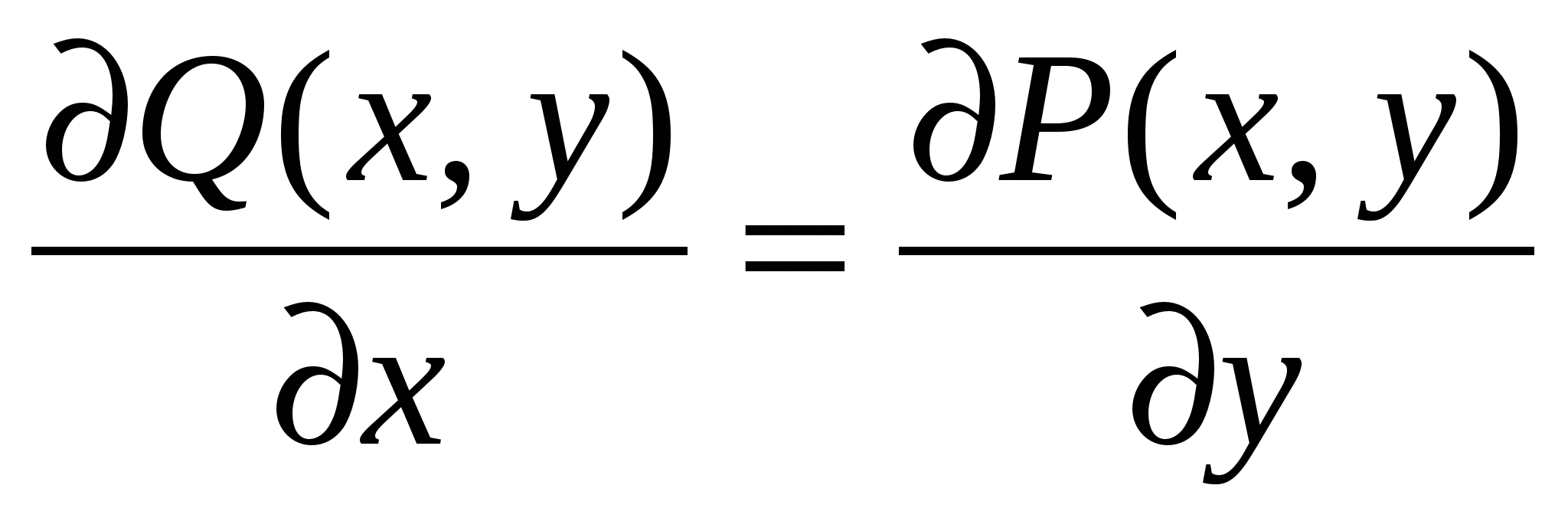 ; ;
3. 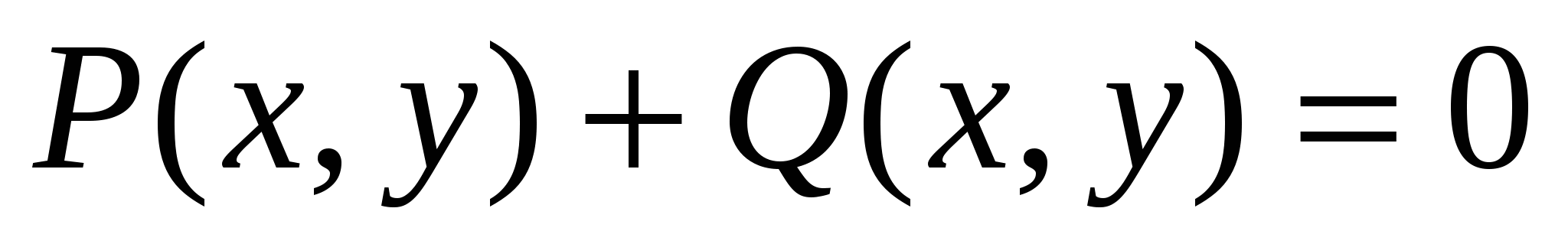 ; ;
4. 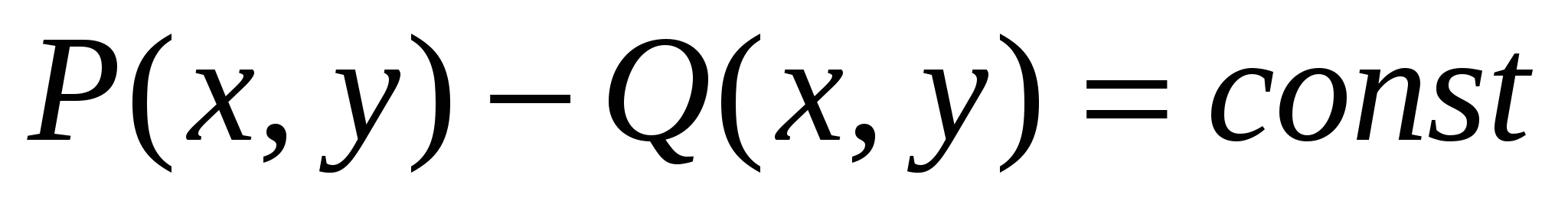 . .
|
12
|
Найти 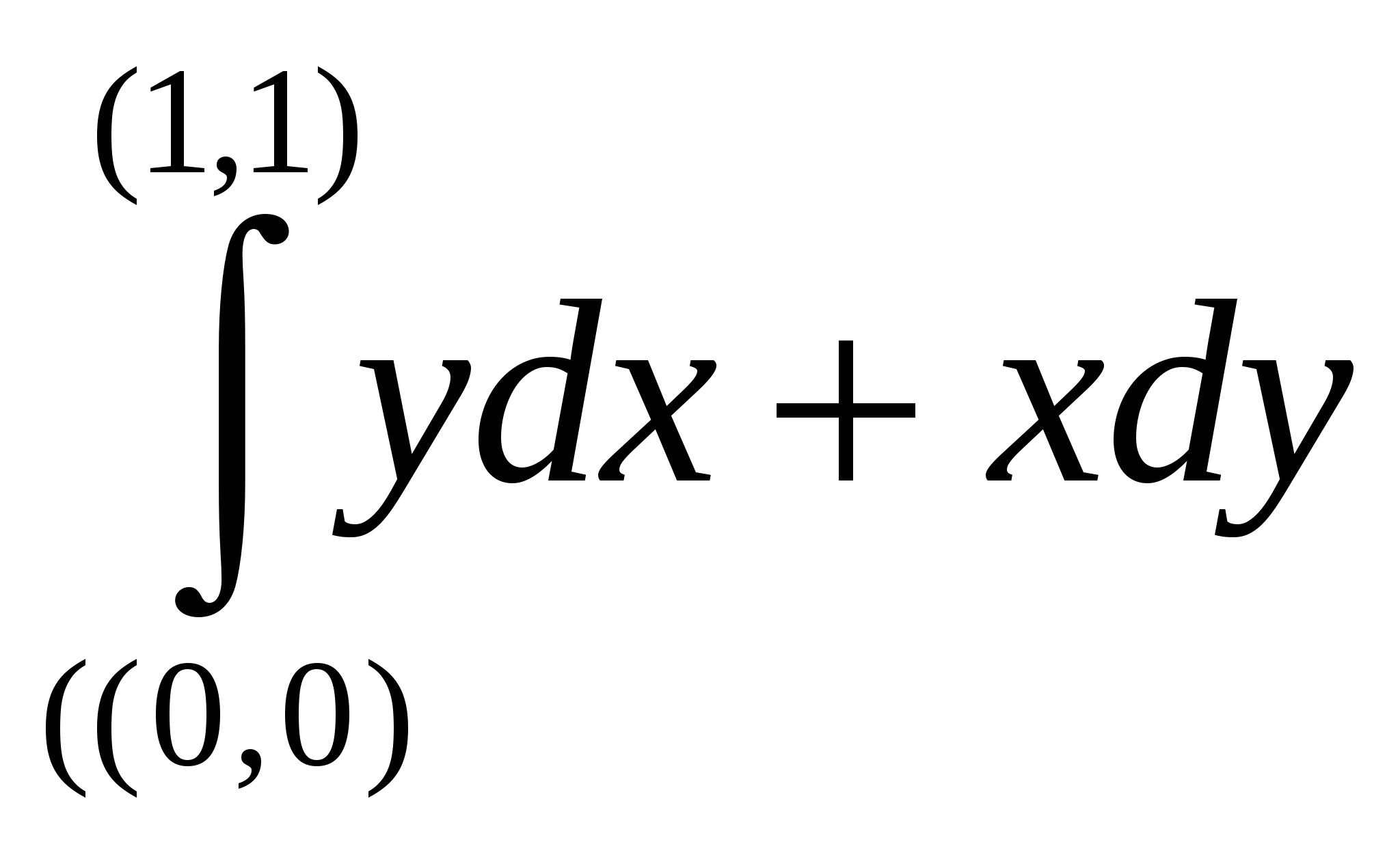 , используя условия независимости криволинейного интеграла от пути интегрирования. , используя условия независимости криволинейного интеграла от пути интегрирования.
|
1. 2;
2. 3;
3. 1;
4. 0.
|
13
|
При изменении направления пути интегрирования, криволинейный интеграл 2 рода равен:
|
1. 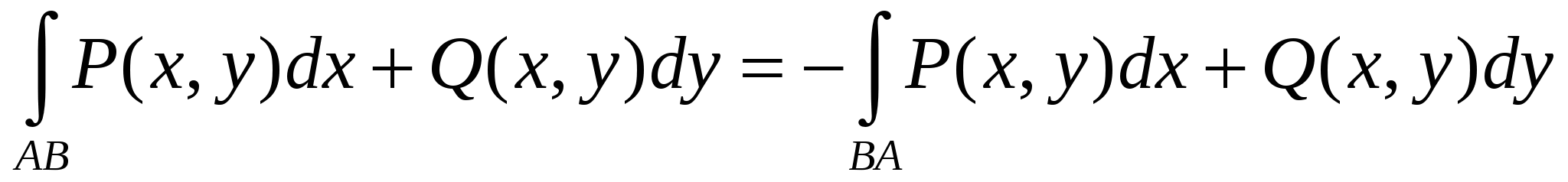 . .
2. 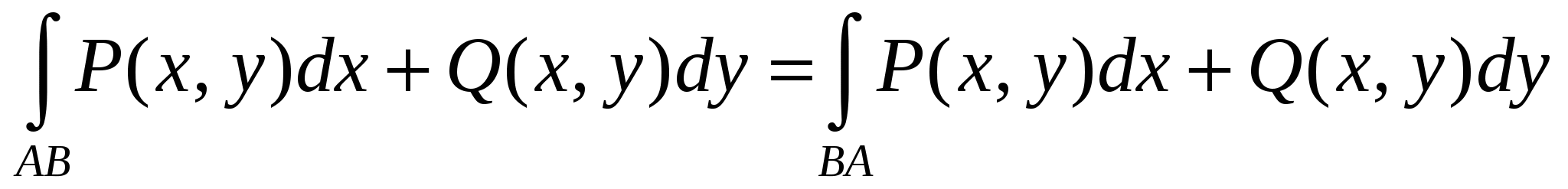 . .
3. 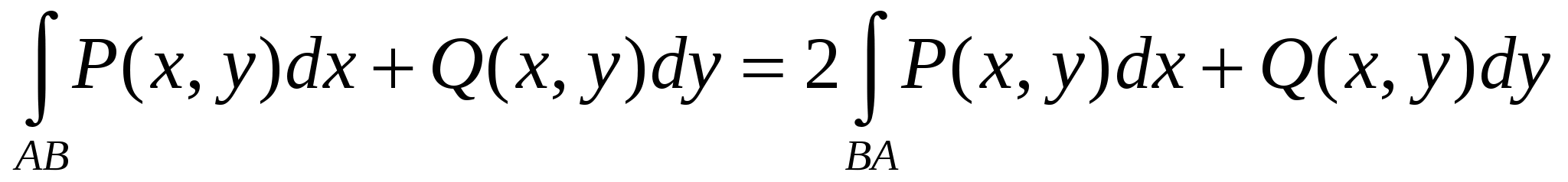 . .
4. 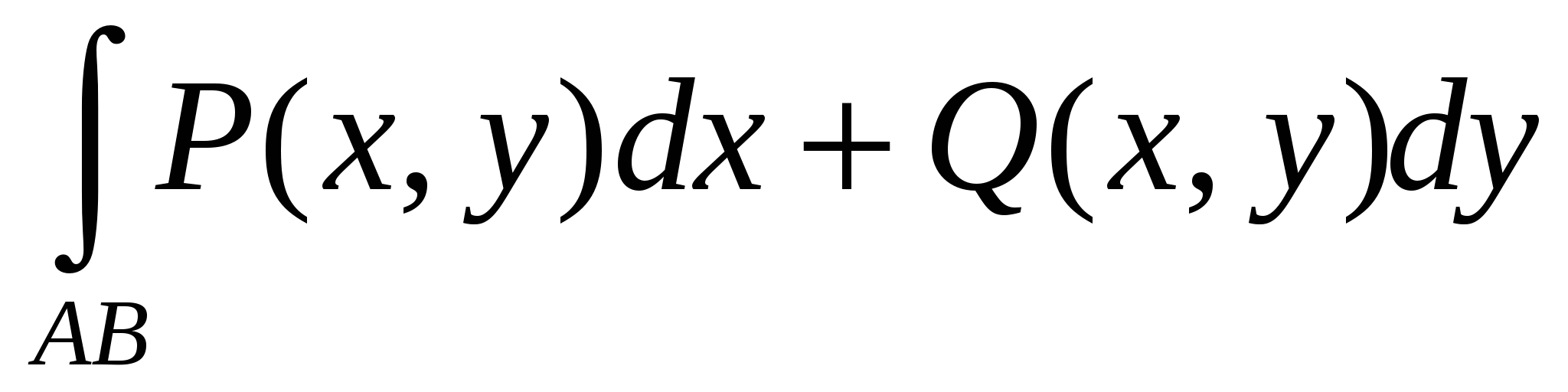 =0. =0.
|
14
|
Применяя формулу Грина вычислить криволинейный интеграл 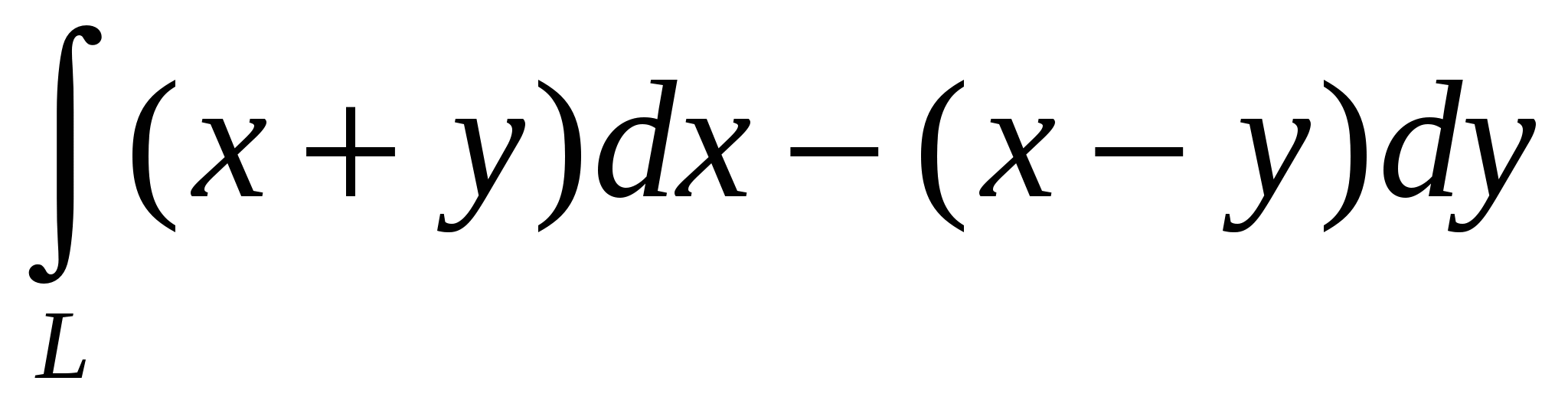 , где L-окружность: , где L-окружность: 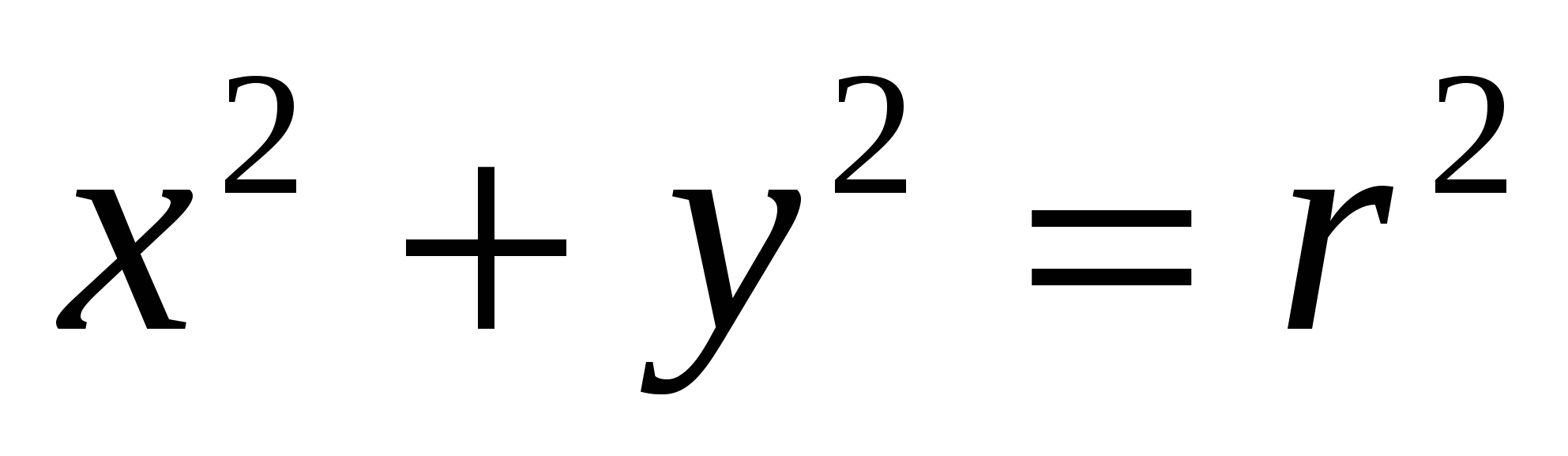 . .
|
1. r2;
2. 4;
3. πr;
4. -2πr2.
|
15
|
Если 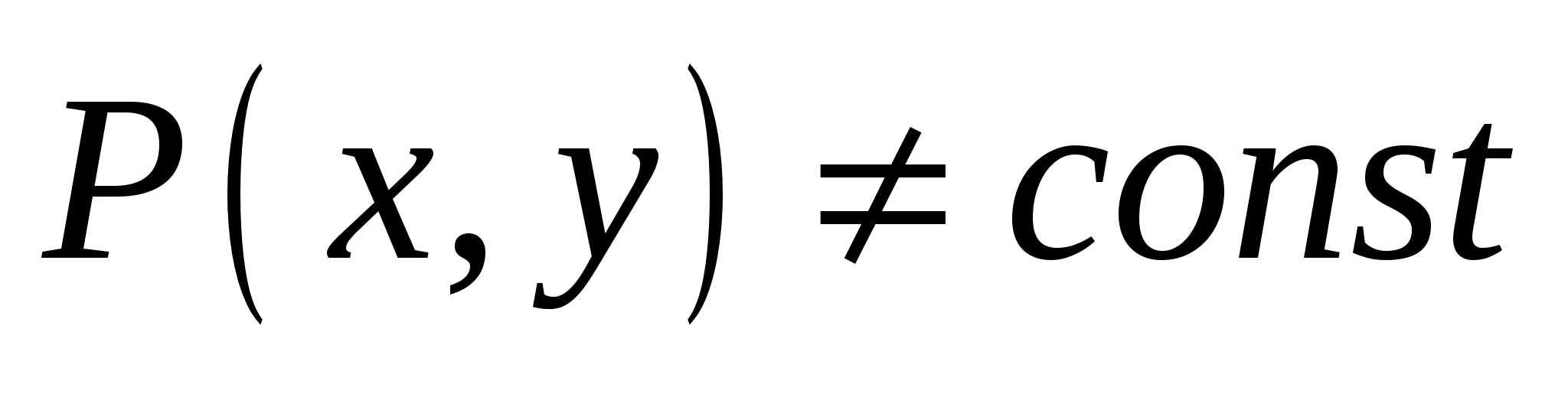 и и 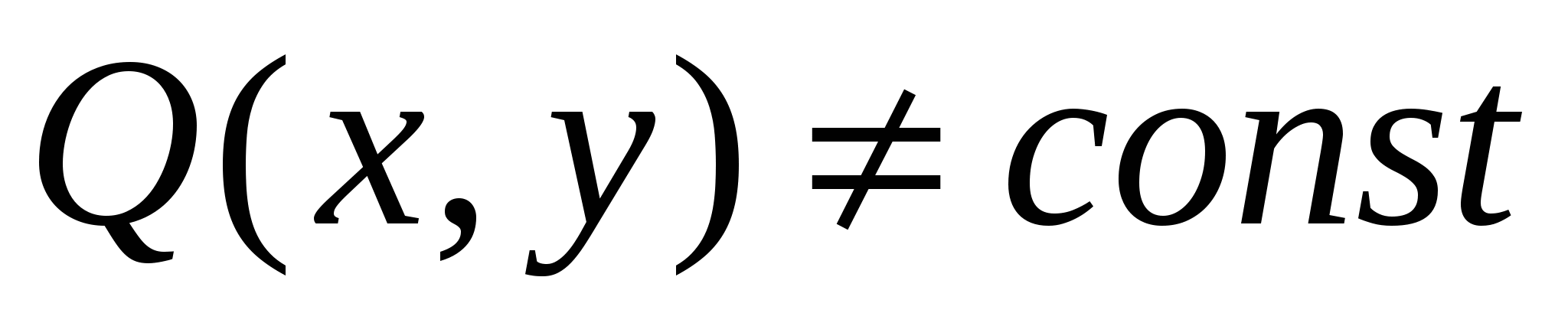 , то криволинейный интеграл второго рода , то криволинейный интеграл второго рода 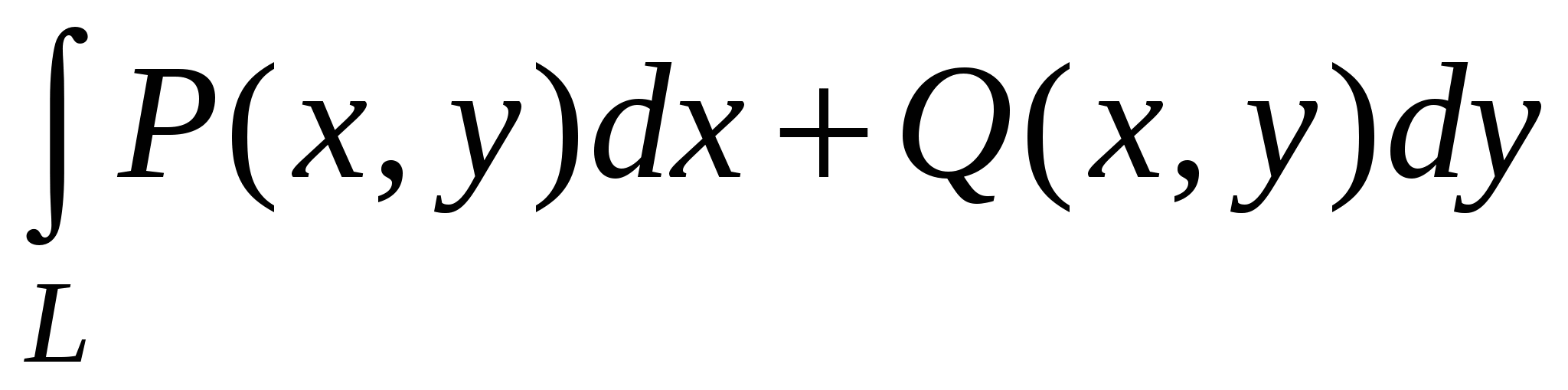 равен: равен:
|
1.Массе дуги;
2.Длине контура  ; ;
3. Работе переменной силы 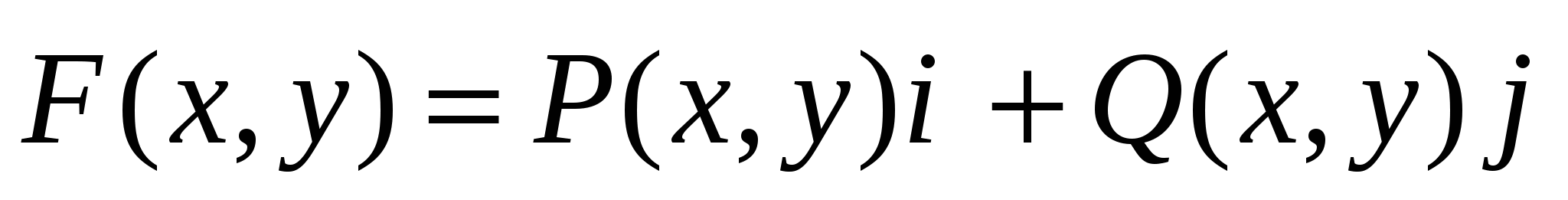
вдоль контура  , в заданном направлении; , в заданном направлении;
4. Работе постоянной силы 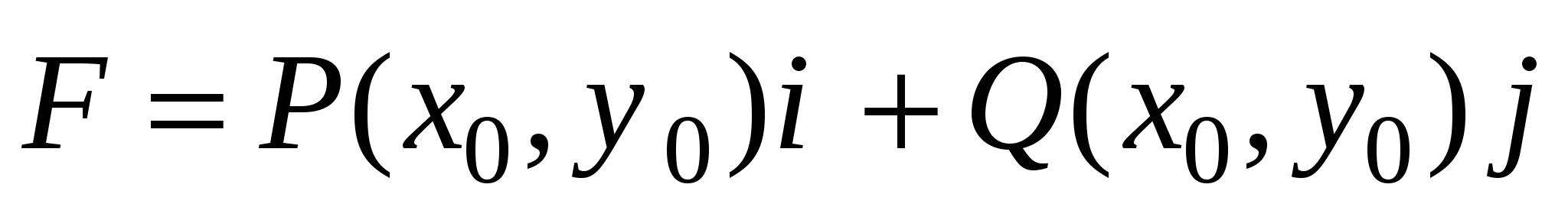 . .
|
16
|
Если кривая AB точкой С разбита на две части ACиCB, то интеграл равен:
|
1. 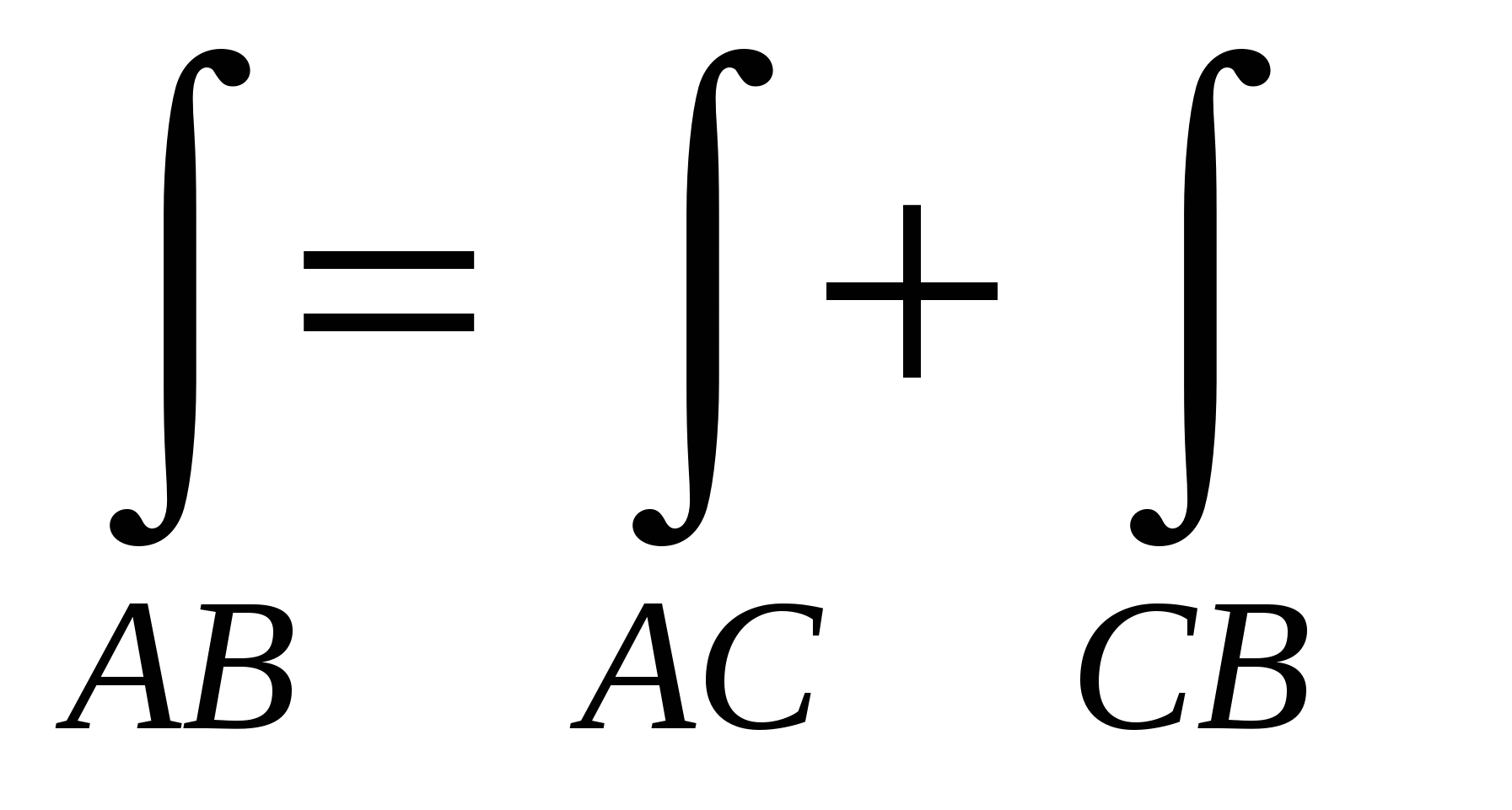 ; ;
2. 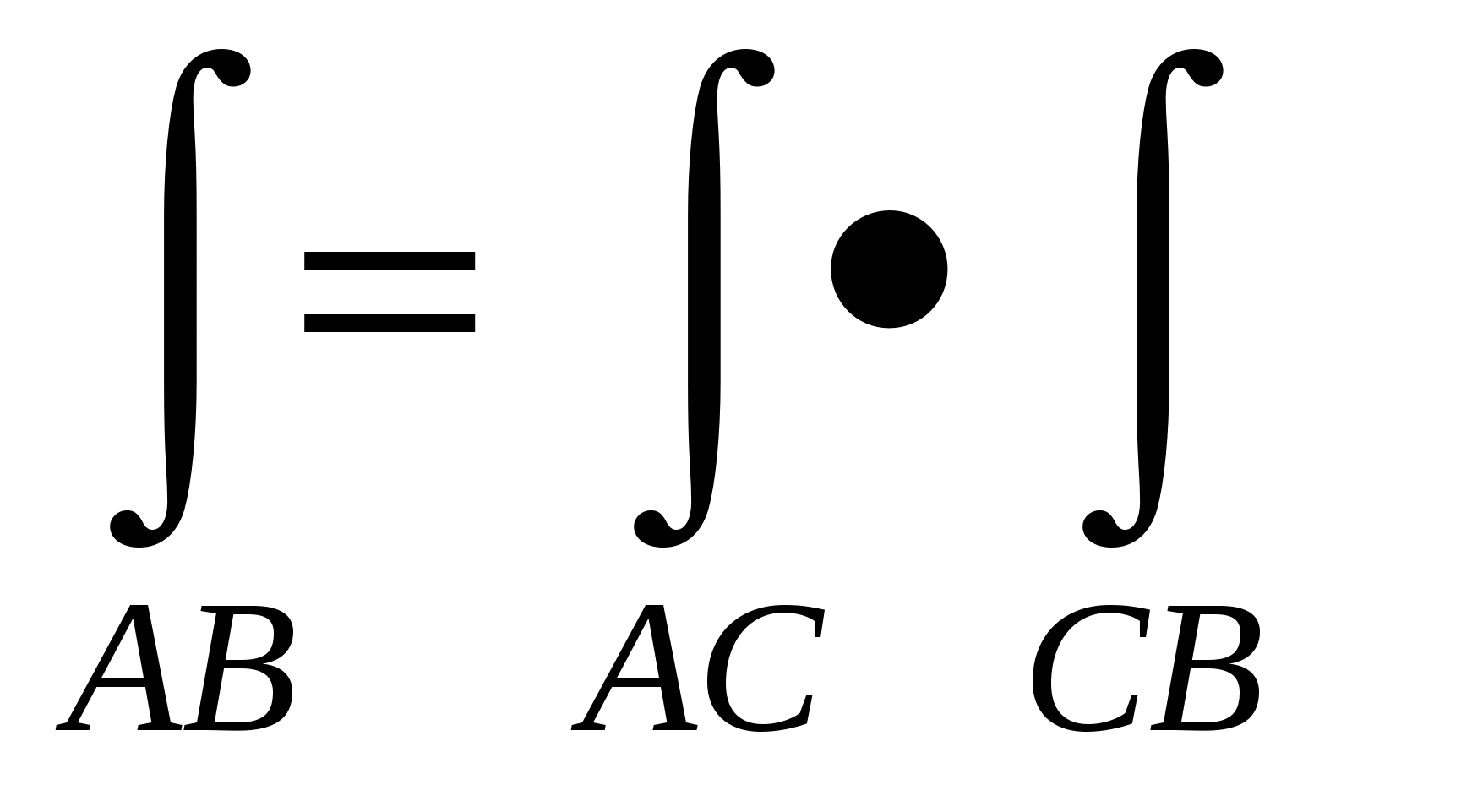 ; ;
3. 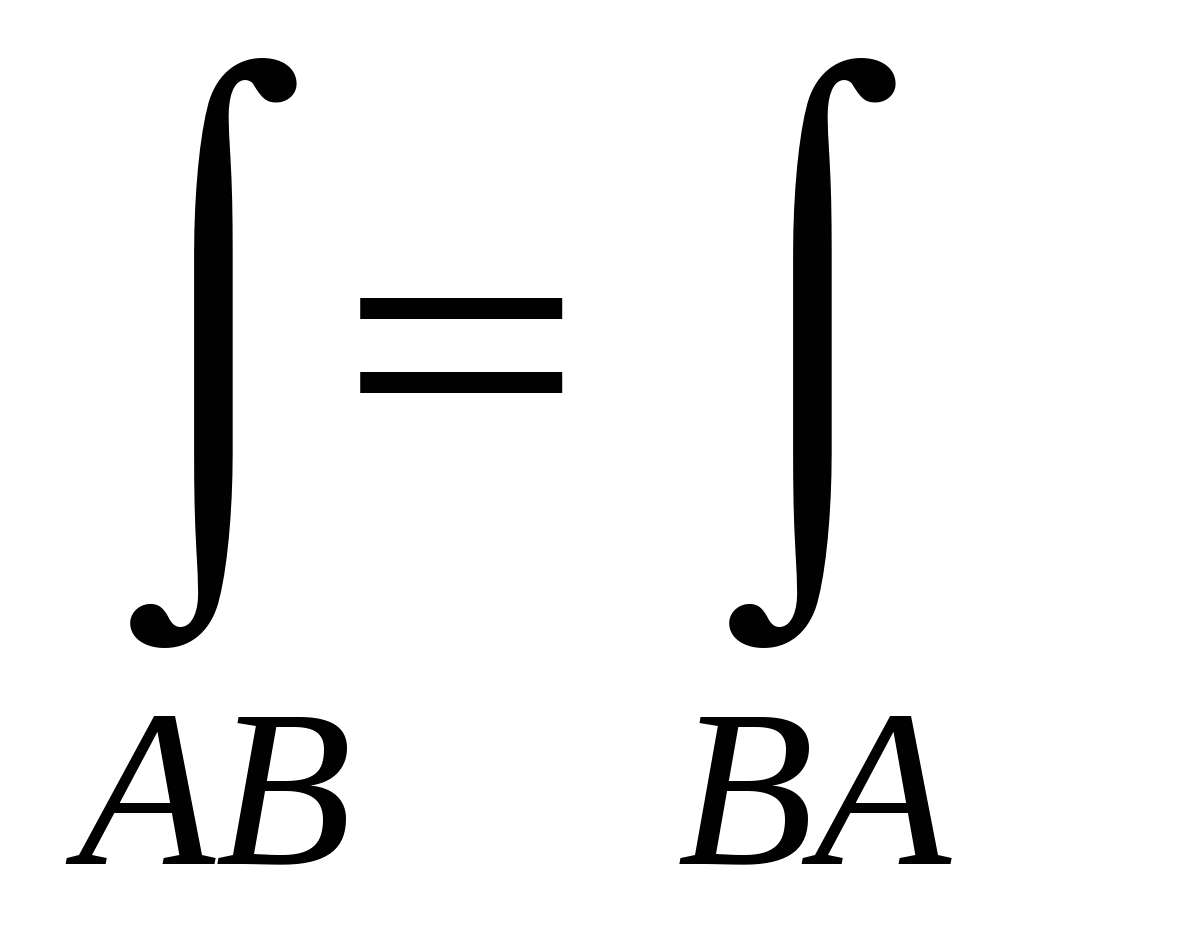 ; ;
4. 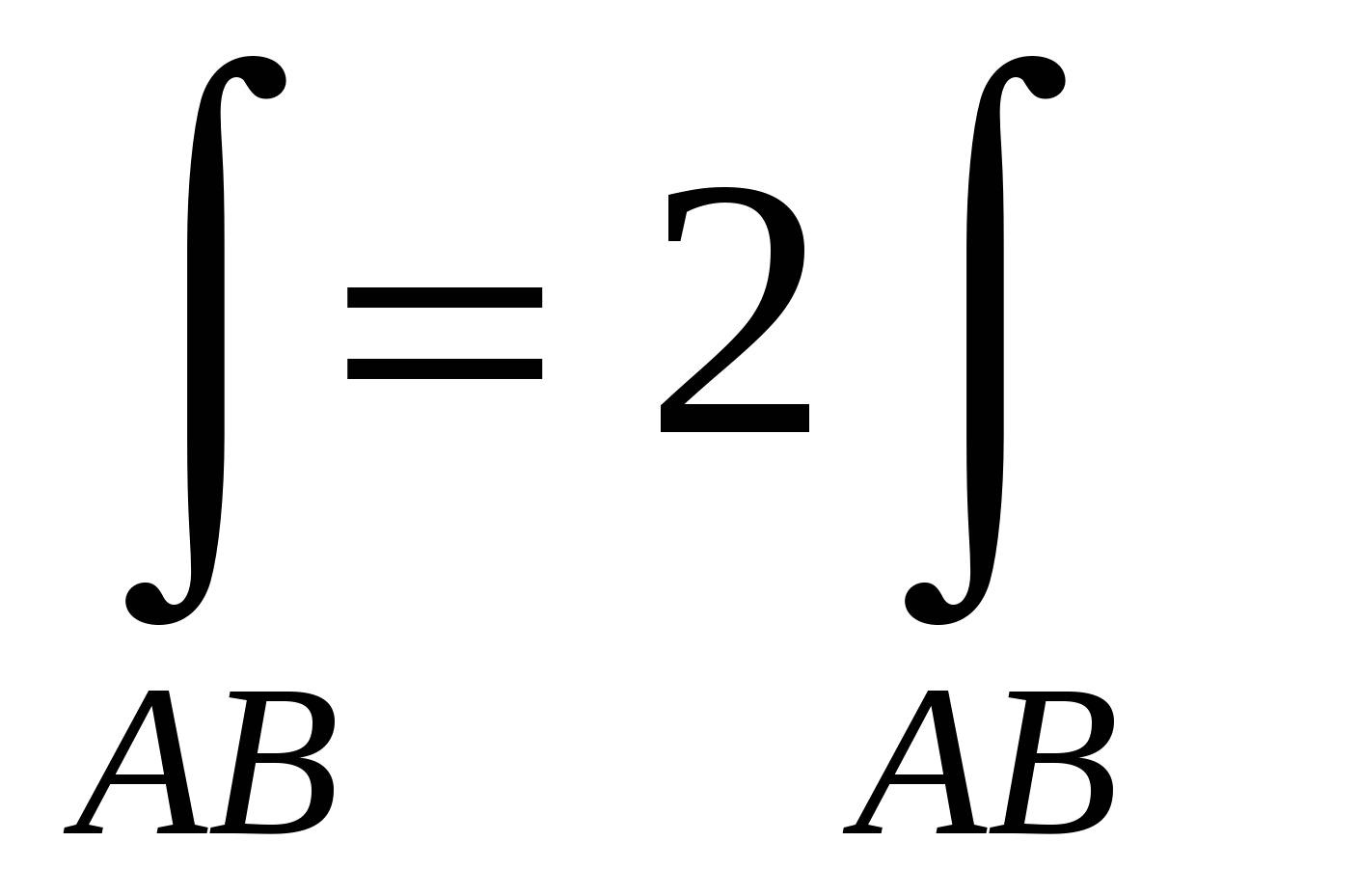 . .
|
17
|
Задача о вычислении работы переменной силы при перемещении материальной точки вдоль кривой ABприводит к понятию….
|
1. двойного интеграла;
2. криволинейного интеграла ІІ рода;
3. тройного интеграла;
4. массы дуги.
|
18
|
Вычислить с помощью формулы Грина интеграл
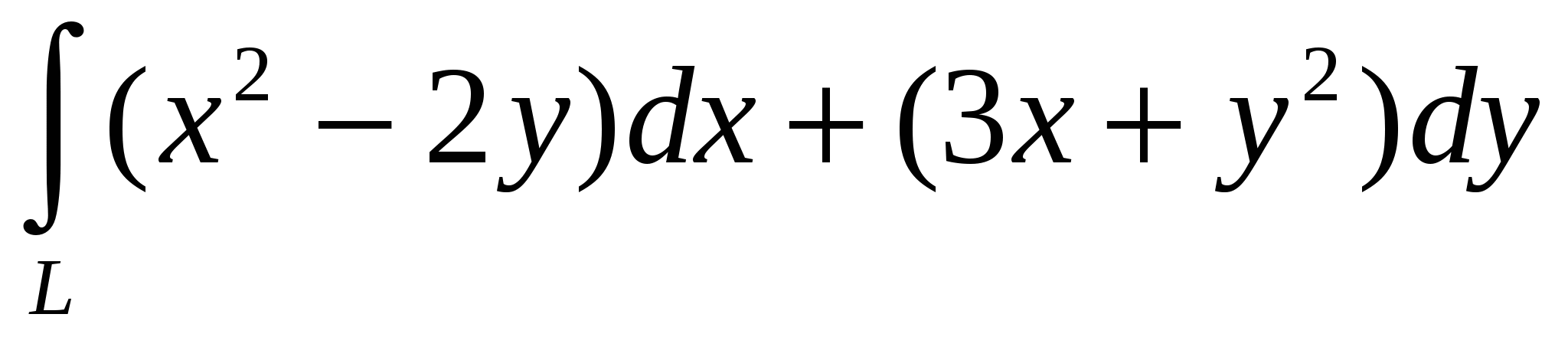 , где L- контур треугольника, образованного осями координат и прямой , где L- контур треугольника, образованного осями координат и прямой 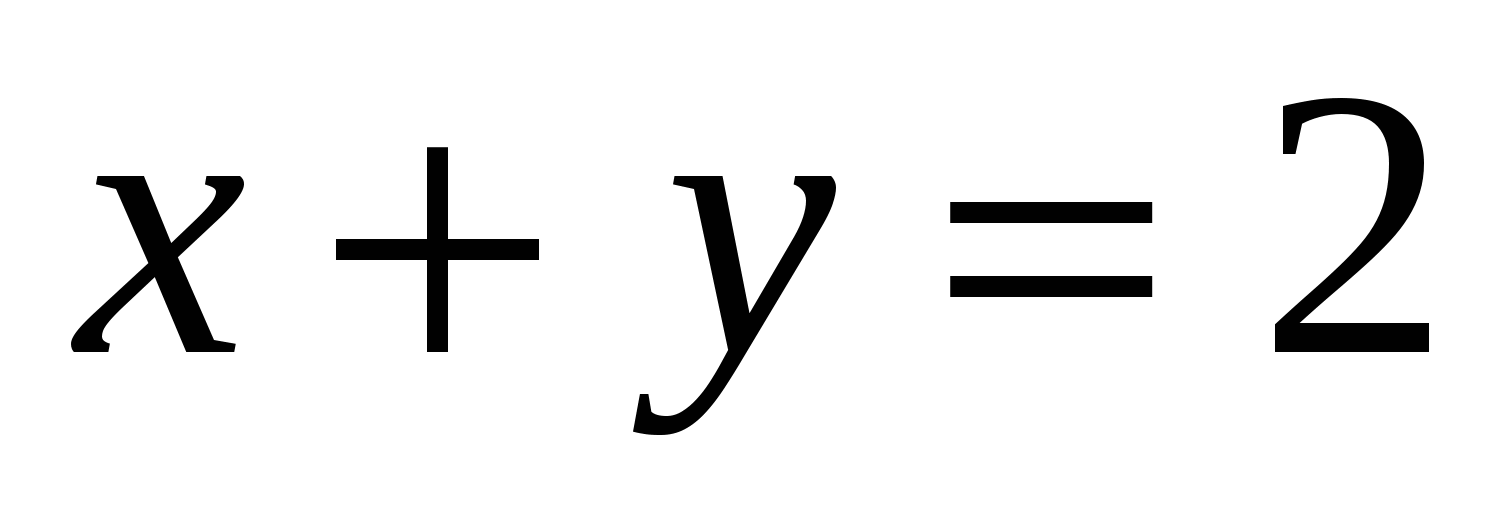 . .
|
1. 10;
2. 1;
3. 0;
4. -1.
|
19
|
Если кривая АВ задается уравнением 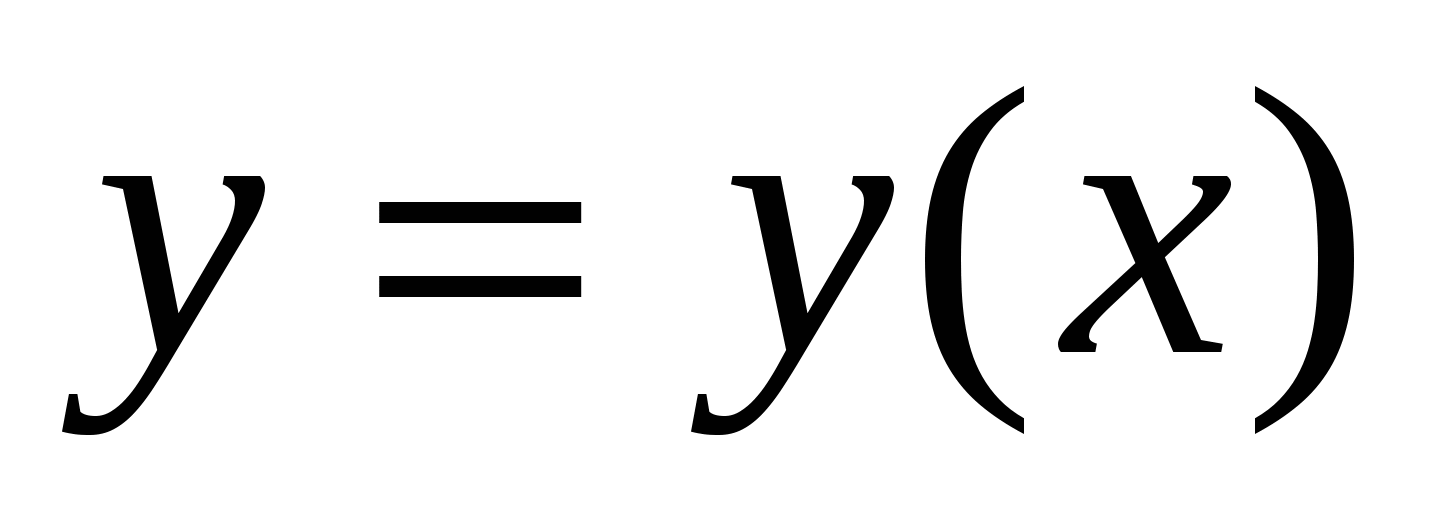 , точка А имеет координаты (a;y(a)), точка В- координаты (b;y(b)), то криволинейный интеграл второго рода , точка А имеет координаты (a;y(a)), точка В- координаты (b;y(b)), то криволинейный интеграл второго рода 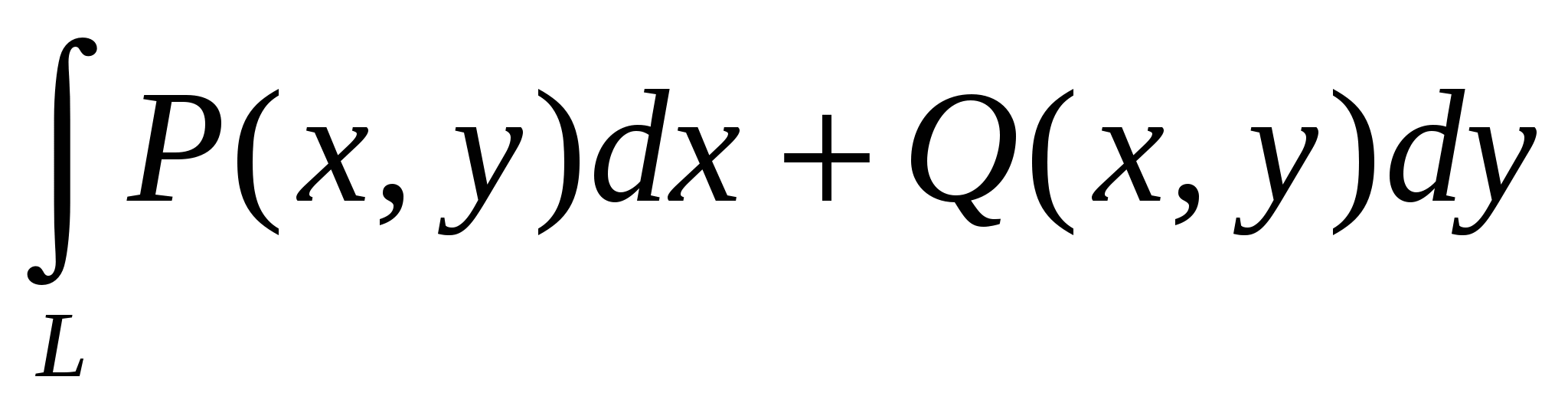 = =
|
1. 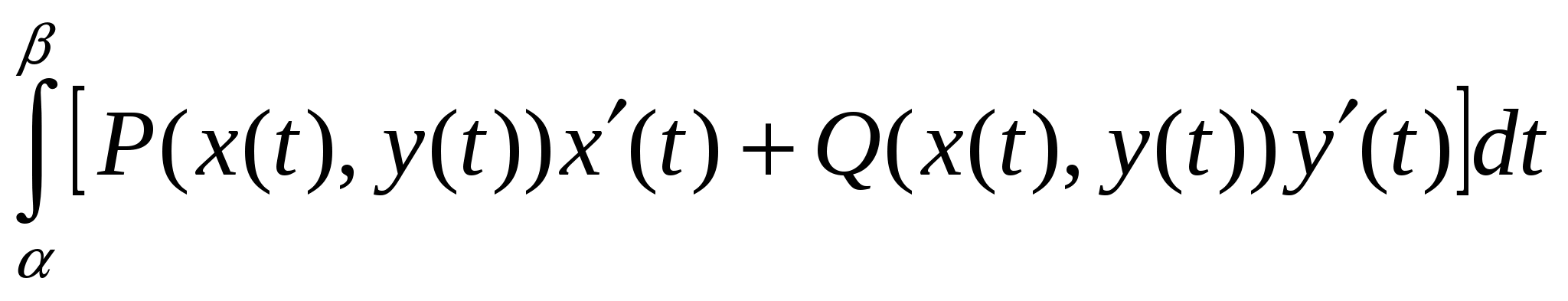 ; ;
2. 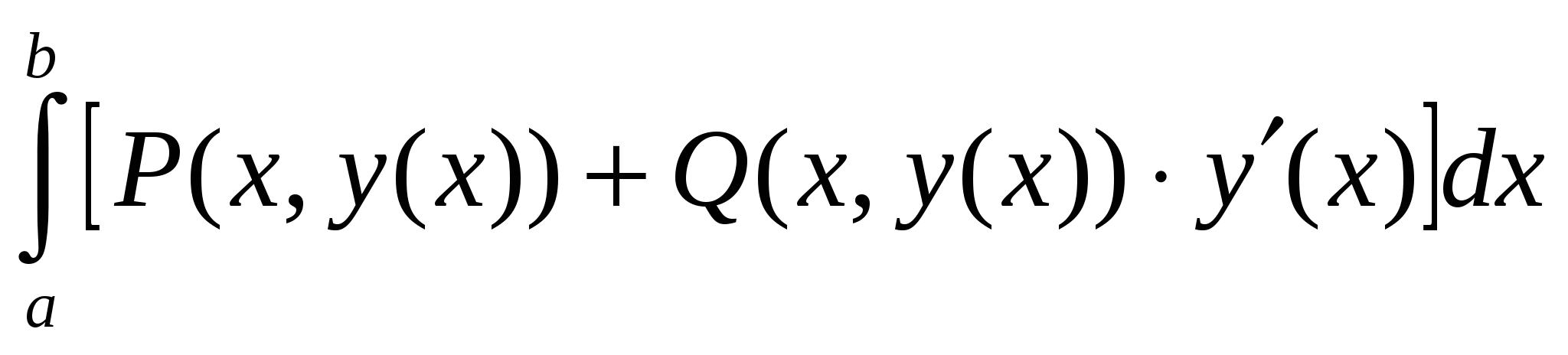 ; ;
3. 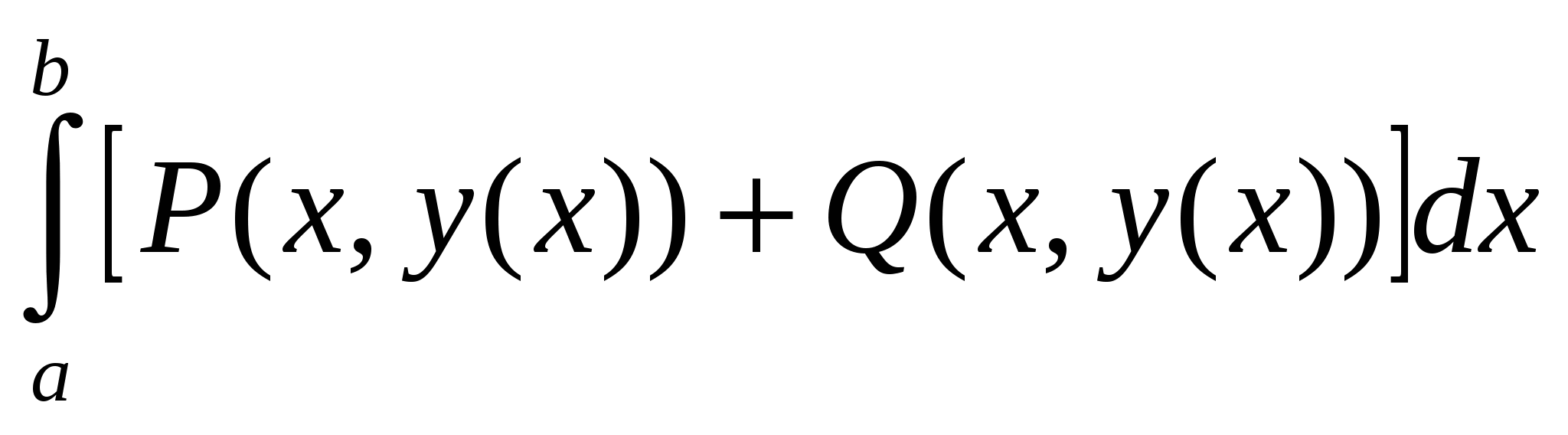 ; ;
4. 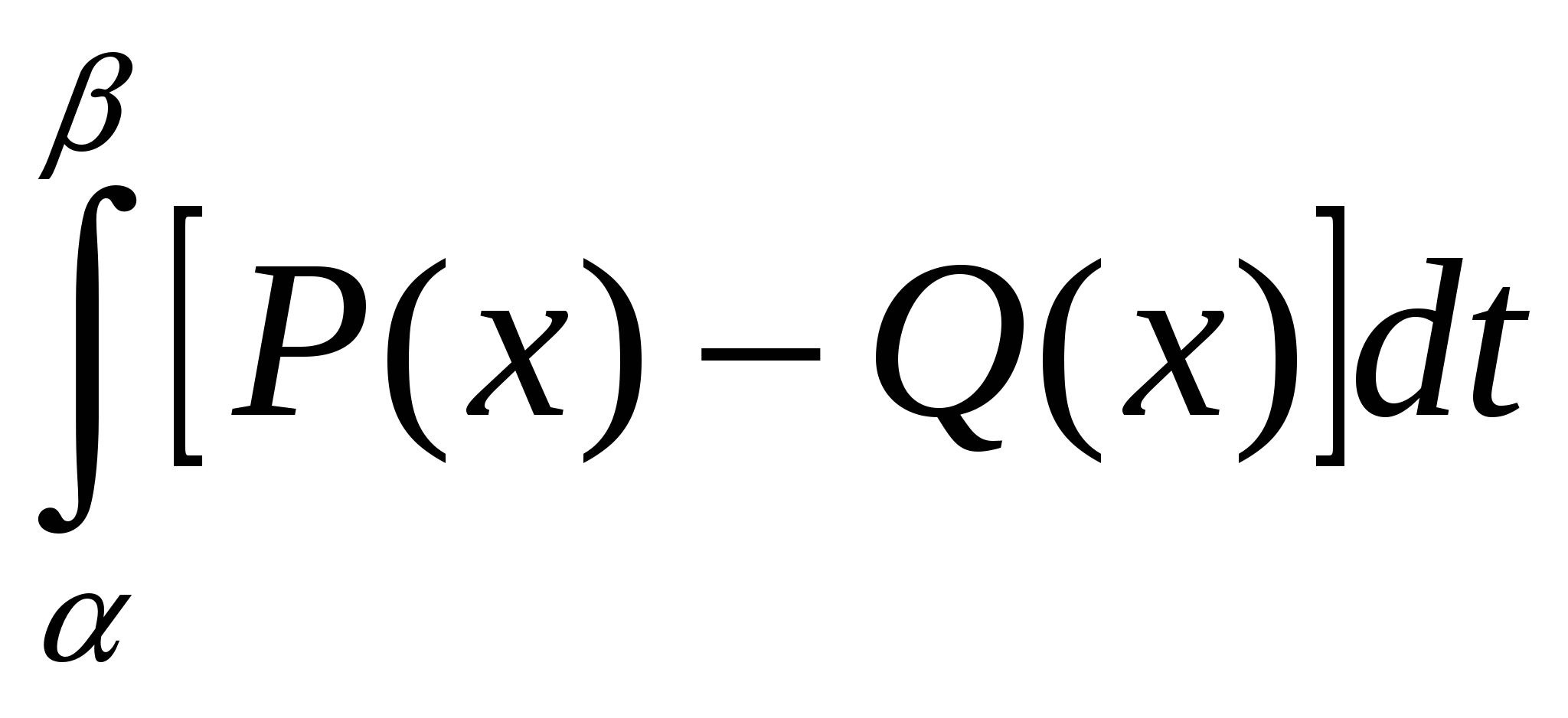 . .
|
20
|
Найти криволинейный интеграл 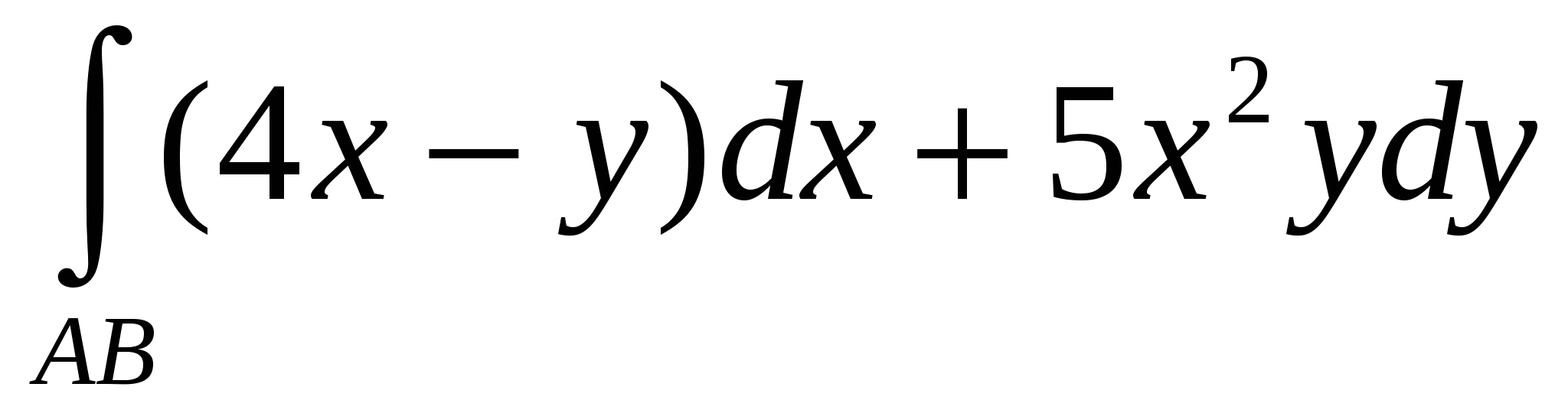 , если АВ есть дуга параболы , если АВ есть дуга параболы 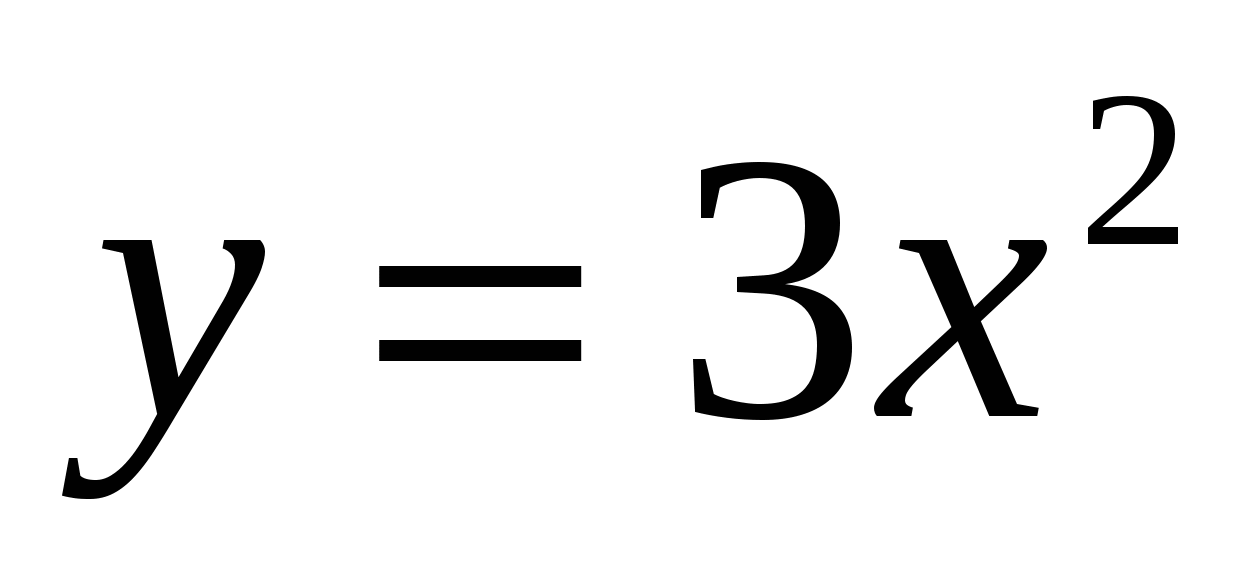 , А=(0,0), В=(1,3). , А=(0,0), В=(1,3).
|
1. 5;
2. 4;
3. 16;
4. 3.
|
21
|
Продолжите определение: «Кривая называется гладкой, если в в каждой ее точке существует………»
|
1. касательная, непрерывно изменяющаяся вдоль кривой.
2. разрыв 1 рода.
3. разрыв 2 рода.
4. бесчисленное множество касательных.
|
22
|
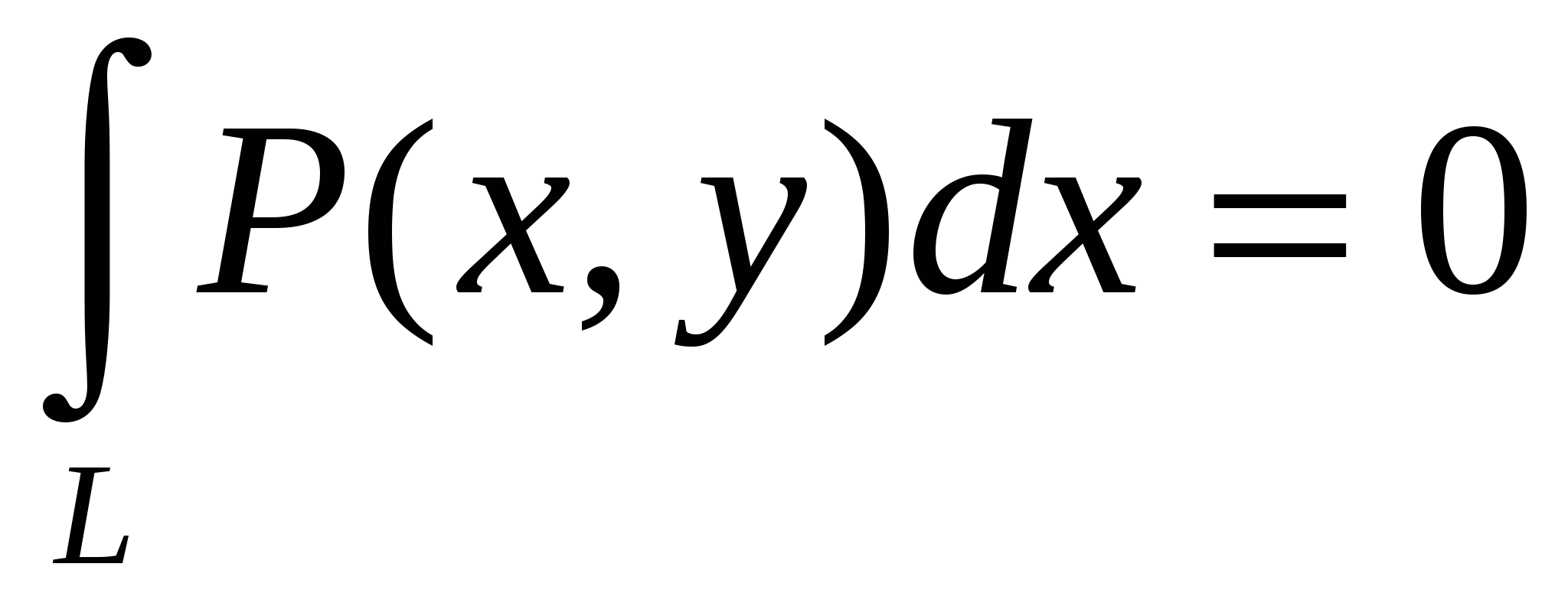 , , 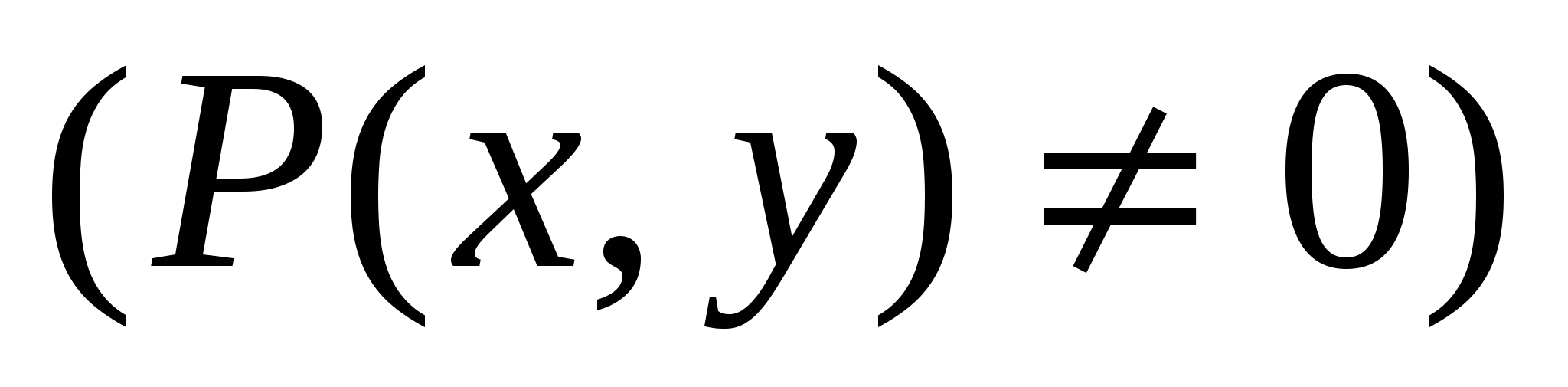 если…. если….
|
1. 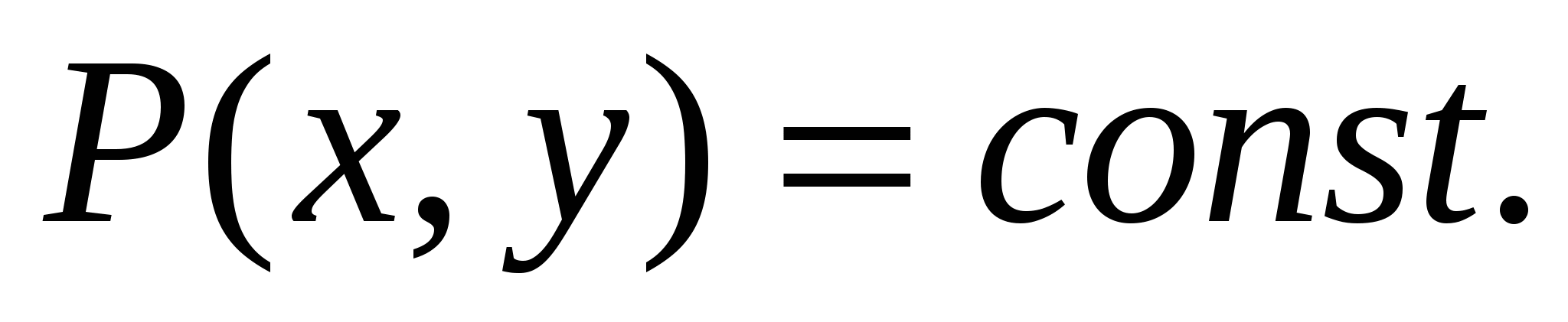
2. кривая L лежит в плоскости перпендикулярной оси Ox.
3. кривая L лежит в плоскости перпендикулярной оси Oy.
4. кривая L лежит в плоскости xOy.
|
23
|
Интеграл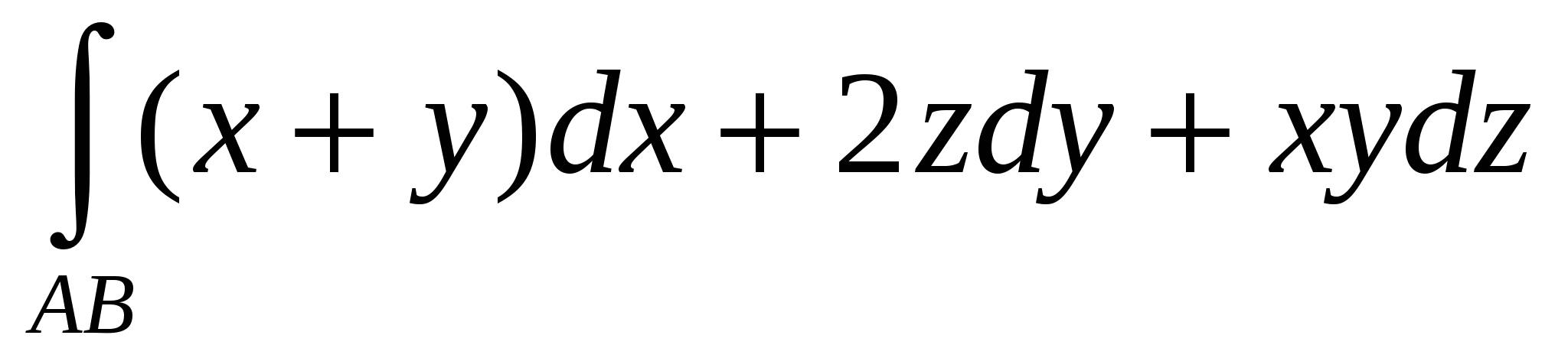 , если АВ ─ дуга линии: , если АВ ─ дуга линии: 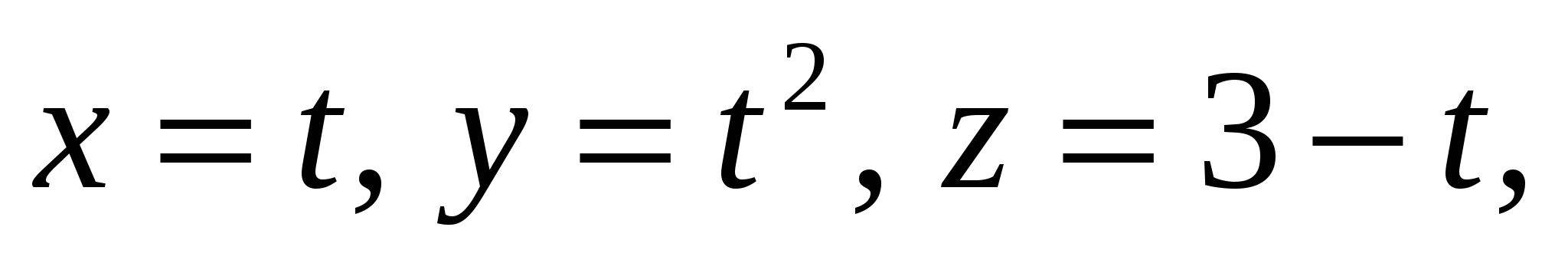 причем tA=1, tB=2 можно привести к виду: причем tA=1, tB=2 можно привести к виду:
|
1. 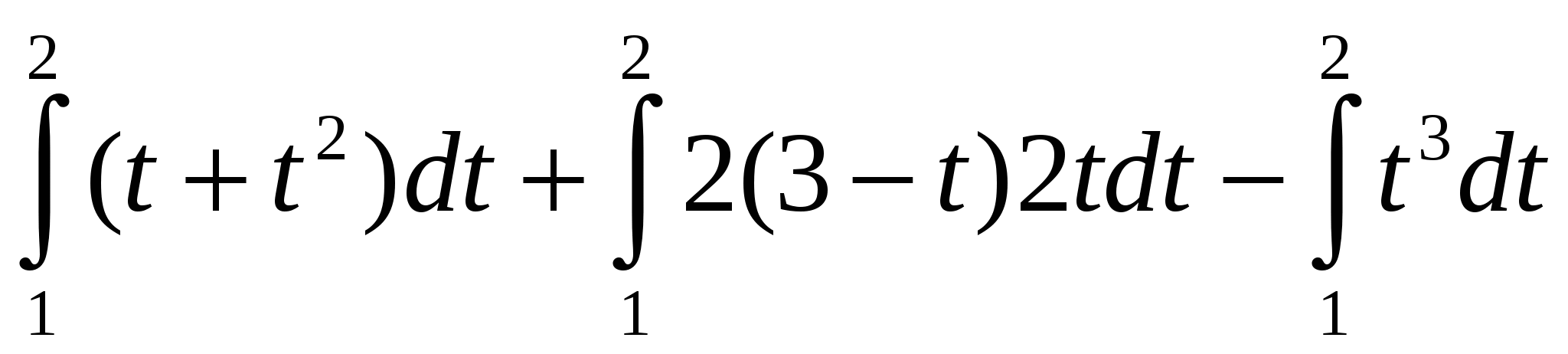 ; ;
2. 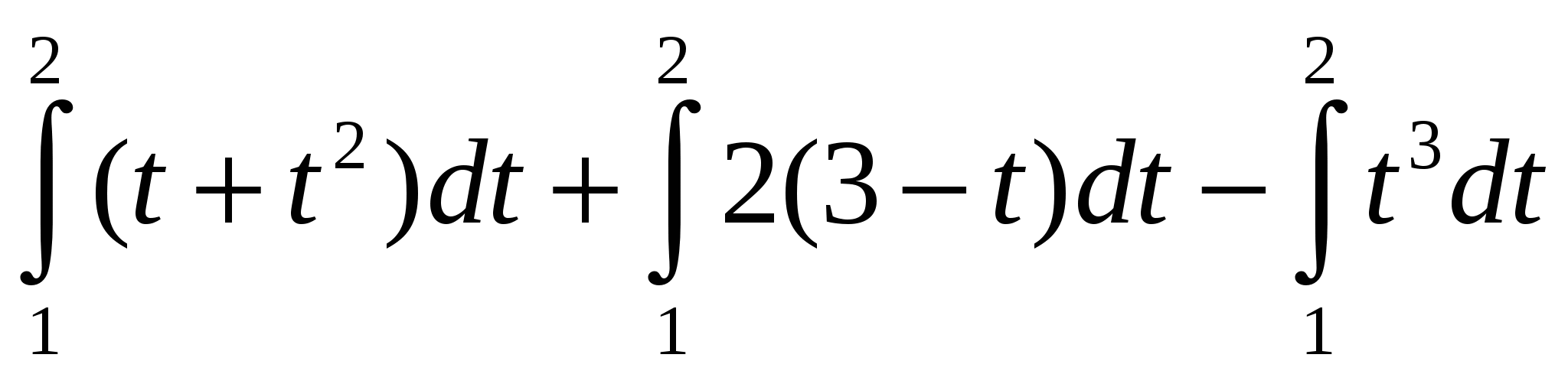 ; ;
3. 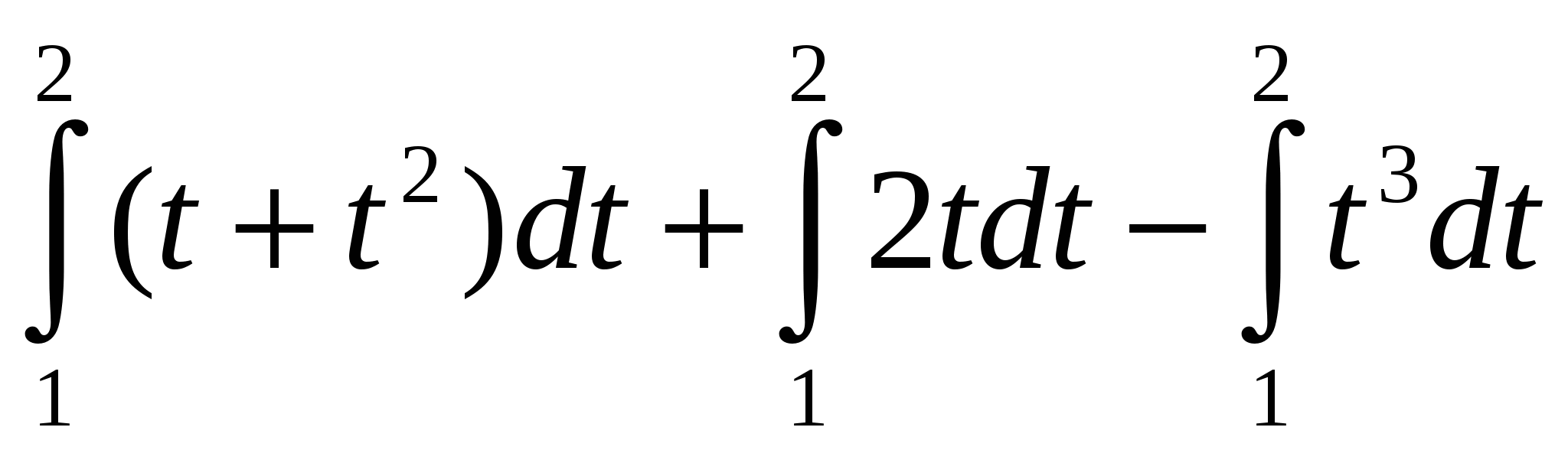 ; ;
4. 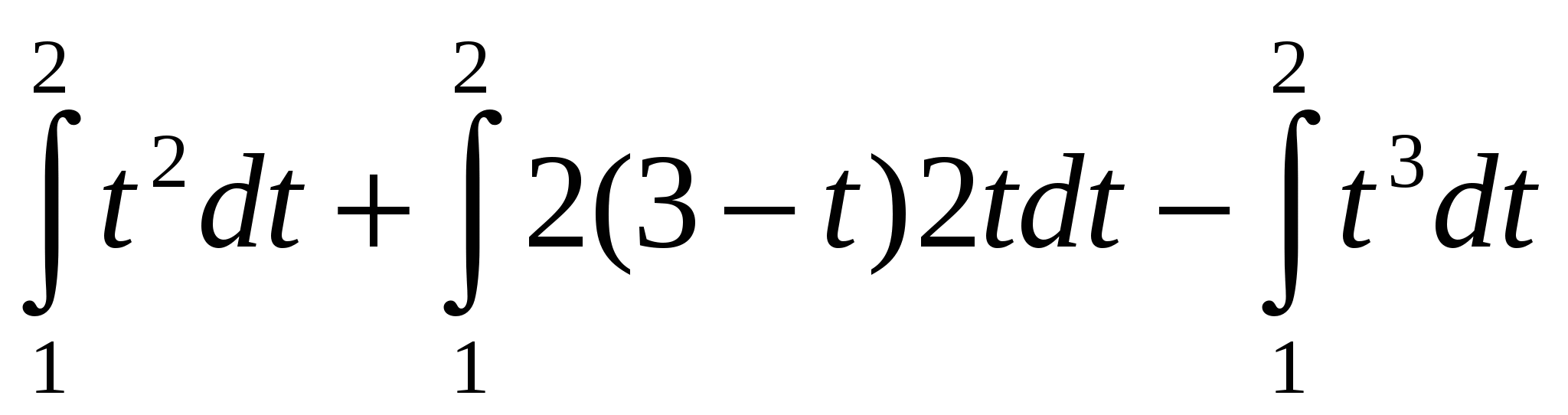 . .
|
24
|
Продолжите свойство криволинейного интеграла 2 рода: «Криволинейный интеграл по замкнутой кривой не зависит…….»
|
1. от знака интеграла.
2. от коэффициента, стоящего перед интегралом.
3. от выбора начальной точки, но зависит от направления обхода кривой.
4. от направления обхода кривой.
|
25
|
Вычислите по формуле Грина интеграл 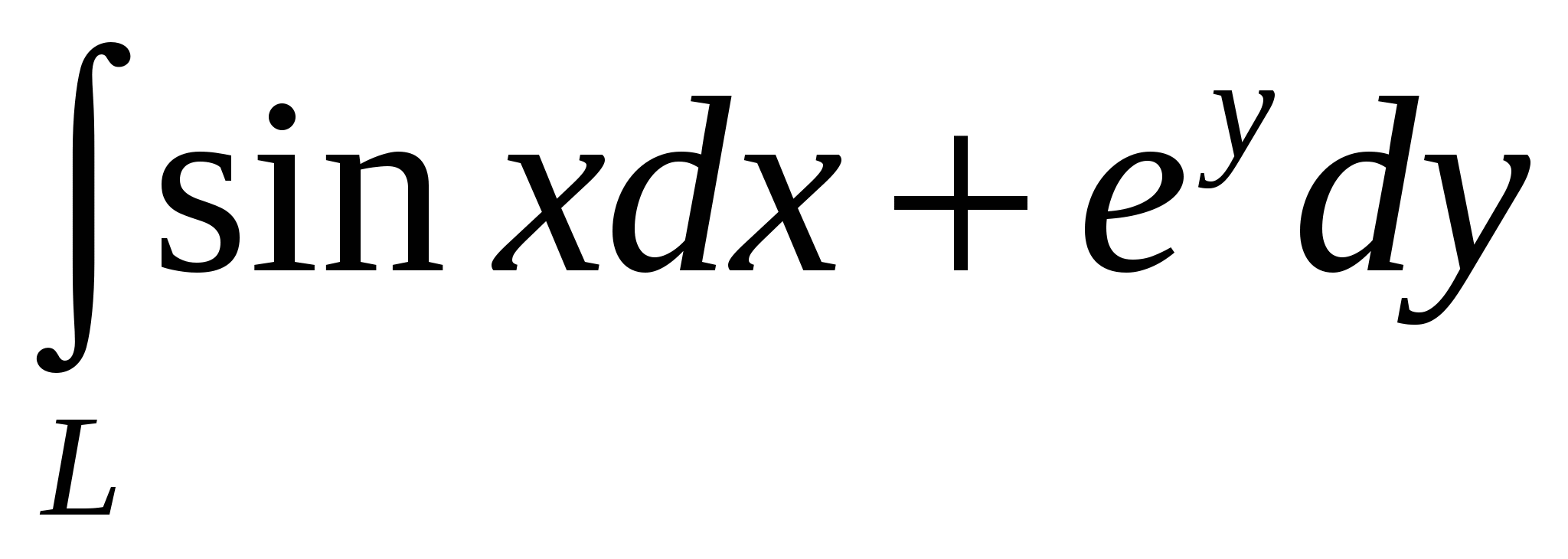 , если кривая , если кривая  представляет собой окружность, описанную уравнением представляет собой окружность, описанную уравнением 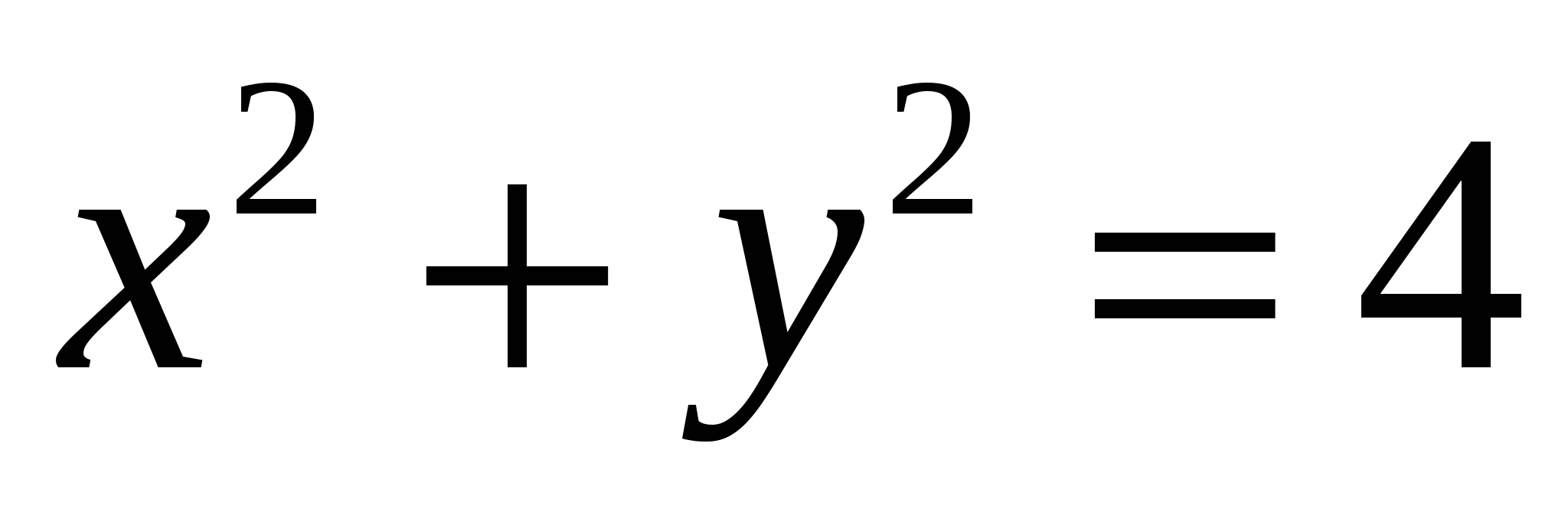 . .
|
1. 2;
2. 3;
3. 4;
4. 0.
|
 Скачать 234 Kb.
Скачать 234 Kb.