№
|
Вопросы
|
Варианты ответов
|
|
ЧИСЛОВЫЕ РЯДЫ
|
|
|
КАТЕГОРИЯ 1
|
|
|
Ряд сходится, если
(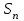 — его — его 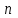 -я частичная сумма) -я частичная сумма)
|
1.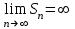
2.
3.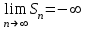
4.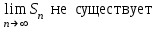
|
|
Что называется остатком числового ряда 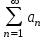 ? ?
|
1. 
2. 
3. 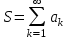
4. 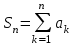
|
|
Что такое 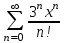 -я частичная -я частичная
сумма ряда 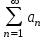 ? ?
|
1.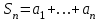
2.
3.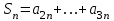
4.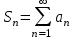
|
|
Указать общий член
ряда
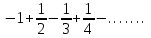
|
1.
2. 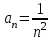
3. 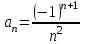
4. 
|
|
Указать необходимый признак сходимости.
|
Если 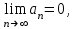 то ряд сходится. то ряд сходится.
Если 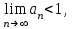 то ряд сходится. то ряд сходится.
Если 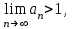 то ряд сходится. то ряд сходится.
Если ряд сходится, то 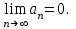
|
|
Если ряд 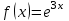 сходится, то ряд сходится, то ряд 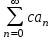 , где , где 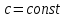 , ,
|
сходится только при 
расходится
расходится при 
сходится
|
|
Какой из указанных числовых рядов сходится?
|
1.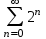
2.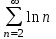
3.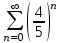
4.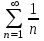
|
|
Указать гармонический ряд
|
1.
2.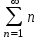
3.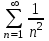
4.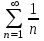
|
|
В чем заключается достаточный признак расходимости?
|
1.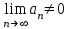
2.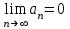
3.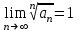
4.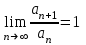
|
|
Указать, когда ряд Дирихле 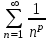 сходится сходится
|
1.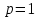
2.
3.
4.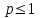
|
|
Числовые ряды 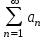 и и 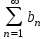 одновременно сходятся или расходятся, если одновременно сходятся или расходятся, если
|
1.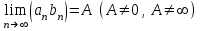
2.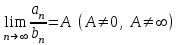
3.
4.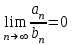
|
|
Какой числовой ряд проще исследовать по теореме сравнения в предельной форме (сравнить с рядом 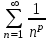 ) ? ) ?
|
1. 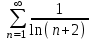
2. 
3. 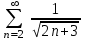
4.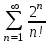
|
|
С каким рядом надо сравнивать ряд 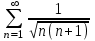 , чтобы установить его сходимость (расходимость)? , чтобы установить его сходимость (расходимость)?
|
1.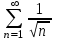
2.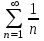
3.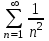
4.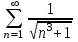
|
|
Если для ряда 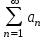
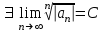 , то , то
|
при 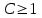 ряд сходится ряд сходится
при 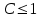 ряд расходится ряд расходится
при 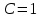 ряд сходится ряд сходится
при 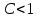 ряд абсолютно сходится ряд абсолютно сходится
|
|
Каким признаком лучше всего исследовать ряд 
|
Признаком Коши
Признаком Даламбера
Интегральным признаком Коши
Признаком сравнения
|
|
C помощью какого из признаков можно исследовать данный ряд 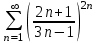
на сходимость
|
1.интегральный признак Коши
2.радикальный признак Коши
3.признак сравнения
4.признак сравнения в предельной форме
|
|
Чему равен предел при исследовании ряда 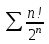
по признаку Даламбера?
|
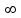
1
0
2
|
|
Чему равен предел при исследовании ряда 
по признаку Коши (радикальному)?
|
1. 0
2. 1
3. 3
4. 1/3
|
|
Какие условия являются достаточными для сходимости знакочередующегося ряда
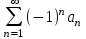
(признак Лейбница)?
|
 , , 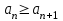
 , , 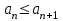
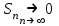 , , 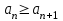
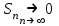 , , 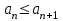
|
|
Знакопеременный ряд 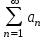 (ряд А) называется абсолютно сходящимся (ряд А) называется абсолютно сходящимся
|
1.Если ряд 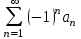 сходится сходится
2.Если ряд А сходится, а ряд  расходится расходится
3.Если ряд А сходится, то 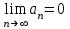
4.Если ряд  сходится сходится
|
|
Почему ряд 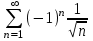
является условно сходящимся?
|
1.Т.к. расходится ряд 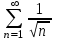
2.Т.к. сходится ряд 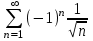 , а ряд , а ряд 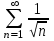 расходится расходится
3.Т.к. сходится ряд 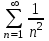
4.Т.к. 
|
|
Почему ряд 
является абсолютно сходящимся?
|
1.Т.к. 
2.Т.к. сходится ряд 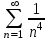
3.Т.к. 
4.Т.к. 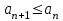
|
|
Указать правильное окончание теоремы Лейбница:
Ряд 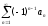 сходится, если сходится, если
|
выполнены два условия а)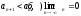
выполнены два условия
выполнены два условия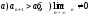

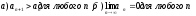
|
|
Какой числовой ряд можно исследовать по признаку Лейбница
|
1.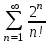
2. 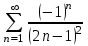
3. 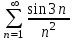
4. 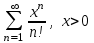
|
|
Ряд 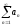 (ряд А) называется условно сходящимся (ряд А) называется условно сходящимся
|
1.Если ряд 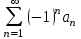 сходится сходится
2.Если ряд А сходится, а ряд  расходится расходится
3.Если ряд А сходится, то 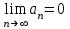
4.Если ряд  сходится сходится
|
|
КАТЕГОРИЯ 2
|
|
|
Ряд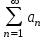 сходится тогда и только тогда, когда сходится тогда и только тогда, когда
|
1. Последовательность его частичных сумм ограничена
2. 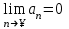
3. Последовательность его частичных сумм сходится
4. Последовательность его частичных сумм сходится к нулю
|
|
Для какого из данных рядов выполняется необходимый признак сходимости?
|
1.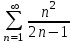
2.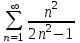
3.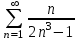
4. 
|
|
Положительный ряд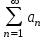 сходится тогда и только тогда, когда сходится тогда и только тогда, когда
|
1.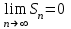 ( (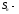 частичная сумма ряда) частичная сумма ряда)
2. 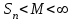
3.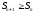
4. 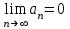 5. 5.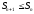
|
|
Указать общий член
ряда
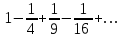
|
1.
2. 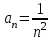
3. 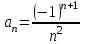
4. 
|
|
Если ряды 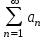 и и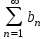 сходятся, то, сходятся ли ряды сходятся, то, сходятся ли ряды 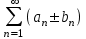 ? ?
|
1.сходятся
2.невозможно определить
3. ряд 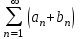 расходится, а ряд расходится, а ряд 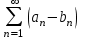 сходится сходится
4.расходятся
|
|
Указать геометрический ряд
|
1.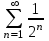
2..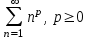
3.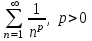
4. 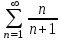
|
|
Какой из указанных числовых рядов сходится?
|
1.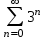
2.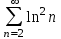
3. 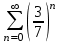
4. 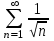
|
|
Указать ряд Дирихле
|
1.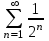
2.
3.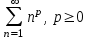
4.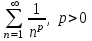
|
|
Сформулируйте достаточный признак расходимости?
|
1.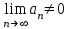
2.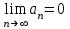
3.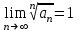
4.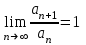
|
|
Какое из приведенных утверждений верно?
|
Если 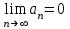 , то ряд , то ряд 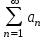 сходится сходится
Если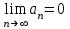 , то ряд , то ряд 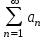 расходится расходится
Если ряд 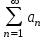 расходится, то расходится, то 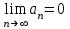
Если ряд 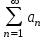 сходится, то сходится, то 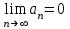
|
|
Члены рядов А: 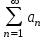 и В: и В: 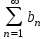 удовлетворяют условию: удовлетворяют условию: 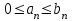 , тогда , тогда
|
если сходится А, то сходится В
если сходится В, то сходится А
А сходится, В расходится
А и В сходятся или расходятся одновременно
|
|
Для положительных рядов
А: 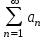 и В: и В: 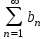
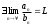 , тогда , тогда
|
ряды А и В сходятся одновременно, только если 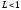
ряды А и В расходятся одновременно, только если 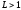
если  , А сходится, а В расходится , А сходится, а В расходится
ряды А и В сходятся или расходятся одновременно, если 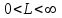
|
|
Какой числовой ряд проще исследовать по теореме сравнения в предельной форме (сравнить с рядом 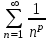 ) ? ) ?
|
1. 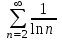
2. 
3. 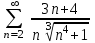
4.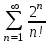
|
|
Если для ряда 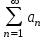
 , то , то
|
при 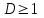 ряд сходится ряд сходится
при 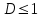 ряд расходится ряд расходится
при 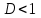 ряд абсолютно сходится ряд абсолютно сходится
при 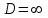 ряд сходится ряд сходится
|
|
Какой ряд можно исследовать по признаку Даламбера?
|
1. 2. 2.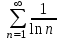 3. 3.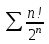
4.
|
|
Каким признаком лучше всего исследовать ряд 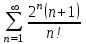
|
Признаком Коши
Признаком Даламбера
Интегральным признаком Коши
Признаком сравнения
|
|
C помощью какого из признаков можно исследовать данный ряд 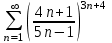
на сходимость
|
1.интегральный признак Коши
2.радикальный признак Коши
3.признак сравнения
4.признак сравнения в предельной форме
|
|
Какой ряд целесообразно исследовать по радикальному признаку Коши?
|
1. 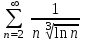
2. 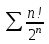
3.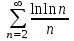
4.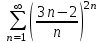
|
|
Какой ряд целесообразно исследовать по интегральному признаку Коши?
|
1.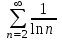
2. 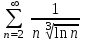
3. 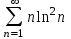
4.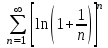
|
|
C помощью какого из признаков можно исследовать данный ряд
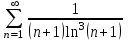
на сходимость
|
1.интегральный признак Коши
2.радикальный признак Коши
3.признак сравнения
4.признак сравнения в предельной форме
|
|
С помощью интегрального признака Коши установить, какие из приведенных ниже рядов сходятся
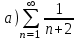 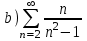
 
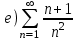
|

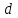
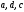
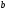
|
|
Сформулируйте признак Лейбница:
Знакочередующийся ряд 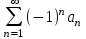 сходится, если сходится, если
|
 , , 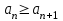
 , , 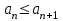
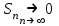 , , 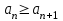
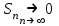 , , 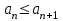
|
|
Указать достаточный признак сходимости знакопеременного числового ряда 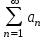 (ряда А) (ряда А)
|
1.Если ряд 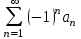 сходится, то сходится ряд А сходится, то сходится ряд А
2.Ряд А сходится, а ряд  расходится расходится
3.Если ряд А сходится, то 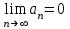
4.Если ряд  сходится, то ряд А сходится абсолютно сходится, то ряд А сходится абсолютно
|
|
Установить, какие из приведенных ниже рядов сходятся абсолютно
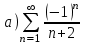 
 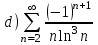

|
1. 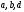
2. 
3. 
4. 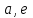
|
|
Почему ряд 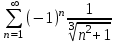
является условно сходящимся?
|
1.Т.к. расходится ряд 
2.Т.к. сходится ряд 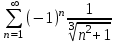 , а ряд , а ряд  расходится расходится
3.Т.к. сходится ряд 
4.Т.к. 
|
 Скачать 406.63 Kb.
Скачать 406.63 Kb.