Новый документ (12). Исходное выражение можно упростить Тогда исходный ряд можно представить в виде
 Скачать 216.38 Kb. Скачать 216.38 Kb.
|
 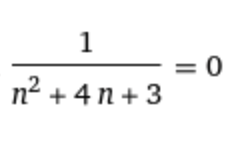  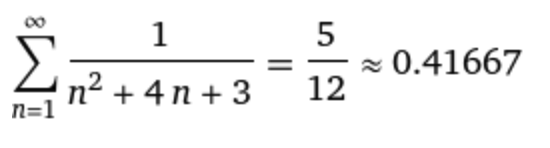 а) Исходное выражение можно упростить: Тогда исходный ряд можно представить в виде: Применим сравнительный признак: α=2 Поскольку α больше 1, то ряд сходится. б) Исходное выражение можно упростить: Тогда исходный ряд можно представить в виде: Применим радикальный признак Коши: Поскольку: Получаем: Поскольку полученное значение равно 1, то получаем неопределенность. Признак Даламбера. при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность (дополнительные исследования). Поскольку q = 1, то получаем неопределенность. в) Признак Даламбера. при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность (дополнительные исследования).  = = Поскольку q < 1, то ряд сходится. Рассмотрим первые три члена ряда: Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница. а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется б) По второму признаку Лейбница предел ряда должен стремится к 0 Второе условие Лейбница выполняется. Таким образом, рассматриваемый ряд сходится. Чтобы говорить об абсолютной или условной сходимости, необходимо исследовать ряд по одному из признаков сходимости рядов. Исходное выражение можно упростить: Тогда исходный ряд можно представить в виде:  Применим сравнительный признак: α=1/2 Поскольку α меньше 1, то ряд расходится. Следовательно, ряд сходится условно. Дан ряд  Это ряд вида 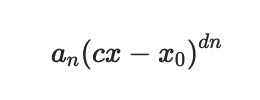 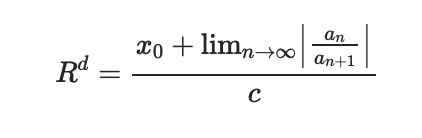    Тогда  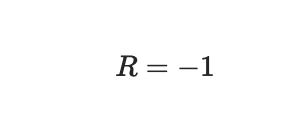 5.  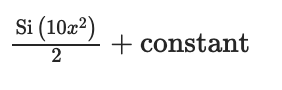 |
