ргр по рядам. Решение Выполним промежуточную проверку
 Скачать 19.87 Kb. Скачать 19.87 Kb.
|
|
Задание 1: Найти сумму ряда 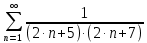 Решение: 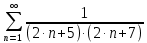 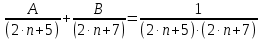 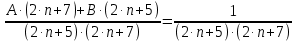 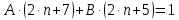 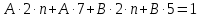 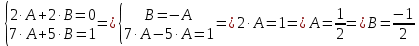 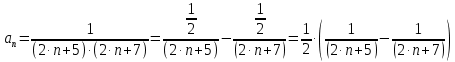 Выполним промежуточную проверку: 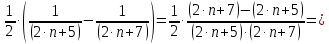 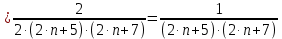 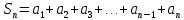 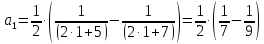 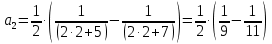 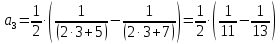 … 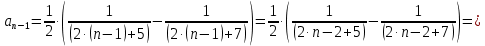 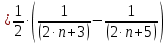 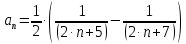 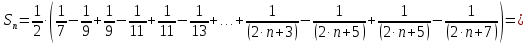 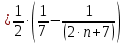 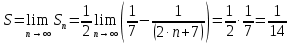 Задание 2: Исследовать ряд на сходимость (или расходимость) 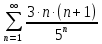 Решение: 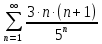 Применим радикальный признак Коши 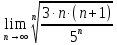 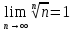 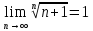 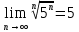 Получаем: 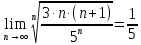 Поскольку полученное значение меньше единицы, то ряд сходится Задание 3: Исследовать ряд на сходимость (или расходимость) 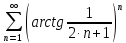 Решение: 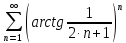 Исходное выражение можно упростить: 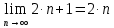 Тогда исходный ряд можно представить в виде: 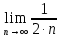 Исследуем сходимость ряда при помощи интегрального признака Коши. Рассмотрим несобственный интеграл 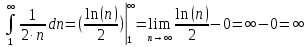 Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Задание 4: Исследовать ряд на сходимость (или расходимость) 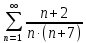 Решение: 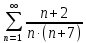 Исходное выражение можно упростить: 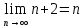 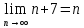 Тогда исходный ряд можно представить в виде: 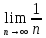 Исследуем сходимость ряда при помощи интегрального признака Коши. Рассмотрим несобственный интеграл 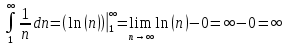 Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Задание 5: Исследовать ряд на сходимость (условную или абсолютную) или расходимость 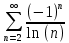 Решение: 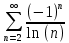 Рассмотрим первые три члена ряда: 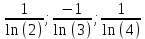 Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница. 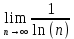 а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется 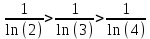 б) По второму признаку Лейбница предел ряда должен стремится к 0. 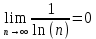 Второе условие Лейбница выполняется. Таким образом, рассматриваемый ряд сходится. Чтобы говорить об абсолютной или условной сходимости, необходимо исследовать ряд по одному из признаков сходимости рядов. Исходное выражение можно упростить: 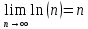 Тогда исходный ряд можно представить в виде 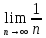 Исследуем сходимость ряда при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл: 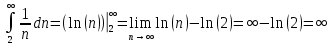 Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Следовательно, ряд сходится условно. Задание 6: найти область сходимости ряда 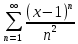 Решение: Общий член ряда имеет вид: 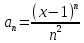 Таким образом: 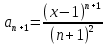 Значит: 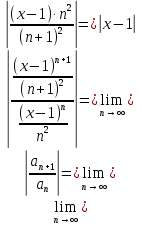 Следовательно, ряд сходится, если: 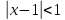 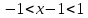 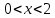 При 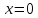 ряд принимает вид: ряд принимает вид: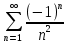 - знакочередующийся ряд с монотонно убывающими по абсолютной величине, стремящимися к нулю членами. Такой ряд сходится (по теореме Лейбница). При 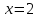 ряд принимает вид: ряд принимает вид: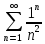 - такой ряд также сходится (обобщенный гармонический ряд). Окончательно получаем область сходимости исходного ряда: [0;2] Задание 7: вычислить интеграл с точность 0,001 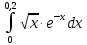 Решение 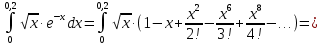 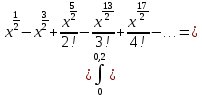 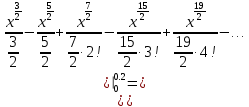 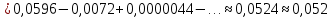 Задание 8: Разложить функцию в ряд по степеням (а-х) 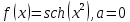 Решение: Разложение задается следующей формулой: 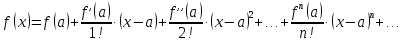 При а=0 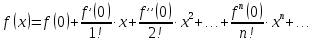 Получаем: 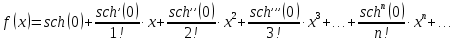 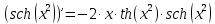 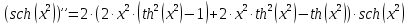 При а=0 получим 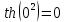 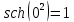 Тогда получим: 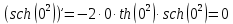 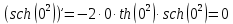 Следовательно: 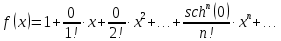 Задание9: решить приближенно с помощью рядов ДУ:  Решение: 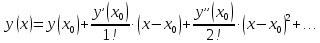 В нашем случае: 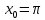 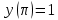 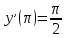 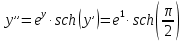 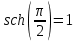 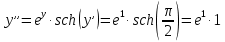 Тогда получим: 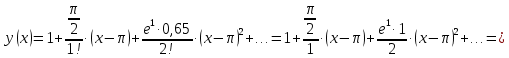 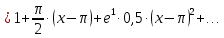 Ответ: 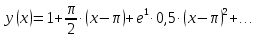 |
