Контрольная работа по высшей математике №9. Решение Разложим общий член ряда на сумму простейших дробей методом неопределенных коэффициентов Откуда
 Скачать 270.33 Kb. Скачать 270.33 Kb.
|
|
Контрольная работа № 9 Задание 1. Пользуясь определением сходимости числового ряда, исследовать на сходимость заданный ряд и в случае сходимости найти его сумму. 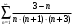 Решение: Разложим общий член ряда на сумму простейших дробей методом неопределенных коэффициентов: 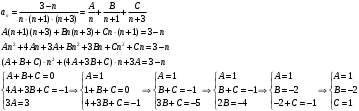 Откуда: 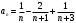 Находим n-ю частичную сумму: 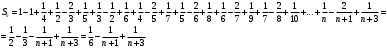 Следовательно, согласно определениям сходимости ряда и его суммы, получаем: 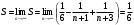 Т.е. данный ряд сходится и его сумма равна: 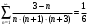 Задание 2. Исследовать на сходимость знакопостоянные ряды 1. 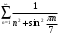 Воспользуемся сходящимся рядом Дирихле 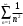 . Так как: . Так как: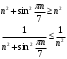 Т.к. члены исследуемого ряда не превосходят соответствующих членов сходящегося ряда, то согласно первому признаку сравнения, исследуемый ряд также сходится. 2. 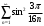 Воспользуемся сходящимся рядом Дирихле 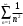 . Так как: . Так как: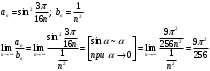 Т.к. указанный предел имеет конечное значение, то согласно второму признаку сравнения оба ведут себя одинаково. Т.е. исследуемый ряд также сходится. 3. 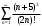 Воспользуемся признаком Даламбера: 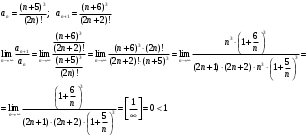 Т.к. указанный предел меньше 1, то, согласно признаку Даламбера, ряд сходится. 4. 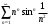 Воспользуемся радикальным признаком Коши: 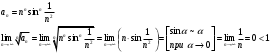 Т.к. указанный предел меньше 1, то, согласно радикальному признаку Коши, ряд сходится. 5. 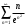 Воспользуемся интегральным признаком Коши. Исследуем сходимость несобственного интеграла: 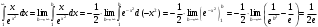 Т.е. несобственный интеграл сходится. Согласно интегральному признаку Коши сходится и исследуемый ряд. Задание 3.2. Исследовать на сходимость знакопеременный ряд: 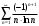 Решение: Воспользуемся признаком Лейбница. Проверим выполнимость первого критерия. Очевидно, что с увеличением n знаменатель дроби увеличивается, следовательно, сама дробь уменьшается. Т.е. первый критерий выполняется: 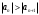 Проверим выполнимость второго критерия 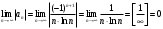 Оба критерия признака Лейбница выполняются. Следовательно, исследуемый ряд сходится. Задание 4. Найти области сходимости степенных рядов: 1. 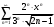 Находим радиус сходимости ряда: 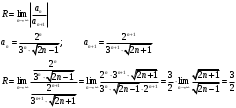 Т.о. интервал сходимости ряда имеет вид: 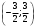 Исследуем сходимость ряда на концах интервала: 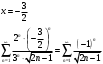 Получили числовой знакочередующийся ряд, который сходится согласно признаку Лейбница: 1) очевидно, что с увеличением n модули членов ряда монотонно убывают: 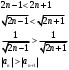 2) 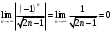 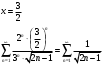 Получили числовой знакоположительный ряд, который сравним с рядом Дирихле: 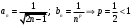 Т.о. ряд расходится Окончательно область сходимости ряда имеет вид: 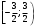 2. 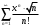 Находим радиус сходимости ряда: 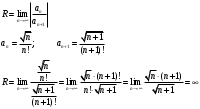 Т.о. интервал сходимости ряда имеет вид: 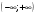 Задание 5. Разложить в степенной ряд по степеням х заданные функции 1. 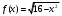 Воспользуемся разложением в ряд функции 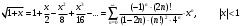 Преобразуем исходную функцию: 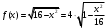 Подставим вместо х выражение 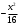 : :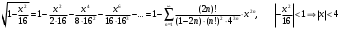 Тогда: 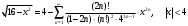 2. 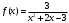 Данная функция представляет собой рациональную дробь. Разложим ее на сумму простейших дробей методом неопределенных коэффициентов: 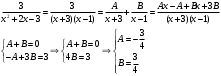 Откуда: 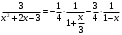 Воспользуемся рядом: 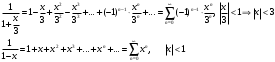 Откуда: 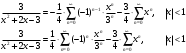 Задание 8. Пользуясь табличными (известными) разложениями элементарных функций в степенные ряды (ряды Тейлора и Маклорена), вычислить (методом выделения главной части) предел заданной функции. 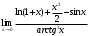 Решение: Воспользуемся табличными разложениями: 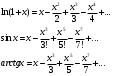 Откуда: 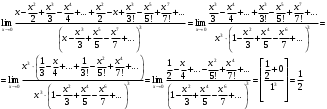 Задание 10. Найти решение данного дифференциального уравнения в виде степенного ряда, удовлетворяющее заданным начальным условиям: 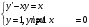 Решение: Ищем решение данной задачи Коши в окрестности точки х = 0 в виде степенного ряда 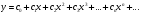 , где , где 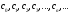 – коэффициенты, подлежащие определению – коэффициенты, подлежащие определениюПродифференцируем ряд: 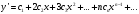 Используя начальные условия 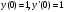 , находим: , находим: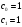 Подставим в исходное уравнение значения х, у и у' с учетом найденных коэффициентов, получим: 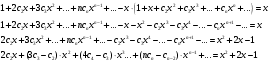 Приравниваем коэффициенты при одинаковых степенях х левой и правой частей, будем иметь бесконечную систему уравнений: 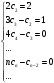 Откуда: 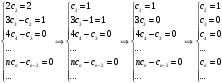 Откуда решение уравнения имеет вид: 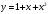 Задание 11. Разложить заданную функцию в тригонометрический ряд Фурье и определить для периодического продолжения функции на 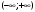 частотный, амплитудно-частотный и фазово-частотный спектры. частотный, амплитудно-частотный и фазово-частотный спектры.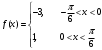 Решение: Запишем тригонометрический ряд Фурье, соответствующий данной функции 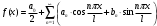 и найдем входящие сюда коэффициенты 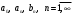 по формулам Эйлера-Фурье по формулам Эйлера-Фурье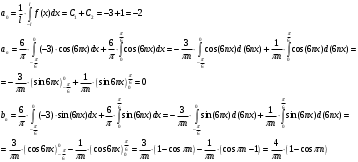 Т.о. 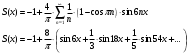 причем 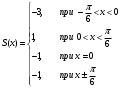 Частотный, амплитудно-частотный и фазово-частотный спектры представляют собой соответственно: 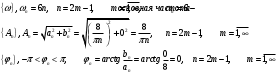 Контрольная работа № 10 1. Найти все значения корня из комплексного числа. 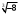 Решение: Представим комплексное число z = -8 в тригонометрической форме: 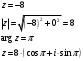 По формуле Муавра находим корни: 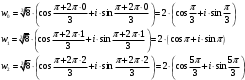 2. Начертить область, заданную неравенствами. 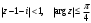 Решение: Пусть z = x+ yi. Тогда: 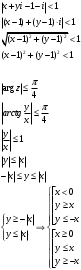 Строим область, определяемую полученными неравенствами: 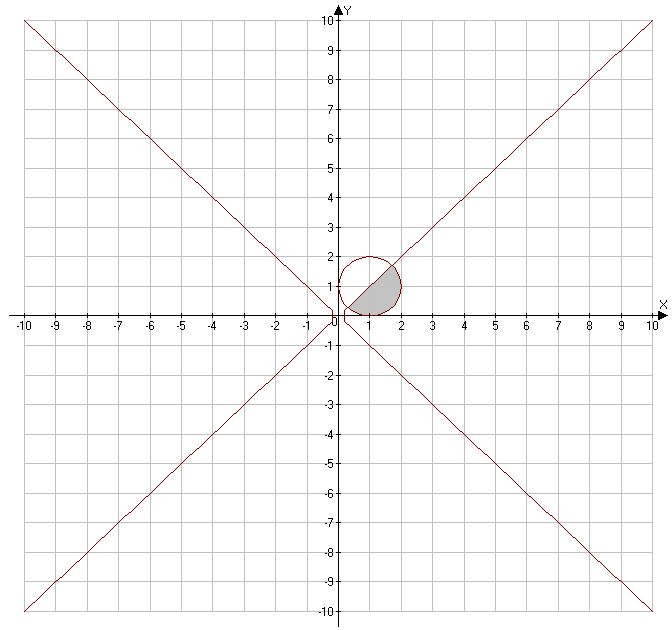 3. Пользуясь условиями Коши-Римана выяснить, является ли данная функция аналитической или нет хотя бы в одной точке. 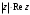 Решение: Имеем z = x + yi. Следовательно, 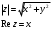 Т.о. 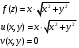 Находим частные производные: 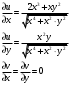 Условия Коши-Римана имеют вид: 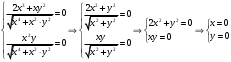 Однако в точке х= 0, у = 0 производная не существует, т.к. знаменатель обращается в 0. Т.о. функция не дифференцируема ни в одной точке и нигде не аналитична. 4. Восстановить аналитическую в окрестности точки 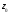 функцию функцию 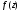 по известной действительной или мнимой части и значению по известной действительной или мнимой части и значению 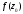 . .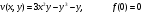 Решение: Находим: 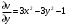 По первому условию Коши-Римана: 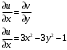 Находим u(x,y): 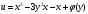 Воспользуемся вторым условием Коши-Римана: 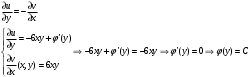 Т.о. 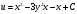 Исходная функция имеет вид: 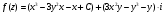 Находим С: 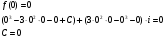 Откуда: 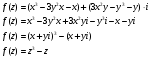 5. Вычислить интеграл от функции комплексного переменного по данной кривой. 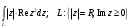 Решение: Кривая L представляет собой честь окружности радиуса R, лежащую в верхней полуплоскости: 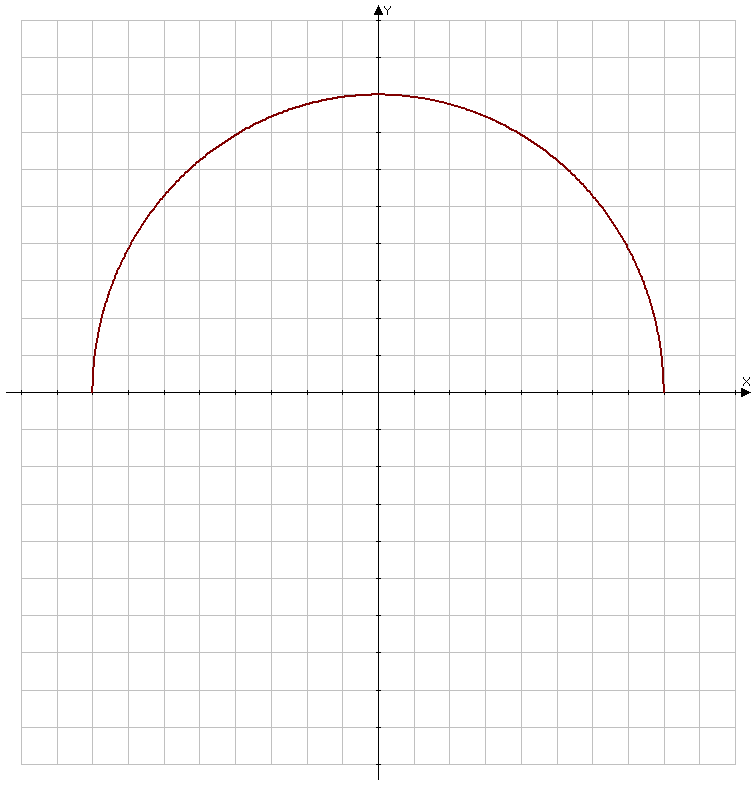 Полуокружность задается параметрическими уравнениями: 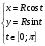 Откуда: 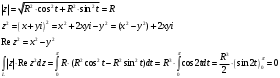 7. Найти все лорановские разложения данной функции по степеням z. 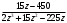 Решение: Найдем точки, в которых знаменатель дроби обращается в 0: 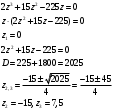 Тогда исходную функцию можно переписать в виде: 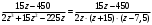 С центром в точке z = 0 можно построить три области, в которых данная функция аналитична: 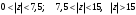 Данная функция является рациональной дробью. Разложим эту дробь на простейшие дроби методом неопределенных коэффициентов: 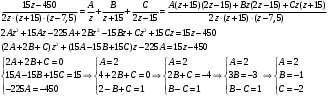 Откуда: 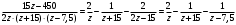 Преобразуем полученные дроби таким образом, чтобы можно было в каждой из областей воспользоваться формулой бесконечно убывающей геометрической прогрессии. При 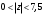 : :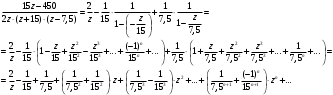 При 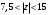 : : При 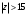 : :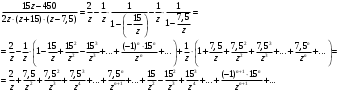 10. Найти изображения данных оригиналов. а) 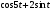 б) 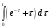 Решение: а) 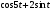 По свойству линейности и пользуясь табличными изображениями получаем: 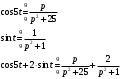 б) 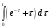 Воспользуемся свойством интегрирования оригинала и свойством линейности: 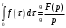 Откуда: 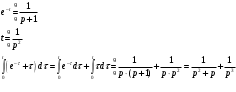 11. Найти оригинал по данному изображению. 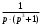 Решение: Разложим исходную функцию на сумму простейших дробей: 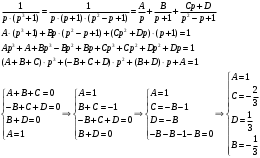 Т.о. 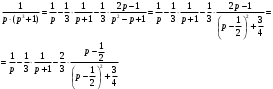 Используя свойство линейности и таблицу изображений, получаем: 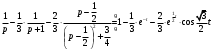 |
