КР 5 Преобразование Лапласа_14. Решение Преобразовываем функцию По таблице изображений и оригиналов получаем
 Скачать 275.73 Kb. Скачать 275.73 Kb.
|
 1. Найти изображение 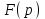 по заданному оригиналу по заданному оригиналу 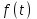 : :Решение: Преобразовываем функцию: 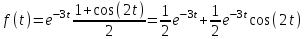 По таблице изображений и оригиналов получаем: 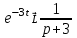 ; ;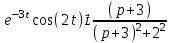 ;; ;;Пользуясь линейностью получаем требуемое изображение: 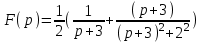 . .Ответ: 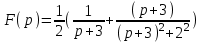 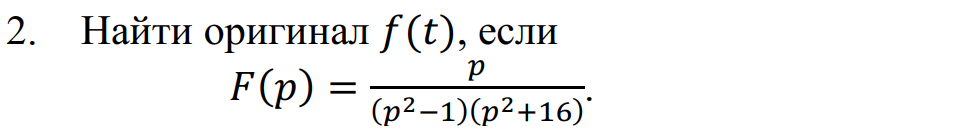 Решение: Раскладываем дробь на простейшие методом неопределенных коэффициентов. 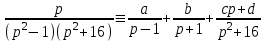 ; ;Умножаем на знаменатель и приводим подобные: 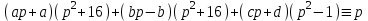 ; ;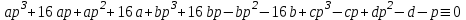 Приравниваем к нулю коэффициенты при каждой степени. 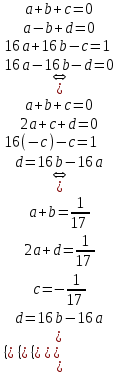 ; ;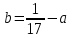 ; ; 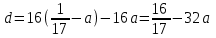 ; подставляем во 2 равенство системы ; подставляем во 2 равенство системы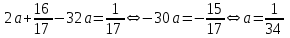 ; ; 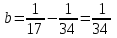 ; ;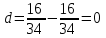 ; получили разложение на простейшие: ; получили разложение на простейшие: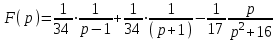 ; ;По таблице изображений и оригиналов получаем: 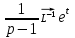 ; ; 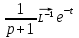 ; ;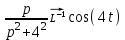 ; ;Пользуясь линейностью обратного преобразования Лапласа, получаем оригинал: 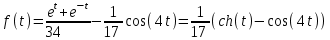 Ответ: 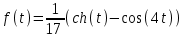 . .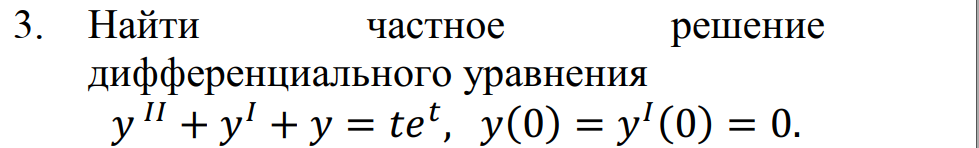 Решение: Находим изображение левой правой части. С учетом данных нам начальных условий. 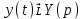 ; ;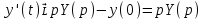 ; ;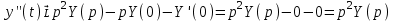 ; ;Теперь ищем изображение правой части. По таблице оригиналов и изображений имеем: 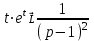 Подставляем в исходное уравнение, получаем операторное уравнение: 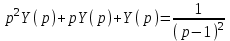 ; выражаем отсюда ; выражаем отсюда 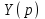 : :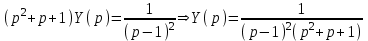 ; ;Осталось восстановить оригинал по полученному изображению. Разложим дробь на простейшие методом неопределенных коэффициентов. 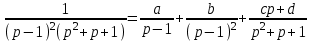 ; ;Умножаем на знаменатели и приводим подобные: 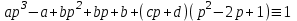 ; ;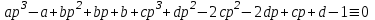 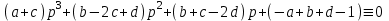 Приравниваем к нулю коэффициенты при каждой степени. 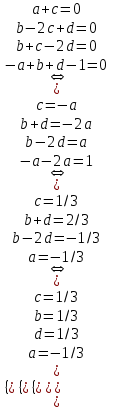 ; ;Получили разложение нашей дроби на простейшие: 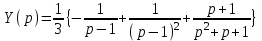 ; восстанавливаем оригинал: ; восстанавливаем оригинал: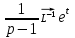 ; ; 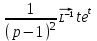 ; последнее слагаемое перепишем в виде: ; последнее слагаемое перепишем в виде: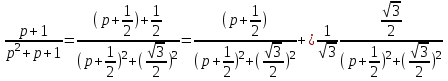 ; ;По таблице изображений и оригиналов получаем: 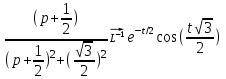 ; ; 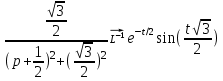 (тут мы еще пользуемся теоремами опережения/запаздывания). По линейности получаем требуемый оригинал 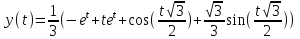 . .Ответ: 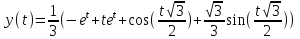 . .(можно честно подставить в уравнение, и проверить, что ответ верный). 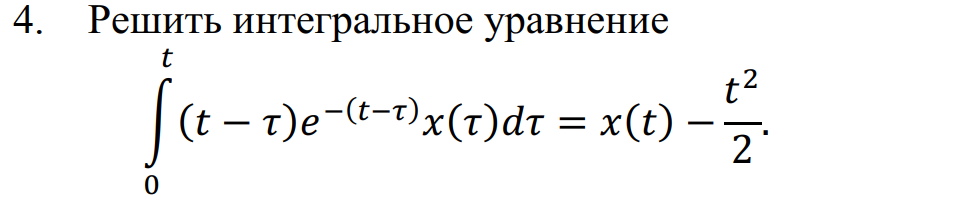 Решение: Слева имеем свертку функций 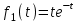 и и 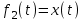 ; находим изображение первой функции ; находим изображение первой функции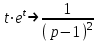 ; ;По теореме о свертке функций (использую таблицу изображений и оригиналов) получим изображение интеграла: 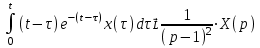 . .Находим изображение правой части. 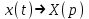 ; ; 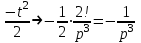 ; ; Подставляем, получаем операторное уравнение: 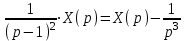 ; выражаем отсюда ; выражаем отсюда 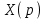 . .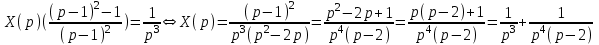 Восстанавливаем оригинал по этому изображению Для этого нужно разложить вторую дробь на простейшие. Делаем это методом неопределенных коэффициентов. 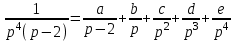 ; умножаем на знаменатели и приводим подобные: ; умножаем на знаменатели и приводим подобные: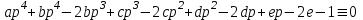 ; ;Приравниваем коэффициенты при каждой степени к нулю 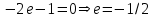 ; ;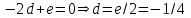 ; ;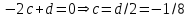 ; ;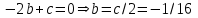 ; ;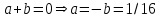 ; ;Получили разложение: 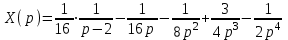 (не забыли, что у нас еще было 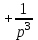 слагаемое). слагаемое).По таблице изображений и оригиналов получаем: 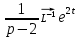 ; ; 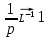 ; ; 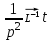 ; ; 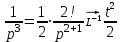 ; ;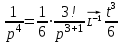 . .В силу линейности получим 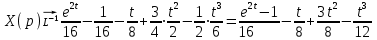 ; ;Ответ: 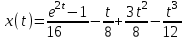 . .  С помощью формулы Дюамеля найти решение уравнения: С помощью формулы Дюамеля найти решение уравнения: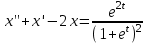 , , 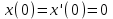 .(1) .(1)Решение: Рассмотрим сперва уравнение с такой же левой частью и правой частью 1 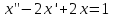 Переходим к изображениям 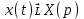 ; ;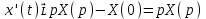 ; ;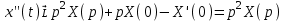 ; ;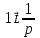 . Получаем операторное уравнение . Получаем операторное уравнение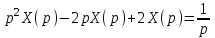 ; ;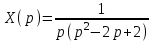 ; ;Раскладываем нашу дробь на простейшие методом неопределенных коэффициентов. 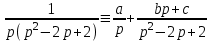 ; умножаем на знаменатели и приводим подобные: ; умножаем на знаменатели и приводим подобные: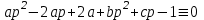 ; ; 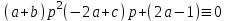 ; значит, все коэффициенты нули ; значит, все коэффициенты нули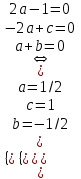 ; получили разложение: ; получили разложение: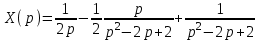 ; ;Надо найти оригинал по этому изображению. 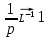 ; ; 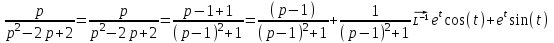 ; ;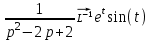 (выше написали, почему). (выше написали, почему).В силу линейности, получаем оригинал (решение уравнения с единицей в правой части) 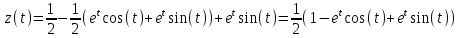 ; ;Находим производную 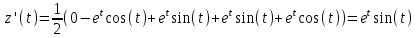 ; ; Правая часть исходного уравнения 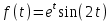 ; ; Согласно формуле Дюамеля, решение исходного уравнения есть 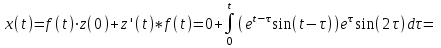 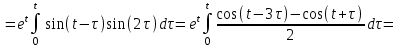 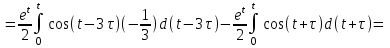 (формула Ньютона-Лейбница) (формула Ньютона-Лейбница)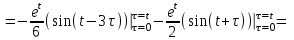 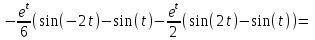 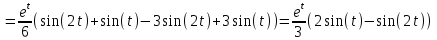 Ответ: 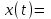 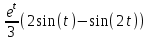 |
